蜘蛛结网结构的讨论与优化
2013-10-22刘家保陈中华
刘家保,陈中华,余 蔓
(1.安徽新华学院公共课教学部,安徽 合肥 230088;2.安徽新华学院商学院,安徽 合肥 230088)
1 问题的基本假设
一个实际问题不经过简化假设就很难翻译成数学问题,即使可能也会很难求解,不同的假设会得到不同的模型,假设过分简单,会导致模型的失败或部分失败,假设过分详细,将使问题过分复杂,可能很难甚至无法继续下一步的工作。在本文中,问题已经初步数学化,因此不需要很多的假设过程。为了方便建立数学模型,认为以下假设是必要而且是合理的:
(1)假设问题中的蜘蛛个体种类和大小均相近相同;
(2)假设蜘蛛们织网的基本方法和网结构相近相同;
(3)假设问题中的蜘蛛个体所处的理想自然环境相近相同,所处的理想自然环境不会有很大的改变,蜘蛛个体在理想自然环境下只考虑织网而不考虑其他环境和生物因素。
2 模型的建立与求解
2.1 数学模型实验数据获取及其处理
在实验室中,称出蜘蛛的重量后 (研究中用100只相同蜘蛛的平均体重作为蜘蛛的体重),将42只蜘蛛 (其中体重小于200mg的27只,体重大于200mg的15只)置于大的纱布笼内,让其自由结网。获取的数据有捕食面的上、下半径 (网垂直线上的半径)和内圈补丝的上、下半径,网上、下半面捕丝的圈数和半径丝的根数,对于具有支持带的网,还收集了各条支持带的长度以及宽度 (取支持带长度四等分点上宽度的平均值)[1]。在收集蛛网数据后,将网收掉,以便蜘蛛在较短的时间内结新网。对每只蜘蛛连续观测3张网,并将每只蜘蛛的3张网视为3个重复,对体重0.15mg的蜘蛛采集两张网的数据。在实验观测期间,仍如上述所述进行喂食。
将网捕食面近似地看成上下两个不同半径的半圆环组合,则有:

使用变异系数来描述各指标(捕丝总长度、捕食面面积和平均捕丝间距)的变化程度:

本研究的数据均采用SPSS 11.0软件进行Pearson相关分析[2-4](双尾假设实验)。
2.2 模型的分析及其结果
2.2.1 不同类型蜘蛛网之间的比较
由实验数据观察可知,蜘蛛的重量对蜘蛛网的结构有不同程度的影响,假设所取蜘蛛的重量相同并且该蜘蛛能结不同类型的正多边形网,为使问题简化只研究网的一环,即一个正多边形 (图1所示),然后进行计算比较,由此假设可以得到以下结果:

图1 正多边形网和圆网数学模型图


其外接圆的周长和面积分别为:
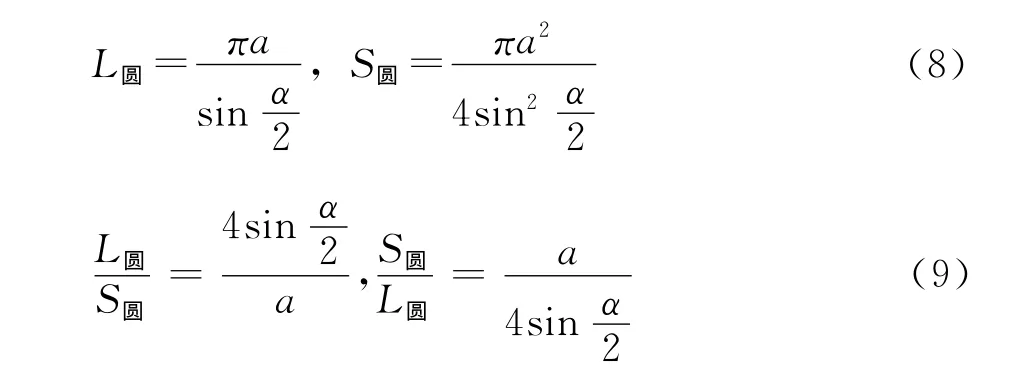

2.2.2 圆形蜘蛛网的最优说明
由Cyclosa mulmeinensis实验[5-7]得出的蜘蛛网几何模型进行分析。
(如图2、图3所示)
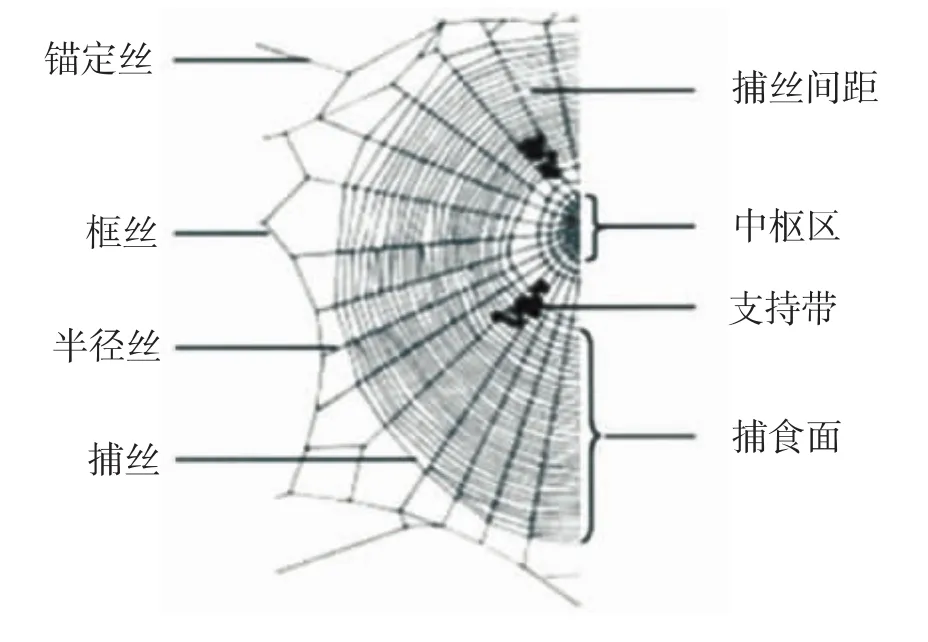
图2 蜘蛛圆网的模式结构

图3 蜘蛛圆网的数学模型图
在实验室中,搜集了大量资料并观察了137只蜘蛛和它们所结的网,并用卡尺和量角器测出蛛网网格尺寸[8](其中网格角度测量线与地面平行),分析数据得到如下公式:

进一步实验,用立体显微镜测出被捕食者的长度,蛛网的捕食数量用一个对数线性模型来比较 (使用R统计软件包统计分析),公式如下:)

2.2.3 圆形蜘蛛网角度对圆形蜘蛛网相关变量的影响
如果将蛛网倾斜与地面成0°(0°,90°分别表示水平和垂直),设立四个组讨论有支持带或没有支持带的效用:没有支持带的水平圆网和有支持带的水平圆网;没有支持带的垂直圆网和有支持带的垂直圆网。
通过蛛网的捕获数据分析得到,倾斜度是主要的影响,支持带的影响可以忽略不计,但它们之间是相互影响的。以上表明不论蛛网水平或垂直放置,有支持带的蛛网面积大小是差不多的,但是没有支持带垂直放置的蛛网面积通常比较大。不论蛛网是怎么放置的,有支持带的蛛网网格比较狭小,但是对于蛛网网格的倾斜度和有无支持带之间没有相互影响的作用。蛛网有偏离度ABW (即蛛网的下部比上部大)[9,10]对捕食是不利的。虽然对于蛛网网格的倾斜度和有无支持带之间没有相互影响的关系,但是有支持带的蛛网比没有支持带的蛛网的偏离度要大。
图4 蛛网的角度与捕获面面积之间的关系

图5 捕获面面积CA,网格宽度MW,偏离度ABW
2.2.4 问题模型的相关结论
由以上问题建立的数学模型可以得到如下主要结论:
(1)当蜘蛛丝的长度一定时,圆网的捕食面面积比正n边形的面积大,所以圆网的捕获概率大于正n边形网;
(2)当捕食面面积相同时,圆网的用料比正n边形网用料要少;
(3)当蜘蛛网的结构是呈垂直放置时,蜘蛛网的结构最优;
(4)蜘蛛网支持带的量要适度 (影响蛛网的大小和偏离度)。
3 模型优缺点及改进方向
3.1 问题模型的优点
(1)本文建立的问题模型是在现实实验的基础上建立而成的,有一定的合理性和真实性;
(2)问题模型中的相关结论探究也都是建立在问题的实际模型基础上,具有一定的科学合理性;
(3)问题建立的数学模型能够比较直观地反映出圆形蜘蛛网各个方面的优化因素及其影响比重,通过问题的数学模型计算提供出的图表能够充分为本文得出的结论提供理论支撑。

图6 改进后的圆形蛛网模型结构
3.2 问题模型的缺点
(1)由于时间、团队研究能力等方面的原因和限制,本文建立的模型仍然比较模糊,并且只是着重建立了圆形蜘蛛网的相关数学模型结构,没有对其他规则或不规则蜘蛛网模型进行相关的研究讨论,导致论文结论比较单调、不全面。
(2)由于实验数据的不足,无法验证所建立模型的准确性。又由于本文实验数据的取材和处理都比较单一,所得出的结论具有比较大的地理、个体等条件的局限性。
3.3 问题模型的改进方向
当蜘蛛丝的长度一定时,改进后的圆网的捕食面面积比上述讨论的圆网的面积更大;当捕食面面积相同时,改进后的圆网的用料比上述讨论的圆网用料更少。从以上的相关结论中可以推导出上述圆形蛛网的更优化数学模型如图6所示。
[1]卓春晖,蒋平,吴灵芝.不同体重悦目金蛛的蛛网结构[J].Chinese Journal Of Zoology,2007,42(02):134-139.
[2]蒋平,肖永红,吕太勇.蜘蛛丝的结构与机械性能研究进展[J].井冈山大学学报:自然科学版,2010,31(04):37-43.
[3]曹政才,韩丁富,乔非.基于新型路网模型的路径寻优方法研究[J].电子学报,2012,4(40):756-761.
[4]Takeshi W.Web tuning of an orb-web spider,Octonoba sybotides,regulates prey-catching behaviour[J].Biol Sci,2000,267:565-569.
[5]Li D,Lee W S.Predator-introduced plasticity in web-building behaviour[J].Anim Behav,2004,67:309-318.
[6]李林.经济系统中几个微分方程模型[J].中国科学院研究生院学报,2003,20(03):273-275.
[7]Heiling A M,Herberstein M E,Spitzer G.Calculation of capture thread length in orb webs.evaluation of new formulae[J].Ann Entomol Soc Am,1998,91:135-138.
[8]刘立嘉,盛业华,路明月.双向半序网在两点间最优路径算法中的应用[J].计算机工程,2008,34(07):73-75.
[9]Herberstein M E,Tso I M.Evaluation of formulae to estimate the capture area and mesh height of orb webs[J].Arachnol,2000,28:180-184.
[10]Schneider J M,Vollrath F.The effect of prey type on the geometry of the capture web of Araneus diadematus[J].1998,85:391-394.
