基于分段幂函数的LMD方法及其在轴承故障诊断中的应用

肖 露，熊邦书，莫 燕，赵平均

(1.无损检测技术教育部重点实验室(南昌航空大学)，南昌 330063;2.中航工业洪都航空工业集团有限责任公司飞机设计研究所，南昌 330024）

0 引言

滚动轴承是旋转机械中最重要的零部件之一，在运行过程中，若出现故障，则会造成严重后果;因此，滚动轴承的故障诊断对保障旋转机械安全工作具有重要意义。

由于滚动轴承在工作过程中受载荷、摩擦以及噪声等因素影响，实际采集到的振动信号是一种非平稳的多分量调幅—调频信号，因此时频分析方法是目前滚动轴承故障诊断的主流方法。现有时频分析方法可分为3类，第1类为线性时频变换，如Potter等首次提出了通过滑动时窗来计算频谱的短时傅里叶变换［1］，Morlet提出了基于时间－尺度的小波分析［2］等，这类方法受到测不准原理的约束，并缺少自适应性［3］。第2类为非线性时频变换，起源于量子力学的 Wigner分布［4］，因其良好的时频聚集性无需加窗，得到了广泛应用［5］。第3类为自适应时频分析方法，其中最经典的方法有Huang提出的经验模式分解(Empirical Mode Decomposition，EMD)［6］，该方法先将信号分解为各个本征模态函数，再进行Hilbert分解，可得到清晰的时频分布;2005年Smith提出局域均值分解(Local Mean Decomposition，LMD)［7］，LMD将非平稳多分量信号分解为一系列瞬时频率有物理意义的PF(Production Function)和一个残余分量之和，每个PF为单分量信号，结合所有PF可得到整个信号的时频分布［8］，该方法改善了EMD的端点效应，避免了EMD中的无意义负频率，是时频分析领域的重要突破。

传统LMD采用滑动平均计算局域均值函数与局域包络函数，若滑动跨度选取不当会引起函数不收敛［9］，且导致过平滑，影响算法精确度;因此，本研究提出一种改进算法，采用分段幂函数法分别求取信号极大值点集和极小值点集的包络线，上下包络线之和的均值为局域均值函数，上下包络线之差绝对值的均值为局域包络函数，避免过平滑现象，得到的局域包络与局域均值函数更精确，并通过仿真信号分析及其在滚动轴承故障诊断的应用，以验证所设计方法的有效性。

1 LMD算法原理

LMD将多分量的非平稳信号分解为若干个单分量的PF和一残余分量。每个PF由一个包络信号和一个纯调频信号相乘组成。PF的瞬时幅值由包络信号得到，瞬时频率由纯调频信号得到。具体方法如下:

Step 1:根据找出的信号x(t)的极值点集n(i)，求出第i段的局域均值点m(i)和包络估计点a(i)，如式(1)和式(2)所示:

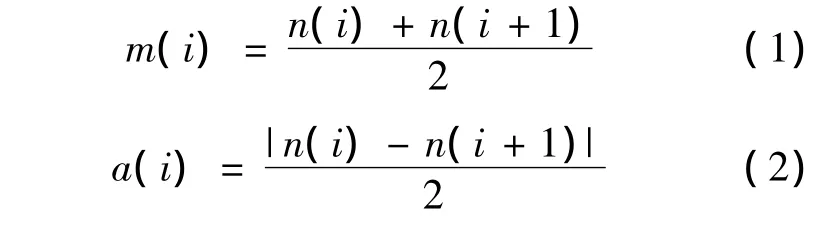
Step 2:分别对局域均值点和包络估计点滑动平均处理得到局部均值函数m11(t)与局域包络函数a11(t)，滑动平均计算公式为

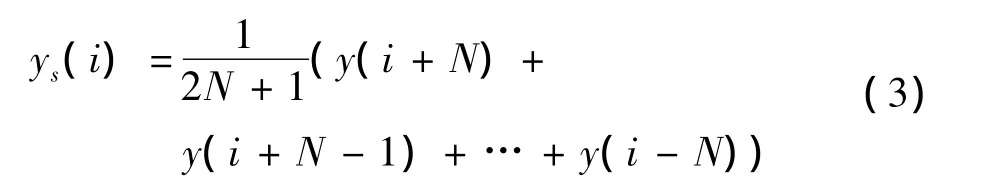
Step 3:从信号x(t)中分离出局域均值函数m11(t)，得

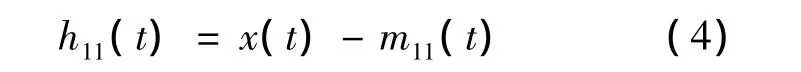
Step 4:已剔除均值的信号h11(t)除以包络信号，得

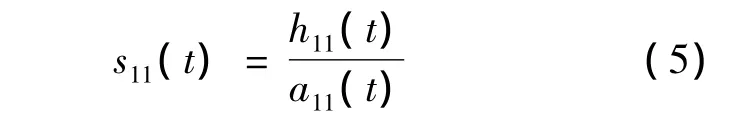
Step 5:若新信号s11(t)对应的局域包络函数a12(t)=1，则其为符合要求的纯调频信号;若不为纯调频信号，则重复3，4步的迭代，直至其为纯调频信号s1n(t)，这里

Step 6:由迭代结果得到PF1分量

其中:s1n(t)为纯调频信号，可表示PF分量的瞬时频率;a1(t)可表示为PF分量的瞬时幅值，表达式为

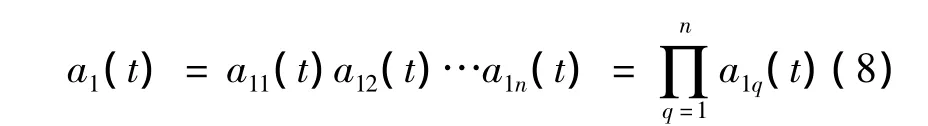
Step 7:分离出原始信号x(t)中的PF1(t)，得到u1(t)，将u1(t)作为原始信号重复前六步直至uk(t)的极点数不大于1，分离出所有PF分量。x(t)的最终表达式为

LMD分离出若干个PF，能够完全表示整个信号的时频特性，并用于多分量信号的分析和特征提取。

2 基于分段幂函数的LMD算法

LMD算法通过找到所有极值点集，应用滑动平均法求取局域均值函数与局域包络函数。滑动平均法会引起过平滑，且普遍选择最大局域均值的1/3为滑动平均跨度，易造成冲击类信号处理失真。针对上述问题提出一种分别找出信号的极大极小值点集，用分段幂函数求取包络线以得到局域均值函数和局域包络函数的算法。

2.1 分段幂函数方法原理

分段幂函数插值方法原理为:设有插值点P1，P2，P3，首先连接 P1，P3，过 P2作平行于 P1P3的直线，该直线与x=x1和x=x3分别相交于A，B点(图1)。以为x轴，点P2为原点建立新的坐标系，则点A在新坐标中映射为x轴上坐标为(x1－x2，0)的点A'，点B在新坐标中映射为 x轴上坐标为(x3－x2，0)的点B'。取与x轴垂直的向量得到点P1在新坐标中的映射点，取得到点P2在新坐标中的映射点(图2)。在图2中作幂函数曲线y=xβ(β＞1)，同分别位于x轴左右两侧的与相交于C，D 点。

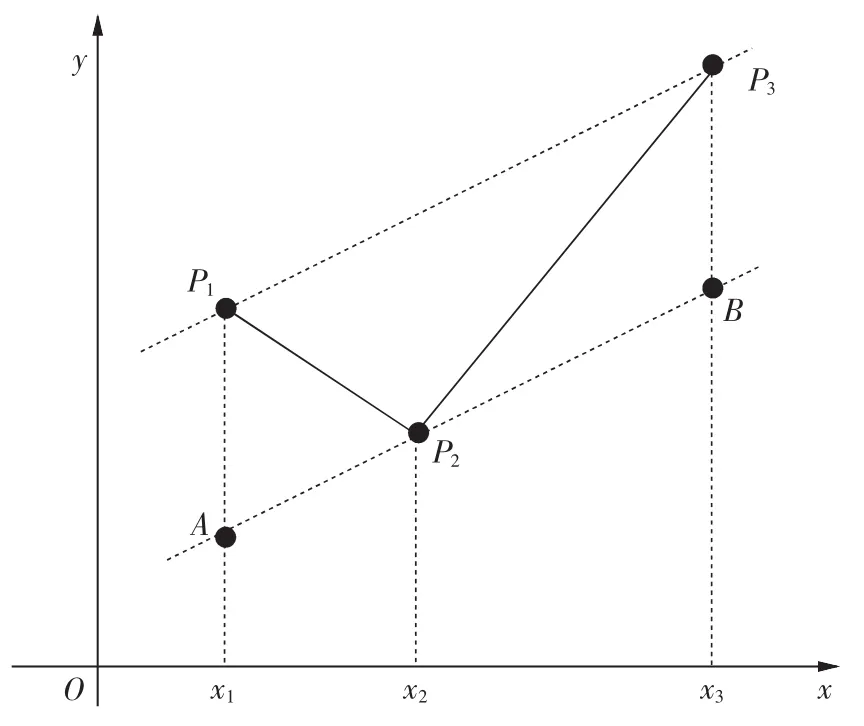
图1 分段幂函数算法中A，B的含义Fig.1 The meaning of A and B in piecewise power function algorithm

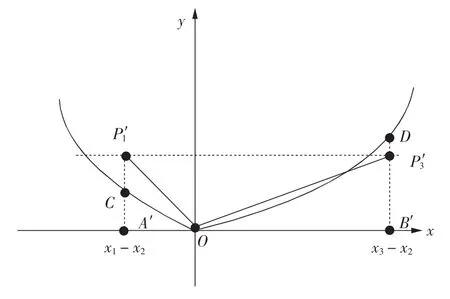
图2 分段幂函数算法中C，D的含义Fig.2 The meaning of C and D in piecewise power function algorithm

则由此构建函数［9］:

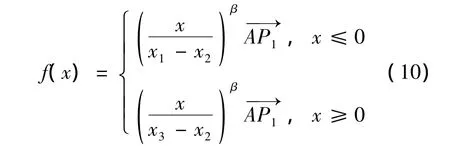
其中，

设过点P2与P1P3平行的直线为g(x)，插值公式为

则过点 P1，P2，P3的曲线为

同理，P2，P3，P4的插值结果为 s2(x)，则 P2，P3之间的曲线为

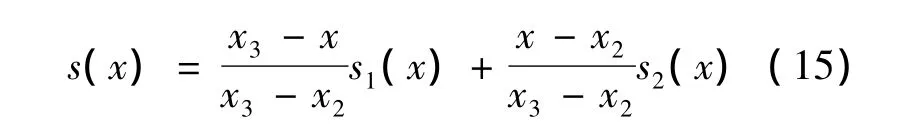
因此可得，对于点集 Pi(i=1，2，…，n)，将Pi－1，Pi，Pi+1分段幂函数插值得到 si(x)，Pi，Pi+1，Pi+2插值得到 si+1(x)，则依照式(15)得 Pi与Pi+1之间最终的曲线表达形式s(x)。函数s(x)在定义域范围内一阶连续可导，即曲线s(x)为单值光滑曲线。文献［10］证明了分段幂函数误差与β成反比，误差范围比3次样条插值等要小，说明该方法适合于非平稳非线性振动信号的包络生成。

2.2 基于分段幂函数的LMD算法过程

基于分段幂函数的LMD算法与传统LMD算法在求取局域均值函数和局域包络函数上不同，其他步骤相同。计算局域均值和局域包络函数的主要步骤如下:

Step 1:分别计算振动信号的极大值点集maxi(i=1，2，3，…，M)和极小值点集 mini(i=0，1，2，3，…，N)。

Step 2:采用分段幂函数法，即利用式(12)和式(15)对极大值点集拟合得到包络线Emax(t)，对极小值点集拟合得到包络线Emin(t)。

Step 3:由包络线Emax(t)和Emin(t)得到局域均值函数m(t)和局域包络函数a(t)，其计算公式为

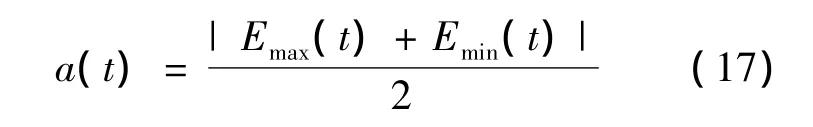
与传统LMD相比，本算法不需重复计算，且其误差界较小，故在计算效率和精确度上有较大的优势。

3 仿真信号分析

为了验证本改进LMD算法的性能，采用一个非线性信号进行仿真实验，其表达式为

仿真信号由3个分量相加而成，其中:x1为调频调幅信号，基频为100 Hz，调制频率为5 Hz;x2为纯调频信号，基频为30 Hz，调制频率为7.5 Hz;x3为频率为7 Hz的正弦信号。信号x及3个分量x1，x2，x3的波形图如图3所示。

图3 各组成分量的仿真信号Fig.3 The simulation signals of all components

图4、图5分别给出了采用传统LMD算法和改进算法对仿真信号的分解结果。可以看出:图4中传统LMD分解的残余分量Res起伏较大，而图5中残余分量Res比较平缓，无明显波动极值点，残余分量值较小。为了量化评估2种算法的性能，分解信号的相关系数、均方误差(Mean Squared Error，MSE)如表1所示，从表1可以看出:1)改进算法分解的3个PF分量的均方误差明显小于传统LMD方法，其分解精度更高，分解更接近于理想结果;2)改进算法所得Res的相关系数小于0.1，为伪分量，可不予考虑，且Res的相关系数的值小于传统LMD，说明改进算法分解得更彻底。计算2种算法运行时间，传统LMD算法为3.36 s，改进算法为3.08 s，节省了运算时间。

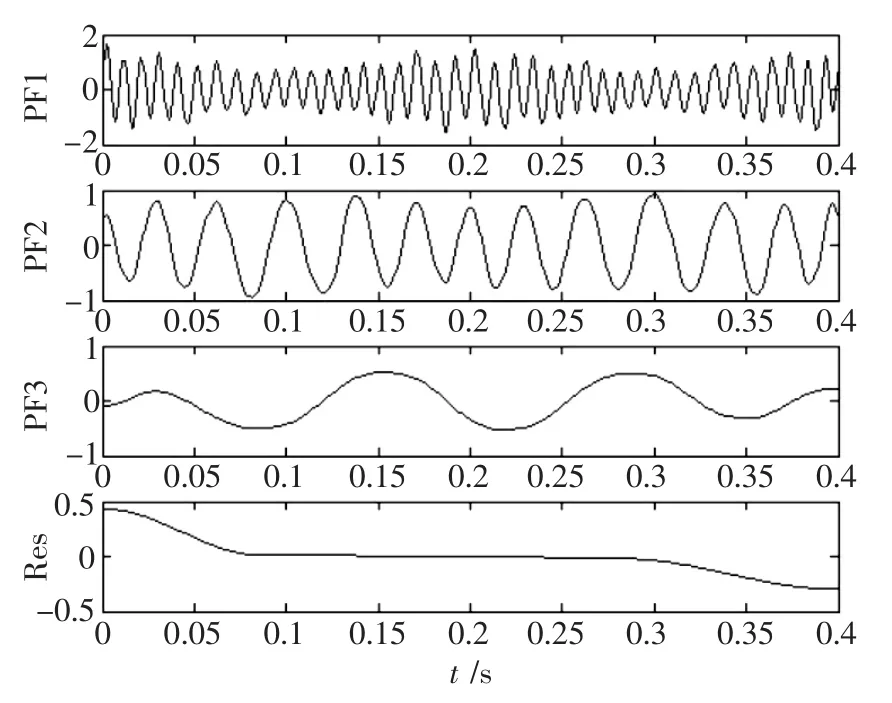
图4 传统LMD算法分解结果Fig.4 The decomposition result of the traditional LMD algorithm

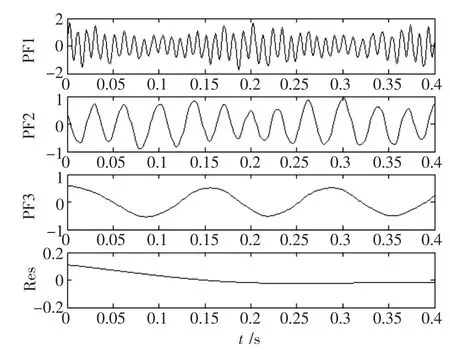
图5 改进算法的分解结果Fig.5 The decomposition result of the improved algorithm

表1 两种算法性能对比Table 1 Performance comparison of two kinds of algorithm

4 滚动轴承故障诊断实验

本研究采用美国凯斯西大学电气工程与计算机科学系轴承实验数据［11］进行实验，测试轴承为6502—2RS SKF深沟球，其钢球直径d=8 mm，球组节圆直径D=40 mm，钢球数N=9，接触角α=0°。数据的采样频率为12 kHz，采样点N=1024，发动机转速n=1797 rpm/min，旋转频率fr=n/60。

图6、图7分别给出了信号经传统LMD算法和改进算法分解的结果，可见:传统LMD经过4次分解才能得到平缓的残余分量Res，PF4及残余分量Res与原信号相关系数分别为0.028 0和0.0241，远小于0.1，为不含有效信息的伪分量，可剔除，但根据Res单调的终止条件仍需继续分解，分解效率低;改进算法只需进行3次分解就可得到有效分量以及符合要求的残余分量Res，分解效率高。

图6 传统LMD算法实例信号分解结果Fig.6 The instance signal decomposition result of the traditional LMD algorithm

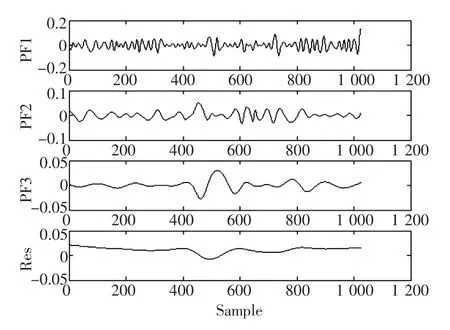
图7 改进算法实例信号分解结果Fig.7 The instance signal decomposition result of the improved algorithm

将本研究设计的改进算法应用于轴承故障诊断。由于损伤轴承零部件会周期碰撞损伤位置，形成具有不同通过频率的减幅振荡，可以此作为判别不同故障的依据。采用滚珠故障数据，依据式(19)结合上述的实验滚动轴承参数可得滚珠故障频率 fd=141.17 Hz。

分别对改进算法的各PF分量进行分析。根据计算PF3与残余分量的相关系数均小于0.1，为伪分量，可不予考虑。PF1和PF2频谱图分别如图8a、8b所示:

图8 故障诊断频谱图Fig.8 The spectrum diagram of fault diagnosis

图8中PF2分量在140.8 Hz处存在明显的谱线，与式(19)的理论故障频率结果相近，可确定为故障频率;在 PF1 分量的 58.59、117.2、210.9 Hz及PF2分量94.19 Hz处存在明显谱线，分别与轴承基频的2倍频59.9 Hz、4倍频119.8 Hz、7 倍频209.65 Hz及3 倍频89.85 Hz接近，与信号存在基频倍频这一实际相符，由此可以判定轴承出现了以140.8 Hz为特征频率的滚珠故障。上述实验验证了本研究所设计的算法可应用于滚动轴承故障诊断。

5 结论

1)本研究提出了一种基于分段幂函数法的LMD改进算法;

2)将改进算法分别采用信号上下极值点包络线计算LMD中局域均值函数与局域包络函数，避免了传统LMD算法的过平滑，分解结果更精确，运算时间缩短;

3)通过仿真信号分析和轴承故障诊断实验，验证了方法的优越性和有效性。

［1］Auslander L，Buffalano C，Orr R S，et al.Comparison of the Gabor and short-time Fourier transforms for signal detection and feature extraction in noisy environment［J］.Proceedings of the International Society for Optical Engineering，1990，1348:230－247.

［2］罗光坤.Morlet小波变换理论与应用研究及软件实现［D］.南京:南京航空航天大学，2007:13－23.

［3］孙云岭，朴甲哲，张永祥.Wigner-Ville时频分布在内燃机故障诊断中的应用［J］.振动与冲击，2004，15(6):505 －507.

［4］马辉，赵鑫，赵群超，等.时频分析在旋转机械故障诊断中的应用［J］.振动与冲击，2007，26(3):61－64.

［5］向玲，唐基贵，胡爱军.旋转机械非平稳振动信号的时频分析比较［J］.振动与冲击，2010，29(2):42－46.

［6］Huang N E，Zheng S，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London，1998，454(1971):903 －995.

［7］Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005，2(5):443 －454.

［8］任千达.基于局域均值分解的旋转机械故障特征提取方法及系统研究［D］.浙江:浙江大学，2008:60－65.

［9］钟佑明，金涛，秦树人.希尔伯特－黄变换中的一种新包络线算法［J］.数据采集与处理，2005，20(1):13－17.

［10］刘霖雯，刘超，江成顺.EMD新算法及其应用［J］.系统仿真学报，2007，19(2):446 －448.

［11］Case Western Reserve University Bearing Data Center Website.Bearing Date Center Seeded Fault Test Date［DB/OL］.［2011 －05 －03］.http://www.eecs.case.edu/laboratory/bearing/.