基于改进ABC与LS-SVM算法的电力负荷预测的研究

李文江，陈 阳

（辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105）

0 引 言

电力负荷预测就是根据预测的需求，釆用一种数学方法，系统地处理过去的历史数据，以实现对未来某特定时段的负荷数值进行高精度的预测。对于发、输电企业，需要依据预测来保证系统运行的安全性和经济性，高精度电力负荷的预测，可以提高电力企业的竞争能力和经济效益［1］。近些年来，许多学者对这一问题进行研究，各种预测方法层出不穷。总结起来说主要分为两类:传统预测方法和人工智能方法。由于科技的发展，传统预测方法不能满足现在的预测要求，因此，人工智能方法成为了现今主要的预测方法。例如人工神经网络方法、小波分析算法、遗传算法等。

本文将人工蜂群（artificial bee colony，ABC）算法［2～4］进行改进并与最小二乘支持向量机（least squares support vector machine，LS-SVM）结合，利用混沌序列蜂群算法优化其训练参数，得到了优化的基于混沌蜂群的LS-SVM的电力负荷预测模型。实验结果表明，基于混沌人工蜂群（CABC）算法的LS-SVM模型的预测精度更高、误差更小，可以更有效地对电力负荷进行预测。

1 算法的基本原理

1．1 CABC算法的基本原理

电力负荷的预测是很多确定的和不确定的因素相互影响共同作用的结果，其序列属于混沌时间序列，必须将电力负荷与混沌理论结合起来，应用先进的机器学习算法，将电力负荷看作这个混沌系统策动的结果和表现，并把混沌动力学的方法用于电力负荷的预测中，以期提高预测的准确率。

又由于ABC算法在目标函数存在多个局部最优解或全优解周围存在谷圈时性能很不理想，容易导致群体多样性的下降，算法过早收敛。此外，考虑到蜂群的趋同性，搜索后期算法不能有效地跳出局部最优解［5］。

混沌具有随机性、遍历性及规律性等特点，在一定范围内能按其自身的规律不重复地遍历所有状态。为此，本文引入禁忌表和混沌搜索对ABC算法进行了改进，利用混沌搜索的遍历性跳出ABC算法的局部最优解。混沌搜索主要步骤如下:

1）产生一个D维的随机初始向量 X0=m0，1，m0，2，…，m0，D。其中，m0，k∈（0，1），并且各个值之间的差异较小。

2）在初始向量X0的基础上，使用Logistic方程（1）产生混沌序列 X0，X1，X2，…，XN。其中

式中 μ为控制变量，当μ=4时，为完全遍历状态。

3）采蜜蜂利用混沌序列，得到新的解

式中i是解的编号，j∈{1，2，…，D}，k∈{1，2，…，N}是随机产生的，且k≠i。如果新解得适应度值比旧解的适应度值大，则记下更新旧解;否则，在旧解的更新失败次数加1。

4）若达到最大迭代次数，则优化过程结束;否则，返回步骤（2）

本文将混沌搜索引入观察蜂的区域搜索中来降低陷入局部极小点的几率。通过和其他优化算法对测试函数优化的效果对比发现，CABC算法优化效果较好。

1．2 LS-SVM的基本原理

SVM［6］的基本思想是基于Mercer核展开定理，通过非线性映射，将输入空间的样本映射到高维的特征空间中，将寻找最优线性回归超平面的算法归结为求解约束条件下的二次规划问题，并可以求得全局最优解。

LS-SVM［7，8］是一种回归预测算法，是标准 SVM 的一种扩展，优化指标采用平方项，并用等式约束代替标准SVM的不等式约束，即将二次规划问题转化为线性方程组求解，降低了计算复杂度，加快了求解速度。LS-SVM方法采用如下形式的函数对未知函数进行估计

式中 w为超平面的权值矢量;b为偏置常数;非线性函数φ（·）将输入空间映射为高维特征空间。

给定训练样本集，LS-SVM定义如下优化问题

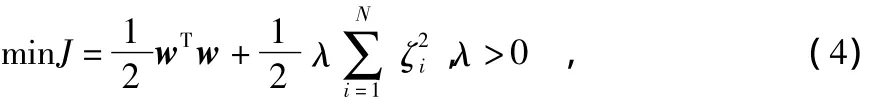
式中 λ为正规化参数。

约束条件为

通过其对偶形式可以求它的最优解

式中 αi为拉格朗日乘子。

对偶形式可以根据目标函数和约束条件建立拉格朗日函数。

根据KKT优化条件有

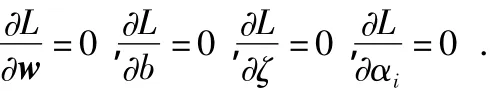
可得

利用核函数的方法，令

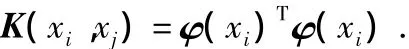
其中，K（xi，xj）为满足Mercer条件的对称函数，根据式

优化问题转化为求解线性方程

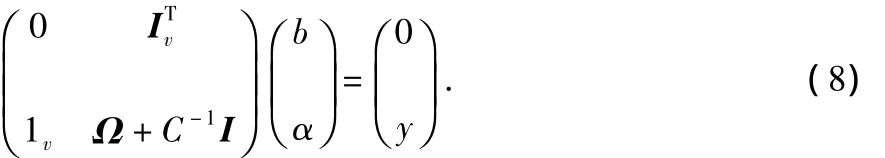
其中

则回归函数为

本文选取RBF核函数来构造LS-SVM，这样需要优化的参数最少，只有正规化参数λ和宽度参数σ。

RBF核函数为

2 CABC-LSSVM算法模型

利用CABC算法对LS-SVM的惩罚因子C和核参数σ进行优化，CABC算法优化LS-SVM的算法流程如图1，建模具体步骤如下:

1）初始化CABC算法中的控制参数。包括蜂群的大小2N，采蜜蜂的数量N=100，观察蜂的数量N=100，解的个数N=100，极限值limit=100，最大循环次数MCN=120以及D维初始量 X0=x0，1，x0，2，…，x0，D。其中，x0，k∈（0，1），并且各个值之间的差异较小。

2）在初始向量X0的基础上，使用方程式（1）产生混沌序列 X0，X1，X2，…，XN。μ 为控制变量，当 μ =4 时，为完全遍历状态。

3）设置CABC算法中适应度函数，并计算每个解得适应度值。

4）采蜜蜂利用混沌序列，得到新的解式（2）。

如果新解的适应度值比旧解的适应度值大，则记下更新旧解;否则，在旧解的更新失败次数加1。

5）计算各解的可能值Pi

式中f（Xi）是第i个解的适合度值。观察蜂根据这些可能值从现有解的邻域中搜索新的解。

6）如果解Xi的更新失败次数超过了预先设定的极限值，那么就说明这个解不能再被优化了，须将它舍弃，用下式产生的新解将其代替

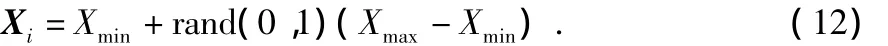
保存最优的解。

7）如果迭代次数大于最大循环次数MCN，则训练结束;否则，返回第4步。

8）将得到的最优解变换成LS-SVM的正规化参数λ和宽度参数σ，并用数据仿真和测试。

3 仿真实验与分析

采用本文所讲预测方法和某地区电网在2012年5月的电量负荷进行预测。选择5月份前28 d的电量负荷及其相关数据作为训练样本，后3 d的数据作为测试样本，对电网的负荷进行预测。本文设定惩罚因子C∈［0．1，150］，核参数 σ∈［0．1，10］，食物源的数量为 20，最大迭代次数为100。采用Matlab仿真平台进行预测，得到的结果如图2。

图1 CABC-LSSVM算法流程图Fig 1 Flow chart of CABC-LSSVM algorithm

图2 实际负荷与预测负荷曲线图Fig 2 Curve of actual load and prediction load

由图2可以看出:预测曲线与实际数据曲线轨迹偏差不大，因此，改进的ABC与LS-SVM算法具有很好的预测精度。通常用平均相对误差的大小来衡量预测的性能，其计算公式为型实际可行，并且具有较高的预测精度和更好的泛化能力。

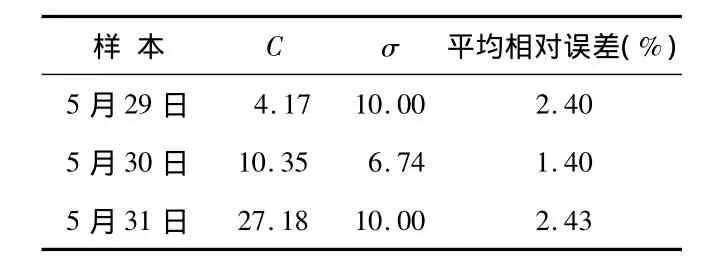
表1 平均相对误差表Tab 1 Table of average relative error

从表1中可以得出:最大误差为2．43%，最小误差为1．4%，平均误差为2．08%。由此可以得出:本文的预测模

4 结束语

在电力负荷的预测中，惩罚因数C和核参数σ对预测结果有重大影响。本文采用改进的ABC算法对这2个参数进行优化，取得最优的解赋给LS-SVM算法进而预测，避免了选取参数的盲目性。通过算法模型的建立和仿真结果的证明:本文所讲方法是可行的，通过此方法可以提高预测的精度，减小误差，对电力负荷的预测有实际意义。

［1］ 霍 明．短期负荷预测的支持向量机模型参数优化方法研究［D］．长沙:湖南大学，2009．

［2］ Karaboga D．An idea based on honey bee swarm for numerical optimization［R］．Erciyes，Erciyes University，2005．

［3］ Karaboga D，Basturk B．A powerful and efficient algorithm for numerical function optimization:Artificial bee colony（ABC）algorithm［J］．Journal of Global Optimization，2007，39（3）:459 －471．

［4］ Karaboga D，Basturk B．A comparative study of artificial bee colony algorithm［J］．Applied Mathematics and Computation，2009，214（1）:108－132．

［5］ 康 飞，李俊杰．改进人工蜂群算法及其在反演分析中的应用［J］．水电能源科学，2009，27（1）:126 －129．

［6］ Cristianini N，Taylo J S．支持向量机导论［M］．英文版．北京:机械工业出版社，2005:93－160．

［7］ Jak S，Vandewalle J．Least squares support machine classifiers［J］．Neural Processing Letters，1999，9（3）:293 －300．

［8］ Gencoglu M T，Uyar M．Prediction of flashover voltage of insulators using least squares support vector machines［J］．Expert Systems with Applications，2009，36:10789 －10798．

［9］ 康重庆，夏 清，刘 梅．电力系统负荷预测［M］．北京:中国电力出版社，2007:12，170．

［10］龚灯才．基于支持向量机的电力短期负荷预测研究［D］．南京:河海大学，2006:50 －51．

［11］李云飞，黄彦全，蒋功连．基于支持向量机的短期负荷预测的方法改进［J］．西华大学学报，2007，26（2）:21 －24．

［12］耿 艳．基于最小二乘支持向量机的短期负荷预测方法及应用研究［D］．济南:山东大学，2008:26－28．