双晶悬臂梁式压电换能器建模与结构参数分析

朱 波，刘文波

（南京航空航天大学自动化学院，江苏南京 210016）

0 引言

无线传感器网络节点一般可能处在野外恶劣环境中，不便更换电池，因此，人们正在寻找一种长期有效的能量采集技术来保证传感器的电源需求，实现长期有效的供电，从而延长无线传感器的使用寿命。环境中振动是普遍存在的，收集环境振动能量为消耗电量低的网络传感器等微机电系统提供一种长久的能源，并有可能取代电池。此项研究越来越受到广泛重视［1～3］。压电晶体属于非中心对称点群晶体，机械载荷作用导致其内部晶胞正负电荷中心产生偏移从而引发极化，这就是正压电效应;反之，如果晶体在外加电场激励下集体在某个方向产生变形叫做逆压电效应。因此，压电材料可以作为将机械振动转换为电能的元件，以实现采集能量为无线传感器供电的目的。但是，压电材料自身很脆，谐振频率高，电源特性很差（高电压、低电流、高阻抗），尤其在低频情况下表现得更加明显，而环境中大多数振动源的频率在400 Hz以下，即属于低频范围。这严重限制了压电换能器的发展和应用。通过将压电材料和金属材料结合形成悬臂梁结构，并在末端附上质量块以降低谐振频率，能较好地解决这个矛盾。目前主要采用双晶悬臂梁式的结构，实现从振动源获取能量的目的。为进一步提高悬臂梁的发电效率，建立系统压电模型与参数优化分析的方法是压电结构设计的关键技术问题。本文针对如何实现结构设计中参数优化问题，通过建立机电耦合的等效电路模型得到了输出功率和谐振频率的计算公式，输出功率随参数变化的曲线。分析了一些参数对输出功率的影响，提出了一些新的结论，为悬臂梁是压电换能器的设计提供了理论依据。

1 压电双晶换能器建模

通过对压电悬臂梁进行受力分析，得到一个等效电路模型。从而求出悬臂梁的谐振频率计算公式和在一定加速度和频率的振动激励下输出电压和功率的表达式。

1．1 换能器构成

如图1所示为一典型的压电双晶悬臂梁结构，金属层的上面表面都贴有压电陶瓷，固定端固定于基座中，梁的自由端附有质量块［4］。当基座上下运动时，梁的自由端在惯性的作用下也上下运动，悬臂梁将发生弯曲变形，压电材料的两表面间产生电压。从而将机械的振动转换为电能。

图1 换能器结构图Fig 1 Structure diagram of energy converter

1．2 应力应变分析

1．2．1 外力对压电层中应力的影响

根据材料力学，EpIp+EcIc=EpIj，所以，复合梁模型的惯性矩可等效为［5］

压电陶瓷上平均应力

梁弯矩

联立式（2），式（3）得

式（4）描述了压电陶瓷平均应力和z方向上外力间的关系，用常数k1来描述

1．2．2 梁自由端扰度和压电层应变间关系

根据Ruler标准梁方程可知弯曲梁曲率表达式为

又由梁的应力和应变间关系有

σ=Epδ（其中δ为应变）．（7）

联立式（3），式（6），式（7）得到悬臂梁自由端扰度和压电层应变之间的关系

令

1．3 等效模型的建立

1．3．1 悬臂梁整体受力分析

将整个悬臂梁系统看做一个质量—弹簧—阻尼系统进行受力分析可得

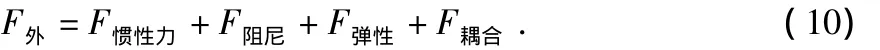
将式（10）乘以k1得

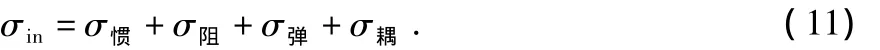
而

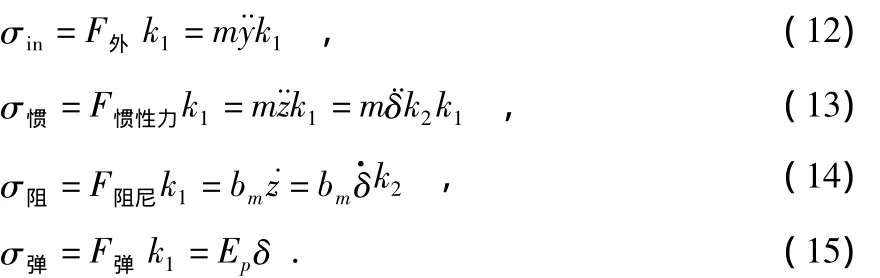
其中，σ藉为可用于进行机电耦合的应力。

1．3．2 机电耦合中应力和输出电压关系

由第一类压电方程［6］

令S=0得

压电陶瓷片产生的电压和电场关系［7］

联立式（17），式（16）得到用于机电耦合的应力和输出电压间关系

其中，a=1表示双晶串联，a=2表示双晶并联。

压电双晶片的等效电容

其中，a=1表示双晶串联，a=2表示双晶并联［8］。

1．3．3 系统电学模型建立

将应力类比为电压，应变的微分类比为电流。根据式（11），式（12），式（13），式（14）可将整个系统等效如图2所示。

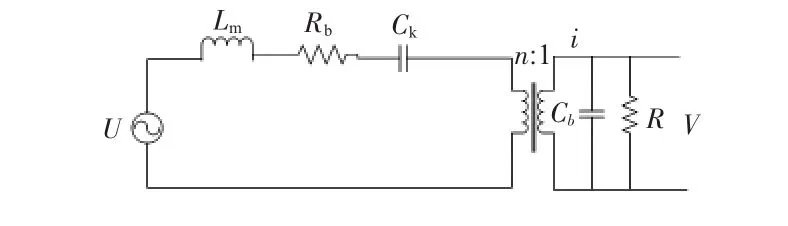
图2 等效模型图Fig 2 Equivalent model chart

由式（12）得

由式（13）得

由式（14）得

由式（15）得

由式（18）得

1．4 系统求解

1．4．1 谐振频率求解

当不带负载时，即R=0。由图2可得

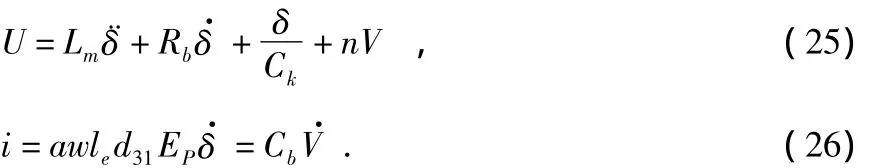
联立式（25），式（26），并进行拉氏变换得

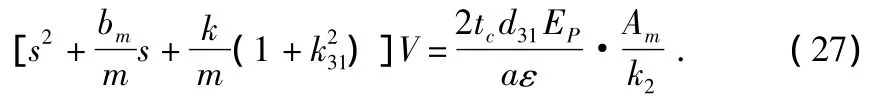
其中，Am为基座的加速度。

由式（27）得谐振角频率

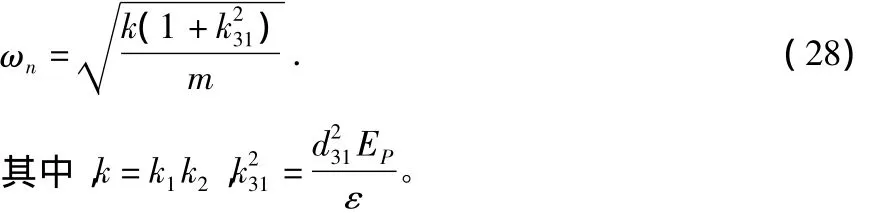
由式（28）可知，增加质量块的重量将减小谐振频率。

1．4．2 输出电压与功率求解

为了计算输出功率和最优负载，假设接上负载用电阻R表示，则有

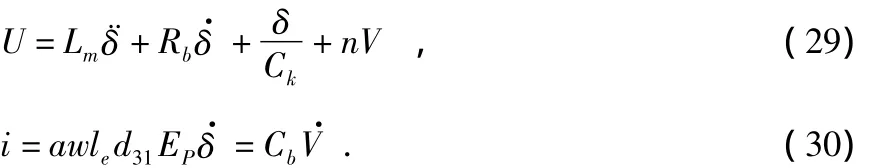
联立式（29），式（30）可以解得在频域范围内的电压输出

2 仿真分析

将压电陶瓷PZT—5的材料参数、悬臂结构参数等代入式（31），式（32）中，并利用Matlab计算得到仿真图如图3～图6。

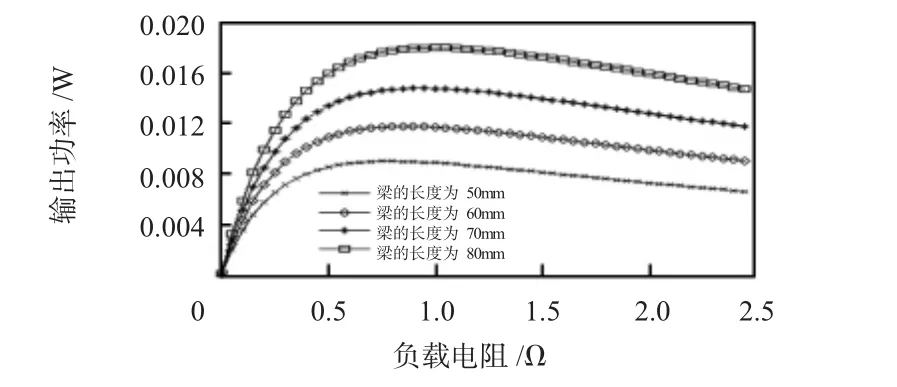
图3 功率随负载变化Fig 3 Power change with load

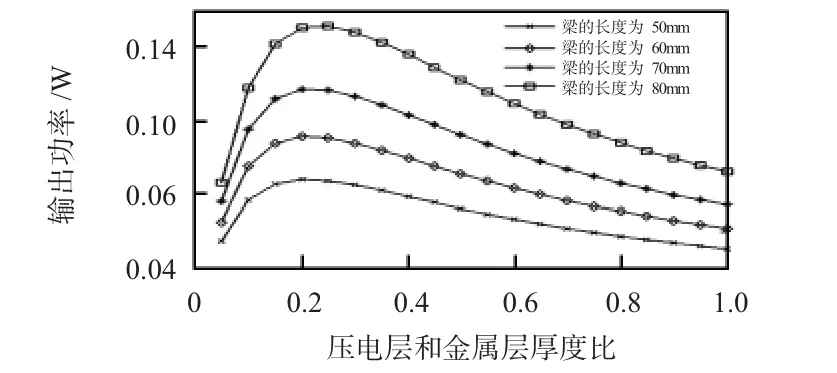
图4 功率随厚度比变化Fig 4 Power change with thickness ratio

由图3可以看出:输出功率先随负载的增大而增大，然后随着负载的增大而减小，亦即存在一个使得输出功率最大的负载值。从图4可以看出:逐渐增大压电层和金属层厚度的比值，输出功率先增大后减小。通过图5可以看出:当电极和梁的长度比大约在0．8左右时，输出功率达到最大。图6表明:当质量块的质量从5 g逐渐增加到13 g时，谐振频率降低，输出功率增大。增加质量块的重量不仅能降低谐振频率也能提高能量转换效率。

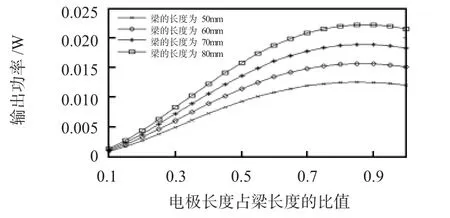
图5 功率随长度比变化Fig 5 Power change with length ratio

图6 功率随质量块变化Fig 6 Power change with quality block

3 结论

1）换能器存在一个最优负载使得输出功率达到最大值。例如:当梁的长度为80 mm时，最优负载为105Ω。因此，在设计后续采集和储能电路时，应尽量使电路工作在最优负载下，以提高转换效率。

2）压电片不一定要贴满整个梁，例如:梁长度为80 mm时，当电极长度为梁的0．8倍时输出功率最大。因此，在换能器的设计中，应该选择合适的电极长度以提高转换效率。

3）谐振频率随着质量块重量的增加而减小，输出功率随着质量块重量的增加而增大。因此，换能器设计中，在满足性能的前提下，可以增大质量块的重量。

4）压电层和金属层厚度的比值，压电梁的宽度存在一个合适的值使得输出功率得到提高。例如:梁的长度为80 mm，厚度比为0．3时，输出功率最大。

［1］ Lefecure E，Badel A，Richard C．Comparison between several vibration powered piezoelectric generators for standalone systems［J］．Sensors and Actuators，2006，126:405 －416．

［2］ Fang H B，Liu J Q，Xu Z Y．Fabrication and perfrom of MEMS based piezoelectric power generator for vibration energy harvesting［J］．Microelectroinc Journal，2006，37:1283 － 1284．

［3］ Round Y，Wright P K．A piezoelectric vibration based generator for wireless electronics［J］．Smart Materia and Structures，2004，13:1131－1142．

［4］ 王佩红，戴旭涵，赵小林．微型电磁式振动能量采集器的研究进展［J］．振动与冲击，2007，26（9）:94 －98．

［5］ 褚金奎，杜小振，朴相镐．压电发电微电源国外研究进展［J］．压电与声光，2008，30（1）:22 －25．

［6］ 张福学，王丽坤．现代压电学上册［M］．北京:科学出版社，2002．

［7］ 于红云，李艳秋，尚永红．用于无线传感器网络的光伏微能源系统设计［J］．功能材料与器件学报，2008，14（2）:476－480．

［8］ 李映平，赖百坛，黄 学．多层压电电源储能特性试验研究［J］．弹道报，2003，15（4）:65 －69．