自动振打除灰装置冲击接触模型有限元分析
2013-10-22喻九阳郑小涛彭常飞
喻九阳,靖 静,郑小涛,彭常飞,叶 萌
(武汉工程大学机电工程学院,湖北 武汉 430074)
0 引 言
由我校自主研发的“机械振打器”已在湖北双环、广西柳化、河南开祥等国内十几家煤气化企业成功应用.机械振打器安装在煤气化炉水冷壁上并通过敲击水冷壁而起到除灰的作用.在实践中,活塞杆端面部分经常在预期寿命中损坏而导致机械振打器无法运作.通过研究活塞杆与撞击杆的接触模型,以期进一步提高机械振打器的使用寿命.
结构的弹性冲击是一个经典的问题,在工程实践中有重要的应用背景.诸德超等[1]将弹性碰撞问题纳入振动分析过程,使用已成熟的振动响应分析方法及程序,避免了时序法选择补偿的繁琐过程.张继业等[2]研究了具有一般边界条件的杆在刚体纵向冲击下的振动问题.孟卓等[3]通过计算分析了荷载大小不变,施加速率不同时直杆的动态响应.邢誉峰等[4]给出了一种考虑非线性HERTZ弹性接触变形的线性化方法和计算步骤.关于机械振打器这种具有特殊边界条件的杆的接触问题,尚鲜有报道.因此,本文对具有不同接触模型的机械振打器活塞杆和撞击杆的冲击过程进行了模拟对比,找到了一种合理的接触模型,为机械振打器的优化提供了技术支持.
1 机械振打器的冲击模型
1.1 几何模型
活塞杆与撞击杆的纵向冲击模型如图1所示.活塞杆以速度v冲击撞击杆,撞击杆长l1,活塞杆长l2,杆的横截圆面半径r,杆的质量密度ρ,弹性模量E,泊松比λ.撞击杆左端弹簧和右端弹簧的弹性系数分别为k1和k2,其中(k1,k2≠0),右端弹簧预压缩量为l0.

图1 振打器冲击部分简化模型Fig.1 The simplified model of impact part
机械振打器相关几何参数如表1所示.

表1 振打器几何参数表Table 1 Geometric parameters of the Rapping Device m
1.2 有限元模型
采用ansys/ls-dyna进行有限元建模如图2所示.其中,弹簧k1为1个COMBI165单元,含2个节点,左端节点受全约束;弹簧k2为两个COMBI165单元,含4个节点,右端两个节点受全约束;撞击杆为14908个SOLID164单元,含9931个节点;活塞杆为15579个SOLID164单元,含17192个节点,其冲击速度为10m/s.
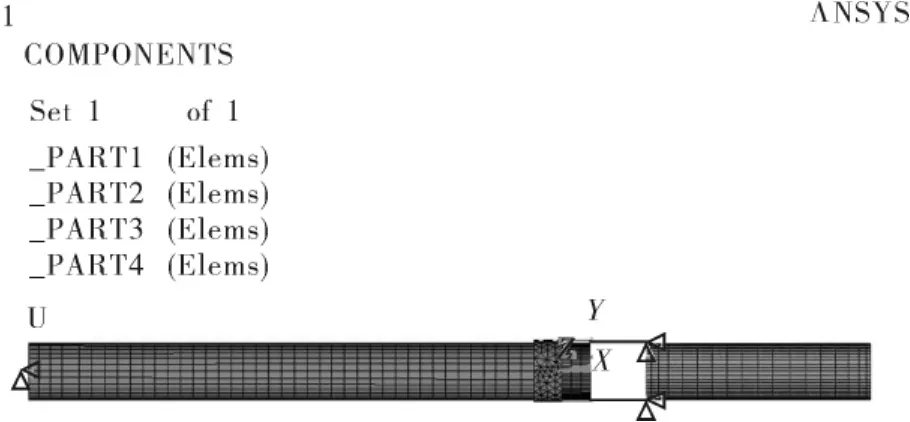
图2 振打器冲击部分有限元模型Fig.2 The finite element model of Rapping Device
机械振打器相关物理参数如表2所示.
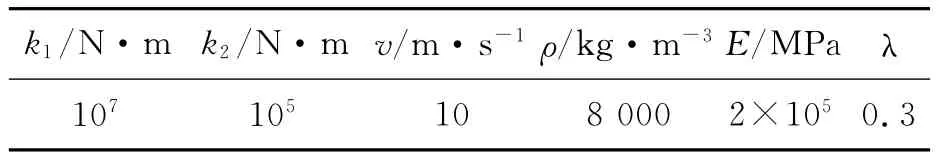
表2 振打器物理参数表Table 2 Physical parameters of the Rapping Device
1.3 计算结果及分析
在实际工程应用中,撞击杆右端面和活塞杆左端面都是使用的圆形平面.值得注意的是:由于制造工艺和安装工艺的限制,撞击杆相对于活塞杆会出现0~1°的轴向夹角α,和0~1mm的横向位移s,即0°≤α≤1°,0mm≤s≤1mm.
当s=0mm且α=1°时,活塞杆左端面上的应力分布如图3所示.
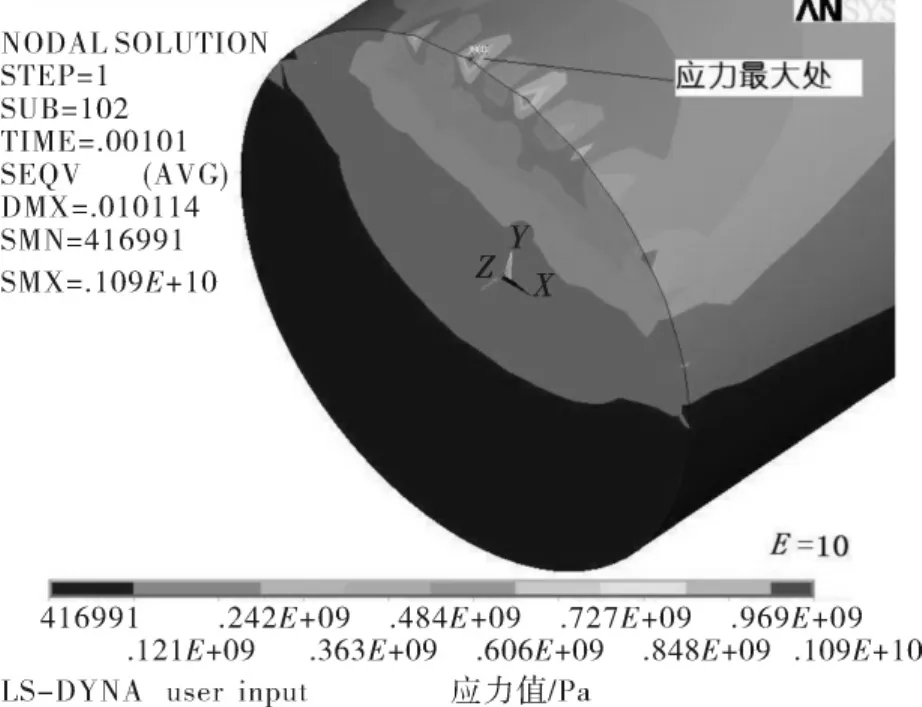
图3 s=0mm且α=1°时活塞杆左端面上的应力分布Fig.3 The stress distribution on the left end surface of piston rod when s=0mm andα=1°
由图3可以看出:端面边缘处出现严重的应力集中现象,最大应力值已达到0.109×104MPa,超过材料的许用应力.
当s=0mm时,活塞杆左端面最大应力随撞击杆轴向夹角变化的曲线如图4所示.
由图4可以看出:随着撞击杆轴向夹角的增大,活塞杆左端面最大应力显著增大,且增大到0.6°~1°时的最大应力超过材料许用应力.
当α=0°时,活塞杆左端面的最大应力随撞击杆横向位移变化的曲线如图5所示.
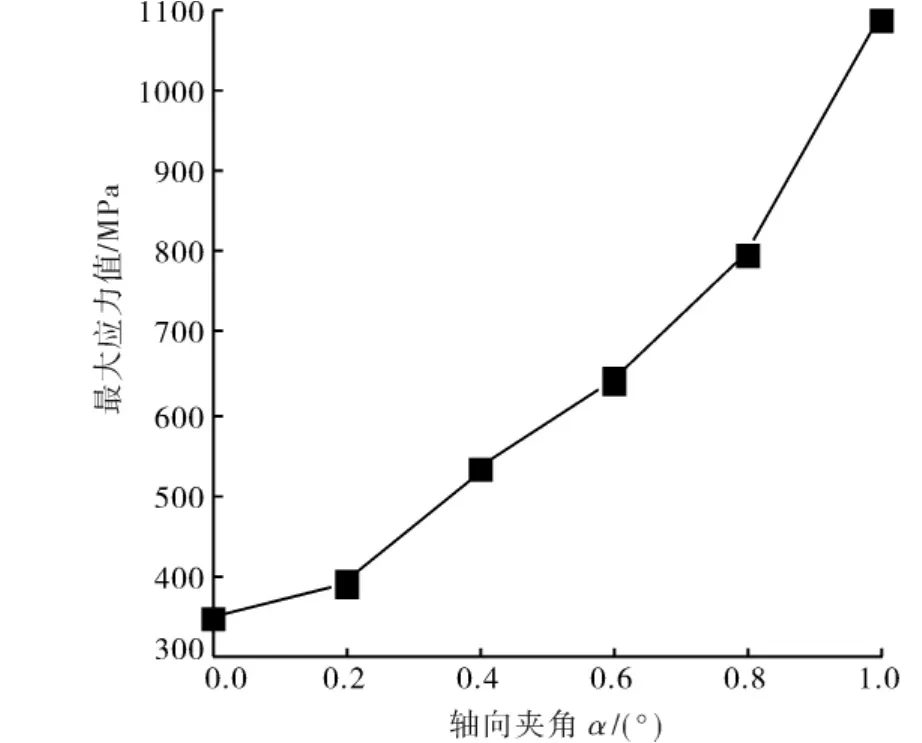
图4 s=0mm时活塞杆左端面上的最大应力曲线Fig.4 The maximum stress and axial angle curve when s=0mm


图5 α=0°时活塞杆左端面上的最大应力曲线Fig.5 The maximum stress and lateral displacement curve whenα=0°

由图5可以看出:随着撞击杆横向位移的增大,活塞杆左端面最大应力增大不明显,且一直处于材料的许用应力范围之内.
对比图3、图4和图5可以得出:导致活塞杆端面发生破坏现象的主要原因是撞击杆具有轴向夹角后引起了局部应力集中[5].
根据振打器的工作原理,为了使撞击杆具有较大的轴向冲击动能,且在撞击杆具有轴向夹角时,两杆接触时有更大接触面,可以保持撞击杆右端面为平面,而将活塞杆左端面改为球心在纵轴上的球面[6-10].
2 机械振打器冲击优化模型
2.1 几何优化模型
活塞杆与撞击杆的纵向冲击优化模型如图6所示.活塞杆以速度v冲击撞击杆,撞击杆长l1,活塞杆长l2,杆的横截圆面半径r,质量密度ρ,弹性模量E,撞击杆左端弹簧和右边弹簧的弹性系数分别为k1和k2,其中(k1,k2≠0),右边弹簧预压缩量为l0,撞击杆的轴向夹角α,撞击杆的横向位移s,活塞杆左端球面半径R,相关几何参数同表1.
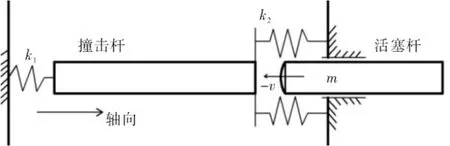
图6 振打器冲击部分优化模型Fig.6 The modified model of impact part
2.2 有限元优化模型
这里采用ansys/ls-dyna进行模拟计算如图6所示.其中,弹簧k1为1个COMBI165单元,含2个节点,左端节点受全约束;弹簧k2为两个COMBI165单元,含4个节点,右端两个节点受全约束;撞击杆为6664个SOLID164单元,含5079个节点;活塞杆为15360个SOLID164单元,含16821个节点,其冲击速度为10m/s,相关物理参数同表2.
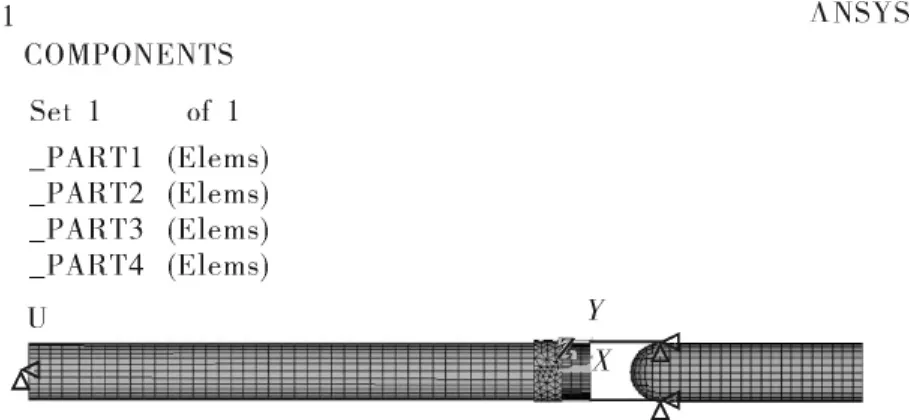
图7 振打器冲击部分有限元优化模型Fig.7 The modified finite element model of Rapping Device
2.3 计算结果及分析
当α=0°和1°时,活塞杆左端面最大应力随球面半径变化的曲线如图8所示.
由图8可以看出:1)球面半径在0.05~2m之间时,同轴碰撞下的活塞杆左端面最大应力随球面半径的增大而减小;撞击杆轴向夹角为1°的非同轴碰撞下活塞杆左端面最大应力随球面半径的增大而减小.2)球面半径在2m到无限大之间时,同轴碰撞下活塞杆左端面最大应力随球面半径的增大而减小;撞击杆轴向夹角为1°的非同轴碰撞下活塞杆左端面最大应力随球面半径的增大而增大.
对比图8和图1可以看出:球面半径增加到2m以上时,同轴碰撞下的活塞杆左端面最大应力已经无显著增大且与活塞杆左端面为平面时相差甚微.于是可以得出结论:将活塞杆左端球面的半径设定为2m最合适.

图8 α=0°,1°时活塞杆左端面最大应力曲线Fig.8 The maximum stress and spherical radius curve whenα=0°and 1°

另外,值得注意的是撞击杆相对于活塞杆可能同时具有轴向夹角和横向位移,但两者不可能同时达到最大值.为了确保以上结论的可靠性,可以假设撞击杆在具有最大轴向夹角的同时仍可以具有最大横向位移.
假定R=2m且α=1°.当撞击杆横向位移方向与撞击杆轴向夹角方向相同时,活塞杆左端面最大应力随撞击杆横向位移变化的曲线如图9所示.
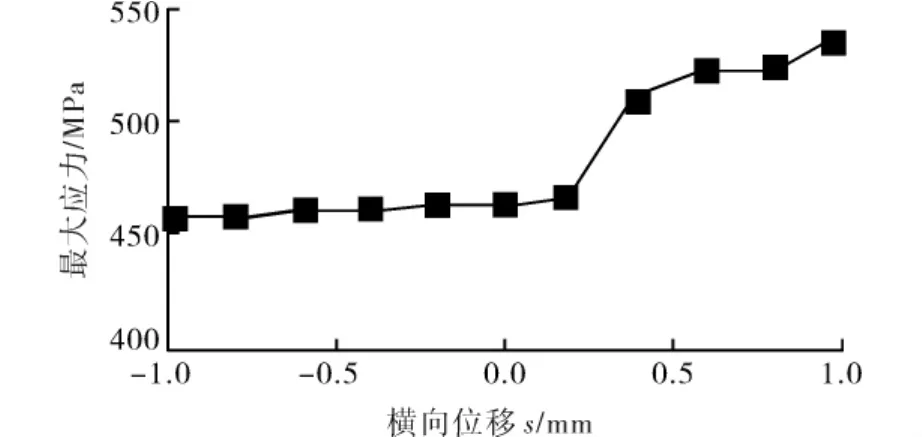
图9 撞击杆轴向夹角与横向位移同向时最大应力曲线Fig.9 The maximum stress and lateral displacement curve when the axial angle and the lateral displacement is in the same direction
由图9可以看出:撞击杆横向位移方向与撞击杆轴向夹角方向相同时,活塞杆左端面最大应力随撞击杆横向位移增大而轻微增大.
当撞击杆横向位移方向与撞击杆轴向夹角方向垂直.活塞杆左端面最大应力随撞击杆横向位移变化的曲线如图10所示.
由图10可以看出:撞击杆横向位移方向与撞击杆轴向夹角方向相同时,活塞杆左端面最大应力随撞击杆横向位移增大而变化甚微.
结合图9和图10可以得出结论:在球面半径为2m时,即使撞击杆同时具有轴向夹角和横向位移,也不会导致活塞杆左端面出现明显应力集中.
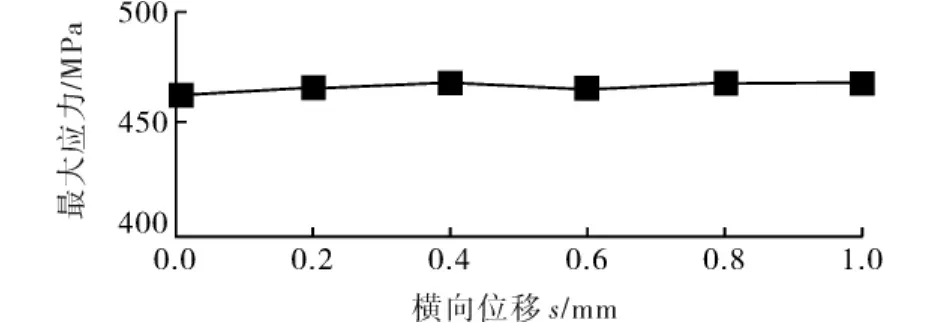
图10 撞击杆轴向夹角与横向位移垂直时最大应力曲线Fig.10 The maximum stress and lateral displacement curve when the axial angle and the lateral displacement is vertical

3 结 语
a.现有机械振打器活塞杆接触端面损坏的主要原因是:活塞杆与具有轴向夹角的撞击杆发生非同轴碰撞,导致活塞杆端面局部应力集中超过允许范围.
b.将撞击杆和活塞杆的接触模型改为:撞击杆右端面仍使用圆平面,活塞杆左端面改为球心在纵轴上且球面半径为2m的球面.改进后的接触模型可以有效避免活塞杆端面出现过大应力集中,从而将机械振打器寿命延长到设计范围.
[1]诸德超,刑誉峰.点弹性碰撞问题之解析解[J].力学学报,1996,28(1):99-103.
[2]张继业,曾京,舒仲周.杆的纵向冲击振动[J].振动与冲击,1999,18(3):57-61.
[3]孟卓,孙秦.数值模拟轴向冲击下直杆的动态响应[J].航空计算技术,2009,39(4):27-30.
[4]邢誉峰,诸德超.两杆纵向非线性弹性碰撞的瞬间响应[J].北京航空航天大学学报,1998,24(1):39-42.
[5]王成刚,王小雨.基于有限元活塞杆应力集中的研究[J].武汉工程大学学报,2011,33(11):89-95.
[6]邢誉峰,诸德超.用模态法识别结构弹性冲击载荷的可行性[J].力学学报,1995,2(5):560-566.
[7]喻九阳,高九阳.机械振打器不同往复密封结构功率损耗的分析[J].润滑与密封,2011(4):69-71.
[8]胡中功,王永建,喻九阳.煤气化装置振打除灰系统的PLC控制[J].武汉工程大学学报,2005,27(7):73-75.
[9]郑小涛,喻九阳.最佳自增强下厚壁圆筒表面轴向裂纹研究[J].核动力工程,2008(12):47-57.
[10]高九阳,喻九阳,王成刚,等.沟槽对O形圈密封结构性能的影响[J].武汉工程大学学报,2010,32(7):78-80.
