泡沫铝准静态压痕响应的数值模拟

王新筑，彭向和，郭早阳

（重庆大学煤炭灾害动力学与控制国家重点实验室，重庆 400040）

0 引言

金属泡沫材料（简称金属泡沫）具有缓冲吸能、耐高温、超轻质及结构与功能化一体等突出特点，作为一种具有潜在应用前景的新型工程材料，成为21世纪前沿材料领域的研究热点［1－5］。其中，金属泡沫的力学与吸能特性研究具有极其重要的工程实际意义。

截至目前，金属泡沫的力学性能数据多建立在受单向加载的响应基础上。单向加载试验包括常温和高温下的拉伸、压缩、弯曲试验等，对金属泡沫在局部载荷下的响应研究较少。然而在实际应用中，作为缓冲吸能材料，金属泡沫主要与各种形状的物体发生碰撞，由此会在表面产生局部凹陷变形，这种因压入而产生的凹陷变形与整体压缩变形机制存在较大区别。Andrew 等［6］通过采用不同直径的圆柱压头对金属泡沫进行了压痕试验，研究发现压痕应力随压头直径不同而变化，存在尺寸效应。Olurin［7］和王新筑等［8－9］分别研究了金属泡沫在不同圆柱直径压头和球形压头作用下的响应问题，结果表明压痕硬度和压头形状、压头尺寸及泡沫密度有关。此外，其他一些学者通过研究也发现了压痕压力是和压头形状及接触面积有关的函数［10－13］。近年来发展的连续压痕试验方法极大方便了从材料压痕试验中获得性能参 数［14－15］。Lu 等［16］进 行 了泡沫铝的动态压痕和穿孔试验及有限元模拟，模拟结果和试验数据吻合较好，并再现了压痕试验中泡沫铝的变形情况。Tao等［17］通过试验研究了颗粒大小不同的铝基复合泡沫材料在球形压头作用下的压痕响应，发现压痕应力随颗粒尺寸增大而越小。

但目前的研究都没有很好地揭示泡沫金属在压痕试验中所产生的压痕区应力场、变形情况及变形机理。为此，作者采用有限元方法对闭孔泡沫铝在圆柱形球压头作用下的压痕响应进行了数值模拟，研究了泡沫铝在圆柱形球压头作用下的位移场及应力场。

1 有限元模型的建立

对闭孔泡沫铝压痕试验进行有限元模拟时采用的是MSC／Marc有限元软件。为提高计算精度，建模时从压头与泡沫铝的接触点附近区域向远离接触点区域由密变疏进行网格划分。考虑到几何条件、边界条件及载荷的对称性，以实际模型的1／4建立了有限元模型。根据泡沫铝的自身特点，将其定义为各向同性材料。泡沫铝材料采用体单元建模，压头采用壳单元建模。泡沫铝有限元模型的力学性能参数由泡沫铝的单向平压试验确定，弹性模量E＝2.74GPa，泊松比ν＝0.33。坐标原点取在压头底部中心与泡沫铝上表面初始接触点处，试样的长、宽和厚度方向分别定义为x轴、y轴和z轴。试验中钢压头材料的弹性模量远大于泡沫铝的，因此在有限元模型中将压头定义成刚体，泡沫铝定义成变形体，且假设压头与泡沫铝之间无摩擦。由于建立的是1／4有限元模型，因此需要在相应的截面施加对称约束条件。泡沫铝的压痕试验是将试样放在刚性平压卡具上［8］，相当于刚性基础边界条件，所以在有限元模型的底部施加了约束边界条件来模拟真实的试验条件；上表面为自由边界条件。通过控制压头位移实现加载，压头移动速度为1mm·min－1。1／4有限元模型试样的尺寸为25mm×25mm×15mm，压头直径为12.7mm。在对泡沫铝进行较大压痕深度有限元计算前，需要进行单元的敏度分析，即对有限元模型按照由少到多顺序划分不同数量单元，通过对比不同单元数量的有限元模拟结果，确定最佳的有限元模型单元数量，从而确保有限元计算的精确性。最终选取的有限元模型共有10 080个单元，11 151个节点。为减小网格畸变的影响，采用了MSC／Marc有限元软件中的自适应单元［18］。图1为建立的模拟泡沫铝压痕响应的1／4有限元模型。

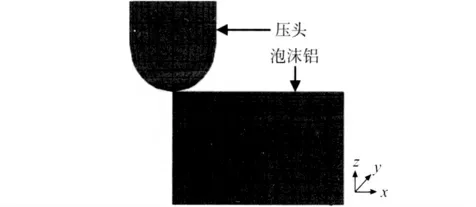
图1 模拟泡沫铝压痕响应的1／4有限元模型Fig.1 1／4FE model of indentation response of Al foam

2 模拟结果与讨论

2.1 位移分布

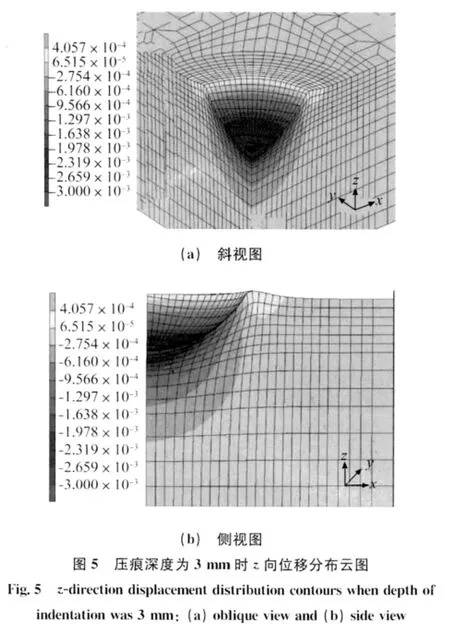
由图2，3可见，在泡沫铝与压头最底部相接触区域内的变形最大，且位移场对称分布。随着压痕深度h的增大，位移场以压痕中心向外扩展，逐渐趋近于零，变形区主要集中在压头和铝泡沫相接触的区域。在压头与铝泡沫接触的边缘，位移场有突变，这是由于与压头接触区域边缘处的泡沫铝孔壁受到压头挤压导致的。压头下方的泡沫铝变形区形状近似为椭圆形，这与文献［8］中泡沫铝压痕试验后剖开试样变形区域的轮廓形状相符（如图4所示），证明了模拟结果的准确性。分析可知，泡沫铝和压头接触区域外围的孔壁由于受到压头的挤压而发生隆起现象。为此，还提取了压痕深度为3mm时的位移云图和z向位移沿x方向的分布情况进行了证明，如图5和6所示。

图2 压痕深度为0.8mm 时的位移分布云图Fig.2 z－direction displacement contour（a）and total displacement contour（b）when depth of indentation was 0.8mm

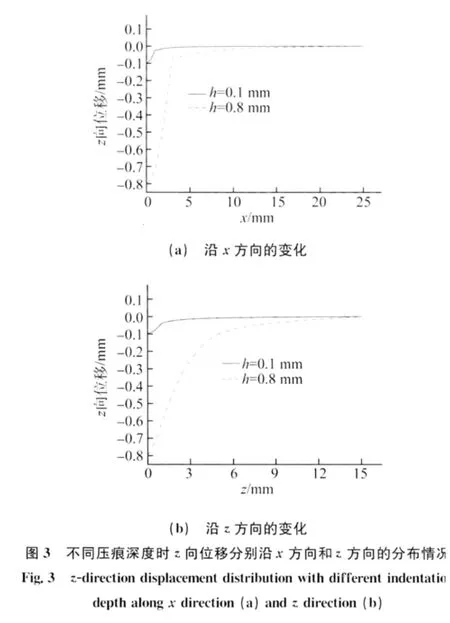
由图5和6可知，泡沫铝和球形压头接触区域外围的孔壁由于受到球形压头的挤压而发生隆起现象。泡沫铝隆起后，压头与泡沫铝的实际接触面积将大于理论计算的接触面积，但泡沫铝隆起处的位移量较小。在压痕试验时采用常规方法无法检测到这一现象。

2.2 应力与应变分布

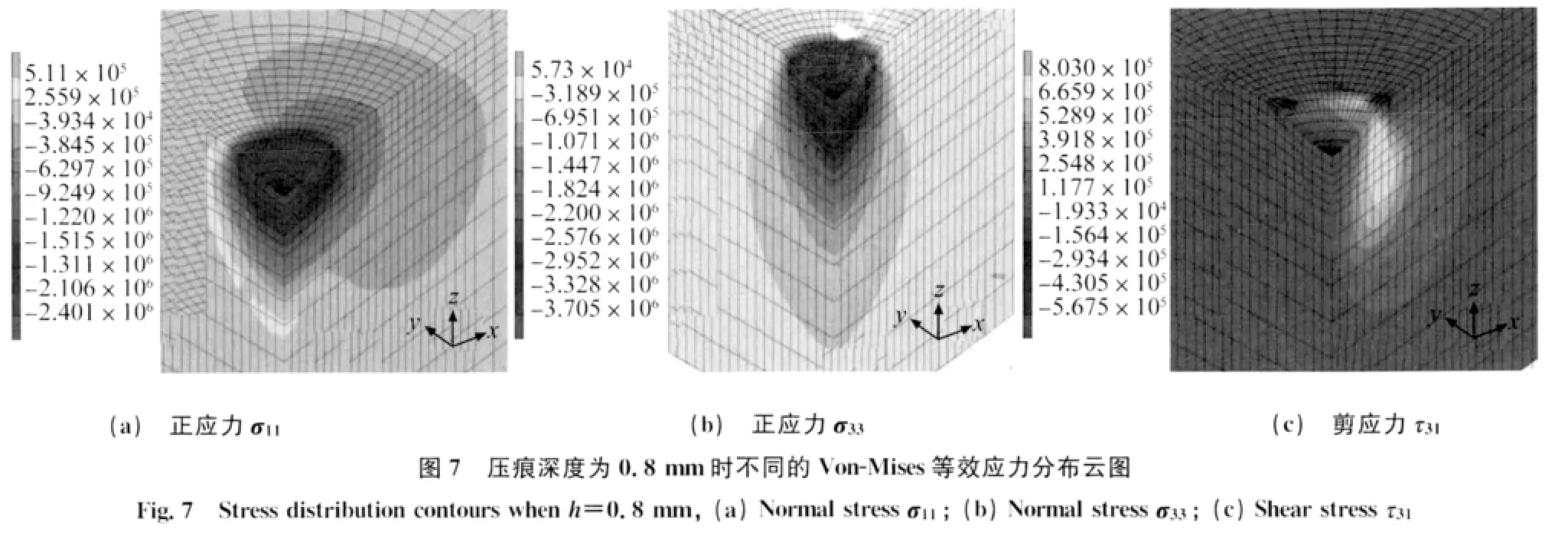
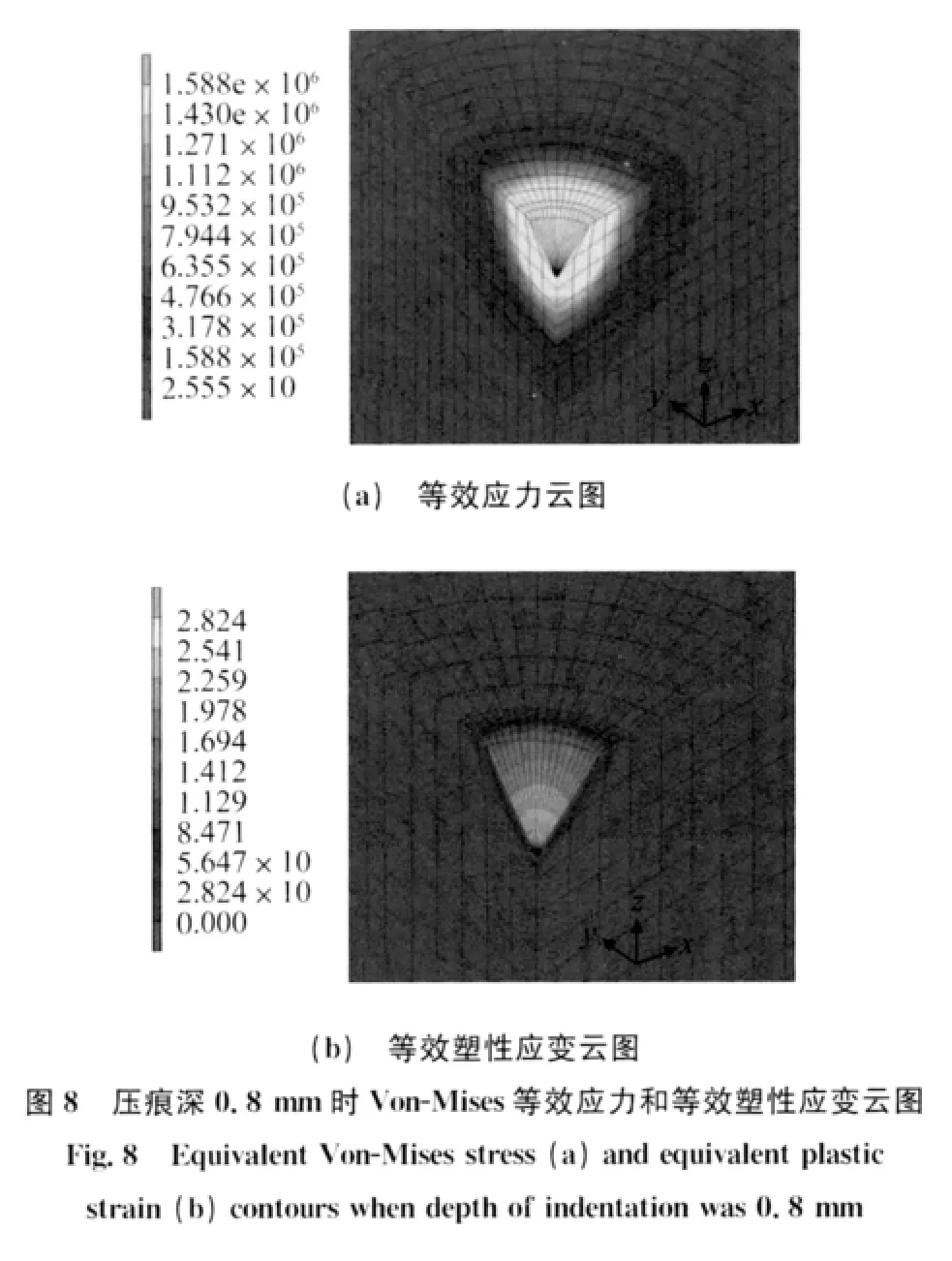
由图7～10可见，当压痕深度较小时，与压头底部中心接触的泡沫铝的应力突变情况不明显，但与压头边缘接触区域有较明显的应力突变。当压痕深度较大时，与压头底部中心及压头边缘接触区域均出现明显的应力突变。应力场主要分布于和压头直径范围相对应的泡沫铝区域内，且分布范围均随压痕深度的增大而以压痕为中心向外延伸。正应力和剪应力最大值并不是出现在压头与泡沫铝接触区域的最下方，而是位于距离压头最底部一定距离处，这是由于压头最底部接触区域的应力集中导致的。此外，压头与泡沫铝接触区域均有明显的剪应力作用，剪应力主要分布于与压头相接触区域内，这与文献［19］中泡沫铝在平压头作用下的应力情况明显不同。正应力σ33仍然是主导应力，在整个有限元模型中均为压应力，但剪应力最大值与正应力σ33最大值的比明显小于泡沫铝在平压头作用时的情况。

由图8～10还可知，当压痕深度为0.1mm 时，与压头最底部接触处的泡沫铝的Von－Mises等效应力最大，已达到泡沫铝的屈服强度，该处的泡沫孔壁发生不可恢复的塑性变形。随着压痕深度的增大，Von－Mises等效应力以压痕最底部为中心向外扩展，主要集中于压头下方区域，与压头底部相接触处区域内发生塑性屈服的孔越来越多。

2.3 试验验证

由图11可知，在相同的试验条件下，压痕深度随载荷变化曲线的有限元模拟结果与试验结果［6］吻合较好，最大误差为11.6%，这说明建立的有限元模型可用来预测泡沫铝的压痕响应。导致有限元模拟结果与试验结果之间存在偏差的主要原因有：①试验所用的压头并非像有限元模拟中假定是完全刚体；②有限元模拟时，压头与泡沫铝之间假设无摩擦力，但压痕试验时，它们之间存在摩擦力，会对压痕响应产生一定的影响；③在压头挤压下，泡沫铝会发生沉陷或隆起现象，压头与泡沫铝真实接触面积和理论计算的接触面积有一定偏差；④有限元建模时，泡沫铝模型底部施加的边界条件是平动和转动都被约束住的，相当于是固支边界条件，但实际试验中，泡沫铝在刚性基础上并不是严格地被完全限制，因为刚性基础不会提供拉应力给泡沫铝试样。

3 结论

（1）在圆柱形球压头作用下，与压头接触区域边缘的泡沫铝发生隆起，这在压痕试验中采用常规方法无法检测到。

（2）对于圆柱形球压头，泡沫铝的位移场主要集中在压头直径范围内，在压头边缘与泡沫铝接触处均出现位移突变；压头下方的泡沫铝变形区形状的模拟结果与试验结果相吻合。

（3）在圆柱形球压头作用下，泡沫铝的应力场主要分布在和压头直径范围相对应的区域内，且分布范围随压痕深度的增大而以压痕为中心向外延伸；当压痕深度较大时，圆柱形球压头最底部接触的泡沫铝变形区的应力有突变，正应力和剪应力最大值并不出现在压头与泡沫铝接触区域的最下方，而是位于距离压头最底部一定距离处；压头与泡沫铝接触区域均有明显的剪应力作用，剪应力主要分布在与压头相接触区域内。

［1］GIBSON L J.多孔固体：结构与性能［M］.刘培生，译.北京：清华大学出版社，2003：6－12.

［2］刘培生，陈祥.泡沫金属［M］.长沙：中南大学出版社，2012：5－8.

［3］BANHART J，ASHBY M F，FLECK N A.Cellular metals and metal foaming technology［C］／／Proceedings of the 2nd International Conference on Cellular Metals and Metal Foaming Technology.Bremen：Verl MIT Publ，2001：187－193.

［4］阿什比.泡沫金属设计指南［M］.刘培生，译.北京：冶金工业出版社，2006：6－24.

［5］左孝青，周芸.多孔泡沫金属［M］.北京：化学工业出版社，2005：6－12.

［6］ANDREWS E W，GIOUX G，ONCK P，etal.Size effects in ductile cellular solids—Part II：Experimental results［J］.Int J Mech Sci，2001，43：701－713.

［7］OLURIN O B，FLECK N A，ASHBY M F.Indentation resistance of an aluminium foam［J］.Scripta Mater，2000，43：983－989.

［8］王新筑，吴林志，王世勋.闭孔铝泡沫在静压痕下的力学响应［J］.复合材料学报，2010，27（2）：77－83.

［9］王新筑，吴林志，王世勋.闭孔泡沫铝在圆柱形平压头下的压痕性能［J］.机械工程材料，2009，33（6）：64－68.

［10］ONCK P R，ANDREWS E W，GIBSON L J.Size effects in ductile cellular solids—Part I：Modeling［J］.Int J Mech Sci，2001，43（6）：681－699.

［11］TULLIANI J M，MONTANARO L，BELL T J，etal.Semiclosed－cell mullite foams：preparation and macro and micromechanical characterization［J］.J Am Ceram Soc，1999，82（4）：961－968.

［12］STUPAK P R，DONOVAN J A.Deformation and energy absorption of polymer foams as a function of 2－D indenter and absorber geometries［J］.Polym Eng Sci，1994，34（10）：857－864.

［13］GIANNAKOPOULOS A E.Elastic and viscoelastic indentation of flat surfaces by pyramid indentors［J］.J Mech Phys Solids，2006，54：1305－1332.

［14］VANDAMME M，ULM F J.Viscoelastic solutions for conical indentation［J］.Int J Solids Struct，2006，43：3142－3165.

［15］LUO J，LIN J.A study on the determination of plastic properties of metals by instrumented indentation using two sharp indenters［J］.In J Solids and Structures，2007，4：5803－5817.

［16］LU G，SHEN J，HOU W，etal.Dynamic indentation and penetration of aluminium foams［J］.Int J Mech Sciences，2008，50：932－943.

［17］TAO X F，SCHLEYER G K，ZHAO Y Y.Indentation tests on Al matrix syntactic foams［C］／／Proc IUTAM Symposium on Mechanical Properties of Cellular Materials.Eindhoven：IUTAM Bookseries，2009：97－104.

［18］冯超，孙丹丹，陈火红.全新Marc实例教程与常见问题解析［M］.北京：水利水电出版社，2012：24－36.

［19］WANG X Z，ZHOU G T.The indentation behavior of closedcell Al foam under the flat－end cylindrical indenter［J］.Materials Science Forum，2012，704／705：960－966.