基于可逆逻辑电路的脉冲分配器设计

周影辉，王友仁

（南京航空航天大学 自动化学院，江苏 南京 210016）

随着集成电路规模的增加，其能耗问题已经愈发引起研究者的注意。Bennett[1]最早证明能耗来源于计算过程中的不可逆操作，传统数字电路由于不可逆计算导致信息的擦除导致能量的消耗，Landauer[2]指出，每一个信息位的丢失对应KT*Ln2 焦耳的热量产生，式中K 是波尔兹曼常量，T 是绝对温度。虽然单个信息位散失能量很少，但对于超大规模集成电路，功耗不能忽略。如果组成电路的所有门均能够执行可逆计算，即不存在信息位的擦除，理论上可以实现集成电路的零损耗。目前广泛研究的量子运算是一种具体的可逆计算，即能够从根本上解决集成电路功耗问题。

量子计算可以由可逆逻辑电路实现，现有的研究对可逆逻辑电路研究很多，但大都集中在可逆组合逻辑电路方面[3-5]，时序逻辑电路方面研究的比较少[6-8]，文献[6]首次提出了可逆触发器的设计方法，但没有考虑电路的性能指标。文献[7]提出了可逆主从触发器的设计方法。文献[8]设计了对数式移位寄存器设计方法，但是仅能适用于此类寄存器。现在没有通用的设计方法可以适用不同种类的可逆时序逻辑电路设计。

针对可逆逻辑电路现有的问题，提出了一种方法，将传统的不可逆时序逻辑电路转化为可逆时序逻辑电路。并且以典型的可逆时序逻辑电路中的脉冲分配器的设计方为例，设计了可逆脉冲分配器，通过将不可逆脉冲分配器中的基本逻辑门替换成可逆逻辑门，达到将不可逆时序电路转换为可逆时序电路的目的。

1 可逆逻辑电路的基本概念

量子计算机中，信息的基本单元是量子比特，即量子位，信息的基本操作元件是可逆逻辑门。量子比特是信息的载体，量子比特的信息经可逆逻辑门操作处理后，最后得到计算结果。

定义1 组成可逆逻辑电路的基本单元必须是可逆逻辑门，并且还需要满足以下约束条件：1）电路中无扇入扇出操作，2）输入与输出位数相等，3）对应电路真值表满足一一映射。

定义2 任何一个较复杂的可逆逻辑门均是由或基本可逆逻辑门构成。量子代价用来衡量一个量可逆逻辑电路的复杂性，用实现一个可逆逻辑电路所需要的或者 基本可逆逻辑门的数量表示，不管内部结构如何，一个基本可逆逻辑门的量子损耗是1。

定义3 在可逆逻辑电路中，除期望输出外的剩余输出称为垃圾位。垃圾位是无用输出位，也是电路能耗产生的根源。因此垃圾位数量的多少是评价可逆逻辑电路的一个最重要的性能指标。当添加垃圾位输出后，为使量子可逆逻辑电路的输入输出位数相等，需在输入端添加一定数量的常量输入，常量输入的位数也影响到可逆逻辑电路综合的量子代价，常量输入取0 或1。

常用可逆逻辑门如图1 所示。

图1 常用可逆逻辑门Fig.1 Common reversible logic gates

Feynman 门（FG 门）有两个输入量子比特，分别是控制量子比特和目标量子比特。它所实现的功能为当控制量子比特为0 时，目标量子比特不变；而当控制量子比特为1 时，目标量子比特将反转。FG 门的线路如图1（a）所示。其中，P、Q为FG 门的两个输出量子比特，FG 门能够实现线路的复制功能。当B=0 时，可得到两个相同的输出A。因此，FG 门能够实现可逆逻辑量子比特的复制。

F2G 门又叫做Feynman Double gate）F2G），有3个输入比特，能完成输入比特的两位复制。

FRG 门，又称受控交换门，是一种三输入输出的可逆逻辑门，如图所示。当控制端为0 时，FRG为三输入输出的直通门，即P=A、Q=B、R=C。当控制端A 输入信号为1 时，P=A，Q=C，R=B。

TG 门是最常用的多比特可逆逻辑门，输入位由两个控制比特位和一个被控比特来构建符合特定要求的可逆逻辑电路。此外，门可以通过修改控制位数量，构成具有不同数量控制位TG 门系列，以此来构建符合特定要求的可逆逻辑电路。

2 可逆脉冲分配器的设计

在传统的不可逆时序电路中，使用的逻辑门是不可逆的。要设计可逆逻辑电路，就要使用可逆逻辑门进行构造。本文将传统的不可逆时序电路中的逻辑门替换成可逆逻辑门，不改变原有电路的设计原理，从而将不可逆逻辑电路转化为可逆逻辑电路。

传统的可逆脉冲分配器主要是由计数器和相应的译码器组成，基于扭环计数器的脉冲分配器如图2 所示。其中计数器又由触发器级联而成，所以要将其中的触发器和基本的与门转换成相应的可逆逻辑门，另外，由于可逆逻辑电路不能有扇入或者扇出，所以图2 中的扇入扇出信号要用可逆逻辑门对信号进行复制。

首先要将传统的D 触发器转化可逆D 触发器。考虑到量子代价和量子门数的影响，设计了由图1 中的FRG 门、F2G门构成的可逆D 触发器，具体结构如图3 所示。

由图3（a）所示，当C 输入为0 时，输出Q 保持不变，当C输入为1 时，输出Q 和D 的信号相同。将图3（a）中的电路封装成图3（b）所示的模块。本文设计的可逆D 触发器（图3）的性能指标和文献[7]中设计的可逆D 触发器比较如表1 所示。

图2 基于扭环计数器的脉冲发生器Fig.2 Pulse distributor based on twisted ring counter

图3 可逆D 触发器Fig.3 Reversible D flip-flop

表1 D触发器性能指标比较Tab.1 The performance comparison of reversible D flip-flop designed by ours and others methods

由表1 可以看出本文设计的量子可逆D 触发器比文献[8]所用的量子门数减少了5个，量子代价减少了40，垃圾位减少了6个。在设计多位脉冲分配器时，量子门数、量子代价和垃圾位会有明显降低。

图2 所示的计数器是扭环计数器，根据设计原则，将计数器中的触发器替换成可逆D 触发器，从而设计出可逆扭环计数器。如图4 所示。

图4 可逆扭环计数器Fig.4 Reversible twisted ring counter

可逆扭环计数器和译码器共同组成脉冲分配器，译码器主要由与门构成，而可逆逻辑电路中没有相应的与门，必须用常用可逆逻辑门构造，Toffoli 门可以完成此功能，两输入的与门要三输入的Toffoli 门构成。另外，不可逆脉冲分配器的扇入扇出需要进行重新设计，每个扇入或者扇出的节点要用Feynman 门对信号进行复制。

结合图2 所示的可逆扭环计数器和图4 所示的可逆扭环计数器，构建的量子可逆脉冲分配器如图5 所示。

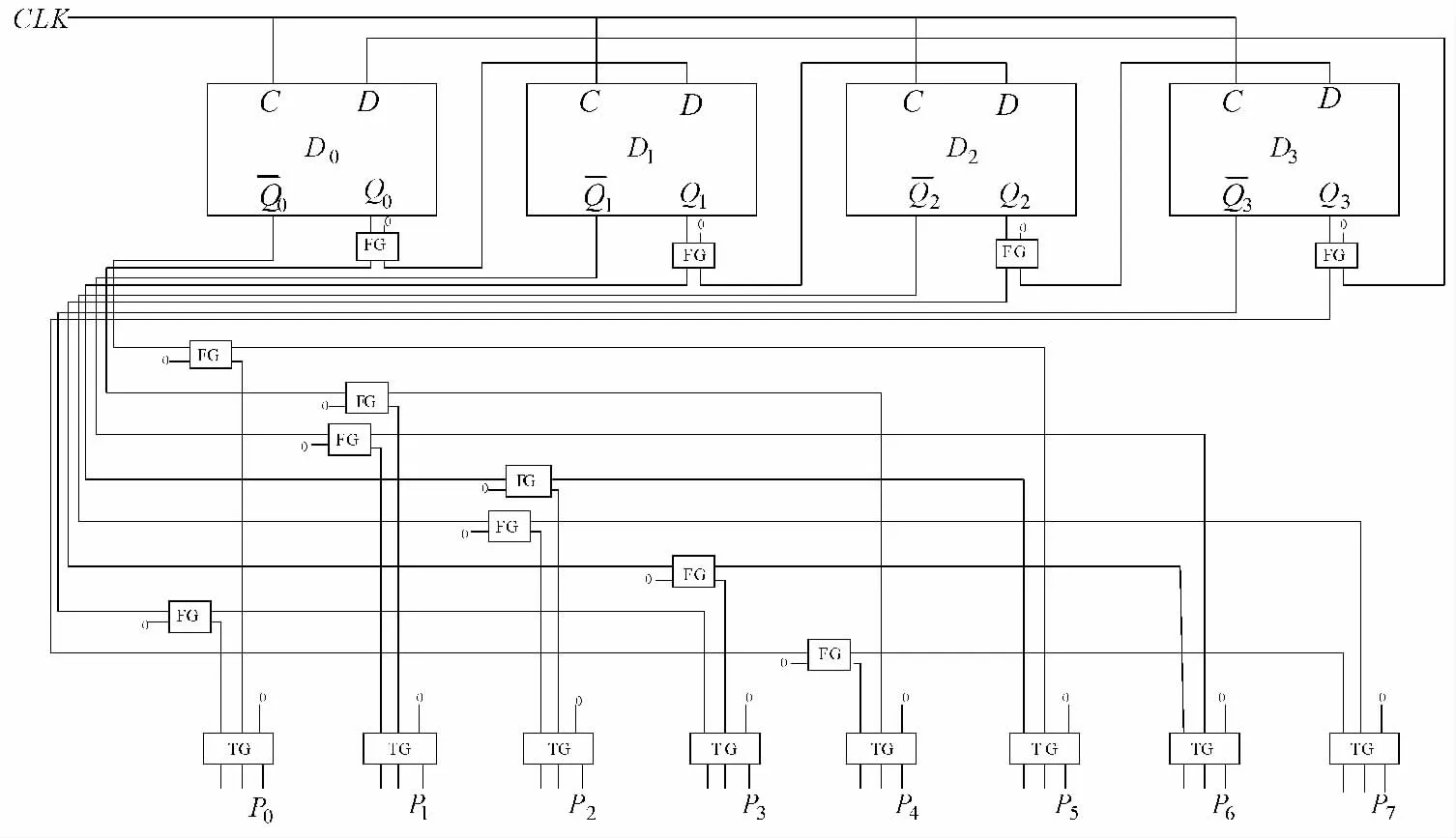
图5 可逆脉冲分配器Fig.5 Reversible pulse distributor

3 仿真结果分析和物理实现

由图5 可以看出，本文所设计的量子可逆脉冲分配器所用量子门数为32，量子代价为96，垃圾位24。

可逆脉冲分配器的结构在实验中用VHDL 进行描述封装，代码通过Xilinx ISE9.1i 下载到Spartan-6 LX FPGA 芯片上进行运行仿真，目标器件为XC6SLX9。可逆脉冲分配器的仿真结果如图6 所示。

图6 可逆脉冲分配器仿真结果Fig.6 Simulation of reversible pulse distributor

由图6 可以看出，本文设计的可逆脉冲分配器可以实现8 节拍脉冲输出功能，并且无冒险与竞争现象。

目前已经提出了多种可逆逻辑电路的物理构建方法，如利用低功耗CMOS 晶体管构建可逆逻辑门，而利用电子波导Y-分支开关）Y-Branch Switch YBS）构建可逆逻辑门可以用更少的能量改变开关状态，它的打开和关闭是通过改变电子传输两个方向中的一个，而不是切换当前的开关，在正常情况下，YBS 的一次开关动作大约散失0.6meV 的热量，一个信息位丢失所损耗的能量为KT*Ln2，大约等价为18meV，利用YBS 作为基本单元构建可逆逻辑门会更加节能[9]。如图7 所示，为利用YBS 作为基本单元构建的FG 门和Toffoli 门，由于所有的可逆逻辑电路都能有Toffoli 门实现，所以可逆脉冲分配器可以由图7 所示的可逆逻辑门设计物理电路。

4 结论

文中提出了一种可逆时序电路的设计方法，以不可逆脉冲分配器为例，将其转化为可逆脉冲分配器，分析了所设计的可逆脉冲发生器的有关性能指标并对其功能进行了仿真。另外提出了可逆脉冲分配器的物理实现方法[10]。结果表明，设计的可逆脉冲分配器能完成脉冲输出的功能。此方法还可以用于其它可逆时序逻辑电路的设计。

图7 基于YBS 的可逆逻辑门实现Fig.7 The implementation of reversible logic gate based on YBS

[1]Laudauer R.Irreversibility and heat generation of the computing process[J].IBM Journal of Research and Development，1961，5（3）：183-219.

[2]Bennett C H.Notes on Landauer’s principle，reversible computation and Maxwell’s demon[J].Studies In History and Philosophy of Science Part B：Studies In History and Philosophy of Modern Physics，2003，34（3）：501-510.

[3]管致锦，秦小麟，陶涛，等.可逆门网络的表示与级联[J].电子学报，2010，38（10）：2370-2376.GUAN Zhi-jin，QIN Xiao-lin，TAO Tao，et al.Representation and cascade for reversible gate network[J].Acta Electronica Sinica，2010，38（10）：2370-2376.

[4]吕洪君，乐亮，韩良顺，等.基于遗传算法的量子可逆逻辑电路综合方法研究[J].量子电子学报，2011，28（5）：596-604.LV Hong-jun，YUE Liang，HAN Liang-shun，et al.Quantum reversible logic circuits synthesis based on genetic algorithm[J].Chinese Journal of Quantum Electronics，2011，28（5）：596-604.

[5]Soeken M，Wille R，Hilken C，et al.Synthesis of reversible circuits with minimal lines for large functions [C].17th Asia and South Pacific Design Automation Conference，Sydney，Australia，2012：85-92.

[6]Rice J E.A new look at reversible memory elements[C]//IEEE International Symposium on Circuits and Systems，Island of Kos，Greece，2006：1243-1246

[7]Thapliyal H，Srinivas M B.A beginning in the reversible logic synthesis of sequential circuits[C]//Proc.of Military and Aerospace Programmable Logic Devices International Conference，Washington D.C.，2005，summision，1012.

[8]Rajmohan V，Ranganathan V.Design of counters using reversible logic [C]//2011 3rd International Conference on Electronics Computer Technology（ICECT），Kanyakumari，India，2011：138-142.

[9]CHUANG Min-lun，WANG Chun-yao.Synthesis of reversible sequential elements[J].ACM Journal on Emerging Technologies in Computing Systems，2008，3（4）：1-19.

[10]张伟，陈锋，马军强，等.轨/姿控发动机脉冲后效冲量快速算法的研究及应用[J].火箭推进，2012（1）：51-56.ZHANG Wei，CHEN Feng，MA Jun-qiang，et al.Research and application of fast algorithm for pulse residual impulse of divert and attitude control engine[J].Journal of Rocket Propulsion，2012（1）：51-56.