考虑不同太阳辐射模型的混凝土导流墙温度场研究

苏卫强，代 婧，李南辉，黄达海

（1.云南省水利水电勘测设计研究院，云南 昆明 650021；2.北京航空航天大学，北京 100191；3.三峡大学水利与环境学院，湖北 宜昌 443002）

0 引 言

由于混凝土的热传导性差，外界的气温变化和太阳辐射会导致混凝土内外的非线性温差，对于温度边界复杂、截面形式不规则或者约束较强等结构，会产生较大影响甚至导致开裂。目前已有大量研究关注太阳辐射对混凝土结构的温度应力效应，主要集中在桥梁、建筑领域的大跨箱梁、高耸薄壁结构和水利工程领域的拱坝、重力坝、渡槽等方面。

日照效应的研究中，边界条件的计算选取是至关重要的。边界条件主要影响因素包括太阳辐射瞬时强度、混凝土辐射吸收率、混凝土热工参数、周围环境的遮蔽等，目前都已有相关研究成果[1-4]。而太阳辐射瞬时强度的计算直接影响了温度和应力结果的准确性。由于我国很多地区缺乏太阳辐射量的观测数据，而数据的获取本身难度也很大，故很少能据实测辐射数据进行拟合，并且太阳辐射由于云量等大气因素的不定变化也具有很大的随机性。因此在研究、工程计算中主要采用晴空太阳辐射模型来计算不同地区、时间、气候类型下晴朗无云时的辐射强度。计算太阳辐射的模型很多，大多文献就直接基于某一晴空模型进行计算，而不同模型的选择是否有区别有优劣，对计算结果的影响有多大，有待进一步讨论。

本文全面归纳了计算瞬时太阳辐射强度的可采用的4种模型——ASHRAE模型、COLLARESPEREIR&RABL模型、KEHLKECK模型和HOTTEL模型 （以下分别简称 “A模型、C模型、K模型和H模型”），以及在工程中的应用方法。基于实际工程桐梓林导流墙的模型和工程参数，计算比较不同太阳辐射计算模型下的温度场，得到了连续日照对导流墙温度场的影响规律。

1 水平面太阳辐射强度计算模型

1.1 有关天文参数的计算

计算太阳辐射时，会应用到的天文参数有日角θ、赤纬角δ、太阳时角τ、太阳高度角h、太阳方位角αs，日地修正系数r，它们主要与地区纬度φ、经度J以及年序日N有关，计算公式详见文献[5]。

1.2 A模型

A模型是美国加热、空调与制冷学会推荐的晴天太阳辐射模型。该模型适用面较广，对低纬度和潮湿地区符合得较好，但对高纬度和干燥地区，其值通常要高出10%～20%[6]。该模型水平面直射强度Im和散射强度Id的计算式如下:

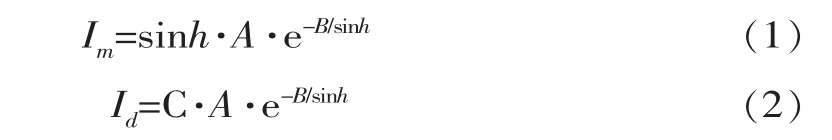
宋爱国通过对北京地区10年间太阳辐射观测数据的分析和计算，建立了北京地区晴天太阳辐射模型，A、B、C取值以年序日为自变量的多项式如下[7]:

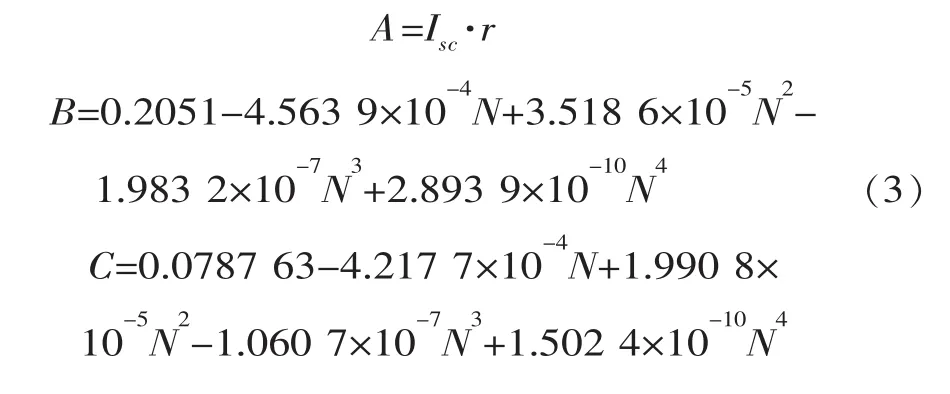
式中，Isc为太阳常数，指大气层上边界处垂直光线方向的辐射强度，取为1367 W/m2。

目前国内基于A模型的分析计算都采用此拟合值，但根据1980年～1989年的北京辐射数据建立的系数现在是否还能适用于其他地区，还未探讨。

1.3 H模型

H模型水平面的计算式如下:

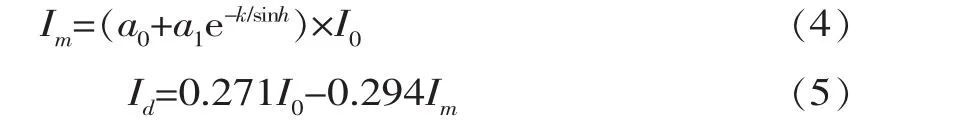
式中，I0为大气层上边界处水平面的辐射强度，由下式计算:

式（4）适用于大气能见度大于 23 km，海拔低于2500 m的情况，系数可由式（7）计算:

式中，A为海拔，km；修正因子r0、r1、rk由气候类型确定[8]。

1.4 K模型

K模型水平面的计算式如下:

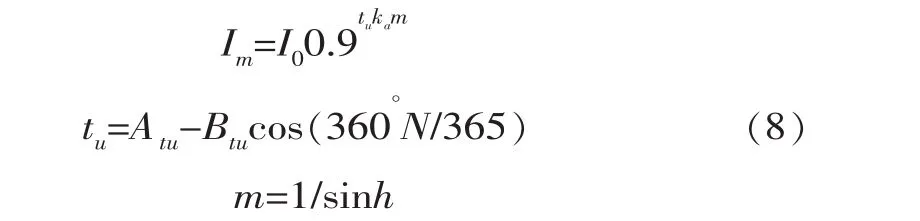
式中，Atu、Btu为经验参数，分别表示不同大气状况下，林克氏混浊度系数的年平均值和变化幅度；ka为不同海拔高度的相对气压[9]。散射强度计算采用式（5）。

1.5 C模型

在已知水平面日辐射总量的情况下，可以根据C模型求得水平面实际瞬时辐射总强度，再由式（5）就能分别求出直射和散射强度。该模型是基于日晴空指数与逐时晴空指数相等这一假设理论推导，再进行修正得到的。计算方法如下:

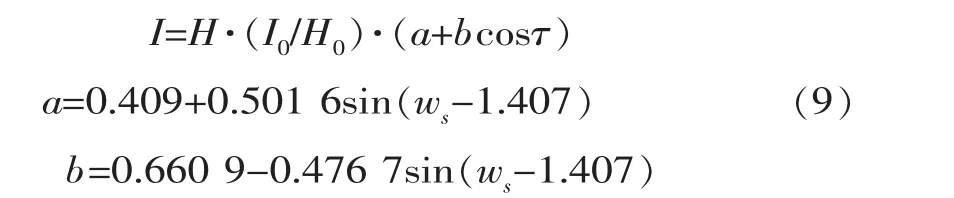
式中，H为水平面日辐射总量；I0由式（6）计算；H0为水平面天文辐射日总量，单位为W·h/m2，H0=24Iscr（wssinφsinδ+cosφcosδsinws）/π； ws为日落时角， ws=arccos（-tanφtanδ）。

目前我国气象站太阳总辐射观测较少且分布不均匀，大多观测数据只有月平均日照小时数。对于无辐射记录的地区，可根据晴空指数与日照百分比的关系计算H，因为晴空指数与日照百分比的线性相关显著，如下式:

式中，S为日照百分率，即实际日照时数与理想日照时数的比值；Kt为晴空指数，表示实际辐射量与理想辐射量的比值。a、b、Kt都是根据有观测记录气象站的实测数据回归得到的。

以晴空指数Kt、海拔高度、纬度等作为分区指标，结合我国热工分区及中国气候区划，我国可划分为5个辐射区。每区内各气象站的平均晴空指数Kt差异非常小，气候条件和区域的地理特征相似。因此对于没有太阳辐射强度记录的地方，可以在其太阳辐射分区内，选择距离最近的有数据的气象站的回归系数a、b来计算该地区的总辐射[10]。当理想大气状况下，日照百分率取为1，Kt=a+b，而晴朗天气时到达地面的太阳总辐射占理想大气辐射的90.6%[11]，因此晴空下可取H=0.9KtH0。这样就可借助国内有观测数据的气象站结果求出没有记录地区的辐射强度。

2 混凝土结构的边界条件

2.1 不同倾角与朝向的表面辐射强度

已知水平地面上的瞬时太阳直射强度Im、散射强度Id后，可以根据理论几何关系，求得不同倾角和朝向表面的辐射总强度I，工程中一般假设散射和地面反射均为各项同性。

水平面

斜面

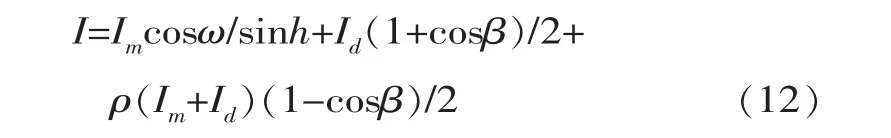
式中，β为计算面与水平夹角；ρ为地面反射率，工程计算中一般取0.20[12]；ω为斜面上光线入射角，由下式计算:

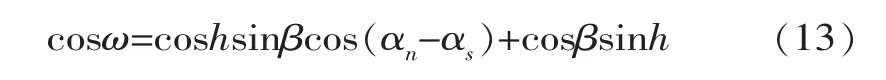
式中，αn为计算面方位角，即与南向夹角，向东为负向西为正。

2.2 混凝土结构的边界类型

2.2.1 空气边界

与空气接触边界 （包括太阳辐射）热交换的热流密度来自于太阳辐射qs、对流换热qc和长波辐射qr，采用第三类边界，方程式如下:

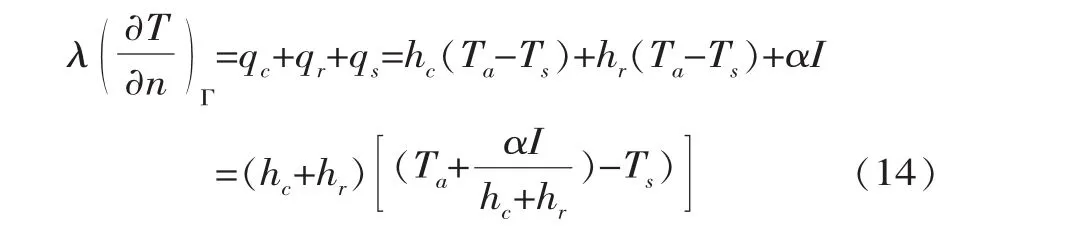
由此得到综合温度和综合换热系数，作为第3类边界计算。式中，Ta为气温，根据日平均温度及日较差采用正弦函数拟合得到；α为混凝土吸收系数，取为0.65[2]；hc为对流热交换系数，在土木工程计算中一般采用基于平均风速的经验公式求得[3]；hr为辐射热交换系数，与辐射率及瞬时表面温度有关，考虑到长波热辐射热流量不占主要部分，其值变化幅度较小，文献[13]建议近似选取固定值8.0 W/（m2·℃）。

2.2.2 水温、地温边界

水流边界及基岩的底部地温边界，一般采用第一类边界条件T=f（t）。

3 工程算例

3.1 计算参数

本文应用实际工程桐子林导流墙的模型与计算参数，分析不同太阳模型下日照对导流墙的影响。工程所在地区地理参数包括纬度101.6°，经度26.9°，海拔1000 m；混凝土热学参数包括密度2572 kg/m3，比热 1.36kJ/（kg/℃）， 导热系数 8.98 kJ/（m·h·℃），热交换系数12W/（m2·℃）；混凝土力学参数包括弹性模量28.7 GPa，线膨胀系数8.0×10-6/℃，泊松比0.17。

时间取月平均气温最高的7月10日开始，气温拟合采用式（15），水温、地温值取为当月平均温度，分别为19.3℃、29℃。

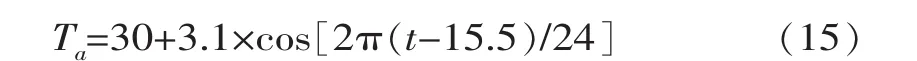
桐子林工程导流墙为南北走向，取对称截面的1/2进行分析，如图1所示，底板高14 m，宽40 m，墙高32 m，宽6 m。墙顶面水平，气温接触侧方位向东，流水接触侧向西，水位高度为底板上20 m。

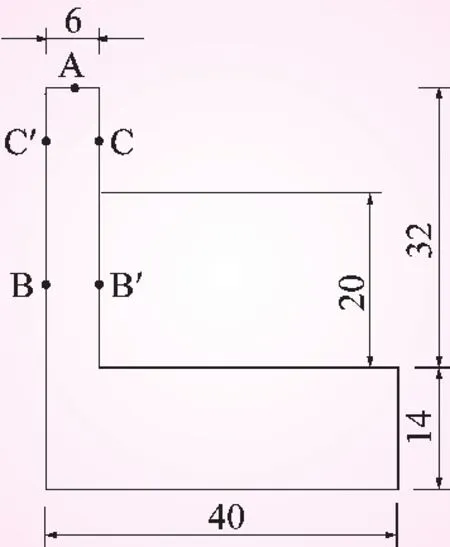
图1 模型及典型点示意（单位:m）

3.2 不同模型计算的混凝土表面辐射强度对比

由图2可以看出，顶面最大辐射强度发生在中午 1:30，A、C、K、H模型计算出的值分别为1029、1008、1152、1081 W/m2；东侧面最大辐射强度发生在上午 9:30，分别为652、642、829、779 W/m2。K模型计算的辐射强度较大，H模型次之，水平面上的辐射强度峰值，K模型比C模型大14.2%，不同模型计算的差别对于侧墙更明显，侧墙峰值最多相差187 W/m2。此外，日出时刻的辐射强度也相差较大，C模型与H模型的日出1小时内的辐射强度要明显高于A模型和K模型。

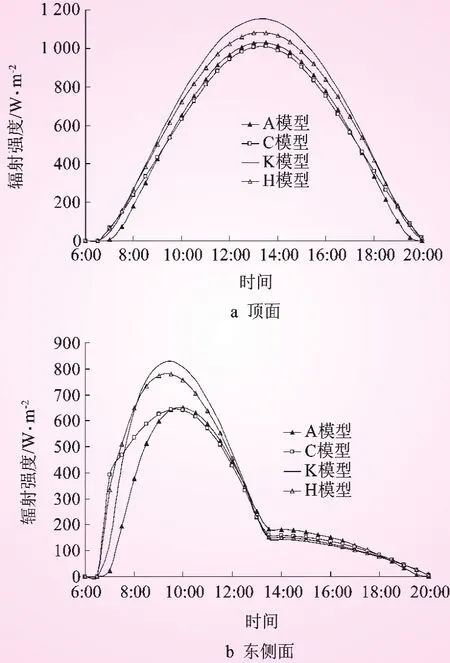
图2 不同模型计算的辐射强度

3.3 基于不同模型的连续日照后导流墙温度场

本文考虑连续6天晴朗无云的日照状况，采用ANSYS软件做瞬态温度场模拟，以稳态温度场作为初始温度，混凝土导墙的温度均取最后一天的结果。如图3所示，不考虑日照时，最高温度为30.4℃，发生在晚上8:00，最低温度为28.7℃，发生在上午7:30。连续6天日照后，A、C、K、H模型计算的水平面上A点最高气温分别为43.2、43.1、45.2、44.5℃；东侧面上B点最高温度分别为:36.3、36.8、37.8、37.7℃；西侧面上C点最高温度分别为:38.2、39.0、40.0、39.9℃。水平面受太阳照射引起的温度效应最大，西侧面次之，可见倾角和朝向对表面接受日照的效应有较大影响；对于同一点不同模型计算出的温度差别可达到2.1℃，K模型与H模型差别不大，A模型最小。

与不考虑日照相比，6天连续日照使混凝土表面最高温度最多上升了14.8℃，最低温度最多上升了7.8℃，由此可见，太阳辐射的影响不可忽略。

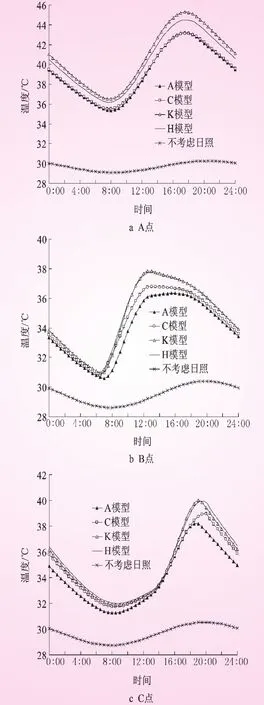
图3 不同模型计算的点A、B、C日温度变化

图4是基于C模型计算的中午12:30时的典型高程处的截面温度分布，B-B'处为一侧周期日照一侧稳定水温，C-C'两侧都有日照。6天连续日照后，可看出日照的影响深度为2 m，表面2 m以外的部位温度与初始温度基本没有变化，距表面1.5 m处温度升高了约0.5℃，距表面1 m处升高了约1℃，表面0.5 m以内受外界影响较大。因此对于薄壁结构，日照辐射易改变全截面温度，若截面形状比较复杂或有较强的约束，会带来可观的温度效应。B-B′沿厚度方向连续6天温度变化见图5，从图5可以看出，外表面1天后就能基本消除初始温度的影响。

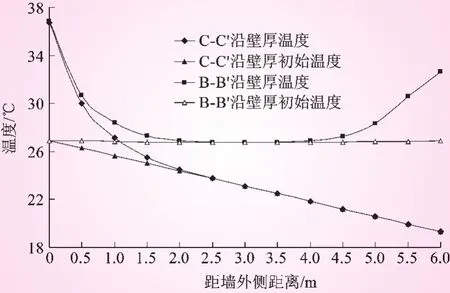
图4 B-B'、C-C'沿厚度方向的温度

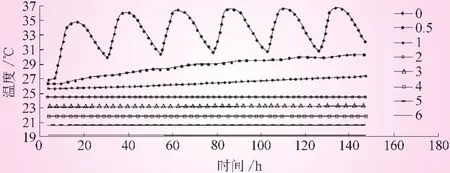
图5 B-B'沿厚度方向连续6天温度变化

4 结 论

本文分析了4个典型日照模型，并以桐梓林工程明渠导墙为例，讨论了不同日照模型下混凝土导流墙的温度场，得到以下结论:

（1）K模型形式简单但未能体现不同纬度气候的影响；A模型可适用于我国各个不同地区的参数还有待研究；H模型可考虑不同海拔和气候类型的修正，具有较普遍的适用性；C模型是基于理论推导后的修正，在能获得日辐射总量的情况下比较实用。对无辐射量统计地区，亦可借助于分区内已有辐射观测站点的参数，计算当地辐射，因此，更能吻合不同地区实际辐射量。

（2）K模型计算的辐射强度最大，H模型次之，A模型与C模型相对偏小，对于侧墙不同模型的计算值差别更明显，最多相差187 W/m2，而C模型与H模型的日出1 h内的辐射强度要明显高于A模型和K模型。6天连续日照后同一点不同模型计算出的温度差别可达2.1℃，不同模型选择，对表面外的温度差别并不明显。

（3）在平均风速为2 m/s情况下，日照使混凝土表面温度上升7.8～14.8℃，对结构的影响深度为2 m。

［1］冯小波，王长德，管光华.大型渡槽温度场边界条件计算方法［J］.南水北调与水利科技， 2008， 6（1）:170-173.

［2］刘文燕，耿耀明.混凝土表面太阳辐射吸收率试验研究 ［J］.混凝土与水泥制品，2004（4）:8-10.

［3］刘照球.混凝土结构表面对流换热研究［D］.上海:同济大学,2006.

［4］陈拯，金峰，王进廷.拱坝坝面太阳辐射强度计算［J］.水利学报， 2007， 38（12）:1460-1465.

［5］王炳忠.太阳能中天文参数的计算［M］.太阳能学报，1999（2）:8-10.

［6］李锦萍，宋爱国.北京晴天太阳辐射模型与ASHRAE模型的比较［J］.首都师范大学学报: 自然科学版， 1999， 19（1）:35-38.

［7］宋爱国，王福然.北京地区晴天太阳辐射模型初探［J］.太阳能学报， 1993， 14（3）:251-255.

［8］邱国全，夏艳君，杨鸿毅.晴天太阳辐射模型的优化计算［J］.太阳能学报， 2001， 22（4）:456-459.

［9］彭友松.混凝土桥梁结构日照温度效应理论及应用研究［D］.成都:西南交通大学，2007.

［10］王金奎.日总辐射及逐时辐射模型的适用性分析［D］.西安:西安建筑科技大学，2006.

［11］王炳忠.太阳辐射在理想大气中的衰减［J］.太阳能学报，1982，3（4）:374-379.

［12］周芳，胡明辅，周国平.铅垂面上太阳辐射计算方法探讨［J］.建筑节能， 2007， 35（195）:55-58.

［13］冯小波.大型渡槽温度荷载、冰荷载作用机理及对结构影响的研究［D］.武汉:武汉大学，2007.