异常高压气藏流固耦合的数值模拟
2013-10-20郑琴陶自强孟立新
郑琴 陶自强 孟立新
中国石油大港油田公司勘探开发研究院
异常高压气藏在开发过程中,随着气藏压力的下降,气藏岩石骨架要承受比常规气藏大得多的净上覆压力,储层应力敏感性极强,致使异常高压气藏具有比常规气藏更强的流固耦合效应。因此,研究异常高压气藏流固耦合效应的理论及方法,对于真实模拟气藏开采,指导气田生产具有十分重要的现实意义。
纵观国内外流固耦合理论的研究现状及发展动态发现,流固耦合已由简单的单相孔隙介质模型向复杂的两相或三相连续介质及拟连续或非连续介质模型发展[1-4]。在石油工业领域,流固耦合理论在解决油藏及常规气藏流体渗流及岩石小变形相互作用方面的研究较多,并且取得了较好的开发效果[5-8],而对于异常高压气藏,多数参考文献主要研究其开发动态及储层物性变化,而对流固耦合理论在异常高压气藏开发机理上的研究很少报道。目前的流固耦合模型大多采用有限差分或有限差分与有限元法联合求解[9-11],在处理复杂形状油气藏及复杂边界条件等问题上存在一定局限性,采用有限元法统一离散求解流固耦合模型的研究工作目前开展较少。
1 孔隙度、渗透率与体积应变的关系
孔隙度与岩石变形的关系:

渗透率与孔隙度、体积应变的关系为[12]:

2 异常高压气藏流固耦合模型的建立
2.1 渗流场方程的建立
2.1.1 运动方程

2.1.2 连续性方程
固体骨架的体积应变用εV=εx+εy+εz=ui,i表示,经整理可得最终整体连续性方程:
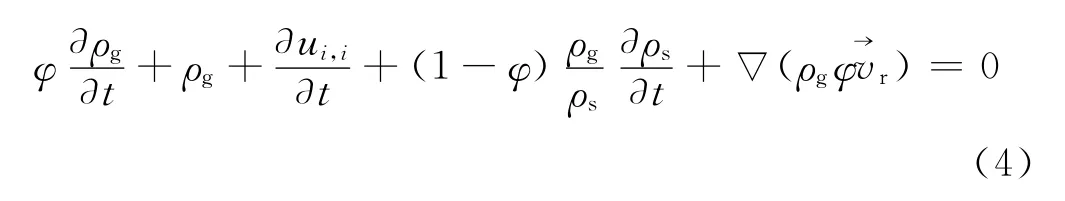
2.1.3 状态方程
气体密度的变化规律为:

2.1.4 渗流微分方程
假设是由于不可压缩的固相岩土颗粒发生相对位移后重新组合造成了固体岩石的变形,故固体密度ρs为常数,ρs对时间的偏导数为零,可对式(4)进行简化,再由式(3)可得异常高压气藏渗流微分方程:

2.2 应力场方程的建立
2.2.1 平衡方程

2.2.2 应变—位移方程(几何方程)

可写为矩阵形式ε=Lu。
2.2.3 本构方程
1)线弹性本构方程
线弹性体的本构关系是广义胡克定律,其弹性关系(即应力—应变关系)为:

也可写为矩阵形式σ′ij=Deεij。
De在三维情况下,它是含有36个元素的对称矩阵。
2)弹塑性本构方程
弹塑性应力—应变本构关系常用增量形式表示如下:
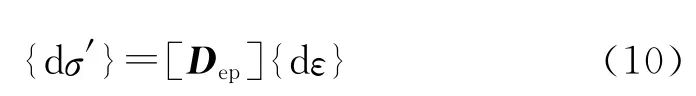
弹塑性矩阵[Dep]=[De]-[Dp],[Dp]表示塑性矩阵。
由弹塑性关联流动法则可以推导出塑性矩阵的表达式:

2.2.4 修正的应力—应变关系
Biot提出含水多孔体的应力—应变关系应该写成:

其中α被称为Biot耦合系数,δij为Kroneker符号,它定义为:δij=0,i≠j;δij=1,i=j。
2.2.5 应力场方程
由平衡方程(7),线弹性本构方程(9)以及(12)给出的应力—应变关系,先消去应力σij,再消去εij,可得用位移量ux、uy、uz表示的3个方程:

其中的变量为3个位移量和压力。
2.3 定解条件的确定
2.3.1 渗流场控制方程的定解条件
初始条件:t=0,p=pi。
封闭外边界条件:r=re,p/n=0。
定流量内边界条件:r=rw,p/n=fq(x,y,z,t)。
2.3.2 应力场控制方程的定解条件
设岩石骨架所占空间区域为Ωd(d=2或3),域边界为Ω,如果设Γu为位移边界,Γσ为应力边界,则ΩΓu∪Γσ,Γu∩Γσ=0,边界条件如下。
位移边界条件:ui|Γu=珔ui。
应力边界条件:σijnj|Γσ=珡Ti。
初始位移条件:ui|i=0=0。
3 流固耦合数学模型有限元离散
3.1 空间8节点等参元
采用空间8节点等参元对求解域进行离散。坐标变换函数式和位移函数采用统一形式
将8个不同的形函数统一表示成:

利用雅可比矩阵建立整体坐标(x,y,z)和局部坐标(ξ,η,ζ)之间的一一对应关系。即

在建立网格时,由于地层具有对称性,只需要对四分之一个区域进行研究(图1)。
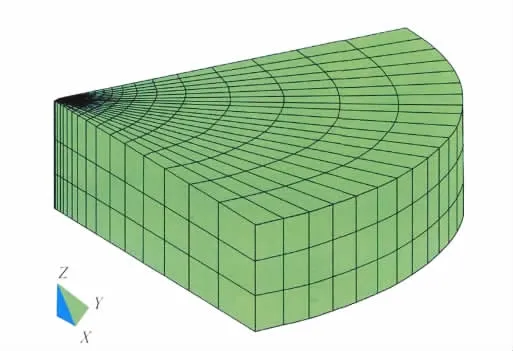
图1 空间8节点单元网格图
3.2 流固耦合应力场方程有限元离散
对8节点等参元,有u=Na、p=N珚p(珚p=[p1,p2,…,p8]),由虚功原理,经化简可得:
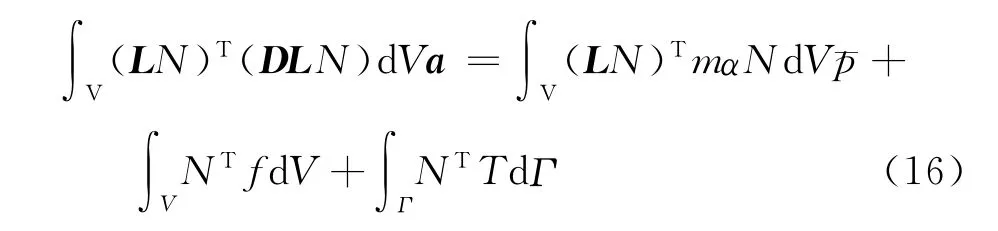
其中,三维问题的m=[1 1 1 0 0 0]T,二维问题的m=[1 1 0]T。对于弹塑性形变和塑性形变,只需将上式中的弹性本构矩阵D换为弹塑性本构矩阵[Dep]和塑性矩阵[Dp]即可。单元形式的矩阵方程为:

增量形式的单元矩阵方程有:

3.3 流固耦合渗流场方程有限元离散
3.3.1 方程的空间离散
对方程(6)进行化简可得:

取权函数为形函数N,且完全满足边界条件,通过Galerkin积分,经变换得:
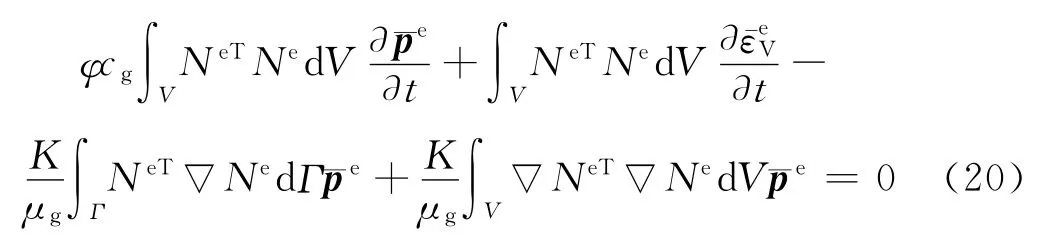
式(20)可简写为:
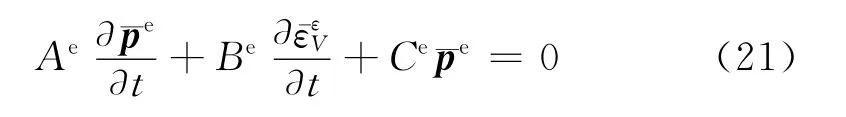
3.3.2 方程的时域离散[13]
空间离散后的流固耦合渗流微分方程含有函数、对时间的一次微分项,需进一步时间上离散。最终可得单元有限元方程:

把各单元的Ae、Be、Ce等都加以扩大到整个结构的自由度的维数,然后叠加可得到整体系数矩阵,并将单元矩阵方程组装成整体矩阵方程。
3.4 系数矩阵的确定
求解流固耦合有限元方程时,需确定有关单元系数矩阵和荷载矩阵的值,这类积分表达式中的被积函数通常包含了形函数及其偏导数的复杂组合,因此笔者采用高斯积分法来确定系数矩阵。
4 流固耦合模型算例
设原始地层压力为60MPa,初始孔隙度为10%,初始渗透率0.03D,气体原始压缩系数为1.5 MPa-1,黏度为0.35mPa·s,气藏岩石弹性模量为300MPa,泊松比为0.3,Biot系数为1.0,气层有效厚度30m,产量为1×104m3/d,井筒半径为0.1m,地层半径为1 000m。应力模型的边界条件为:①气藏外边界的垂直位移设置为零;②气藏内边界的水平位移设置为零;③气藏顶部边界设置为恒定的应力边界,其垂直应力为65MPa,水平应力为35MPa。
4.1 流体压力比较
用非耦合模型和耦合模型两种情况进行预测。求解有限元方程,得到两个模型井底处某点的压力随生产时间变化的曲线图(图2)。
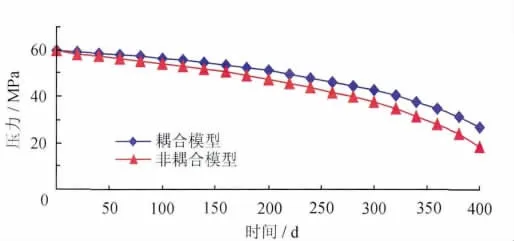
图2 压力随时间变化趋势图
图3是生产进行到300d时,井底所在平面上压力沿径向的三维分布图。由图中可看出近井地带压力的衰减比远井地带要快,形成了 “压降漏斗”。

图3 生产300 d后压力随径向距离变化趋势图
4.2 储层位移比较
图4、5表示不同时刻水平位移及垂直位移与径向距离的关系。

图4 不同时刻水平位移与径向距离的关系图

图5 不同时刻垂直位移与径向距离的关系图
5 结论
1)如图2所示,气藏采用衰竭式开采,孔隙压力逐渐减小,且非耦合模型的孔隙压力下降比耦合模型要快。因此,气藏渗流与应力的耦合效应对气藏开发动态的预测有较大的影响,是不容忽视的因素。
2)由图3可知气藏应力随空间的变化规律是:井眼附近变化量较大,变化梯度也明显较大,向油气藏边界很快减小。
3)从图4、5中可以看出,只有在离井很近的地方,才会有明显的位移,离井越远,位移的幅度也就越小。
3)笔者给出了异常高压气藏流固耦合模型建立及数值求解的方法,通过求解流固耦合模型可以得到流体压力和岩石质点位移的变化规律,实例分析结果与工程实际相符合。
符 号 说 明
φ为孔隙度,%;φ0为初始孔隙度,%;εV为岩石体积应变,εV=εx+εy+εz;K为渗透率,D;K0为初始渗透率,D;珗vg为气体渗流速度,m/h;为气体相对于固体的速度,m/h;μ为天然气黏度,mPa·s;p为压力,MPa;ρg为气体密度,kg/m3;t为时间,h;ρs为固体密度,kg/m3;uii为岩石体积应变,m;ρg0为初始气体密度,kg/m3;cg为气体压缩系数,MPa-1;pi为初始压力,MPa;σij为总应力张量分量,MPa;fi为体力分量,MPa;εij为体积应变张量分量,m;ui为岩石质点的位移分量,m;σ′为固体骨架的有效应力,MPa;λ为拉梅系数;G为剪切模量,MPa;γij为剪应变张量分量,m;dσ为有效应力增量,MPa;dε为应变增量,m;[Dep]为弹塑性矩阵;a为Biot耦合系数,无量纲;F为屈服函数;A为硬化指数;Ni为形函数;ξ、η、ζ分别为局部坐标系中的变量;ξi、ηi、ζi分别为局部坐标系中节点i的坐标分量;J-1为三阶Jacobi矩阵的逆;L为应变位移矩阵;D为弹性本构矩阵;V岩石单元体积,m3;a为单元节点位移矩阵;f为单元体积力,MPa;T为单元表面力,MPa;Γ为岩石单元边界;ae为单元节点位移矩阵;珚pe为单元节点应力矩阵;Ke为单元刚度矩阵;Qe为孔隙压力载荷矩阵;为单元等效节点荷载矩阵;Δae为单元节点位移增量;Δpe为单元等效孔压增量;为n+1时间点的单元节点应力矩阵为n+1时间点的单元应变矩阵;为n时间点的单元应变矩阵为n时间点的单元节点应力矩阵;Δt为时间步长,h。
[1]TERZAGHI K.Theoretical soil mechanics[M].New York:Tihn Willey,1943.
[2]阳仿勇.变形介质气藏流固耦合渗流理论及应用研究[D].成都:西南石油大学,2005:22-58.YANG Fangyong.Theory and application research of fluidsolid coupling seepage for deformation medium gas reservoir[D].Chengdu:Southwest Petroleum University,2005:22-58.
[3]OSORIO J G,CHEN Heryuan.Numerical simulation of the impact of flow-induced geomechanical response on the production of stress-sensitive reservoirs[C]∥paper 51929-MS presented at the SPE Annual Technical Conference and Exhibition,14-17February 1999,Houston,Texas,USA.New York:SPE,1999.
[4]TORTILE W S,FAROUQ ALI S M.A framework for multiphase nonisothermal fluid flow in a deforming heavy oil reservoir[C]∥paper 16030-MS presented at the SPE Annual Technical Conference and Exhibition,1-4February 1987,San Antonio,Texas,USA.New York:SPE,1987.
[5]LEWIS R W,SUKIRMAN Y.Finite element modeling of three-phase flow in deforming saturated oil reservoirs[J].International Journal for Numerical and Analytical Methods in Geomecharics,1993,17(8):577-598.
[6]文成杨,杜志敏,唐石丹,等.裂缝—孔隙型碳酸盐岩气藏流固耦合新模型对比[J].天然气工业,2008,28(8):89-91.WEN Chengyang,DU Zhimin,TANG Shidan,et al.A comparison of new fluid-solid coupling models for fracturepore type carbonate gas reservoirs[J].Natural Gas Industry,2008,28(8):89-91.
[7]雷霆,李治平.低渗气藏变形效应的处理方法和合理生产压差的选择[J].天然气工业,2007,27(2):93-94.LEI Ting,LI Zhiping.Treatment of deformation effect and selection of reasonable production pressures differential for low-permeability reservoirs[J].Natural Gas Industry,2007,27(2):93-94.
[8]MINKOFF S E,STONE C M.Staggered in time coupling of reservoir flow simulation and geomechanical deformation:Step l - one-way coupling[C]∥paper 51920-MS presented at the SPE Annual Technical Conference and Exhibition,14-17February 1999,Houston,Texas,USA.New York:SPE,1999.
[9]FUNG L S K,BUCHANAN L.Coupled geomechanicalthermal simulation for deforming heavy-oil reservoirs[J].Journal of Canadian Petroleum Technology,1994,33(4):22-28.
[10]冉启全,顾小芸.弹塑性变形油藏中多相渗流的数值模拟[J].计算力学学报,1999,16(1):24-31.RAN Qiquan,GU Xiaoyun.Numerical simulation of multiphase flow in an elastoplastic deforming oil reservoir[J].Chinese Journal of Computational Mechanics,1999,16(1):24-31.
[11]范学平,李秀生,张士诚,等.低渗透气藏整体压裂流固耦合数学模拟[J].石油勘探与开发,2000,27(1):76-79.FAN Xueping,LI Xiusheng,ZHANG Shicheng,et al.Mathematical simulation of coupled fluid flow and geomechanical behavior for full low permeability gas reservoir fracturing[J].Petroleum Exploration and Development,2000,27(1):76-79.
[12]冉启全,李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发,1997,24(3):61-65.RAN Qiquan,LI Shilun.Study on dynamic models of reservoir parameters in the coupled simulation of multiphase flow and reservoir deformation[J].Petroleum Exploration and Development,1997,24(3):61-65.
[13]朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,1998 ZHU Bofang.Principle and application of finite element method[M].Beijing:China Water Conservancy and Electricity Press,1998.
