一种求解机组组合问题的内点半定规划GPU并行算法

2013-10-19张宁宇

电力自动化设备 2013年7期

张宁宇，高山，赵欣

（东南大学电气工程学院，江苏南京 210096）

0 引言

半定规划 SDP（SemiDefinite Programming）是线性规划的一种推广，它是在满足约束“对称矩阵的仿射组合半正定”的条件下使线性函数极大（极小）化的问题。目前为止，已有学者对SDP在电力系统优化调度中的应用作了初步研究，文献[1]使用SDP算法来求解中期水火电力系统调度问题，得到了较好的结果。文献[2-3]针对机组组合模型中存在0／1整数变量的特点，引入一种整数约束条件，同时将目标函数和各种约束条件转换成变量的二次形式，最后采用对偶变尺度算法对得到的SDP模型进行求解。SDP算法与拉格朗日松弛法[4]和传统分支定界法[5]将机组给合（UC）模型分割成上下层循环迭代求解不同，它属于一种直接求解算法，尤其是在考虑网络安全约束情况下，可将所有约束化成相应的半定矩阵形式后使用内点法求解。

内点SDP存在以下2个问题：所需内存较大，由于每个约束条件均对应一个半定矩阵，随着机组组合模型变量和规模的增加，所需的内存空间急剧增加；内点法每次迭代中求解大规模、稀疏、半正定线性方程组需要消耗大量时间。针对第1个问题，可利用半定矩阵对称、稀疏的特点，采用稀疏存储技术减少所需内存。第2个问题归纳为解Ax=b所示的大型稀疏线性方程组，解法可分为直接法和迭代法2类。直接法主要是通过对系数矩阵进行变换，如Gauss消元、Cholesky分解、QR分解等，将原方程组化为三角或三对角等容易求解的形式，然后通过回代或追赶等方法得到方程组的解。该方法一般能得到准确解，但由于固有的前推回代的特点，使得很难实现并行化，因而所需的内存与计算量均很大。迭代法可分为古典迭代法和Krylov迭代法两大类，其中，古典迭代法有 Jacobi迭代法、Gauss-Seidel迭代法、SOR等。目前很少用古典迭代法直接求解大规模稀疏线性方程组，常结合Krylov迭代法来使用。Krylov子空间方法的主要思想是为各迭代步递归构造残差向量，即第n步的残差向量rn通过系数矩阵A的某个多项式与第1个残差向量r1相乘得到。迭代多项式的选取应使所构造的残差向量在某种内积意义下相互正交，从而保证某种极小性，达到快速收敛的目的。由于迭代法的存储开销极大减少，同时每步迭代中只包括向量与矩阵的乘法和加法或者向量内积运算，便于并行加速，因此成为稀疏线性方程组并行算法研究的热点。

作为显卡上计算核心的图形处理器GPU（Graphic Processing Unit），是一种用于密集数据计算的多核并行处理器，计算单元数量要远超过CPU。已有部分学者对GPU在电力系统中的应用进行了研究，并取得了一定的成果。文献[6]把GPU应用到潮流计算中，取得了一定的加速比。文献[7-9]利用GPU实现了电力系统暂态仿真并行计算，相比传统的串行算法取得了良好的加速比。

为提高内点SDP算法中大型稀疏线性方程组的计算效率，本文提出了一种基于GPU的Krylov子空间并行算法。该并行算法针对系数矩阵稀疏、半正定的特点，采用预条件处理的拟最小残差法（QMR法），并以矩阵分块技术为基础，在CSR（Compressed Sparse Row）存储格式下由GPU实现了稀疏矩阵的Incomplete Cholesky预处理方法和所有迭代计算。实验分析表明，它是一种求解稀疏、对称、半正定线性方程组的有效方法。对10～100机24时段6个不同的算例进行仿真，结果表明：本文算法是一种十分有效的求解机组组合问题的算法，所达到的加速效果随着算例规模的增加而更加明显。

1 机组组合问题的SDP模型

1.1 SDP原理

SDP是线性规划的推广，是一种非光滑凸优化问题。将现代内点法应用于SDP后，可保证求解诸多凸优化问题时在多项式时间内收敛于最优解[10]。

SDP模型的标准形式如下。

其中，Ai、C、Z 为 n×n 实对称矩阵，A=[A1A2…Am]T；y 为 m 维向量；b=[b1b2…bm]T；“≥”表示左侧矩阵为半正定矩阵，即该矩阵的特征根均大于等于0；“·”为迹运算符，即。

比较成熟的SDP内点法有原始对偶内点法及对偶变尺度法等，本文所采用的不可行内点法属于前一类，可把一个不在可行域内的解作为初始解进行迭代运算，简化了初始化计算。

1.2 不可行内点法

求解式（1）所示的SDP原问题等价于求解其对偶问题的对数障碍问题，其一阶KKT最优条件为：

其中，X、Z≥0，用 XZ=μI代替式（2）中第 3 式（μ 为障碍因子，随着的值为相应的最优值），并利用泰勒级数进行展开，得到以下线性系统：

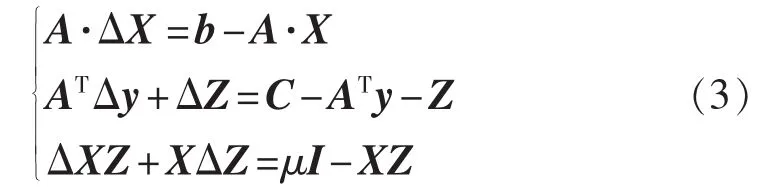
对式（3）进行求解便可得到X、y和Z的搜索方向（ΔX，Δy，ΔZ）。但是直接求解得到的 ΔX 不是对称矩阵，需引入对称化算子对式（3）中的第3式进行处理，算子如下[11]：

其中，V为需进行对称化处理的矩阵；P表示不同的搜索方向，本文取 P=Z-1／2。

得到：

其中，E=P-TZ⊗sP，F=PX⊗sP-T，⊗s为对称克劳内特积运算；svec表示将对称矩阵转化为向量的运算，smat为逆运算svec运算的逆运算，表示将向量转化为对称矩阵。消去式（5）中的ΔX和ΔZ可得：

其中，G=AE-1FAT，h=rp-AE-1（Rc-FRd）。求解线性方程组式（6）得到Δy后，便可代入式（5）求出ΔX和ΔZ，然后通过线性搜索得到迭代步长，当对偶间隙满足指定精度时中止迭代。

1.3 机组组合问题的SDP模型

本文采用文献[6]所示的机组组合模型，机组的启动费用采用传统的冷热启动三段式模型，约束条件包括机组出力约束、最小启停时间约束、机组爬坡约束、功率平衡约束和旋转备用约束等。该模型本身并非凸优化问题，原因是机组启停变量为0／1整数变量，为此引入辅助变量Q2=1，同时将0／1整数变量约束用凸二次约束u2i，t-ui，tQ=0 代替，ui，t表示机组i在时段t的启停状态，这样UC问题就可描述为一个凸优化问题，进而用内点SDP法求解。关于机组组合SDP模型的具体介绍可见文献[6]。

2 GPU

2.1 GPU结构

近年来，随着人们对计算机图像显示效果的要求越来越高，显卡上核心处理器GPU的计算量和吞吐量也越来越大。与CPU注重逻辑控制不同，GPU主要负责大规模的密集型数据并行计算。

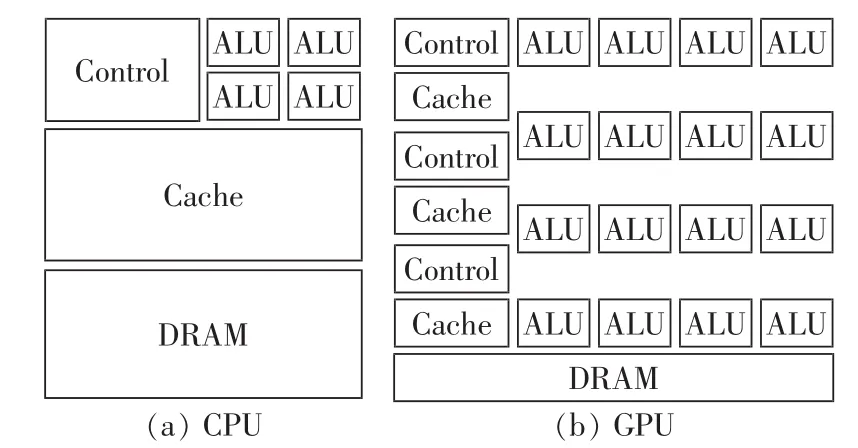
图1 CPU和GPU的结构设计Fig.1 Structure of CPU and GPU

如图1所示，CPU采用复杂的控制逻辑，用指令来控制单线程可执行程序的执行，还采用大型缓存，既可以减少访问复杂应用程序的指令和数据时产生的延时，又能够节约带宽。而GPU包含了大量的计算单元，通过多线程技术来提升运算速度与吞吐量。硬件充分利用因为等待访问内存而产生较长延时的大量线程，减少了控制逻辑中需要执行的线程，因此简化了逻辑控制和缓存单元。图中Control表示逻辑控制单元，ALU表示运算单元，Cache表示缓冲单元，DRAM表示内存单元。

2.2 统一计算设备架构编程

统一计算设备架构CUDA（Compute Unified De-vice Architecture）是NVIDIA在2007年推出的一种用于GPU的编程模型。该编程模型不需要借助于图形学应用程序编程接口（API），采用比较容易掌握的类C语言进行开发。

CUDA模型中的线程采用线程网格（grid）和线程块（block）2级结构。线程块网络和线程块中可以分别有多个线程块和线程（thread），且都有唯一的ID标志。线程是最基本的计算单元，可以分配到单个数据的计算中。以向量A[n]和B[n]相加为例，如果该程序在CPU上执行需要循环n次；当采用CUDA编程时，可以分配n个线程，单个线程根据自身ID来执行向量对应位置上元素的和运算，如A[i]+B[i]，由此实现了并行化计算。

3 基于GPU的预条件处理QMR法

原-对偶内点法求解机组组合SDP模型时，求解式（6）所示的大型线性方程组为主要步骤，矩阵G的维数等于模型的约束条件数，例如10机24时段算例的约束条件数为1488，20机算例为2928，100机算例达到14448，且呈现高维数、稀疏、对称、半正定的特点，使用直接法（如Cholesky分解）求解需要大量的存储空间以及消耗很长的时间，而Krylov子空间法作为20世纪90年代才完整提出的一类迭代法，具有存储量少、计算量少且易于并行等优点，非常适合于并行求解大型稀疏线性方程组，且结合预条件处理技术可获得良好的收敛特性和较高的数值稳定性，目前已是求解大型稀疏线性方程组的最主要方法。关于Krylov子空间法的基本原理详见文献[12]，这里不再赘述。

矩阵G具有部分特征根接近于0的特点，常用于求解对称矩阵的CG（Conjugate Gradient）法可能会导致数值的不稳定性，因此，本文采用预条件处理QMR法来求解大型稀疏线性方程组。

3.1 预条件处理的QMR法

设有n阶线性方程组：

其中，J为n×n维的实对称矩阵，k为n维向量，w为方程的解。

设w0为该方程组迭代计算的初值，算法流程如下。

a.初始化 w0，计算 r0=k-Jw0，v0=0，q0=M-1r0，ρ0=r0Tq0，n=1。

d.若 ρn-1＜ε，结束计算；否则，qn=un+βnqn-1，n=n+1，返回步骤 b。

由此可知，除去步骤c中un=M-1rn的计算，n次循环迭代的计算量主要包括n次矩阵向量乘法、3n次向量内积运算和3n次向量加减法。上述运算可通过并行稀疏矩阵向量乘法和并行向量运算在GPU上实现并行运算，故并行算法实现的难点在于使用GPU计算预处理矩阵M和实现un=M-1rn运算。

3.2 基于矩阵分块的Incomplete Cholesky预处理矩阵计算

预处理技术通过改变系数矩阵的条件数来达到加快迭代法收敛速度的目的[12]。目前为止，尚没有一种适用于所有线性方程组的预处理技术，实际计算中应根据系数矩阵的特点来设计相应的预处理矩阵。文献[14-15]根据Chebyshev多项式求出矩阵A的近似逆矩阵作为M-1，加快了收敛速度，但仅适用于强正则矩阵。文献[16]基于最小化Frobenius范数‖I-AM‖的方法来设计预处理矩阵，取得了一定的效果。文献[17]提出了一种对称超松弛（SSOR）法预处理技术，通过矩阵相乘和相加运算便可得到矩阵M。Incomplete Cholesky[18]对于正定型系数矩阵是一种有效的预处理方法，但在分解过程中前后行（列）元素之间是顺序进行的，不利于并行化计算。

基于矩阵分块技术，本文提出一种Incomplete Cholesky并行预处理方法，在CSR稀疏矩阵存储格式下使用GPU实现了预处理矩阵的并行计算，提高了计算效率。

在求解UC问题的半定规模过程中，矩阵G的结构如图2所示，考虑到对称性，只对下三角矩阵部分进行分析，阴影部分表示非0元素，对角线的元素可分为各个独立的2×2矩阵，如Fi、Bi所示。可以看出矩阵Fi之间完全独立，可进行并行Cholesky分解；分解完成后，剩余矩阵部分B中非0元素利用Fi的分解结果进行Incomplete Cholesky分解，由于B中各行元素互相独立，因此可实现并行化；计算完成后，可在矩阵B对角线上继续寻找互相独立的2×2矩阵进行并行Cholesky分解，如此循环直至得到Incom-plete Cholesky预处理矩阵M。

图2 系数矩阵GFig.2 Coefficient matrix G

矩阵G的分块流程具体如下。

a.存放分块信息的向量 Pos，flag=1，Pos[flag]=1，矩阵维数为 N，i取 2，j取 1。

b.j=Pos[flag]。

c.如果 G[i，j]为非 0 元且 i-j＞2，flag=flag+1，Pos[flag]=i，转步骤 e；否则转步骤 d。

d.如果 j＜i-1，j=j+1；否则，转步骤 e。

e.如果 i＜N，i=i+1，返回步骤 b；否则，结束计算。

实际计算中，矩阵G以CSR格式存储，分块计算中只需遍历非0元，有效减少了计算时间；此外，采用原-对偶内点法计算时，经过少数几次迭代后，矩阵G的非0元的位置便恒定下来，因此，矩阵分块信息不需每次都进行更新。以10机系统为例，Incomplete Cholesky预处理矩阵计算的循环次数从分块前的1488次降至分块后的96次，具体的计算消耗时间及加速比将在4.2中给出。

3.3 基于GPU的预处理QMR并行算法

CUDA并行计算kernel以线程网格（grid）的形式组织，每个线程网格由若干个线程块（block）组成，而每个线程块又由若干个线程（thread）组成，实质上，kernel是以block为单位执行的。

使用GPU实现基于矩阵分块的Incomplete Cholesky预处理矩阵计算如图3所示，给每个相互独立对角线上的 2×2 矩阵（F1、F2、F3、F4）分配相应线程块（block0、block1、block2、block3）进行 Cholesky分解；分解完成后，给矩阵B分配线程块（block4、block5、block6）对相应行的非0元素进行Incomplete Cholesky分解。其中，由于矩阵 F1、F2、F3、F4中计算量较小，线程块 block0、block1、block2、block3 中线程数取 32；block4、block5、block6 线程设计为二维形式，每一行线程对应于矩阵B中某一行的计算。

图3 GPU中的任务划分Fig.3 Mission decomposition in GPU

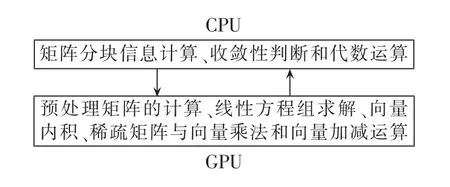
图4 CPU和GPU的主要计算内容Fig.4 Main calculation contents of CPU and GPU

图4所示为QMR并行算法在CPU和GPU中的任务划分，将可以实现并行化的计算放在GPU中，而逻辑控制功能和简单的代数运算由CPU实现，既充分利用了GPU适合密集型并行运算的优点，又发挥了CPU具有逻辑控制功能的优势。值得注意的是，GPU任务中线性方程组求解是指QMR算法中的un=M-1rn运算，求解时存在前推和回代2个过程，前推过程可以利用已得到的矩阵G的正向分块信息实现并行化，而回代过程需要对矩阵G进行一次反向的分块计算并根据得到的信息并行计算即可。

4 算例分析

4.1 开发环境及算例介绍

本文以Microsoft Visual Studio 2008和CUDA平台为开发环境，采用C语言编写了基于GPU的Incomplete Cholesky预处理QMR并行算法，并在同一平台上编写了基于CPU的Incomplete Cholesky串行分解和Cholesky直接法求解线性方程组的程序。硬件平台：CPU为Intel Core 2，主频为2.4 GHz，内存为10 GB；GPU为NVIDIA Tesla C2050，显存频率为 1147 MHz。

4.2 Incomplete Cholesky并行预处理矩阵的计算

衡量并行算法优劣的指标为所需存储量和加速比。对文中所述的Incomplete Cholesky预处理QMR而言，GPU并行算法所需的存储量明显小于CPU串行算法，因此只对算法的加速比进行分析。表1列出了对不同规模的矩阵进行Incomplete Cholesky分解时，CPU串行算法和GPU并行算法消耗的时间。可以看出，矩阵维数为1488和2928时，Incom-plete Cholesky分解的串行算法消耗的时间要小于并行算法，这是由于计算量不是太大且数据在GPU内存和CPU内存间的通信需要消耗一定的时间造成的，随着矩阵维数从2928增加到14448，系数矩阵的分块信息没有发生改变，而每次循环计算时增加的计算量可以通过增加线程块的方式实现并行化，因此 GPU并行算法消耗的时间逐渐小于CPU算法，维数为14448时可取得1.420的并行加速比。

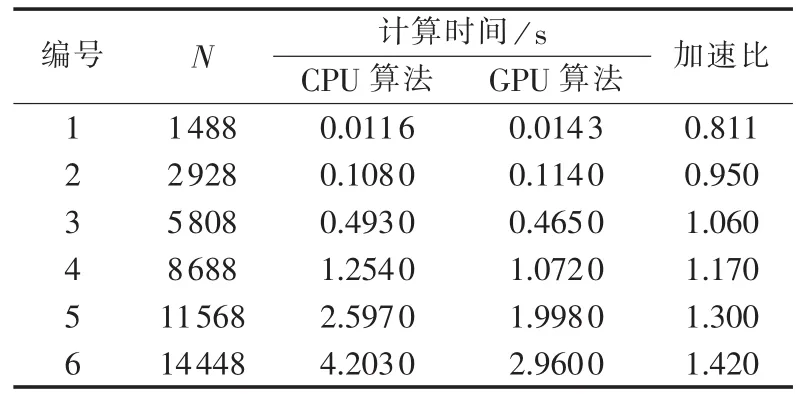
表1 不同规模矩阵的Incomplete Cholesky并行分解Tab.1 Incomplete Cholesky parallel decomposition for matrixes of different sizes

4.3 基于GPU的QMR预处理并行算法

QMR算法中的参数ε设为10-10，表2所示为Cholesky直接法和基于GPU的QMR预处理并行算法对不同规模线性方程组求解所需的时间。

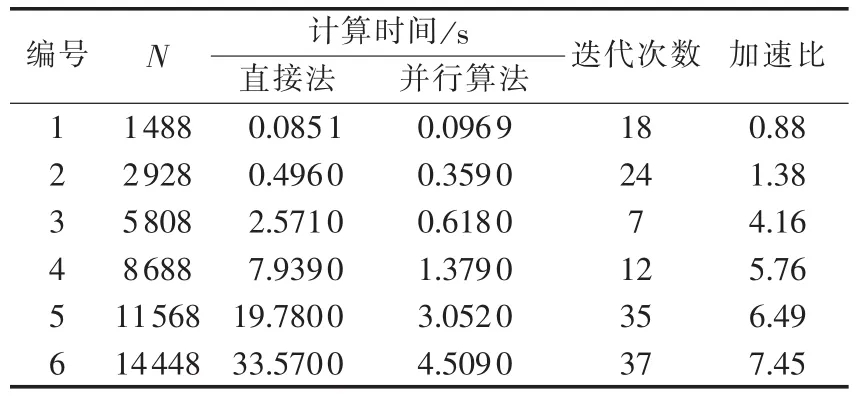
表2 不同规模的线性方程组求解Tab.2 Calculation for linear equation sets of different sizes

与Incomplete Cholesky并行算法类似，当维数为1488时，直接法的运行时间要小于并行算法，随着维数的增加，并行算法的速度优势逐渐体现出来，最终可取得7.45的并行加速比。在不同规模算例情况下，本文并行算法在经过几次迭代后可取得满足计算精度的结果，表明了算法的正确性。表3为N=8688时，QMR并行算法运行时间的分布。表中解线性方程表示使用前推和回代求解方程组；向量运算包括向量间、向量与常数以及向量内积等计算；其他部分包括CPU和GPU之间的数据传递、CPU的逻辑判断程序和CPU上代数计算等。虽然经过矩阵分块技术可以减少Incomplete Cholesky分解和使用前推回代法求解un=M-1rn的循环计算次数，然而其本身所具有的串行性质，使得其求解时间占总运行时间的绝大部分，而稀疏矩阵与向量乘法和向量相关运行运算在GPU可实现良好的并行化。

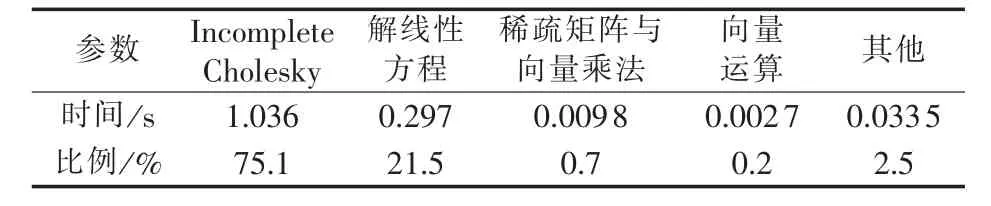
表3 QMR并行算法时间分布Tab.3 Time consumption distribution ofparallel QMR method

4.4 基于GPU的内点法求解机组组合问题的SDP模型

为了验证并行算法的有效性，采用 10、20、40、60、80和100机24时段6个测试系统，20～100机算例通过对10机算例的扩展得到，其发电机参数及各时段负荷数据见文献[19]，所有机组均考虑爬坡约束，旋转备用取系统总负荷的10%。

用SDP求解机组组合问题是一种直接求解法，不需要多重循环，也不同求解一系列子问题，可同时考虑所有的约束条件，由表4可见，通过30次左右循环计算，便可得到解结果。当算例为10机系统时，GPU并行内点算法的运行时间要略大于直接法，随着算例规模的增大，求解线性方程组式（6）的计算量逐渐增加，GPU并行算法的并行效率得到了体现，加速比从10机系统的0.95变大到100机系统的2.61。但是，由于SDP内点法除求解线性方程组外的其他计算也需要消耗一定的时间，因此取得的加速比要小于表2中的加速比。

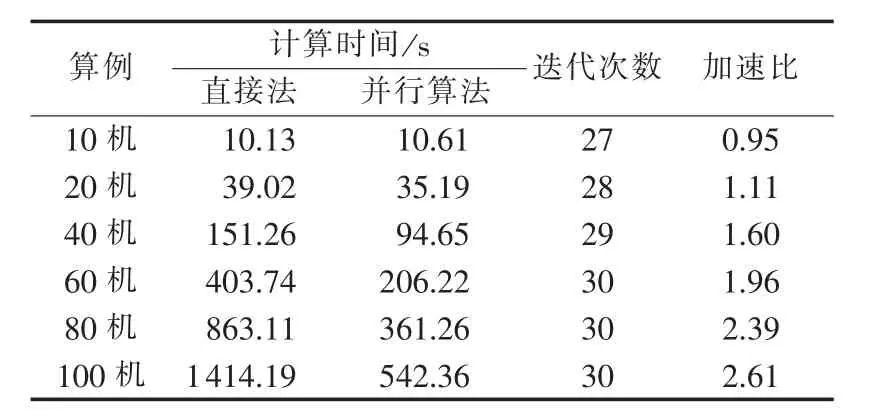
表4 不同算例的内点法计算时间Tab.4 Time consumption of interior point method for different cases

建立机组组合模型时，机组启动费用采用时间的指数函数或者冷热启动三段式费用更加符合实际情况，然而却难以转换成SDP所要求的凸优化形式，因此，在建立UC问题的SDP模型时启动费用采用固定值方式，在通过内点法求解得到机组的最优启停状态并进行经济调度时，目标函数中再加入指数或者三段式的启动费用，这样可以保证计算结果的准确性。表5所示为采用本文算法对6个算例求解得到的运行成本。表6为不考虑爬坡约束时本文算法与其他算法计算结果的对比，表中，LR、GA、EP、LRGA、GAUC分别指拉格朗日松弛法、遗传算法、进化算法、拉格朗日-遗传混合算法、基于分类的遗传算法。

可以看出，本文算法可以很好地处理爬坡约束，得到的运行费用略大于不考虑爬坡约束的情况。从表6可以看出，SDP的并行内点法每次计算只需固定的迭代次数，随机性较小，可获得稳定的计算结果，得到的费用优于部分算法，并可得到较好的近似最优解。

表5 不同系统的运行成本Tab.5 Operating cost of different systems

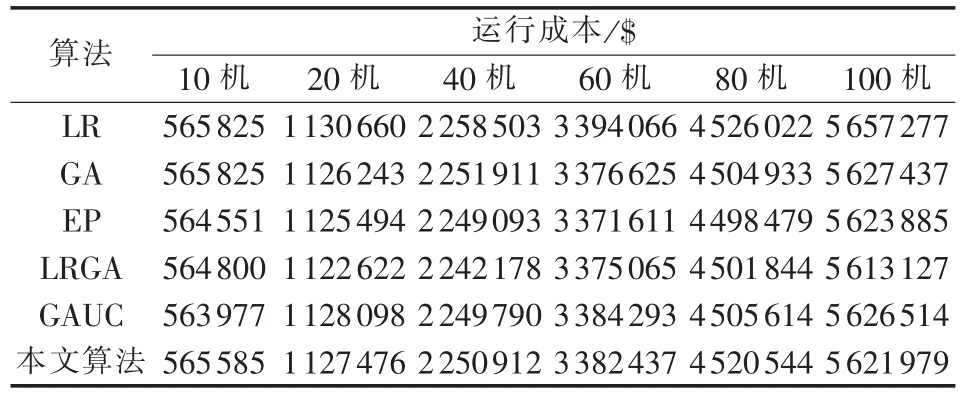
表6 各种算法计算结果的比较Tab.6 Comparison of calculating results among different algorithms

通过上面的分析，可得到以下结论。

a.基于矩阵分块技术的Incomplete Cholesky并行预处理矩阵计算，可获得一定的加速比。由于分解本身具有串行的性质，可取得的加速比有限，同时，在矩阵维数较小且计算量不大情况下，计算时间反而略大于串行算法。

b.基于GPU的QMR预处理并行算法是一种有效的大型稀疏线性方程组求解方法，可通过少数几次迭代获得解结果。Incomplete Cholesky预处理矩阵和前推回代的并行计算时间占解方程总时间的绝大部分，但该预处理法很好地处理系数矩阵半正定的特点，且在维数较大时可获得良好的加速比。

c.SDP的并行内点法可提高算法的计算效率，但如1.1节所示，除式（6）所示的大型稀疏线性方程组求解外，包括其他大量的数据处理以及矩阵和向量间的基本运算，仍需要消耗一定的时间，故算法整体的加速比小于QMR预处理并行算法求解线性方程组。在建立机组组合的SDP模型时，文中所采用的启动费用的处理方式可以很好地解决启动费用难以化成凸规划形式的问题，提高了结果的准确性。