基于非负矩阵分解的频谱感知技术研究

张梦阳，孙学斌，李 斌，周 正

(北京邮电大学信息与通信工程学院，北京 100876)

0 引言

认知无线电(Cognitive Radio，CR)［1，2］作为一种解决无线通信系统中频谱资源短缺问题的频谱感知［3］与频谱分配技术，近些年得到了广泛关注和快速发展。这一无线电技术充分利用闲置的频谱资源，采用机会接入的方式来共享频谱［4］，为解决频谱资源不足、提高频谱利用率开创了崭新的局面。

频谱感知［5］是认知无线电技术的基础和核心，在确保主用户不被干扰的情况下，可靠的检测算法为认知用户提供更多的接入空闲频谱的机会，从而提高无线通信系统的频谱利用率。目前，经典的频谱检测方法主要有:能量检测［6］、循环平稳特征检测［7］和匹配滤波检测［8］。

能量检测是一种比较简单的信号检测方法，属于信号的非相干检测，该方法根据一定频带范围内接收信号的能量判断是否存在有效的信号或仅存在噪声，接收端不需要知道任何信号的先验知识，易于实现。然而，能量检测不能区分调制信号、噪声和同频干扰，在低信噪比的情况下检测性能较差。循环平稳特征检测无需知道信号的先验信息，可以通过不同的循环频率将不同的信号区分开，在低信噪比的情况下，具有可靠的检测性能。然而，循环平稳特征检测计算复杂度高，检测周期稍长。

非负矩阵分解可将不同信号进行处理，得到相应的特征矩阵，根据特征矩阵的不同判断信号和噪声的存在情况，在低信噪比的情况下，具有较好的检测性能，同时特征矩阵与原始信号相比，维度减小，在一定程度上降低了计算复杂度。因此提出了基于非负矩阵分解的频谱感知方法。

1 非负矩阵分解

非负矩阵分解(Non-negative Matrix Factorization，NMF)［9］是1999 年由 Lee和 Seung在 Nature上发表的一篇文章中提出的，该算法是在矩阵中所有元素均为非负的条件下对其实现非负分解，传统的一些矩阵分解算法在初始输入的矩阵元素均是正数的情况下，不能保证结果的非负性，虽然从计算的观点看，分解结果中存在负值是正确的，但是在实际应用中往往没有意义，而NMF算法能够保证矩阵元素的非负性。相较于其他方法而言，NMF算法实现起来比较简单，占用的存储空间较少，产生的矩阵具有一定程度上的稀疏性，减少了数据冗余，因此NMF算法为人们处理大规模数据提供了一种新的途径。

NMF问题可描述为:已知一个非负矩阵V，要找出非负的n×r矩阵W和非负的r×m矩阵H，使V=W×H，其中r须事先给定，通常r应小于m和n，满足(m+n)r＜m·n。将矩阵看成含加性噪声的线性混合体模型:

式中，En×m为噪声矩阵，进一步可将式(1)写为:

为了求因子矩阵W和H，考虑如下的最大似然解:

如果噪声En×m为高斯噪声，此算法也可称为GKLDEM 算法［10］，似然概率为:

式中，σij=1并忽略因子 1/2和常数项∑ijlog()，则

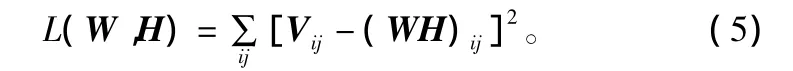
采用传统的梯度法，有

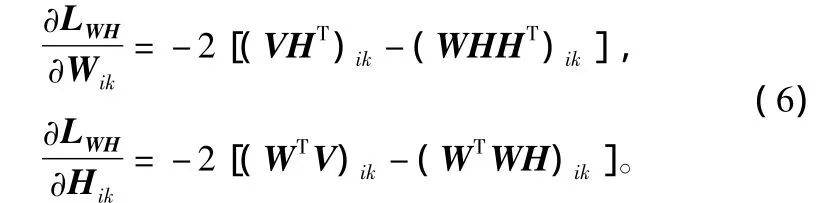
于是可以得到加性迭代规则为:

如果设置∅ik=，φkj=，则上式加性迭代规则就变成了如下乘性迭代规则:

式中的更新迭代规则已被证明是收敛的，可以通过设置一个迭代次数来控制，也可以通过计算更新前后2个矩阵的欧式距离是否小于一个给定的值来加以控制，这里采用前一种方法。

非负向量组Wn，r=［w1，w2，w3，…，wr］具有一定的线性无关性和稀疏性，从而使其对原始矩阵Vn×m的特征及其结构具有相当的表达能力，因此称矩阵Wn，r为基矩阵或特征矩阵。非负向量组Hr，m=［h1，h2，h3，…hm］称为系数矩阵，原始矩阵Vn×m可理解成基矩阵Wn，r的所有列向量［w1，w2，w3，…，wr］的权重和，而权重系数则是系数矩阵的列向量［h1，h2，h3，…，hm］，因此矩阵分解表达式如下［11］:

利用基矩阵的性质来进行频谱感知。通信系统噪声与信道传播信号在特征上存在差异，NMF将噪声与信号的特征提取出来，根据基矩阵的不同检测信道频谱占用情况。

2 基于NMF的频谱感知

主要研究了在高斯信道下的传输信号，系统模型可表示为:

式中，n=1，2，…，N，N 为观测间隔;Y(n)为感知用户接收到的实际信号;S(n)为信道传输信号;N(n)为高斯白噪声;状态H0表示该频段频谱不被占用的情况;H1表示该频段频谱被占用的情况。

检测系统首先把接收到的信号进行短时傅里叶变换(STFT)处理，得到信号的时频矩阵，然后再把时频矩阵进行非负矩阵分解(NMF)，得到基矩阵，最后通过特征检测判决频谱占用情况。NMF频谱检测框图如图1所示。

图1 基于NMF频谱检测

由图1可以看出，NMF检测方法的关键步骤是对接收信号的NMF计算。根据式(8)可以迭代计算得到接收信号的基矩阵W和系数矩阵Hy，基矩阵Wy用于特征检测，由于当检测信道不被占用时，接收信号为系统噪声，Wy呈现高斯白噪声特征的特性，当检测信道被用户占用时，Wy呈现高斯白噪声与传输信号叠加的特征的特性，因此可以根据Wy的不同特性来检测信道频谱占用情况。

假设系统信噪比SNR一定，当信道被用户占用时，理想情况下信道只存在用户信号S(n)，特征获取所得基矩阵为Ws;当信道没有被用户占用，此时只存在系统噪声，特征获取所得基矩阵为Wn。实际接收的信号是噪声与用户信号的叠加，相应基矩阵为:

式中，系数 α∞∅(SNR)，y=∅(x)为递增函数;系数β∞φ(SNR)，y=φ(x)为递减函数。

特征检测时，引入矩阵的内积A·B=＜A，B＞运算，T(Y)=Wy·Ws= ＜Wy，Ws＞ 作为检测信号特征相似性，

式中，＜Ws，Ws＞ =1，＜ Wn，Ws＞ 为常数，设为 γ，且0＜γ＜1，则式(12)变为:

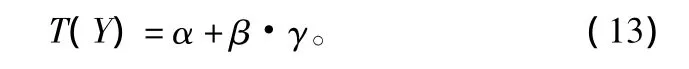
经实测，T(Y)为SNR的递增函数，T(Y)∞ψ(SNR)，y=ψ(x)为递增函数，函数仿真曲线如图2所示。

图2 信号特征相似性检测函数曲线

因此，设定门限λ，将检测信号的特征相似性与λ进行比较，判断是否存在用户信号:

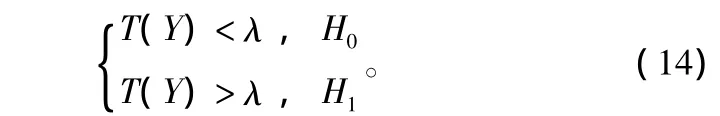
根据SNR以及用户信号的不同，门限λ也有所不同，这里根据实际情况，首先选取适量的训练样本，然后根据检测概率Pd和虚警概率Pf选取最优的门限值，以此作为后续的频谱认知过程的门限值。

3 仿真结果

下面讨论STFT-NMF检测算法的性能。待检测信号为BPSK信号，载频为20 kHz，带宽为10 kHz，采样率为160 kHz，信道所加噪声为加性高斯白噪声(AWGN)，利用蒙特卡洛仿真实验进行观测。

当采样点N=32832时，不同SNR情况下，能量检测(ET)、循环平稳检测(CT)和STFT-NMF检测(SN)算法的检测率Pd变化曲线如图3所示。

图3 3种频谱感知算法的性能对比

由图3可以看出，在低信噪比情况下(信噪比低于－15 dB)，STFT-NMF检测算法的检测性能是最好的，同时循环平稳检测和STFT-NMF检测的检测正确率明显高于能量检测。

STFT-NMF检测在信噪比SNR=－20 dB时，其检测率Pd_SN=0.95，而相同的检测率Pd_CT=0.95时，循环平稳检测所需信噪比 SNR=－18.2 dB，Pd_ET=0.95时，能量检测所需信噪比 SNR=－15.5 dB。可见STFT-NMF检测算法的检测性能比循环平稳检测和能量检测分别提高了1.8 dB和4.5 dB。

当信噪比SNR=－25 dB时，STFT-NMF检测的正确率Pd_SN=0.69，循环平稳检测正确率Pd_CT=0.57，能量检测的正确率 Pd_ET=0.53，可见在极低信噪比条件下，STFT-NMF检测具有相对较好的检测性能。

4 结束语

分析了非负矩阵的特性，发现高斯噪声与调制信号经过非负矩阵分解之后的特征矩阵存在着差异，提出了基于STFT-NMF算法的频谱认知技术，并针对所提算法进行了仿真。仿真结果表明，将STFT-NMF算法应用于认知无线电频谱感知中，在低信噪比情况下具有较其他算法更优的检测性能。■

［1］MITOLA J，MAGUIRE G Q.Cognitive Radio:Making Software Radios More Personal［J］.IEEE Personal Communications，1999，6(4):13 －18.

［2］AKYILDIZ I F，LEE W Y，VURAN M C，et al.Next Generation/Dynamic Spectrum Access/Cognitive Radio Wireless net works:A Survey［J］.Computer Networks Journal，2006，50(13):2127 －2159.

［3］LI B，ZhOU Z，ZOU W X，et al.Interference Mitigation between Ultra-Wideb and Sensor Network and Other Legal Systems［C］∥EURASIP Journal on Wireless Communications and Networking，2010:1 －15.

［4］SRIDHARA K，CHANDRA A，TRIPATHI P S M.Spectrum Challenges and Solutions by Cognitive Radio:an Overview［J］.Wireless Personal Communications，2008，45(3):281－291.

［5］WEISS T A，JONDRAL F K.Spectrum Pooling:An Innovative Strategy for the Enhancement of Spectrum Efficiency［J］.IEEE Commun.Mag.，2004，42(5):8 －14.

［6］CHEN X F，NAGARAJ S.Entropy Based Spectrum Sensing in Cognitive Radio［C］∥7th Annual Wireless Telecommunications Symposium，Ponoms，CA，United States，2008:57－61.

［7］CABRIC D，MISHRA SM，BRODERSEN RW.Implementation Issues in Spectrum Sensing for Cognitive Radios［C］∥Proc.Asilomar Conf.on Signals，Systems，and Computers，PacificGrove，CA，United States，2004:772 －776.

［8］JARMO L，VISA K，AUN H，et al.Spectrum Sensing in Cognitive Radios Based on Multiple Cyclic Frequencies［C］∥Proceeding of the 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications，CrownCom，Orlando，FL，United States，2007:37 －43.

［9］LEE D D，SEUNG H S.Learning the Parts of Objects by Non-negative Matrix Factorization ［J］.Nature，1999，401(6755):788－791.

［10］LEE D D，SEUNG H S.Algorithms for Nonnegative Matrix Factorization［C］∥Proceedings of Neural In formation Processing Systems，2001:556 －562.

［11］TANG J，GENG X Y，PENG B.New Methods of Data Clustering and Classification Based on［C］∥Business Computing and Global Informatization(BCGIN)，Shanghai，2011:432－435.