区间数判断矩阵在供电服务品质评价中的应用

冯延东，余汉华，梅玉峰

● （中机国能电力工程有限公司，上海 200061）

区间数判断矩阵在供电服务品质评价中的应用

冯延东，余汉华，梅玉峰

● （中机国能电力工程有限公司，上海 200061）

为了得到具有全局最优的区间权重，避免客户端数据缺失和常规层次分析（AHP）算法中一致性检验的数据流失，通过分析得出了供电服务质量评价体系和对专家咨询的数据，引入区间数判断矩阵取代传统单一实数矩阵来定量描述某一准则下的权重。通过对区间数判断矩阵的拟优化处理，改进了AHP过程，并引入极值点方法求解出拟优化一致矩阵的区间权重。将改进的 AHP算法运用于供电服务品质评价体系，对供电服务品质评价的优先区间权重进行了计算。与传统 AHP算法的结果对比，改进算法的结果中包含了样本全部信息，具有全局最优性，能更准确地表达多样本决策，避免了复杂的一致性检验环节。

供电服务品质评价；区间数判断矩阵；极值点法

1 供电服务品质评价体系

本文构建的供电服务品质评价体系结构如表 1所示。可以看出，选用的评价体系主要包括：形象评价、服务评价、电费抄收、供电质量、用电报装及投诉评价6个层面及19个二级指标。该评价体系结构是根据文献[3-5]中的电力客户服务内容、调研专家观点以及指标体系分析理论来构建的。

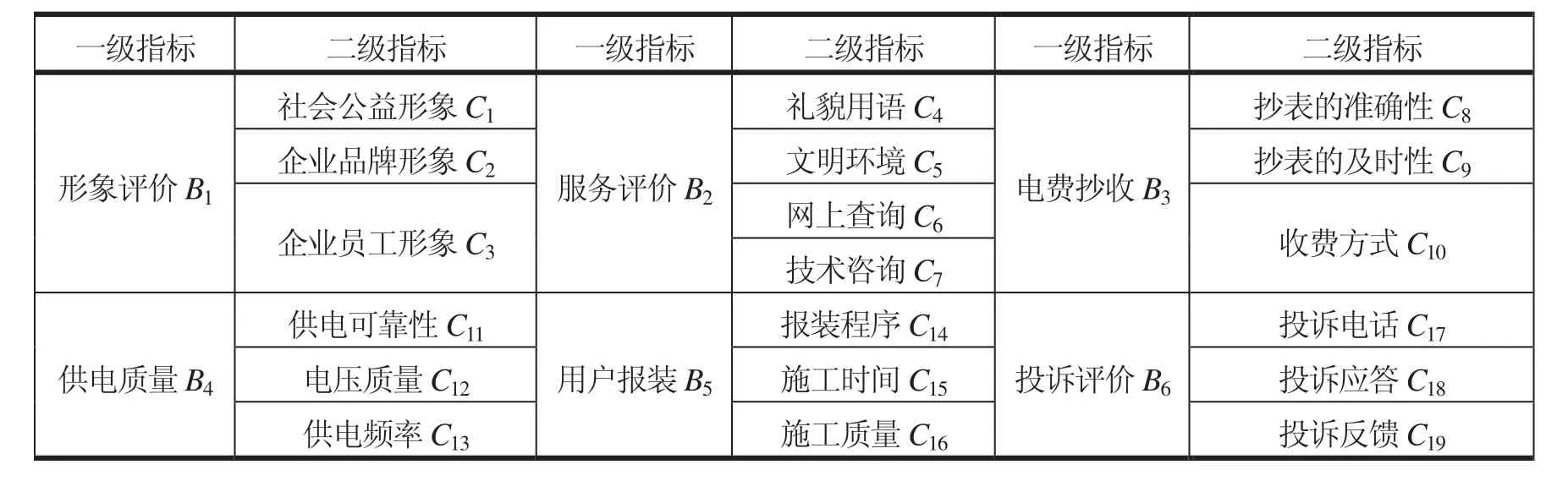
表1 客户供电服务品质评价指标体系A

2 区间权重

设权重系数分别为 θ1, θ2,…,θm且

式中：m为参加判断决策的专家人数；ijk为k(k=1,…,m )专家用单一实数对指标j对准则i的隶属权重评价。

由式（1）处理规则对数字判断矩阵重构，得到的群体区间数判断矩阵为：

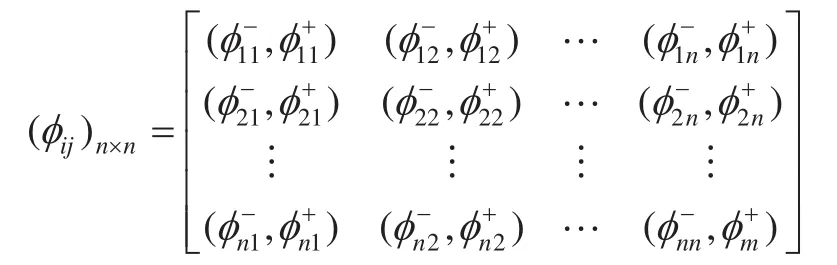
式中：对任意i, j,=1, 2, 3,…n（n为某一准则下隶属指标的个数），为区间数；和文献[6]的单一数字矩阵构成原则相同，区间数判断矩阵仍满足且对区间数规定：

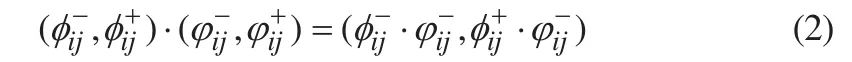
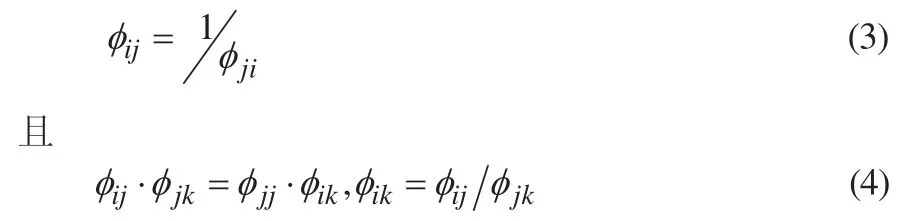
依据传统九标度 AHP算法[7-8]，结合式（1）对单一实数矩阵进行重组得出的区间数判断矩阵，经过的变换处理，既是区间一致互反矩阵，又是区间反对称传递矩阵。若存在传递矩阵使得取最小值，满足

对传统 AHP算法和正规求权重方法公式变换[9]可得：

式中：i, j,=1, 2, 3,…n（n为某一准则下隶属指标的个数)，根据求极值定理，当或者对任意求偏导数当，对任意且求偏导数判断它们的单调性来确定κ值，代入式（8）可求得区间权重的极大值、极小值。

3 评价系统

按照式（1）对电力专家咨询数据的相互关联影响以及隶属模糊关系的不同层次聚集组合，构造出区间数判断矩阵，再对区间数判断矩阵拟优化处理，结合极值点法利用拟优区间判断矩阵可以求区间权重，求解步骤如下：

步骤1：对供电服务品质评价层次结构体系分析得出区间数判断矩阵的拟优化一致矩阵。

步骤2：根据ωi的单调性判断κ的取值：

1）ωimax处κ值：在或者ωi为单调增时，κ取1；ωi为单调减时，κ取0。

2） ωimin处κ值：在或者ωi单调增时，κ取 0；ωi单调减时，κ取1；在对任意κ取0、1的组合最小值。

步骤3：重复步骤2求得其他ωi区间权重值。

步骤4：计算组合区间权重。

4 算例分析

为了验证本文所述评价方法的正确性，本节将采用matlab7.1软件对客户的服务评价和综合指标体系进行区间权重分析。根据式（1），得出客户的服务评价和综合指标体系的区间数判断矩阵分别为：

由区间数判断矩阵拟优化处理方法，运用 matlab7.1软件编程运算得客户的服务评价和综合指标体系的最优一致性矩阵为：

在各指标区间权重基础上，结合式（2）求得组合区间权重：

ω是以区间数的形式存在，说明符合要求的权重不是用单一实数，这很符合供电服务评价这样的定性分析事件的模糊性[10]。在文献[11]中，用传统AHP算法求得的单一实数权重值如下：

5 结束语

通过对区间数判断矩阵的拟优化处理得出区间数权重值，能对供电服务品质层次结构体系做出全面正确的评价。采用的拟优化一致性矩阵，克服了传统AHP算法对判断矩阵的一致性检验过程；通过用极值点法来求算区间数判断矩阵权重的方法，数据结果更准确。本文方法优于传统算法，另外区间数判断矩阵相比数字判断矩阵更能定性分析模糊决策事件，并且对该类事件的解决提供了新的思路。

[1]姜东飞. 基于客户满意度综合指标评价的电力市场营销对策[D]. 保定: 华北电力大学, 2008.

[2]伍伟华. 广州萝岗供电大客户满意度的调查与评价分析[J]. 华北电力大学学报, 2008(2): 24-27.

[3]国家电网. 国家电网公司供电服务品质评价办法（试行）宣贯培训资料[M]. 北京: 国家电网营销, 2007:3-18.

[4]陈少江. 湖南省电力公司供电优质服务文件汇编（2003-2006）[M]. 长沙：湖南省电力公司供电局,2006.

[5]湖南省电力公司. 2010年供电服务客户满意度调查结果应用[M]. 长沙: 湖南省电力公司供电局, 2010.

[6]Saaty T L, Vargas L G. University and rank order in the analytic hierarchy process[J]. European Journal of Operational Research, 1987 (32): 107-117.

[7]魏毅强, 刘进生, 王绪柱. 不确定型AHP中判断矩阵的一致性概念及权重[J]. 系统工程理论与实践,1994(4): 16-22.

[8]杜红珊, 李红杰, 郑庆玉. 不确定型AHP的最优传递矩阵法[J]. 曲阜师范大学学报, 1997, 23(4):37-40.

[9]扶元广, 张继国. 区间判断矩阵排序权重的极值点研究[J]. 运筹与管理, 2008, 17(4): 84-87.

[10]杜义贤, 田启华. 基于神经网络的模糊综合评价方法[J]. 系统工程与电子技术, 2005, 27(9): 1583-1586.

[11]吴小欢, 覃菊莹, 吕跃进. 区间数判断矩阵的一致性及权重计算[J]. 模糊系统与数学, 2007, 21(5):113-118.

Application of Interval Comparison Matrix in Electricity Supply Service Quality Evaluation

FENG Yan-dong, YU Han-hua, MEI Yu-feng

(China Sinogy Electric Engineering Co., Ltd., Shanghai 200061, China)

In order to get the interval weight with global optimization and to avoid the deficiency of client data and the loss of the data, which comes from the consistency check of the conventional analytical hierarchy process (AHP) algorithm, evaluation system of the power supply service quality and consultation data to the expert are gotten through analysis. Leading into the interval number judgment matrix replaces the traditional single real matrix to describe the weight under criteria. Through the optimization processing of interval numbers judging matrix, the process of AHP is improved. And leading into an extreme point method, the interval weight of the imitated optimal consistent matrix is solved. The improved AHP method is applied to power supply service quality evaluation system, and the interval weight of the power supply service quality assessment is calculated. Compared to the results of conventional AHP method, the results of the improved algorithm contain all information of the sample. It possesses global optimality and can express more accurately decision-making of multi-samples to avoid the check link of complicated consistency.

power supply service quality assessment; interval number comparison matrix; method of extreme point

TM726

A

0 引言

随着社会对供电服务品质要求越来越高，电网企业需要了解真实的供电服务品质。通过找出对电力营销敏感性高的指标并确定其在客户服务中的权重，从而实现对电力营销与客户满意度指标体系科学性的评价，建立监督常态机制。文献[1-2]采用常规AHP(Analytic Hierachy Process)算法和模糊综合评价得出单一实数权重来对电力市场的供电服务品质综合指标进行评价，用这种单一实数矩阵定量描述定性指标隶属于某准则的比重，尽管思路简单，也能解决了对模糊事件的定量评价，粗略得出权重值，但必须是在满足一致性的前提下方能正确得出权重值对供电服务质量评价。它表明采用传统AHP算法对服务品质评价时具有其局限性。本文采用电力专家咨询数据，对得出的区间数判断矩阵进行优化处理，使得开始阶段就满足一致性直接求出权重值，而不需进行一致性检验，并且在本文的供电服务品质评价中还运用了极值点求解方法对拟优化一致矩阵的区间权重求解做了深入的研究，结果更具有全局最优性。这样不但克服了单一实数矩阵定量描述某一准则下的隶属比重的缺点，还对传统算法过程进行了优化处理。

冯延东（1964-），男，工程师，主要从事发电厂及变电站电气二次设计。