基于QR分解的低复杂度RLS算法研究

杨铁军，李军华

● （1．中国人民解放军92957部队，舟山 316001；2．海军工程大学，武汉 430033）

基于QR分解的低复杂度RLS算法研究

杨铁军1，李军华2

● （1．中国人民解放军92957部队，舟山 316001；2．海军工程大学，武汉 430033）

为避免RLS算法在迭代过程中的数值发散现象，研究了复数域下基于QR分解的RLS估计算法，推导了基于Givens旋转的免开方、免除法的逆QR-RLS算法，通过变换可直接得到滤波系数更新所需增益向量，避免了QR-RLS算法的回代运算，同时消除了逆QR-RLS算法在每次迭代时的N次开方、2N次除法运算，有效降低了运算量。

信道估计；RLS算法；QR分解；Givens旋转

0 引言

在短波数据通信系统中，为能够正确接收数据，需要对信道的统计特性进行估计。 信道估计技术的本质是实时提取信道的特征参数，用以支持数据检测。 为能够快速跟踪信道特性的变化，通常采用最小二乘方法进行信道估计。

RLS算法是一种自适应横向滤波器的递归算法，它的重要特点是收敛速率比一般 LMS滤波器快一个数量级，这是因为RLS滤波器通过利用数据相关矩阵的逆矩阵对输入数据进行白化处理。然而，RLS滤波器性能的改善是以复杂度的增加为代价，如何降低RLS算法的复杂度是其实用化的关键。

1 开方根自适应滤波器

1由于RLS算法中自相关矩阵R(n)及其逆矩阵P(n)是厄米特对称和正定的，当P(n)在递推过程中失去厄米特对称或正定的，RLS算法将是数值不稳定的。该不稳定性问题可采用开方根变形来改善[1]。开方根RLS算法在递归过程中传递的是由R(n)（或P(n)）定义的开方根下三角阵R1/2(n)（或P1/2(n)）。R(n)与R1/2(n)之间的关系为：

式中：RH/2(n) 为R1/2(n) 的厄米特转置。由于开方根RLS算法在递归过程中传递的是开方根矩阵 R1/2(n) 或P1/2(n)=R-1/2(n)，所以 R(n)=R1/2(n) RH/2(n)和 P(n)=P1/2(n)PH/2(n)确定的矩阵必定是厄米特型的，大多数情况下能保持它们的正定性。因此，这样的算法比标准的RLS算法有更好的数值特性[1]。

RLS算法中两个重要的开方根自适应滤波算法是基于QR分解的QR-RLS算法和逆QR-RLS算法。卡尔曼滤波器的开方根变形为这两种算法的导出提供了总体框架，这两种算法分别利用与卡尔曼开方根信息滤波器和开方根协方差滤波器的一一对应关系而得到[2]。基于QR分解的RLS算法是通过传递经QR分解后的开方根矩阵来完成最小二乘权向量的计算。QR-RLS算法和逆QR-RLS算法分别传递单个开方根R1/2(n)和P1/2(n)=R-1/2(n)。对于只要求先验误差 ξ(n)或后验误差 e(n)的应用情况，选择使用Givens旋转[2]的QR-RLS 算法更适用；而对于信道估计、均衡等要求抽头权矢量的应用情况，基于Givens旋转的逆QR-RLS算法更适合，这是因为逆QR-RLS算法可通过Givens旋转得到更新抽头的增益向量k(n)，而QR-RLS算法还需要通过回代的方法求解k(n)。因此本节重点讨论基于Givens旋转的逆QR-RLS算法。

1.1 逆QR-RLS算法

逆QR-RLS算法是基于对P1/2(n)=R-1/2(n)的Givens旋转变换得到的，每次迭代都可直接求得增益矢量k(n)，从而可通过递归方程更新抽头权向量。而QR-RLS算法在每次迭代后需要利用R-1/2(n)的下三角结构，通过回代的方法求解抽头权向量，因而逆QR-RLS算法在直接更新抽头权矢量时更有效。

就开方根而言，逆QR-RLS算法在递归过程中传递的是开方根矩阵P1/2(n)=R-1/2(n)，由卡尔曼滤波器与RLS算法变量之间的对应关系[2]，可以从卡尔曼开方根协方差滤波算法导出逆QR-RLS算法。逆QR-RLS算法通过Givens旋转来迭代更新增益矢量k(n)和开方根矩阵P1/2(n)。如式（2）所示，前阵列A是由P1/2(n-1)和当前时刻输入x(n)构成的(N+1)维方阵，通过Givens旋转变换，可在后阵列B中获得更新的开方根矩阵P1/2(n)和增益矢量k(n)。前后阵列变换关系为：

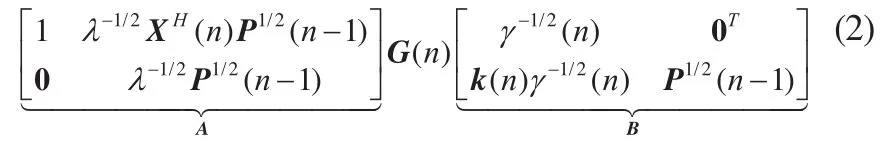
其中，P1/2(n)为上三角矩阵，0为N×1的零矢量，γ(n)为前面提到的收敛因子。G(n)为正交矩阵或酉旋转，它对前阵列中的块项λ-1/2XH(n)P1/2(n)进行运算，从而一一消其中的元素，并在后阵列第一行产生零块项。

利用矩阵分解引理[1]可得

将等式（3）两边矩阵相乘，比较矩阵两边对应项，可得，

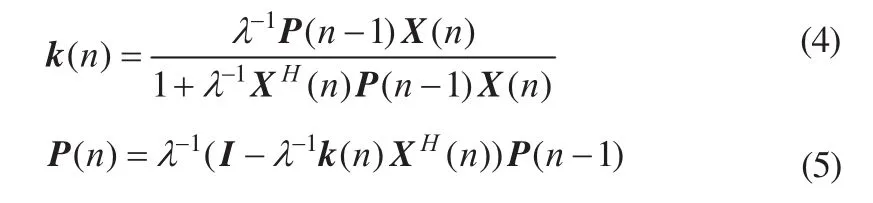
[1]知，逆QR-RLS算法与标准的RLS算法在递推过程中是等价的，它保留了标准RLS算法收敛速度快，以及对相关矩阵特征值扩散度变化不敏感等优点；同时，QR分解严格保证了矩阵P(n)在递归过程中的厄米特对称性和正定性。

(N+1)维的正交矩阵 G(n)用来对前矩阵A中第一行右边的N项进行N次Givens旋转，将第一行N个元素λ-1/2XH(n)P1/2(n)进行逐一置零，从而在后矩阵B中第一列产生与增益矢量k(n)相关的量，如式（2）。对应地，后矩阵中 P1/2(n)提供了需要更新前矩阵的量， 从而启动下一次迭代。因此，G(n)是 N个 Givens旋转的乘积，即G(n)=G(1)(n)·G(2)(n)……G(N)(n)。下面说明如何利用 N 个Givens旋转，依次消去块λ-1/2XH(n)P1/2(n-1)中的元素。需要注意的是，前矩阵中的 λ-1/2P1/2(n)为上三角矩阵，因此首先构造Givens旋转矩阵G(1)(n)，它对前矩阵的第一列和第二列起作用，使得第一行中第二个元素为零；依次类推，构造旋转矩阵G(i)(n)，它对前矩阵的第一列和第i +1列起作用，使得第一行中第i +1个元素为零，直到构造旋转矩阵G(N)(n)，它对前矩阵的第一列和最后一列作用，消去第一行中最后一个元素。Givens旋转矩阵G(i)(n)定义为(N+1)×(N+1)的方阵。

令 ρ(n)=[ρ1(n), ρ2(n),…ρN(n)]=λ-1/2XH(n)P1/2(n-1)为输入数据，单独抽出矩阵中需要更新的列，则第i次旋转为

由式（2）可知，b(0)(n) =1，b(N)(n) = γ-1/2(n)，u(0)(n) =[u(0)1(n)，u(0)2(n)，…，u(0)N(n)]T=0N，uN(n)=k(n)γ-1/2(n)。

将式（7）展开可得

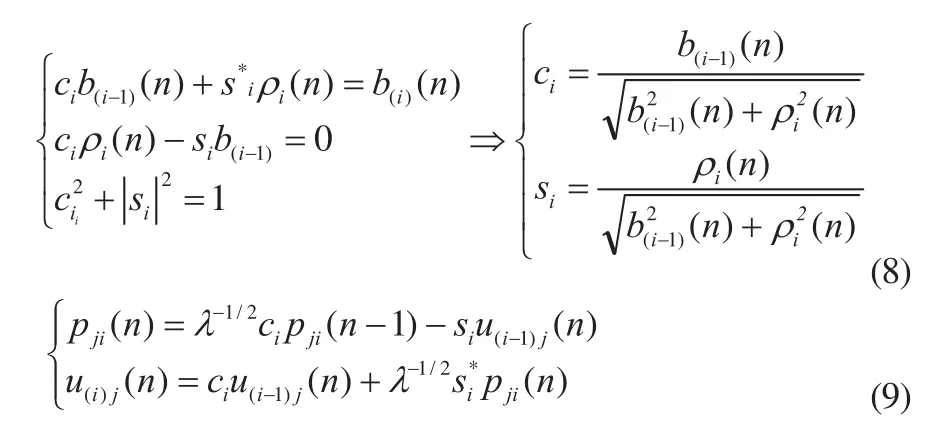
增益失量k(n)可由后矩阵的第一列求得

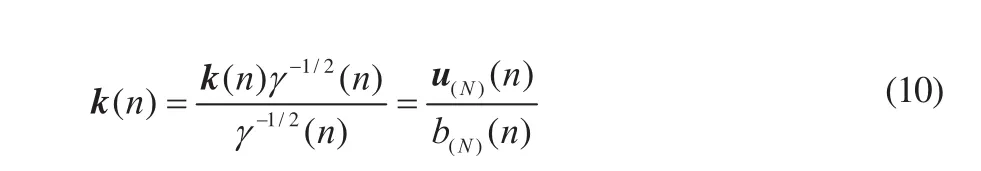
由式（8）可以看出，基于Givens旋转的逆QR-RLS算法在每输入一个数据都需要进行N次Givens旋转变换，也就需要N次开方和2N次除法运算。

1.2 低复杂度的逆QR-RLS算法

无论是基于QR分解的RLS算法还是逆QR分解的RLS算法，都需要进行开方和除法运算，基于Givens旋转的逆QR-RLS算法在每次输入数据时都需N次开方、2N次除法运算，在定点DSP和VLSI等实用化过程中，开方和除法运算所消耗的资源远远大于乘法和加减法，在高速实时数据传输中，其计算复杂度将成为数据处理的瓶颈。Frantzeskakis和Liu[3-5]等总结了各种免开方根QR RLS算法，通过变量代换，提出了一种基于Givens旋转的免开方、免除法的QR RLS算法框架。本节在此基础上，通过变量代换，推导了复数域下的免开方、免除法运算的逆QR-RLS算法，消除了每次迭代时的N次开方、2N次除法运算，为该算法的实用化铺平了道路。

令 ρ(n)=[ρ1(n), ρ2(n),…ρN(n)]=λ-1/2XH(n)P1/2(n)，β=λ-1/2，省略掉时间递推标号n，式（2）的N次Givens旋转可表示为

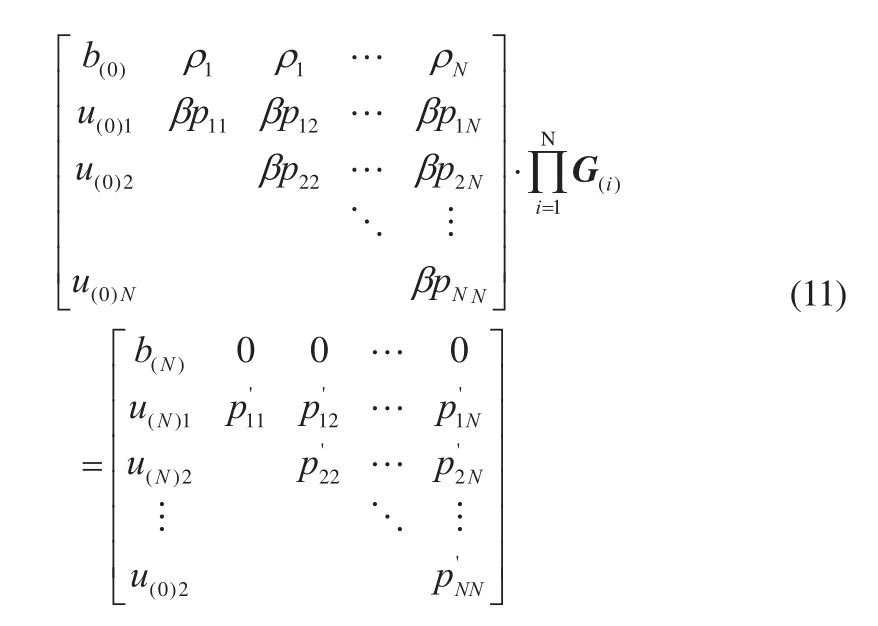
第i次Givens旋转为

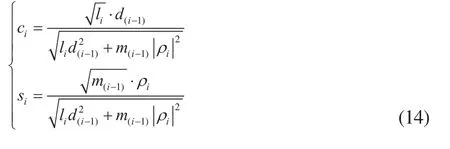
令上式中m(i)和分别为，

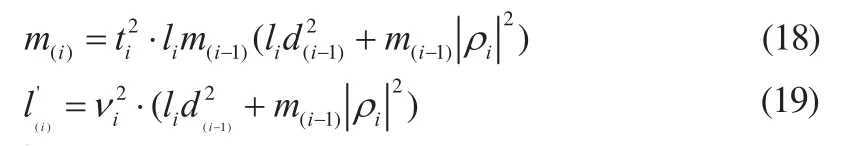
其中，ti, νi为正数。将式（18）、（19）分别代入式（15）、（16）、（17）中，则可消去其开方和除法运算，得

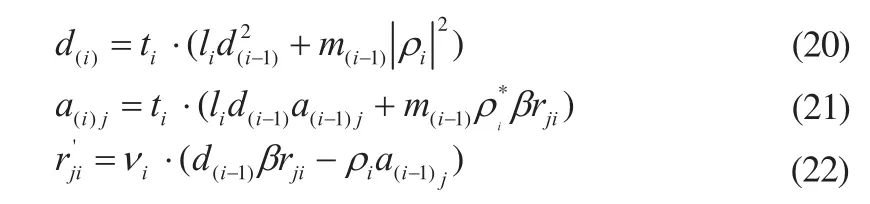
为了避免式（20）～（22）在迭代过程中数据的溢出，需要用参数ti, νi对其进行归一化处理。ti、νi的归一化处理通常采用2的幂次方，在定点处理器中只需进行移位操作。

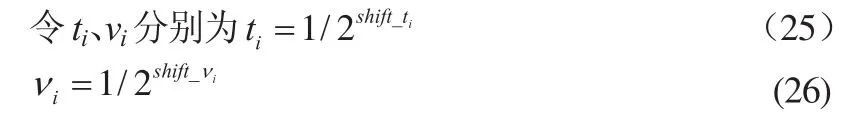
在迭代过程中只需对式（20）～（22）进行移位处理。

2 仿真分析

利用RLS算法、逆QR-RLS算法和免开方、免除法的逆 QR-RLS算法进行信道估计，信道模型选用文献[1]中的余弦脉冲响应，式（27）中取W=2.9。三种算法中遗忘因子λ=0.99，FIR 滤波器阶数为 11，SNR=30 dB，δ=10-4。

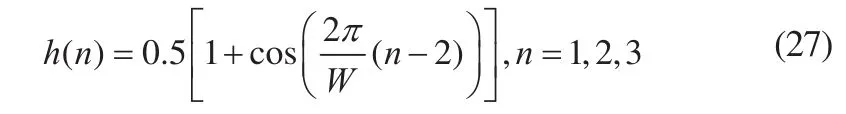
图1是100次集平均的MSE学习曲线。免开方、免除法的逆QR-RLS算法与逆QR-RLS算法和RLS算法具有相同的收敛特性和稳态误差，但前者不但克服了 RLS算法的数值发散现象，省掉了逆QR-RLS算法的N次开方、2N次除法运算，同时还可通过变换直接得到增益向量，避免了QR-RLS算法的回代运算，有效降低了运算量。

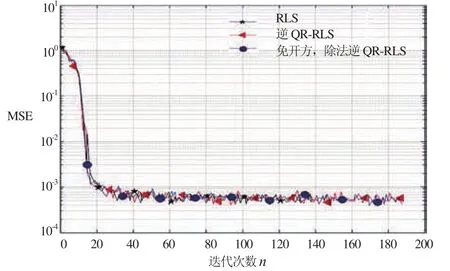
图1 不同RLS算法下的信道估计均方误差曲线

3 结语

由于RLS算法中自相关矩阵在迭代过程中会失去正定性，从而导致算法不稳定。为避免RLS算法在迭代过程中的数值发散现象，本文通过变换推导了基于 Givens旋转的免开方、免除法逆QR-RLS算法，避免了QR-RLS算法的回代运算，同时消除了逆QR-RLS算法在每次迭代时的N次开方、2N次除法运算。采用本文介绍算法可有效降低信道估计的复杂度，对于适时性高的场合具有一定的实用价值。

参考文献：

[1]Haykin S. Adaptive filter theory[M]. 北京：电子工业出版社, 2006.

[2]Manolakis D G. 统计与自适应信号处理[M]. 北京:机械工业出版社, 2003.

[3]Frantzeskakis E N, Liu K J R. A class of square root and division free algorithms and architectures for QRD-based adaptive signal processing[R]. Maryland:University of Maryland, institute for systems research center, college park, 1993.

[4]Frantzeskakis E N, Liu K J R. A class of square root and division free algorithms and architectures for QRD-based adaptive signal processing [J]. IEEE Trans.on Signal Processing, 1994, 42(9): 2455-2469.

[5]Realization of QR-RLS Adptive Equalization Algorithm with Low Complexity[J]. Journal of Wuhan University of Technology, 2010,1671:19-0153-06.

Low Complexity RLS Algorithm Based on QR Decomposition

YANG Tie-jun1, LI Jun-hua2
(1. 92957 Army of Chinese People's Liberation Army, Zhoushan 316001, China; 2. Naval Engineering University, Wuhan 430033,China)

To avoid the divergence problem encountering in RLS algorithm, the adaptive RLS filtering algorithm based on the QR decomposition over complex plane is analyzed. Then the Givens-based inverse QR-RLS algorithm, which wis a square-root-free and division-free scheme, is deduced in detail, which can overcome the divergence problem of RLS algorithm. Meanwhile, the square-root-free and division-free scheme can obtain the gain vector directly for coefficients-updated and save N square root and 2N division operations compared with inverse QR-RLS algorithm.

channel estimation; RLS algorithm; QR decomposition; Givens-based

TN911.5

A

杨铁军（1975-），男，高级工程师。研究方向：船机电监测。