三相全数字频率自适应闭环锁相技术
2013-10-17郭晓瑞郭吉丰龙英文
郭晓瑞,郭吉丰,龙英文
(1.浙江大学 电气工程学院,浙江 杭州 310027;2.合肥工业大学 光伏系统工程研究中心,安徽 合肥 230009)
0 引言
当前交流电源的供电方式正由集中式向分布式发展。在小型分布式发电系统中,存在着风能、太阳能、燃料电池、微型燃气轮机和储能系统等多种能源的组合供电,其大部分都需要通过逆变电源并联的形式接入微型公共电网[1-2]。为了使逆变器能够顺利并联运行,在实际系统中必须设计预同步过程,以确保逆变器在投入电网运行时其输出电流相位、频率与电网正序基波电压一致,从而减小对微电网以及逆变器本身的冲击。
实际电网中使用了越来越多的非线性负载,工业电网中的电压谐波含量及不平衡度都会受到影响[3-4],因此对于与电网相接的并网逆变器而言,快速精确地锁相非常重要,如果锁相不准确就会导致输出电网电流参考中含有大量的谐波[5]。锁相环(PLL)是目前使用最普遍的相位同步方法,它用于获得准确实时的相位信息,提供计算基准,其性能对于整个控制系统至关重要。在控制过程中要求锁相电路必须在存在电压畸变如谐波、频率突变、相位突变以及三相不平衡条件下,能够快速、准确地锁定电压相位,并需满足收敛速度快、相位估计精度高、抗干扰能力强等要求。对于在市电电压谐波含量非常大的情况下如何锁相已经展开了大量的研究,一般可以分为开环锁相方法[6-11]和闭环锁相方法[5,12-14]。文献[11]采用提取三相电压正序基波分量的开环锁相方法,该方法对于污染严重的市电有很好的锁相效果,但由于采用开环锁相,锁相精度有待提高。文献[5]采用提取三相市电电压正序基波分量的闭环锁相方法,但对电压正序基波分量滞后90°环节的全通滤波器环节没有自适应算法,电网频率变化时会出现较大锁相误差;另外采用的全通滤波器也不能很好地滤除谐波,电网电压畸变严重时锁相精度不高。文献[14]虽然解决了文献[5]涉及频率变动的不足,采用一种在线估算的带通滤波器取代全通滤波器,但计算方法复杂,不利于工程应用。
本文在分析三相同步旋转坐标变换原理的基础上,结合开环锁相方法和闭环锁相方法的优点,提出了一种新的全数字自适应闭环锁相方法,并详细分析了该锁相方法的工作原理。最后通过MATLAB的S-Function中的C语言编程,把本文提出的锁相新算法与文献[11]的开环锁相和文献[5]、[14]的闭环锁相进行比较,从仿真和实验结果可以看出,本文方法锁相精度好、谐波含量小、动态响应快,是具有工业应用前景的技术方案。
1 三相闭环锁相的基本原理
三相闭环锁相系统是一个相位误差反馈系统,由基于同步旋转坐标变换原理的数字鉴相器、低通滤波器(LPF)和压控振荡器组成,其基本工作原理是数字鉴相器将输入的三相电压信号和软件PLL内部同步信号的相位差转变成直流量,经过低通滤波器后去控制压控振荡器,从而调整系统内部信号的频率和相位,使之与输入电压的正序基波分量相位同步。同步旋转坐标变换实际上由从静止abc坐标系到αβ坐标系的变换和从αβ坐标系到dq旋转坐标系的变换组成。
三相市电正序基波分量通过2个变换矩阵就从三相静止坐标系变换到同步旋转坐标系:


其中,UA、UB、UC为市电三相电压,θp为市电正序基波相位。
式(1)简化为:

其中,Um为三相电压的幅值。
如果正序基波相位的给定参考值θp与实际反馈值θ相差不大,根据正弦函数特性可以认为下式成立:
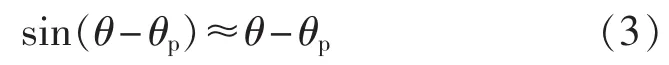
这样就可以通过PI控制器得到正序基波的相位,该锁相方法如图1所示。图中,ωc为PI控制器的输出信号,ωf为市电正序基波角频率前馈量,1/s为压控振荡器。
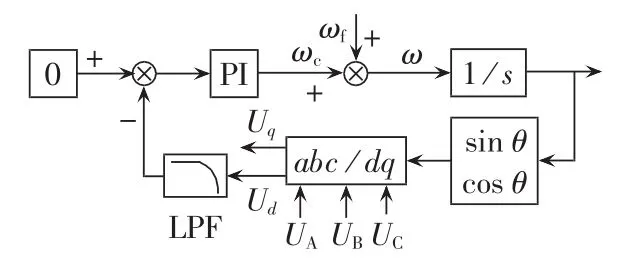
图1 三相闭环锁相框图Fig.1 Block diagram of three-phase PLL
从图1可以看出,在相位锁定的情况下三相电压信号中的正序基波分量在dq旋转坐标系下为直流量;负序基波分量与正序、负序谐波分量经过dq变换后均为高频交流分量。一般可以通过设计LPF将其滤除,从而达到锁定正序基波电压相位的目的。如果在三相市电电压负序和谐波含量比较高的情况下,要求LPF带宽非常低,才能尽可能滤除市电负序及高次谐波,但这样会影响锁相的追踪速度,这使LPF的设计难度非常大,因而传统的锁相方法很难满足设计要求。
2 改进的三相闭环锁相方法
含有谐波的三相电压UA、UB、UC可以表示为:
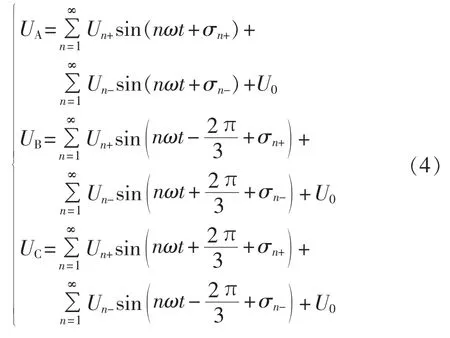
含有谐波的三相电压UA、UB、UC可以表示为:其中,U1+、U1-、Un+、Un-分别为三相市电正序基波、负序基波、n 次正序、n 次负序电压幅值;σ1+、σ1-、σn+、σn-分别为市电电压正序基波、负序基波、n次正序、n次负序分量初始相位角;ω为市电基波角频率;U0为市电电压零序分量。
如果市电污染严重,直接根据图1的方法进行锁相,必然会得到一个畸变的相位。所以首先要对三相市电电压采样信号进行处理,提取出不失真的正序基波分量。
三相市电正序分量可以通过下式的对称分量变换而得到[5]:
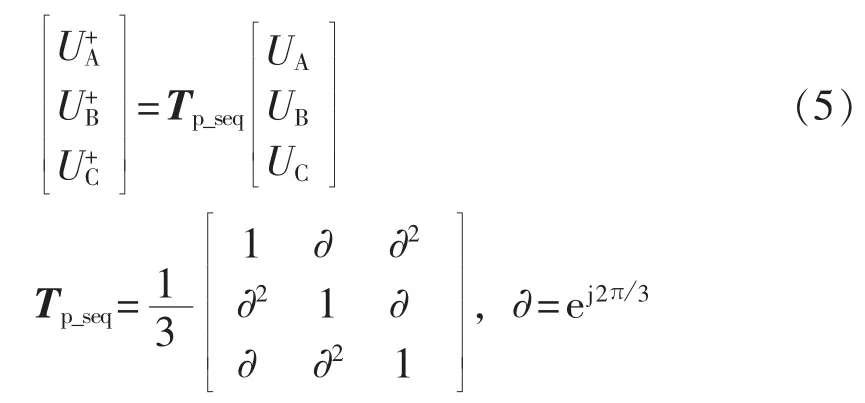
为了消除市电高次谐波的影响,把上式三相静止坐标系通过矩阵Tabc/αβ转化到两相αβ坐标系,可以得到三相市电正序分量在此坐标系下的表现形式:
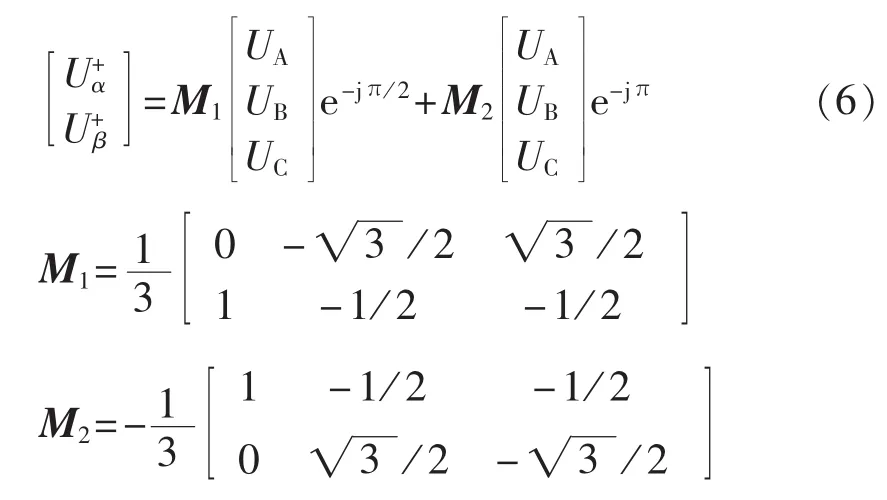
根据式(6)提取市电的正序基波分量,需要对输入电压采样信号中的基波分量不失真相移90°和180°的同时,也要对市电采样中的2次及以上谐波进行大幅度衰减,所以选取的LPF的截止频率设定为市电基波频率,且在市电基波频率点有90°相移,根据文献[11]推荐的二阶LPF可表示为:
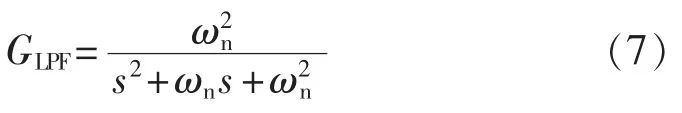
其中,ωn为市电电压正序基波角频率。
图2为LPF Bode图。可以看出,LPF对角频率略低于 ωn(ωn=100πrad/s)的信号幅值具有放大功能,对角频率高于ωn的信号具有衰减功能。LPF能将2次谐波衰减11.2 dB,3次谐波衰减18.7 dB,5次谐波衰减27.8 dB。对于相位需要滞后180°的要求,采用2个相同的LPF串联实现,对谐波的衰减幅度会更大。这样根据式(6)中的滞后90°和180°的环节可将三相市电电压采样信号中的高次谐波进行大幅度衰减,得到谐波含量比较低的αβ坐标系下的信号后再经过同步旋转坐标变换参与闭环锁相系统的反馈,就会使闭环锁相系统有效避免电压谐波的干扰,进一步提高锁相精度。
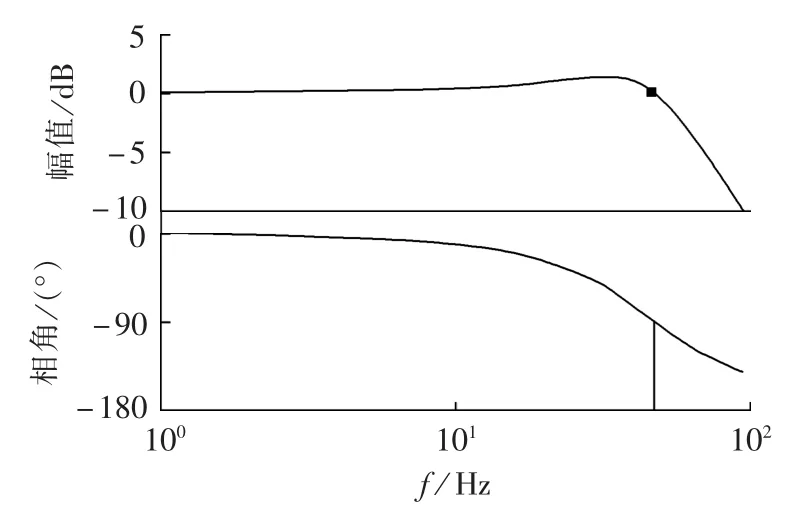
图2 LPF波特图Fig.2 Bode plot of LPF
3 频率自适应锁相算法
大多数国家都允许市电在一定频率范围内变动,二阶LPF中的自然角频率ωn也应随市电正序基波频率的改变而改变,加入频率自适应锁相算法能够保证市电正序基波频率在偏离50 Hz或60 Hz时的锁相精度。本文根据二阶LPF的特点来实现自适应锁相。设定闭环锁相通过查正弦表输出的正弦函数sin θ和余弦函数cos θ再经过一个相同的LPF滤波后分别为 λsin(θ-σ)和 λcos(θ-σ),其中 λ、σ 分别为幅值的变化量和相位的滞后量。对图2分析可以得知,如果LPF中的估算角频率正弦余弦信号会被衰减,λ<1;反之,如果正弦余弦信号被放大,λ>1。为了进一步放大误差信号,本文定义频率自适应的反馈函数为正弦余弦信号经LPF滤波后输出信号的平方和:


图3 频率自适应算法Fig.3 Frequency adaptation algorithm

改进后的三相全数字闭环锁相控制框图如图4所示。图中,LPF1为一阶LPF,其主要作用是进一步消除高次电压谐波分量,由于本文已经把输入的三相市电电压采样中的非正序基波分量大幅度衰减,为了保证闭环锁相的追踪速度,LPF1的带宽可以设计得高一些;k为比例系数,作用是把求取的市电正序基波角频率ω转换为数字锁相程序中列出的正弦表中的索引值,就可以方便地得到市电正序基波频率的 sin θ和 cos θ。k 定义为:

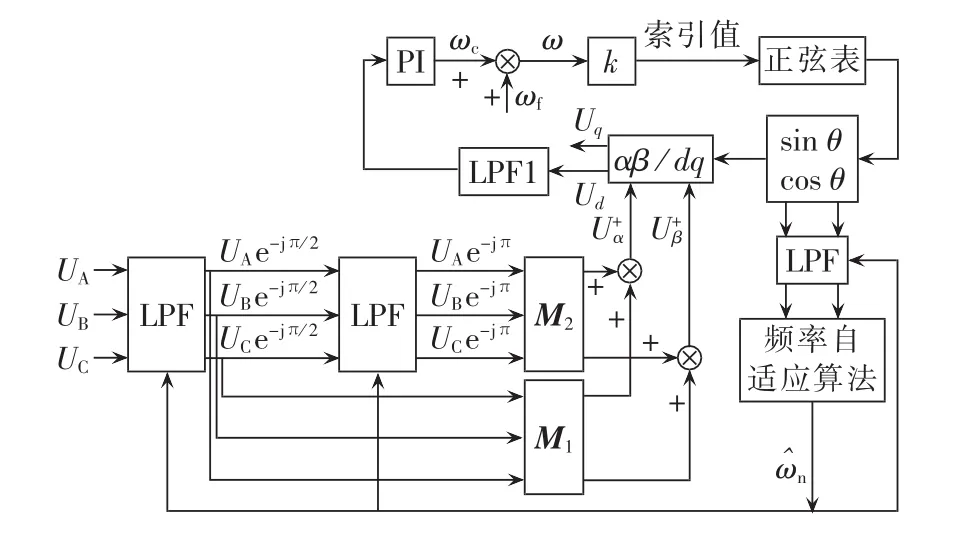
图4 改进后的三相全数字闭环锁相控制框图Fig.4 Block diagram of improved three-phase all-digital PLL control
其中,N为正弦表中表示0°~360°正弦函数的个数,Ts为数字控制中设定的采样周期。
设计实际的闭环锁相回路PI参数时,DSP采样和计算延迟e-τs环节是不能被忽略的,否则将出现理论设计与实际结果不符合的现象。纯滞后延迟环节会使控制系统的相角减小,从而降低系统的相位稳定裕度;另一方面如果控制系统响应速度变慢,系统相角裕度会增大,延迟环节的影响会被减弱,但锁相速度就会变差,所以需要折中考虑。设定DSP延迟时间为一个完整的采样周期。为了加快闭环锁相追踪速度,要求锁相环 PI(KP,KI)参数的设计可实现单位阶跃信号响应在5个采样周期内达到稳态。图5给出了不同的PI参数对应的单位阶跃响应曲线,图中,曲线1至5对应离散域中的PI参数分别为(1.8,0.003)、(0.9,0.002)、(1.1,0.006)、(0.5,0.002)和(0.3,0.001),其中曲线3对应的PI参数就是最终确定在仿真和实验中采用的参数。由于三相锁相环中闭环PI控制器和频率自适应积分控制器相互耦合在一起,为了降低耦合度,频率自适应积分控制器的带宽要远低于闭环PI锁相控制器的带宽,这就需要频率自适应积分控制器的计算间隔周期大于5个DSP采样周期的时间。为了加快市电频率变化时锁相追踪速度,同时考虑降低系统的耦合度,设定频率自适应积分控制器每间隔25个采样周期计算一次。
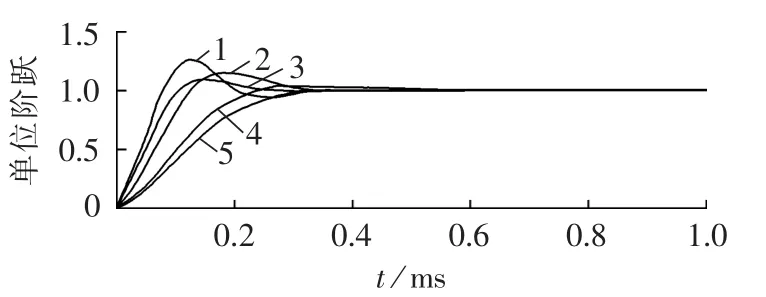
图5 单位阶跃响应曲线Fig.5 Response to unit step change for different PI parameters
4 仿真
为了验证本文提出的锁相算法具有较高的锁相精度,对文献[11]提出的开环锁相算法以及文献[5]和文献[14]提出的闭环锁相算法进行了仿真比较。其中采样周期 Ts=50×10-6s,N=720,k=0.00573,KI=1.2,GLPF1=850/(s+850)。
表13“方差方程的Levene检验”列方差齐次性检验结果:F值为0.0565,显著性概率为0.8200,大于0.05,因此两组方差不显著。
4.1 谐波分量仿真
三相系统中偶次谐波一般很小,所以只考虑奇次谐波。设定三相电网电压正序基波分量幅值为311 V,负序基波、3次零序谐波、5次负序谐波、7次正序谐波、9次零序谐波及11次负序谐波幅值为100 V。
在市电正序基波频率为50 Hz和52 Hz时分别采用不同的锁相方法,锁相输出的与市电电压正序基波分量同步的正弦信号的THD如表1所示。可以看出,本文提出的频率自适应锁相算法可以满足市电正序基波频率变化时的精度要求,并且在三相市电严重畸变时,本文提出的锁相算法的精度最高。
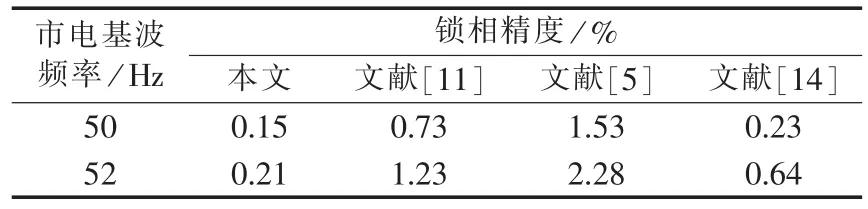
表1 采用不同算法时锁相输出同步信号的THD结果Tab.1 THD of synchronous output signal for different phase-locked methods
4.2 三相电压不平衡仿真
设定含有直流分量和负序基波分量的三相不平衡市电电压为:
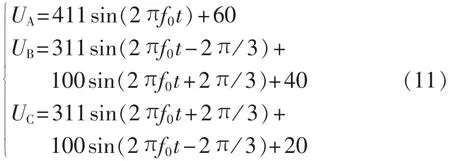
其中,f0为 50 Hz。
图6表示三相电压不平衡时锁相环输出的与市电电压正序基波分量幅值相等的正弦及余弦信号的仿真波形。图中,曲线1至5分别表示锁相环输出的正弦放大信号、余弦放大信号、A相市电电压、B相市电电压和C相市电电压波形。图7表示三相电压不平衡时市电A相电压正序基波分量及锁相环输出的同幅度正弦信号的相位对比仿真波形。图中,曲线1表示A相电压正序基波分量,曲线2表示锁相环输出的同幅度正弦信号。从图中可以看出,两者相位基本重合,锁相得到的正弦同步信号的THD为0.06%。同时采用文献[11]开环锁相、文献[5]闭环锁相及文献[14]闭环锁相得到的正弦同步信号的THD分别为0.21%、0.37%和0.17%。
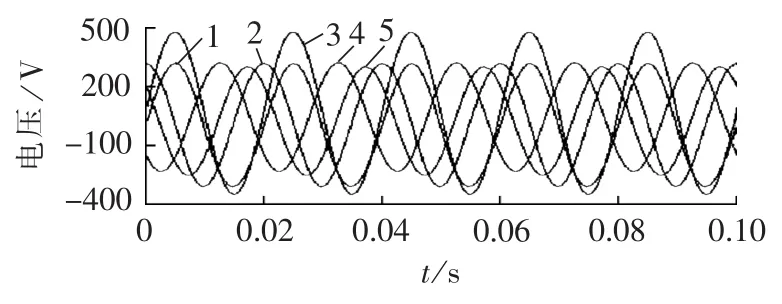
图6 三相不平衡市电及锁相输出仿真波形Fig.6 Unbalanced three-phase voltages and simulated waveforms of PLL output

图7 市电A相正序基波分量与锁相输出正弦信号相位比较Fig.7 Comparison of phase between positive-sequence fundamental component and output sine signal
4.3 频率及相位突变仿真
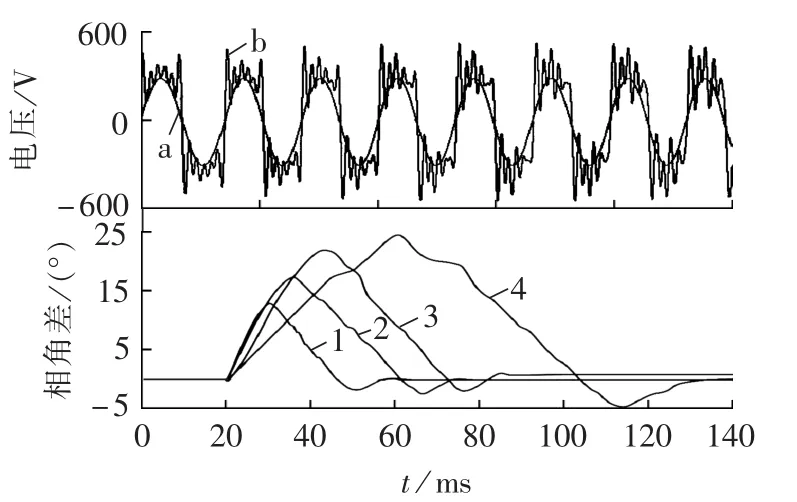
图8 市电基波频率突变5 Hz时不同算法仿真比较Fig.8 Simulative comparison among different algorithms for fundamental frequency abrupt change by 5 Hz
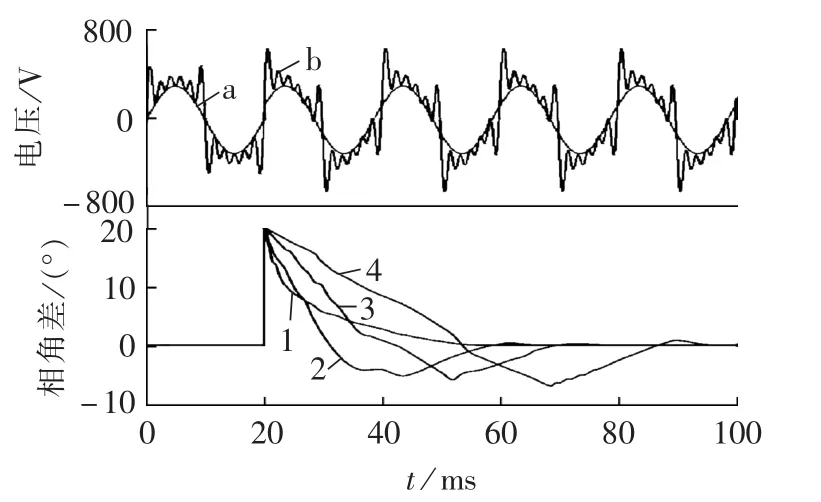
图9 市电基波相位突变20°时不同算法仿真比较Fig.9 Simulative comparison among different algorithms for fundamental phase abrupt change by 20°
图8表示三相市电正序基波频率在20 ms时从50 Hz突变到55 Hz时采用不同锁相方法的仿真对比波形,图9表示市电正序基波电压在20 ms时相角突变20°时采用不同锁相方法的仿真对比波形。图中,a表示市电正序基波电压分量,b表示污染市电波形,均为A相波形;曲线1至4分别表示采用本文提出的锁相方法、文献[11]开环频率自适应锁相、文献[5]和文献[14]闭环锁相仿真得到的瞬时相角误差变化曲线。可以看出,当三相市电正序基波频率变化或相角突变时,本文提出的频率自适应锁相方法追踪速度最快。
5 实验结果
为了检验本文提出的三相全数字闭环自适应锁相的效果,采用DSP 32位定点计算的TMS320F2812,设定采样及计算频率都为20 kHz,实验具体参数与上述仿真完全一致。其中三相电网电压正序基波分量幅值为311 V,负序基波、3次、5次、7次、9次及11次谐波幅值为100 V。
图10为A相污染市电电压、正序基波分量与锁相输出波形。图中,曲线1为A相污染市电电压波形,曲线2为A相电压的正序基波分量,曲线3为DSP控制板D/A输出最大电压3.3 V锁相信号的放大波形,稳态时锁相输出波形的THD为0.19%,曲线3和曲线2的相位差的余弦值为0.9992。
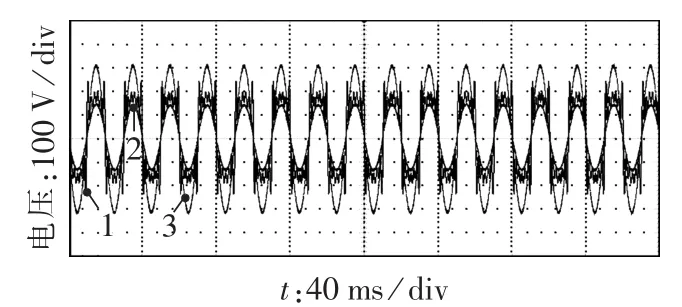
图10 污染市电电压、正序基波分量与锁相输出波形(A相)Fig.10 Waveforms of polluted line voltage,positive-sequence fundamental component and PLL output voltage(phase A)
图11表示DSP开始工作时锁相追踪基波频率为50 Hz三相污染市电的瞬态波形。图中,曲线1为A相污染市电电压波形,曲线2为A相电压的正序基波分量,曲线3为DSP控制板D/A输出锁相信号的放大波形。为了更好地体现追踪速度,DSP程序中设定正弦表索引初始值从90°相位开始追踪。可以看出,大概需要15 ms就可以完全追踪市电正序基波电压的相位。

图11 锁相追踪基波频率为50 Hz污染电压的瞬态波形Fig.11 Dynamic waveforms of PLL tracking for polluted line voltage at 50 Hz
图12表示DSP开始工作时频率自适应锁相算法追踪基波频率为55 Hz三相污染市电的瞬态波形,曲线含义同图11。同样为了更好地体现追踪速度,DSP程序中设定正弦表索引初始值从90°相位开始追踪,数字锁相程序中设定的初始估算角频率n为100π。可以看出,大概需要40 ms就可以完全追踪55 Hz的市电正序基波电压的相位。

图12 自适应锁相追踪基波频率突变为55 Hz污染电压的瞬态波形Fig.12 Dynamic waveforms of frequency-adaptive PLL tracking for polluted line voltage changing to 55 Hz
6 结论
本文结合开环锁相和闭环锁相的优点,提出了一种三相全数字频率自适应锁相新算法。该算法能够快速准确追踪市电电压正序基波分量的相位、频率,保证了算法的实用性。在此基础上,实现了对三相电网电压频率的自适应跟踪,减少了频谱泄漏,提高了基波同步参数检测的精度。相对于传统的开环和闭环锁相方法,在谐波和零点漂移严重的情况下,该算法仍然可以精确跟踪电网电压基波正序分量,从而减小并网逆变器对微电网以及逆变器本身的冲击。最后,仿真及实验结果验证了该锁相算法的正确性。
