基于解耦后输电线路纵向阻抗的改进型纵联保护
2013-10-17夏经德索南加乐张怿宁邵文权何世恩
夏经德 ,索南加乐 ,张怿宁 ,3,王 斌 ,邵文权 ,何世恩 ,4
(1.西安工程大学 电子信息学院,陕西 西安 710048;2.西安交通大学 电气工程学院,陕西 西安 710049;3.中国南方电网超高压输电公司 检修试验中心,广东 广州 510663;4.甘肃省电力公司,甘肃 兰州 730050)
0 引言
随着微机控制技术[1]、光纤通信技术[2]和电子传感技术[3-4]的快速发展,输电线路纵联保护的性能也将得到大幅的提升[5]。在传统的纵联保护中,虽然电流差动保护可成功地提取出最能反映故障特征的故障电流来获得稳定可靠的甄别效果[6],但是需要线路各端同步采样电流数据,同时受线路分布电容的影响较大,并且在单侧电源下将丧失绝大部分故障判别的灵敏度[7];方向比较纵联保护简单可靠,只需要相对低廉的数据通信量[8-9],并且不需要两端同步采样,可达到较快的动作速度,但在分相保护中需配置选相元件,保护的灵敏度不高,在单侧电源下不能可靠工作,在大电源侧存在电压死区的缺陷[10-11]。因为三相线路模型存在相间耦合的影响[12-13],在继电保护的性能分析中往往通过单相模型建立数学定义和分析结论,然后将这个成果推广运用到三相模型并且建立合理的保护算法,形成满足要求的动作判据。
纵向阻抗(LI)有效利用了零序电压和零序电流的等效转换关系,达到了消除相间耦合,简化电路结构和明晰阻抗计算的目的,可以直接在三相模型下推导出准确的计算形式,相比文献[11],它可以获得更稳定、可靠的阻抗模型和判别效果;同时,这种解耦算法具有比距离阻抗保护更合理的消耦效应和更准确的判别结果。
文献[14]没有考虑系统阻抗和线路电容对阻抗的影响。本文通过理论分析后发现,当系统阻抗大于一定限值后将会严重威胁LI结果的可靠性。在分析系统短路容量特征的基础上增加了线路各端测量阻抗的辅助判据。根据分析可知,在已有系统和线路的各种运行方式下,所增加的辅助判据能够和LI主判据构成完美的配合。
1 单相模型的阻抗特性
图1分别是在区外和区内故障时R-L单相等效工频故障分量线路模型。
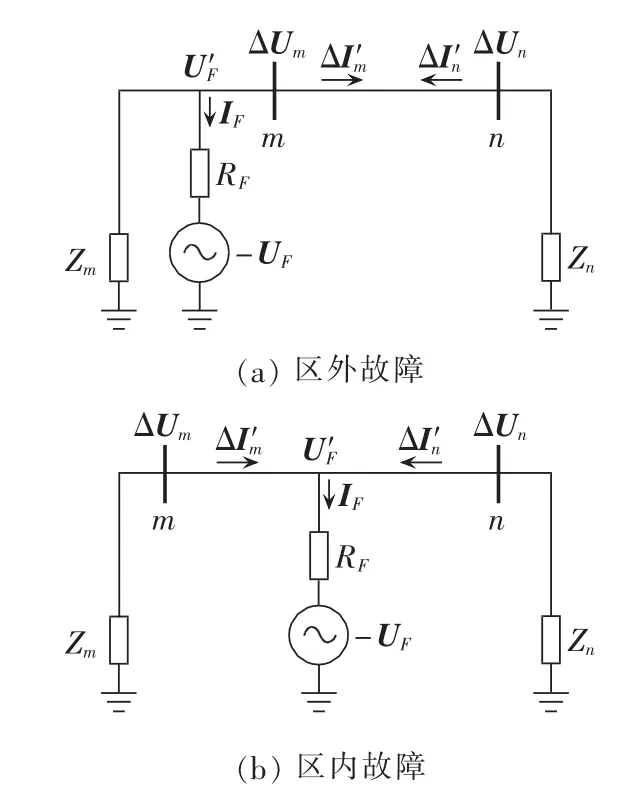
图1 R-L单相等效线路模型Fig.1 R-L single-phase equivalent line model
在图1中,m和n分别为被保护线路的两侧电气测量端,被保护线路全长为D;Zm和Zn分别为线路两侧系统阻抗;单位长度线路阻抗为z;内部故障时从m端到故障点测算获得的故障距离为d;RF为故障电阻;-UF和IF为故障点等效工频电动势和故障电流;U′F为线路故障点处实际工频电压;ΔUm和ΔUn分别为在线路两端测量得到的工频电压故障分量;ΔI′m和 ΔI′n分别为在线路两端测量得到的工频电流故障分量(不考虑线路电容的影响)。工频电流故障分量的设定流向已在图中标出。
1.1 单相模型下LI的定义[14]
在文献[14]的基础上,结合图1所示线路逻辑关系,定义LI如下:
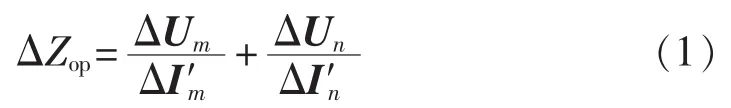
1.2 区外故障[14]
将两端电压差除以任意一端电流,可以得到:

同样,图1(a)所示的两端电流相量和的结果是ΔI′m+ΔI′n=0,因此,式(2)可以转换为:

上述结果意味着可将本端测量阻抗ΔUm/ΔI′m传送到对端,再和对端测量阻抗ΔUn/ΔI′n进行相量和运算,从而得出LI在区外故障时的结果。由式(3)可知,当区外故障时,LI为线路阻抗。
众所周知,在方向比较纵联保护中存在电压死区的缺陷,实际可反映为当遇到大电源时,其电压故障分量的幅值较小,在极端状态下甚至趋于零,由此将影响电压和电流间相位差数值的稳定提取,降低甚至威胁其可靠性。
由式(3)的结构可以看出,LI将线路两端的测量阻抗依据线路阻抗联系起来,形成了互补的关联,完全可以抵御单端电压过小所带来的影响。
1.3 区内故障[14]
如图1(b)所示,在区内故障时,线路各端的电压和电流故障分量的关系可分别表示为:
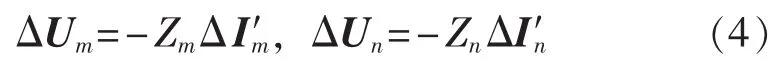
式(4)中线路各端电压除以相同端电流,将结果代入式(3)中,可以得到:
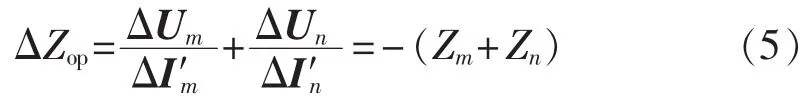
由式(5)可知,当区内故障时,上述LI为区外系统阻抗相量和的负值。由式(3)和式(5)的对比可以看出,由于在区外故障时LI就是线路阻抗,它非常明确,当LI偏离线路阻抗时就可以断定为区内故障。这样,可以将LI偏离线路阻抗的程度作为故障类型识别的依据。
根据式(5)的计算形式可以看出,LI将两端的测量阻抗联系起来,构成一个合理的数据关系链,完全可以避免单侧电气量扰动所带来的任何相关影响,所得结果和线路阻抗形成了反相的相量关系,状态的分辨裕度更宽,因此相比方向比较纵联保护,它的可靠性也更高。
由此可以看出,当发生区内故障时,所得阻抗为系统阻抗负的相量和,式(3)和式(5)之间的差异就是LI确认故障状态的依据。
2 三相模型的阻抗特性
图2是a相单相接地故障的R-L三相等效工频故障分量模型,图3是零序等效工频线路模型。
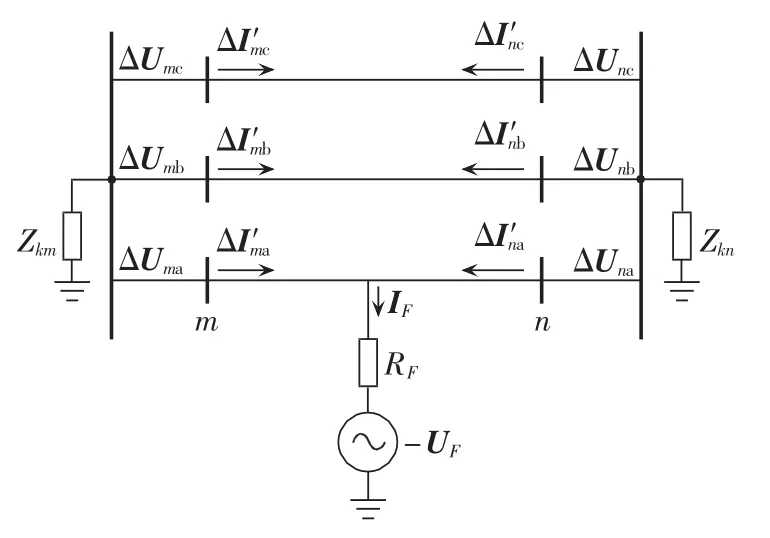
图2 R-L三相等效线路模型Fig.2 R-L three-phase equivalent line model
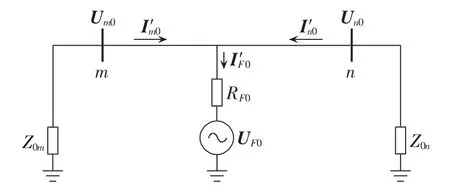
图3 R-L零序线路等效模型Fig.3 R-L zero-sequence equivalent line model
在图 2、3 中,Zkm、Zkn在下标 k 取 s、m、1 和 0 时分别为线路两侧系统自阻抗、互阻抗、正序阻抗和零序阻抗;zs、zm、z1、z0分别为单位长度线路的自阻抗、互阻抗、正序阻抗和零序阻抗;RF0为零序故障电阻;-UF0和IF0是故障点零序等效工频电动势和零序故障电流;ΔUmφ和 ΔUnφ(φ=a,b,c)分别为线路两端测量所得的各相工频电压故障分量;ΔI′mφ和 ΔI′nφ(φ=a,b,c)分别为线路两端测量所得的各相工频电流故障分量(不考虑线路电容的影响);Um0和Un0分别为线路两端工频零序电压;I′m0和 I′n0分别为线路两端工频零序电流(不考虑线路电容的影响)。各电流故障分量的设定方向已在图2和图3上标出。
2.1 三相模型下LI的定义
根据单相模型的分析结果,结合图2所示三相模型,定义三相模型基于故障分量的任意相LI为各端经精确解耦后的各相电压除以相同端同相电流相量,具体计算形式为:
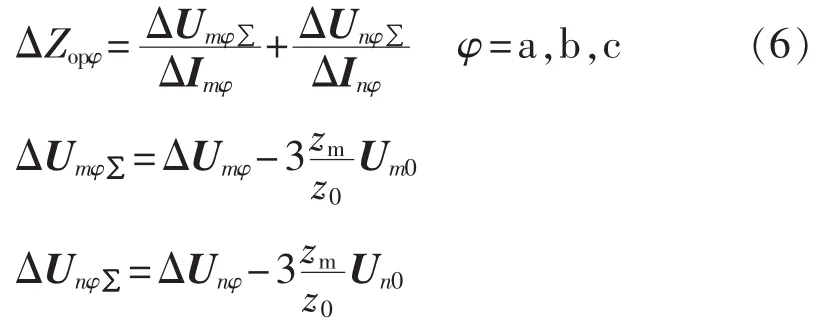
首先建立LI的基本状态表达关系。按照图2所示,各相两端电压相量差可表示为:
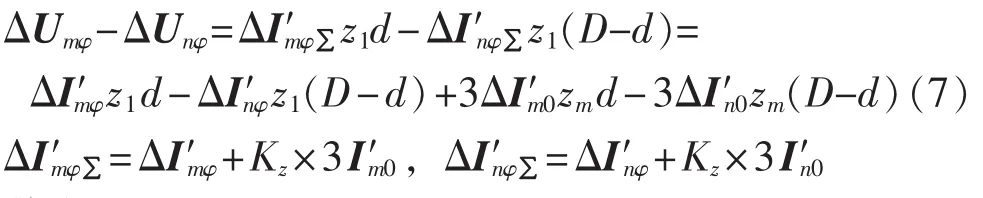
其中,Kz=(z0-z1)/(3z1)。
按照图3所示,两端零序电压相量差可表示为:
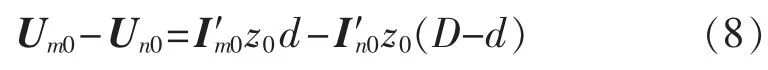
将式(7)的零序电流用式(8)的零序电压进行等效替换,经移项整理并除以相同相任意一端的电流故障分量后,式(7)可以表示为:
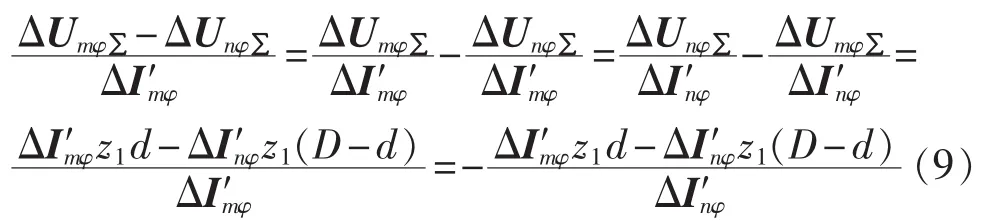
2.2 健全相
针对图2所示三相模型的健全相b相和c相,可以分别得到这2个健全相两端电流相量和为:
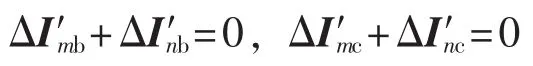
因此,式(7)可以转换为:
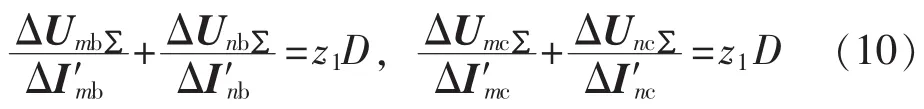
由此可以看出,上述解耦算法能够彻底消除相间耦合的影响,使得式(10)和式(3)的计算形式完全一致,并且将基于单相模型的LI(等于线路阻抗)准确地换算为基于三相模型的线路正序阻抗。
2.3 故障相
针对图2所示三相等效线路模型的故障相a相,可以得到该相按照两端电流和电压用区外系统阻抗所表示的关系为:
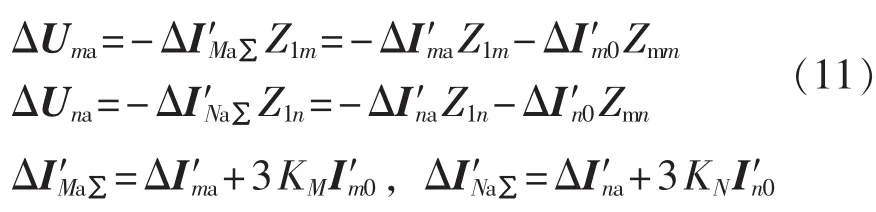
其中,KM=Zmm/Z1m,KN=Zmn/Z1n。
同样,按图3所示,可得零序电压和零序电流基于区外零序系统阻抗所表示的等式关系为:
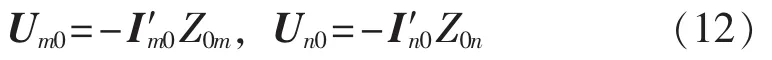
将式(11)的零序电流用式(12)的零序电压等效替换,经移项整理并除以相同端该相电流后,式(11)可以表示为:

当使用式(6)表示式(13)时,可以得到:

其中,Z′1m和Z′1n分别为基于三相参数和外部参数导出的两侧等效系统正序阻抗。
根据式(14)可以看出,计算出的等效正序系统阻抗明显不同于实际的正序系统阻抗。根据实际线路和系统参数的特点可知,由于在超/特高压输电线路中,所有相关阻抗的相角都非常趋近于90°,因此计算带来的偏差对于等效系统阻抗而言主要反映在阻抗的幅值上,而其相角的偏差不大,不会改变其所呈现的基本阻抗特征。
基于式(14),当区内故障时,LI等于等效系统正序阻抗负的相量和。LI能够有效消减相间耦合的影响,并对于区外故障获得明显可信度。这个结果能确保与1.1节和1.2节的结果保持一致。实际上,当区内故障发生时,虽然计算结果出现了一定的偏差,但依据电力系统的运行分析和特性统计,这个偏差实际非常有限,并且完全可以被工程计算和故障识别所接受。精确解耦后的LI可用图4表示。
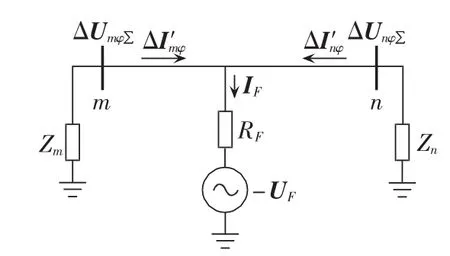
图4 R-L单相解耦线路模型Fig.4 R-L single-phase decoupled line model
由此可知,通过设置的精确解耦算法,LI相比方向比较纵联保护,具有自选相跳闸的能力。
3 性能分析
3.1 解耦算法的性能特点
在基于阻抗特性继电保护的分析中,相间耦合的影响是不容回避的。文献[14]虽然确立了LI的许多重要特性,但是由于未能消除相间耦合的影响,大幅削弱了其实用价值。本文所做的工作之一就是弥补了上述缺陷。
在距离阻抗保护中,已经建立起完善的补偿算法,可以有效减免相间耦合的影响[15]。本文所提的解耦算法与补偿算法相比具有非常明显的优势。
首先回顾距离阻抗的补偿算法,针对故障相,在忽略故障电阻的情况下,距离阻抗的幅值与故障距离呈现绝对的线性关系;但是在考虑故障电阻存在的情况下,距离阻抗将受到故障电阻及对端系统双重因素的影响,性能由此急剧恶化。根据式(5)和式(14)所示,LI根本不包含故障电阻的因素,因此故障电阻影响不到LI,系统运行方式不仅不会影响LI,而且成为LI状态识别的重要性能标志。
针对健全相,距离阻抗的补偿算法不仅不能有效消减相间耦合,实际上还需要增加一个小于1的修正系数来减免由于过补偿所带来的不利影响,因此它的补偿效果非常有限。LI的解耦算法从原理上完全消除相间耦合的影响,因此其结果可以准确表示为线路的正序阻抗。
由此可知,解耦算法比补偿算法更可靠灵敏。
3.2 不同步采样下的阻抗特点
在输电线路纵联保护中,需要线路各端同步调时。在各输电线路纵联保护的方式中,电流差动保护就必须保证各端电流保持严格的同步采样。
LI从原理上可以确定只需将本端的测量阻抗发送到对端,就可以满足需要,完全不涉及两端电压和电流同步采样及其相关的技术问题,因此LI完全可以不考虑各电气量的同步采样。
3.3 系统运行方式下的阻抗特点
线路在运行时可能遇到强系统向另一侧弱系统甚至是无源系统供电,导致弱系统阻抗较正常运行情况大,在极端情况下会面临系统阻抗趋于无穷大的情况。这里假设可能出现由此,LI将呈如式(15)所示变化。
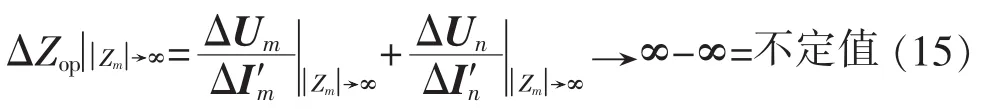
由式(15)可以看出,当系统阻抗较大时,会引发LI计算结果的不可靠,在此情况下不能保证在区外故障时LI等于线路阻抗。LI在取得不需考虑同步采样优势的同时,降低了阻抗计算的可靠性,这个缺陷需要规避。
在输电线路运行中,线路至少有一侧的系统为电源端。根据运行要求,该侧系统的短路容量必须数倍于该线路的自然传输功率,才能保证电力的正常输送;而且根据统计,此倍数至少要大于5。系统的短路容量可以等效反映为系统阻抗,而输电线路的自然传输功率可以等效反映为线路的特征阻抗,因此上述的功率比值关系可以等效转换为系统阻抗和特征阻抗的比较。动模所用750 kV输电线路,它的特征阻抗约为250 Ω。这样,当线路两侧的测量阻抗都明显大于50 Ω时,就可以确认没有任何一侧的系统为电源端,由此违反了上述电力系统运行设定的条件,可以确认此为区外故障。然而根据LI的计算特点,当发生区外故障、电源侧系统阻抗满足此设定条件时,仍然需要校验LI是否稳定、可靠。
首先,在增加线路分布电容影响的基础上,定性分析系统阻抗与LI在线路Π型等效模型下的对应关系。图5所示为当发生区外故障时带等效并联电容的Π型单相等效工频故障分量模型,图中,ΔImφ、ΔInφ分别为线路两端测量所得的各相工频电流故障分量(包含了线路电容的影响);线路单位长度电容为c;ΔImC和ΔInC分别为线路两端的等效电容电流。
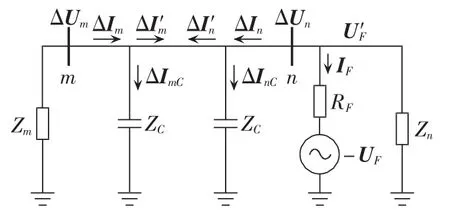
图5 Π型单相等效线路模型Fig.5 Π-type single-phase equivalent line model
按照图5所示,m端的测量阻抗就是m端区外的系统阻抗Zm,而n端的测量阻抗可表示为:
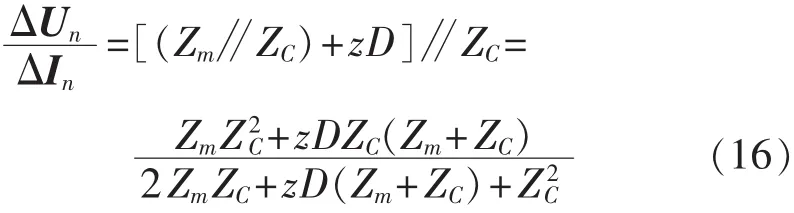
当系统阻抗Zm为纯电阻时,和线路左侧等效电容并联后,表示为较并联前标幺值缩小的电阻和电容的串联,并且其等效阻抗将抵消线路感抗,使对端(n端)的测量阻抗呈现缩小的趋势,LI变小;当Zm为感抗时,和线路左侧电容并联后为较并联前放大的感抗(当系统阻抗幅值小于线路特征阻抗时),并且其等效阻抗将放大线路感抗,使对端测量阻抗呈现放大的趋势,LI变大。
因为当发生区外故障时,LI的结果与线路阻抗直接相关,因此可以先假设存在如下对应关系:
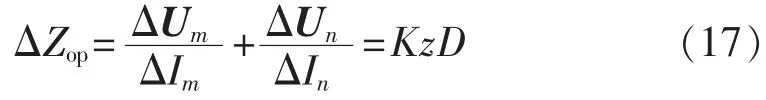
其中,K为一个任意随机的实数。
将m侧测量阻抗(依据式(4)转换等效获得)和n 侧测量阻抗(式(16))代入式(17),对式(17)进行恒等转换,并且设转换后的分子项为零,可以获得以下计算关系:
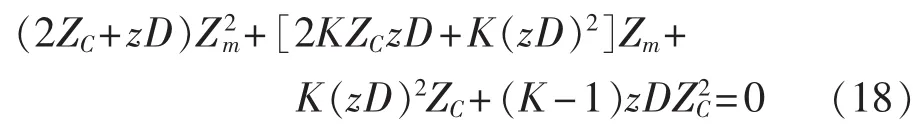
取LI保护动作主判据式(21)的下限K=KQS1=0.5,并且代入文献[16]所用 1000 kV、500 km 输电线路的相关参数,计算所得对应的系统阻抗为:
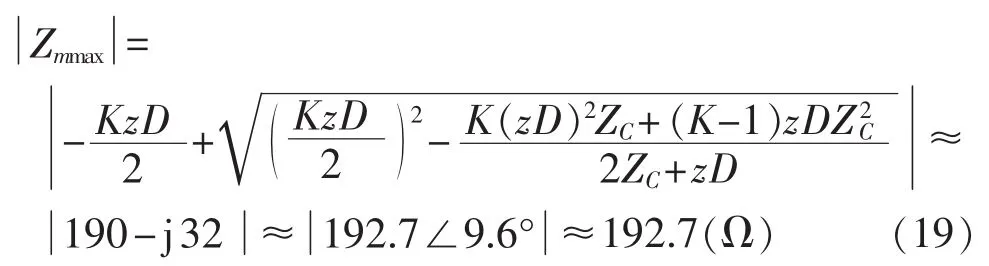
同样取LI保护动作判据式(21)的上限K=KQS2=2.0,对应的系统阻抗为:
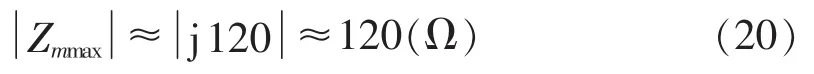
根据以上结果的对比可以获得如下结论:
a.只要系统阻抗的幅值小于50 Ω,在区外故障时,LI的阻值就能够确保限制在线路阻抗附近,由此可以保证LI的稳定性和其保护的可靠性;
b.当发生区内故障时,至少有一侧系统为电源端,其系统阻抗必然小于50 Ω,因此也就能够处于式(21)所设定辅助判据的最大限制范围内;
c.虽然解耦算法式(14)调整了系统阻抗的幅值,但是其调整的变化量是非常有限的,根据各种实际线路和系统运行参数统计可知,调整后的阻抗幅值绝对不会超越式(21)所设限制值;
d.只要线路两端测量阻抗的幅值都大于式(21)辅助判据所设定的最大限值,就能够认定没有任何一端的测量阻抗反映为电源端的等效系统阻抗,违反了上述所设的要求,由此可以不必进行LI的计算,直接判定为区外故障;
e.增加测量阻抗幅值的辅助判据能够可靠辅助LI的主判据,构成完整可靠的纵联保护。
4 各种纵联保护的性能比较
传统的输电线路纵联保护包括电流差动保护、方向比较纵联保护和阻抗纵联保护等。本文提出了基于LI的新型输电线路纵联保护。上述各种纵联保护的性能对比如表1所示。
由表1可以看出,传统的输电线路纵联保护在所列的性能状态及动作特点等方面存在一些明显的限制或者缺陷,如电流差动保护需要同步采样各端的电流,这些限制或者缺陷将影响其实际使用效果;LI虽然在数据传输量上不具有优势,但是通过其他性能的提高,完全可以弥补对通信信道的苛求。由于该阻抗所拥有的独特特点,在未来的纵联保护中具有较好的推广价值和运用前景。

表1 各纵联保护的性能对比Tab.1 Comparison of performance among various pilot protections
5 基于LI的纵联保护
根据上述的内容分析,在此提出了基于分相精确解耦算法故障分量LI的输电线路纵联保护。该纵联保护有3组计算元件,分别是纵联保护启动元件、线路各侧测量阻抗判别元件和故障分量LI的计算元件,这3组计算元件之间通过与运算联合,具体如式(21)所示。
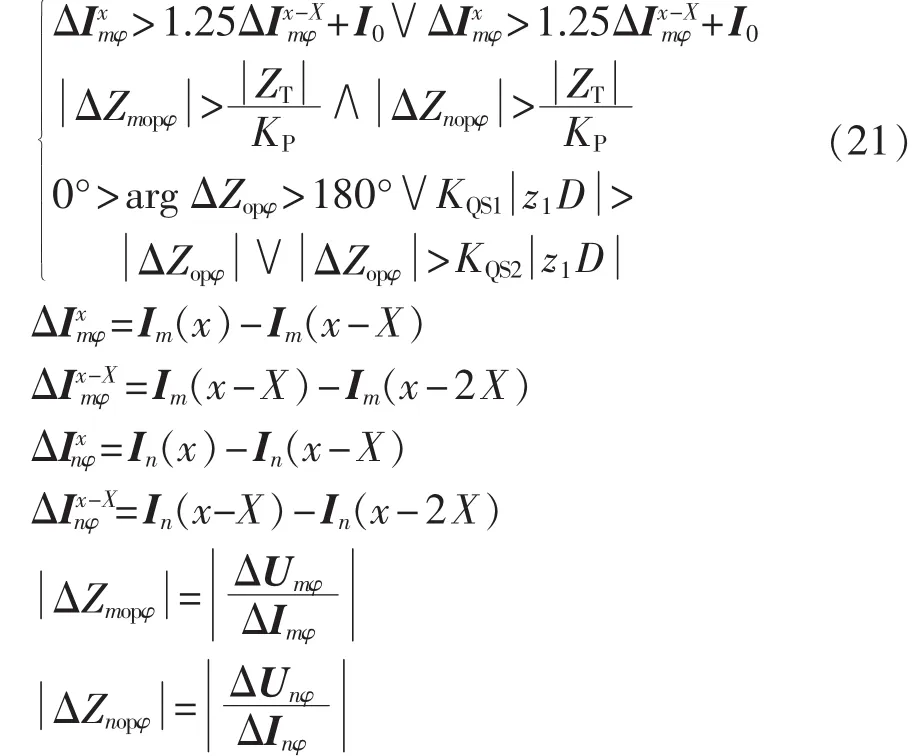
6 动模仿真验证
在本文所示动模仿真中,系统的额定电压为750 kV。
6.1 动模仿真模型及结果
在兰州东至咸阳的继电保护动模试验系统中,建立了750 kV输电线路模型,整个系统是由中国电力科学研究院牵头,将实际输电系统通过实验室以真实的器件构建的缩小模型,其中输电线路部分是由真实器件构建的小模型串联而成的。其中,输电线路的主要参数为:D=497 km,z1D=133.34∠87°Ω,r1=0.01217 Ω /km,r0=0.2729 Ω /km,l1=0.8531 mH/km,l0=2.674mH/km,c1=0.0137μF/km,c0=0.0093μF/km。
在线路中,对所发生各种类型故障其故障电阻的设置值为:金属性故障,RF=1.0×10-5Ω;单相高阻接地故障,RF=400 Ω;相间高阻短路和两相高阻接地故障,RF=100 Ω。在动模系统中主要发电机的参数见表 2为标幺值。
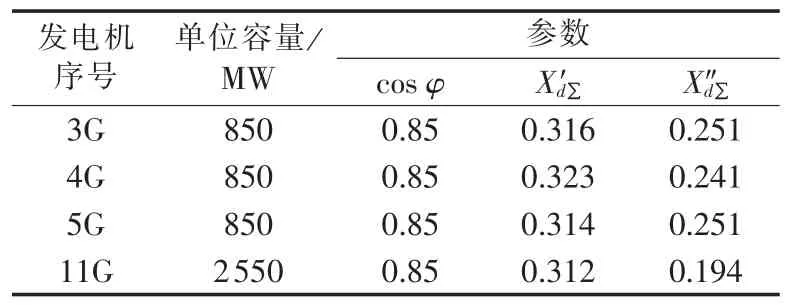
表2 动模系统主要发电机参数Tab.2 Main generator parameters of dynamic emulation system
系统接线图见图6,图中1号、2号和3号并联电抗器的容量分别为3×100 Mvar,4号并联电抗器的容量为3×90 Mvar。故障位置k10、k11和k12位于被保护区内,k13位于被保护区外。
表3—5为动模仿真的验证结果。

图6 兰州东—咸阳动模试验故障位置示意图Fig.6 Fault positions for dynamic emulation test of East Lanzhou-Xianyang
6.2 结果分析
从表3—5所示仿真结果可获得以下结论。
a.对于外部故障,所有的LI都反映为被保护线路的正序阻抗,能确保纵联保护的可靠性。
b.对于内部故障,它们都趋向于系统阻抗负的相量和,同样可确保纵联保护的灵敏性。
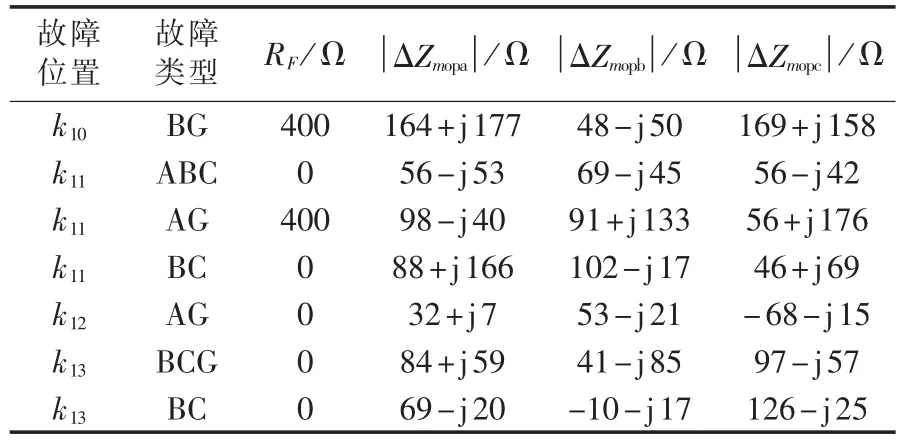
表3 m侧动模仿真的验证结果Tab.3 Verification results of dynamic emulation test at m side
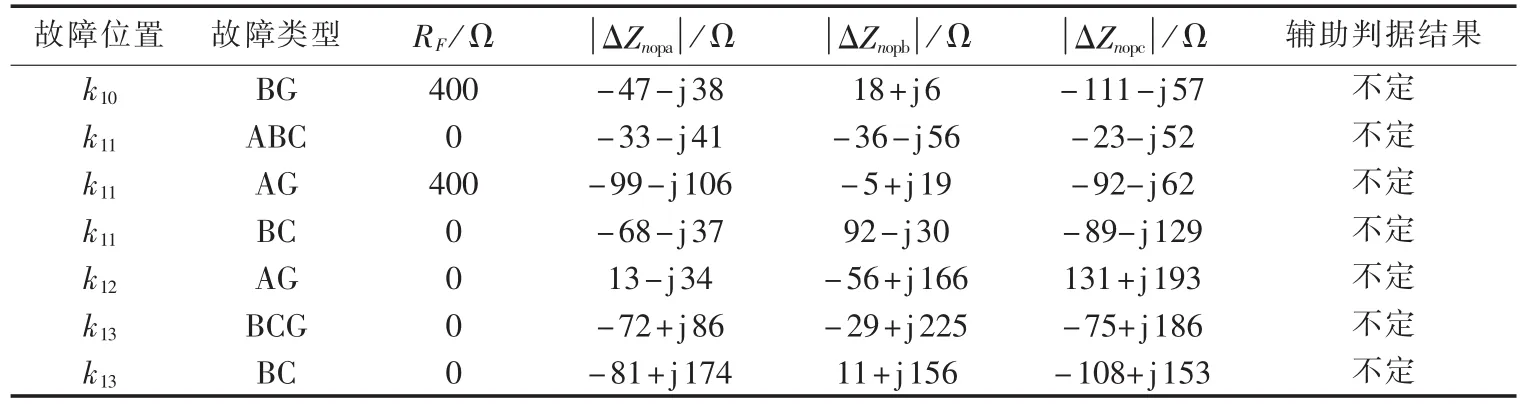
表4 n侧动模仿真的验证结果Tab.4 Verification results of dynamic emulation test at n side
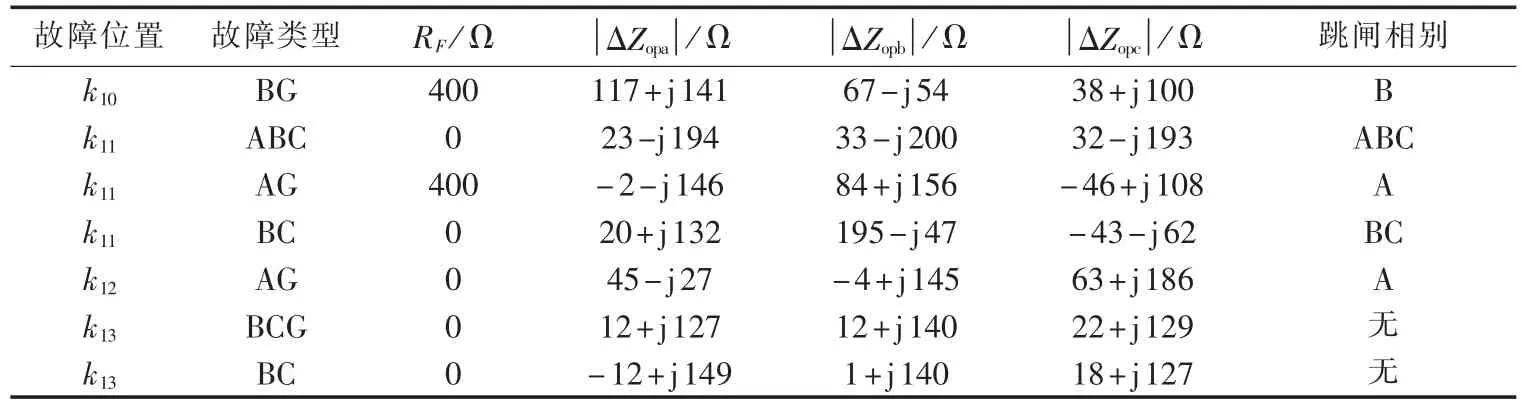
表5 纵向阻抗动模仿真的验证结果Tab.5 Verification results of dynamic emulation test for LI
c.当内部故障发生时,对于故障相,至少一端计算所得的测量阻抗明显小于式(21)所设限值,这个结果满足对系统阻抗识别的附加要求。
d.LI的结果基本没有受线路长度和额定电压等因素的影响。
e.文献[14]采用 500 kV、300 km EMTP 分布参数型的仿真模型,该阻抗幅值判据设置的动作范围为:

由于文献[14]没有记载设置式(22)(取自文献[14]的式(9)—(11))的理论依据,由此可以推测上述设置基本参照仿真数据的分布特点而人为设定,其数据分布范围相对分散。
f.本文所用动模模型的电压等级和线路长度均高于文献[14],因此受线路分布电容等因素的影响也明显大于文献[14]。判据式(21)阻抗幅值变化范围明显小于式(22),并且有充分的理论依据,其仿真结果也充分证实了上述理论分析的准确性。
g.本文与文献[14]最大的区别和改进之处在于增加了解耦算法并且考虑了系统与线路参数间的相互影响。由此可以认定本文所述方法使LI计算结果的稳定性较文献[14]有明显的提高。
7 结论
基于单相和三相线路模型,完成了对LI状态和性能的分析,由此充分证明对于外部故障,LI为被保护线路的正序阻抗,它能够确保相关纵联保护的安全和可靠性;对于内部故障,LI是外部等效系统阻抗负的相量和,它可以确保相关纵联保护的有效和灵敏度。LI的一个重要性能是有能力避免线路分布电容和数据不同步采样所带来的负面影响,它所具有的准确的解耦算法可满足实际需要,同时所配的辅助判据从原理上能够弥补LI所反映数值发散的问题,因此本文所提的纵联保护能够适用于各种运行环境。同样,动模仿真结果证明LI及相关纵联保护具有更高的可靠性和适应性。
