基于在线支持向量机的空对地攻击决策算法
2013-10-15何文龚
韩 伟,刘 敏,何文龚,陈 谋
(1.南京航空航天大学 自动化学院,南京 210016; 2.中国人民解放军 93413部队,山西 运城 044500;3.洛阳光电设备研究所 光电控制技术重点实验室,河南 洛阳 471009)
0 引 言
大量使用无人机对地攻击是现代战争的重要手段之一,是夺取现代战争的制信息权和制空权的关键。无人机在执行对地攻击任务过程中,面对复杂的战场环境,有大量信息必须不停地进行计算、判断、决策并做出相应的战术动作。其中决策是该过程中最重要的环节之一,对无人机能否顺利完成任务以及完成任务的效率具有非常重要的意义[1]。
地面目标包括坦克、装甲车、导弹发射车、军事指挥中心、机场、雷达站、桥梁和弹药库等,在战争中具有非常重要的地位,因此,利用无人机摧毁敌方地面目标具有非常重要的意义。无人机对地攻击决策是把所有要攻击的地面目标合理分配给无人机[2]。而影响决策过程的因素主要为目标威胁度[3],它是确定火力单元如何分配的重要依据之一。同时,威胁度的预测值及威胁排序也是进行对地攻击决策的依据。目前,无人机对地攻击决策是无人机领域的热点研究问题,文献[1]采用离散微粒群优化算法,很好地解决了多无人机多目标的任务分配问题,但模型中没有考虑目标威胁度这个重要指标。文献[3]利用改进层次分析法,解决了多目标决策优选问题,但由于不同人的主观标度相差较大,使最终的评估结果带有一定的主观性。
为充分利用目标威胁度这个重要指标,并克服人参与威胁度评估带来的主观性,笔者采用在线支持向量机算法对目标威胁度进行预测,并根据预测出的地面目标威胁度排序进行攻击决策。支持向量机最初广泛应用于模式识别及函数回归等传统机器学习领域。最近有文献用支持向量机解决动态系统的辨识、在线建模等问题,都得到了很好的效果[4,5]。为了实现在线建模、提高模型精度,把在线支持向量机算法引入到攻击决策过程中,以提高攻击决策的时实性和准确性,对攻击决策的研究具有重要意义。
针对无人机对地攻击决策的问题特点,充分考虑战场形势的复杂性、多变性,以及作战时机的重要性,如何在有限的时间内实现对战略价值高、对我方威胁度大的目标进行有效攻击,对提高我方生存能力和打击敌方重要目标显得尤为重要。但鉴于地面目标防御与机动能力越来越强,如何综合考虑复杂多变的战场形势,实现对目标威胁度的实时计算,以辅助火控系统进行快速攻击决策,具有重要的军事价值。在线支持向量机具有很好的动态建模能力和学习能力,能实时计算地面目标的威胁度,并根据威胁度及无人机对目标攻击的优先权进行攻击决策。该方法具有可在线训练、建模速度快、泛化能力强等优点,能较准确地计算出目标威胁度指标,为攻击决策提供可靠的依据,为无人机自动实现对地目标的有效打击奠定了基础。
1 目标威胁度模型的建立
对多个地面目标进行攻击决策的问题,可转化为对地面目标威胁程度进行评估及排序的过程,笔者主要考虑地面目标的射击效率[6-8],选取的地面目标威胁度指标有:火力单元数n、可靠度Pr、生存能力Ps、搜索能力Pf、毁伤能力Pd和抗干扰能力Pk。
1.1 指标说明
1)火力单元数n是指地面目标能独立地完成搜索、跟踪、瞄准和射击的综合系统个数。
2)可靠性Pr是指在给定条件下,系统完成特定功能的概率。
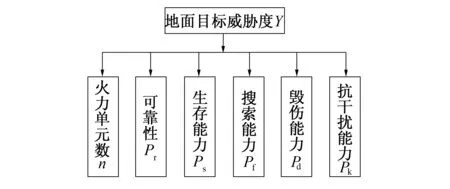
图1 地面目标威胁度指标体系
3)生存能力Ps是指系统在任务环境下,受到对方的各种手段攻击后还能维持其他各项性能的概率。
4)搜索能力包括目标识别能力和目标捕捉能力,这里用发现目标概率Pf表示。
5)毁伤能力是武器系统最根本的效能量度,通常用对目标的毁伤概率Pd表示。
6)抗干扰能力Pk是系统在受到对方电子等各种干扰的情况下,能保持其正常功能的概率。
无人机对地面目标攻击决策的指标体系如图1所示。
1.2 目标威胁度计算
为了生成训练所需的目标威胁度样本数据,需要对根据以上建立的地面目标威胁度指标体系,对地面目标威胁度进行计算。笔者选择层次分析法[9],具体步骤如下。
1)构造两两比较判断矩阵
A=(aij)n×n
(1)
其中n为评估体系的指标个数,aij为第i个指标对第j个指标的重要程度,1表示两个指标相比,具有同等的重要性,3表示两个指标相比,前者比后者稍重要,以此类推,9表示两个指标相比,前者比后者极端重要,2、4、6、8表示上述相邻判断的中间值。如果前者比后者重要性之比为aij,则后者比前者的重要性之比为aji=1/aij。
2)将判断矩阵A按列归一化,按行求和,再对列归一化,得权重向量
w=((wi)1×n)T
(2)
3)判断矩阵A的最大特征值
(3)
对应的特征向量W=((μi)1×n)T就是评估指标的权重向量。由于评估系统的复杂性以及主体认识的局限性,应对判断矩阵的一致性进行检验[9]。
4)采用幂指数法计算目标威胁度指标
(4)
通过以上步骤,可得到地面目标威胁度的数据样本,为利用在线支持向量机建立目标威胁度在线训练模型,并进行无人机对地攻击决策做准备。
2 基于在线支持向量机的对地攻击决策技术
支持向量机最初广泛应用于模式识别及函数回归等传统机器学习领域,取得很好的效果。现在将在线支持向量机算法引入到攻击决策过程中,使用在线支持向量机进行动态建模,能提高系统模型精度,增强系统实时性,对攻击决策问题的研究具有重要意义。
2.1 在线支持向量机的原理及实现
把支持向量机估计指示函数中得到的结论推广到实函数中,即支持向量机回归[9,10]。根据统计学习理论,构造线性回归方程[11]
f(x)=wΦ(x)+b
(5)
其中非线性映射Φ把数据x映射到高维特征空间F,w为在空间F中的特征向量,b为偏置值。

(6)
约束条件为
(7)
其中ε为不敏感损失函数,C为惩罚系数。
引入拉格朗日函数和对偶变量[11]
(9)
(10)
于是可得
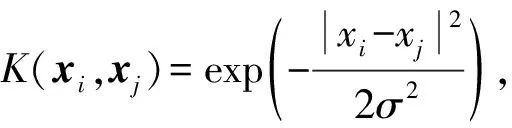
(12)
1)错误支持向量集合E:E={i||θi|=C,|h(xi)|>ε};
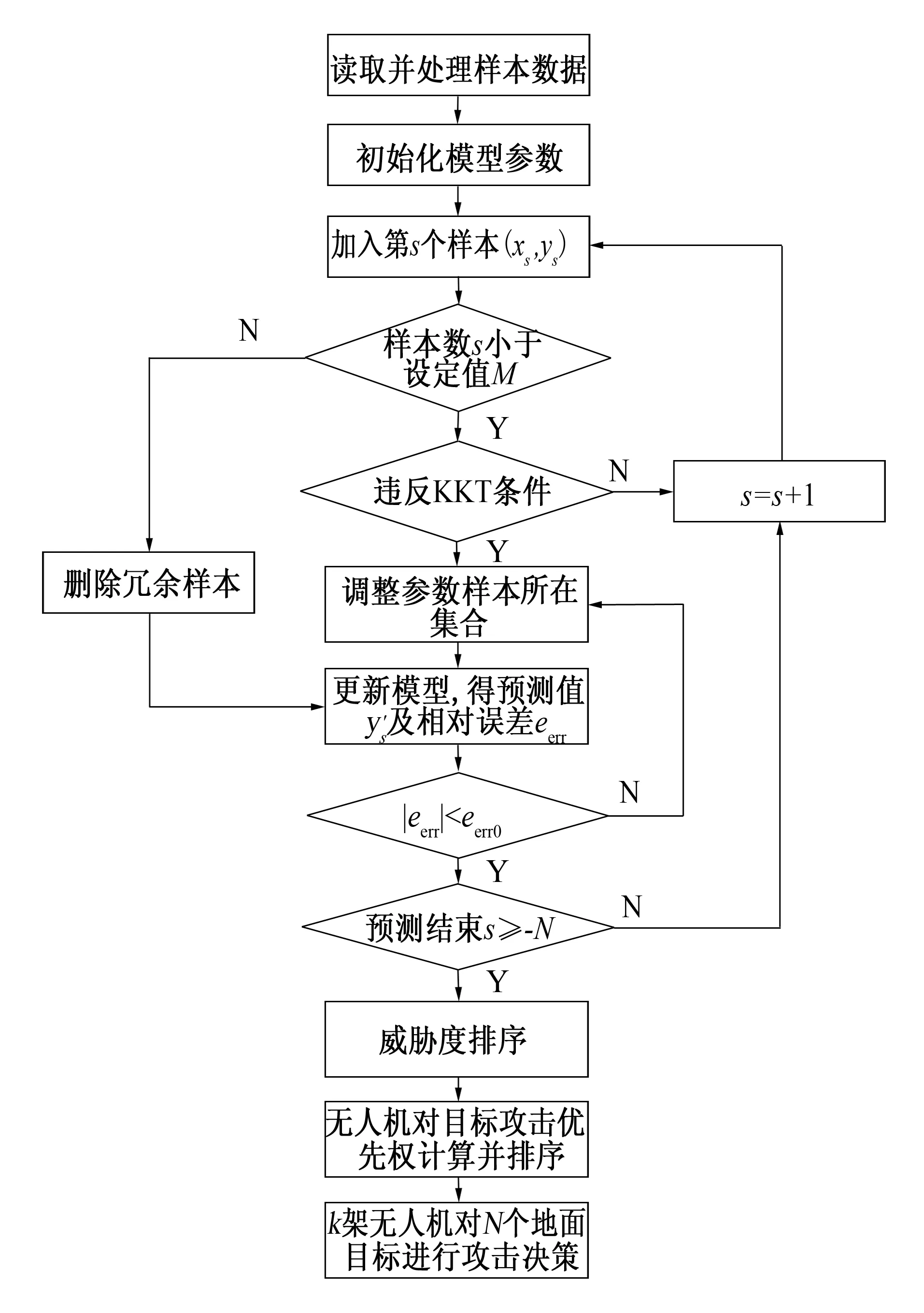
2)边界支持向量集合S:S={i|0<|θi| 3)剩余样本集合R:R={i||θi|=0,|h(xi)|<ε}。 上述3个集合的分布特征如图2所示。 图2 集合S、E、R的分布特征 在线支持向量机算法的实现包括增量算法[13,14]和减量算法[15]两部分。增量算法:将新样本(xs,ys)加入训练集中,并逐步调整θs及偏置值b,直到新样本进入集合S、E、R中的一个。减量算法:算法逐步调整θs及偏置值b,使要去除的样本θs变为0,也使样本(xs,ys)移入保留样本集合R,目的是将一个样本从训练集合中去除,而使剩余样本仍满足KKT条件。算法的具体实现参见文献[16]。由以上3个集合的定义可知,当有新样本加入时,S和E的边界是可变的。即在训练过程中,因为新样本xs的影响,会逐步改变系数偏差θs和样本xs的边界函数h(xs),原有的一些样本归属的集合也会发生改变。 在线支持向量机具有可在线训练、建模速度快和泛化能力强等优点,能满足无人机对地攻击决策的实时性要求。因此,可把在线支持向量机方法引入到无人机对地攻击决策算法中,具体步骤如下。 2.2.1 数据样本选取 样本的选取对目标威胁度评估很重要,只有合理选择样本才能得出科学的评估模型。选取的样本D={(Xi,Yi)|i=1,2,…,N},包括样本的规模N和样本的指标值(Xi,Yi)(Xi代表第i个地面目标威胁度的6个指标值n、Pr、Ps、Pf、Pd、Pk),样本的规模N具体指地面目标的个数,样本指标值(Xi,Yi)反映地面目标系统本身的性能。 2.2.2 数据样本处理 根据数据样本的有限性,一般把样本分成两部分:一部分用于训练,剩余部分用于测试。采用数据滑动窗方式[13](见表1),构造M个不同的训练样本及(N-M)个不同的测试样本,充分利用给定的样本数据分别对目标威胁度的计算结果进行测试,以检验结果的合理性和科学性。 为了便于分析,对目标威胁度指标进行归一化处理,归一化方法如下 (13) 其中N为总样本数,y1为威胁度指标y归一化后的威胁度指标。 表1 目标威胁度数据样本构造 2.2.3 攻击决策过程 图3 基于在线支持向量机的对地攻击决策算法流程图 设有k架(编号为1,2,…,k)无人机,对N个地面目标进行攻击,则基于在线支持向量机的对地攻击决策算法如下: 1)构建训练样本集{(xi,yi)|i=1,2,…,M},M为训练样本数; 2)加入第s个样本(xs,ys),如果训练样本的数量小于设定值M,则转到3); 否则,转到4); 3)利用在线支持向量机增量算法调整参数和样本所在集合,更新地面目标威胁度模型,转到5); 4)利用减量算法删除冗余的样本,转到5); 7)如果样本个数s≥N,则转到8); 否则,s=s+1,转到2); 9)利用文献[17]中提到的信息熵算法计算空地多目标攻击优先权,求出无人机对地面目标攻击的优先权矩阵,然后按照威胁度高的目标优先被攻击、用对该目标优先权高的无人机优先进行攻击的原则对地面目标进行攻击决策。 基于在线支持向量机的攻击决策算法流程如图3所示。 该实例为4架无人机(A、B、C、D)对20个地面目标进行攻击,目标的各项性能指标如表2所示。计算机的主要配置情况为:32位Win7专业版操作系统,2.1 GHz双核处理器,4 GByte内存(实际可用2.96 GByte),仿真平台为VS 2008。攻击决策过程仿真如下。 根据实际情况并考虑目标的差异,确定地面目标的各项性能指标,构造判断矩阵 计算权重向量 W=(μ1,μ2,μ3,μ4,μ5,μ6)T=(0.040 9,0.138 6,0.226 6,0.158 2,0.347 1,0.088 6)T 通过式(4)计算目标威胁度指标 利用以上建立的目标威胁度模型,生成20组数据样本,并对目标威胁度指标进行归一化处理,得到的训练样本如表2所示。 表2 训练样本 选取其中的16组数据样本进行训练,剩余4组数据样本用来测试,采用数据滑动窗方式,构造不同的训练样本及测试样本(见表3)。 对以上选取的样本,利用在线支持向量机对地面目标威胁度建模,由模型求出目标威胁度并排序,根据威胁度大的目标先被攻击的原则进行攻击决策。 表3 目标威胁度数据样本构造方法 分别选择RBF核函数和多项式核函数对数据样本进行训练。通过仿真发现,这两种核函数对样本训练精度影响差别不大,而利用RBF核函数的训练时间(62 ms)要明显小于多项式核函数的训练时间(83 ms),因此,笔者选取高斯RBF函数为核函数。于是,可初始化参数:C=3,ε=0.001,核函数类型:RBF,核函数宽度:σ=10。 输入样本数据:从文本文件samples.txt读入,分别按数据滑动窗方式选择16组参数为输入样本,剩余4组为测试输出。 训练结果:随机选取一组输入样本进行训练并对剩下的样本进行测试,为比较该算法的性能,这里引入相对误差eerr,对预测效果进行比较分析 (14) 其中y为计算得到的目标威胁度,y′为用训练模型计算出的目标威胁度。 如取x2,x3,…,x17进行训练,观察x18,x19,x20,x1对应的输出和实际输出的对比,结果如表4所示。 表4 计算结果及误差分析 在地面坐标系中,无人机坐标为:A(200,0,-6 000),B(0,200,-6 000),C(0,-200,-6 000),D(-200,400,-6 000),20个地面目标坐标分别为1(4 380,270,0),2(4 200,300,0),3(5 080,280,0),4(4 000,150,0),5(5 220,240,0),6(4 350,480,0),7(4 750,170,0),8(4 280,210,0),9(4 490,220,0),10(4 150,390,0),11(4 880,210,0),12(5 290,220,0),13(4 280,230,0),14(4 640,400,0),15(4 520,340,0),16(4 590,150,0),17(4 870,250,0),18(4 630,0,0),19(5 350,30,0),20(4 790,10,0)。按照目标的重要程度对目标打分(0~10分):8,7.5,10,7.6,8.2,9.3,5,3,8.4,8.9,9.6,9.5,9.8,6.4,7.3,8.4,9,5.5,8.6,8.8。把无人机携带武器和地面目标的武器性能进行对比,求出武器性能优先权:0.93,0.88,0.45,0.3,0.7,0.6,0.8,0.5,0.9,0.78,0.7,0.65,0.78,0.89,0.95,0.5,0.8,0.74,0.82,0.7。再根据无人机和目标的坐标可以求出无人机和目标间距离、目标方位角和目标俯仰角,进而求出目标的方位优先权和俯仰优先权。最后利用信息熵算法(具体过程参考文献[17]),构造决策矩阵、归一化处理、计算信息熵和计算熵属性权重,得到4架无人机对20个地面目标的攻击优先权矩阵 因此,可根据目标威胁度及攻击优先权矩阵,按照威胁度高的目标优先被攻击、对该目标优先权高的无人机优先进行攻击的原则,对地面目标进行攻击决策。根据威胁度指标顺序,首先攻击威胁度最高的目标6,对6具有最高优先权的无人机为D,故D→6(表示无人机D攻击编号为6的地面目标,下同),同理B→11、D→16、B→5、A→20、C→9、B→2、B→12、D→7、A→8、A→19、A→13、D→1、B→14、C→10、A→4、D→17、C→3、A→18、B→15。考虑到该攻击顺序中存在一架无人机依次连续攻击多个相邻优先权顺序目标的情况,将会影响无人机编队的整体攻击效率。为使任务分配更合理,可以把优先权相同的目标尽量分配给未连续攻击相邻优先权顺序目标的无人机,必要时可在同一目标优先权相差不大的无人机中适当调整任务安排。攻击顺序安排如表5所示。 表5 攻击顺序安排 从表5可看出,调整后的攻击决策顺序为:D→6,B→11,D→16,B→5,A→20,C→9,B→2,C→12,A→7,C→8,D→19,A→13,D→1,B→14,C→10,A→4,D→17,C→3,A→18,B→15。其中表5最右边4列数据为无人机攻击地面目标的安排情况,未带圈的数字为调整后对应无人机攻击的地面目标的编号,带圈的数字为备选的攻击目标编号。 通过以上的实例仿真,证明了在线支持向量机算法具有很好的精确度、稳定性及泛化能力; 同时训练样本平均时间为62 ms,说明该算法的速度很快。所以该方法完全可以满足在线训练建模及决策,能适应无人机对地目标攻击决策的实时性要求。该方法在核函数宽度σ很小时,模型的拟合效果非常好,但泛化能力非常低; 相反,当σ偏离一定范围时,模型很难满足相应的精度要求。因此,需要在模型精度和泛化能力之间进行折中考虑,下一步也可以通过优化算法实现。 笔者应用在线支持向量机研究了无人机对地目标攻击决策算法,充分利用在线支持向量机的动态建模能力,实现对地面目标威胁度的计算,并根据目标威胁度和无人机攻击优先权进行攻击决策。所研究的算法能很好地解决传统的对地面目标攻击决策算法的人为主观性、不能在线建模、模型精度不高、泛化能力不强的问题。因而,基于在线支持向量机的无人机对地目标攻击决策算法能较准确地计算出目标威胁度指标,为无人机对地面目标攻击决策提供可靠依据。 参考文献: [1]宋磊,黄长强,吴文超,等.多UCAV协同目标攻击决策[J].系统工程与电子技术,2011,33(7):1548-1552. SONG Lei,HUANG Chang-qiang,WU Wen-chao,et al.Target Attack Decision-Making for Cooperating Multi-UCAV[J].Systems Engineering and Electronics,2011,33(7):1548-1552. [2]邓有训,余志惠.电子对抗力量实施协同作战问题之探讨[J].空军雷达学院学报,2010,24(2):129-133. DENG You-xun,YU Zhi-hui.Discussion about Employing ECM Force to Implement Coordinated Operation[J].Journal of Air Force Radar Academy,2010,24(2):129-133. [3]杨州,袁卫卫,王明利.基于改进层次分析法的对地攻击方案优选决策[J].火力与指挥控制,2011,36(1):111-113. YANG Zhou,YUAN Wei-wei,WANG Ming-li.Research on Optimum Decision-Making of Air-to-Land Attacking Schemes Based on Improved AHP[J].Fire Control &Command Control,2011,36(1):111-113. [4]王定成,方廷健.一种基于支持向量机的内模控制方法[J].控制理论与应用,2004,21(1):85-88. WANG Ding-cheng,FANG Ting-jian.Internal Model Control Approach Based on Support Vector Machines[J].Control Theory &Applications,2004,21(1):85-88. [5]何峻峰,张曾科.基于支持向量机的逆系统离散控制方法[J].清华大学学报,2005,45(1):100-106. HE Jun-feng,ZHANG Zeng-ke.Support Vector Machine Inverse Control of Nonlinear Discrete Systems[J].Journal of Tsinghua University:Science &Technology,2005,45(1):100-106. [6]李京,杨根源.基于神经网络的地面目标威胁度分析[J].兵工自动化,2012,31(3):15-18. LI Jing,YANG Gen-yuan.Analysis of Ground Targets Threatening Level Based on Neural Network[J].Ordnance Industry Automation,2012,31(3):15-18. [7]孙巨为,贾春雨.陆军进攻战役防空效率指标及制空权评估[J].火力指挥与控制,2008,33(4):138-142. SUN Ju-wei,JIA Chun-yu.Research on Air-Defence Efficiency Indexes and Air Domination Evaluation in Offensive Combat of the Army[J].Fire Control and Command Control,2008,33(4):138-142. [8]符永军,方棉佳,张永顺.模糊多因素多层次评判在目标威胁度中的应用[J].火力与指挥控制,2004,29(3):88-90. FU Yong-jun,FANG Mian-jia,ZHANG Yong-shun.The Application of Fuzzy Multi-Factor and Multi-Hierarchy Synthetic Judge to Evaluation of the Air Targets’ Threat[J].Fire Control &Command Control,2004,29(3):88-90. [9]孔繁森,王军,孙海港.基于层次分析法的发动机缸体生产线设备可用性的模糊综合评价[J].吉林大学学报:工学版,2008,38(6):1333-1335. KONG Fan-sen,WANG Jun,SUN Hai-gang.Fuzzy Comprehensive Evaluation of Equipment Usability of Engine Cylinder Block Production Line Based on AHP[J].Journal of Jilin University:Engineering and Technology Edition,2008,38(6):1333-1335. [10]VAPNIK V.The Nature of Statistical Learning Theory[M].New York:Springer,1999. [11]王定成.支持向量机建模预测与控制[M].北京:气象出版社,2009:20-27. WANG Ding-cheng.Support Vector Machine Modeling Prediction and Control[M].Beijing:China Meteorological Press,2009:20-27. [12]郑小霞,钱峰.基于支持向量机的在线建模方法及应用[J].信息与控制,2005,34(5):636-640. ZHENG Xiao-xia,QIAN Feng.ASVM-Based Online Modeling Method and Its Application[J].Information and Control,2005,34(5):636-640. [13]李雪梅,丁力行,陈嘉澍.在线支持向量机在数控铣床刀具磨损预测建模中的应用[J].现代制造工程,2011(7):98-101. LI Xue-mei,DING Li-xing,CHEN Jia-shu.The Application of Online Support Vector Machine to Tool Wear Prediction Modeling of Digital Control Milling Machine[J].Modern Manufacturing Engineering,2011(7):98-101. [14]陈进东,潘丰.基于在线支持向量机的非线性内模控制[J].计算工程与应用,2009,45(9):18-20. CHEN Jin-dong,PAN Feng.Nonlinear Internal Model Control Based on Online Support Vector Machine[J].Computer and Applications,2009,45(9):18-20. [15]李永丽,刘衍珩,肖见涛,等.基于支持向量机的增量学习算法[J].吉林大学学报:理学版,2010,48(3):464-467. LI Yong-li,LIU Yan-heng,XIAO Jian-tao,et al.Incremental Learning Algorithm Based on Support Vector Machine[J].Journal of Jilin University:Science Edition,2010,48(3):464-467. [16]MA JUNSHUI,THEILER J,PERKINS S.Accurate on-Line Support Vector Regression[J].Neural Computation,2003,15(11):2683-2701. [17]陈中起,周中良,于雷,等.基于改进信息熵的空地多目标攻击优先权决策[J].系统工程与电子技术,2011,33(2):29-32. CHEN Zhong-qi,ZHOU Zhong-liang,YU Lei,et al.Priority Decision of Air-to-Surface Multi-Target Attack Based on Improved Entropy[J].System Engineering and Electronics,2011,33(2):29-32.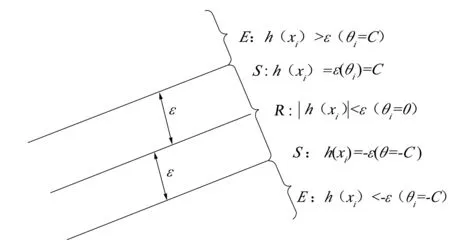
2.2 基于在线支持向量机的对地攻击决策算法

3 仿真实例
3.1 样本的选择与处理

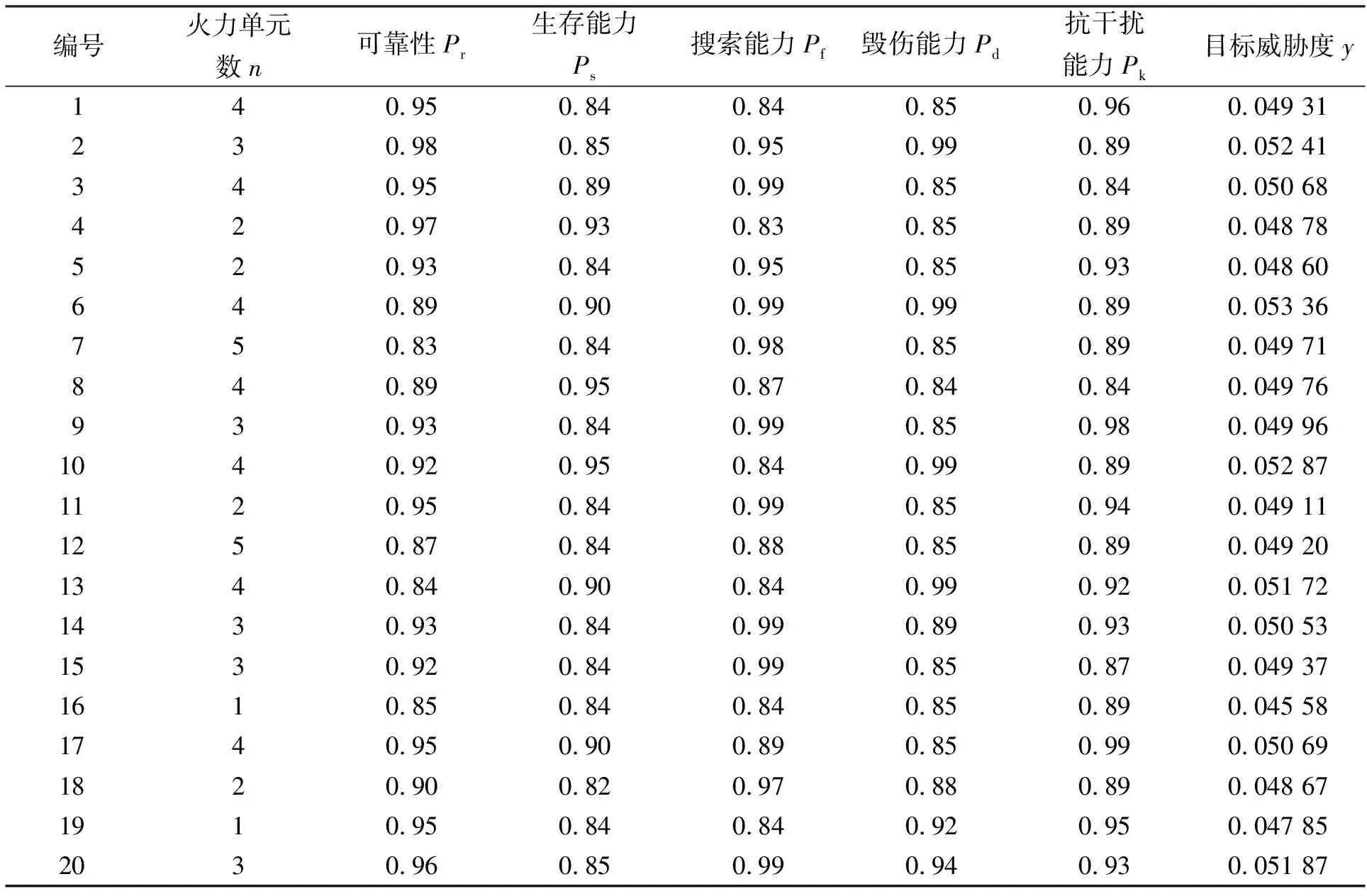
3.2 仿真过程



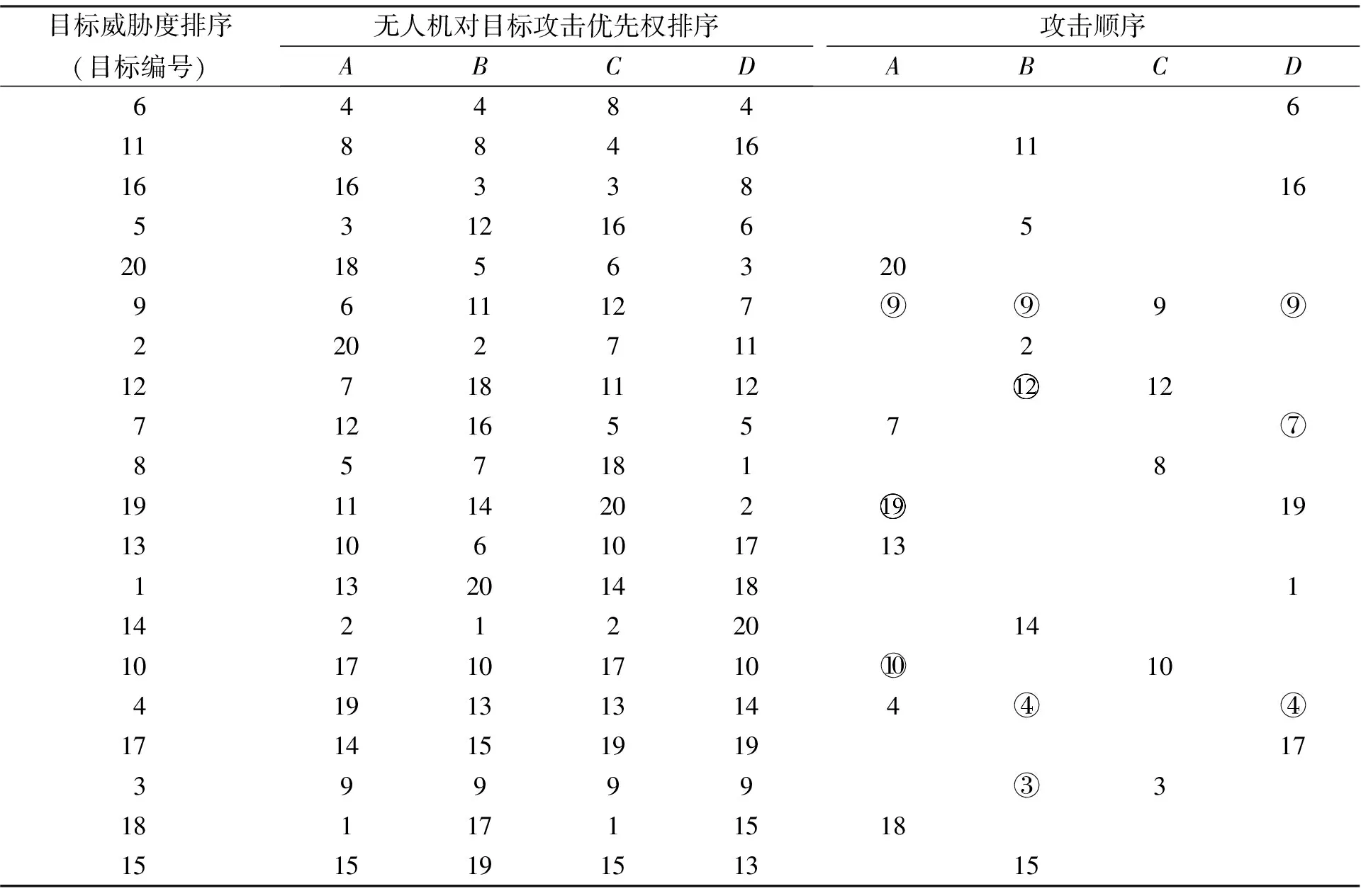
4 结 语
