基于超立方路径规划的发动机再制造物流作业调度策略
2013-10-15田大庆李炎炎
高 健,龙 伟,田大庆,李炎炎
(四川大学 制造科学与工程学院,成都 610065)
0 引言
航空发动机再制造不同于传统的航空发动机生产制造,其具有多品种,小批量等特点,尤其对于发动机主件和附件的再制造,其工艺工序的多样性程度和复杂程度十分突出,这与传统的刚性离散制造系统依据输入/输出来作决策有着本质的区别。当我们把众多型号发动机的传统生产方式转化为规模化可重构的制造模式时,这就要求其生产组织形态必须适应经常变化的作业过程。目前,面向系统的可重构研究主要集中在以机器为模块进行制造系统的重构[1]。
自动导航车(Automated Guided Vehicles,AGV)是一种自动化的无人驾驶的智能化搬运设备,属于移动式机器人系统,能够沿预先设定的路径行驶,是现代计算机集成制造系统中的关键设备之一[2]。可重构制造系统就是利用AGV的循迹特点进行生产组织形态的重组,从而使得航空发动机再制造车间能够适应经常变化的加工流程。目前这方面研究集中在AGV本身技术以及AGV作业规划调度方面。
对于复杂再制造系统,其车间作业调度路径的拓扑结构可以有多种选择,其算法主要解决的是AGV小车从起点到目标点的路径问题[3],主要有状态空间法[4]、神经网络法[5]、栅格法[6,7]、免疫网络算法[8]、粒子群算法[9]和遗传算法[10]等。
但是,现有的拓扑规划理论和调度策略普遍存在着难以解决多目标,多约束,很少涉及实时调度,依赖输入/输出进行决策等问题:因此,研究探索能够快速响应生产形态变化和过程决策传导的作业规划调度理论是航空发动机再制造系统实现可重构的重点和难点。
1 基于超立方路径规划的新方法
1.1 超立方的概念
本文提出的超立方路径规划思想,源于数学物理上的“超立方体”概念[11],超立方体描述方法是寻找一个聚类的最小外接立方体,使其包含数据集中所有的数据点[12]。我们从超立方体中抽取一个胞粒作为基本立方体,如图1(a)所示,由于它的八个角点可以通过多条路径相连,于是可将每个角点都规为一个加工工位、仓储货架等。当需要并行协同加工工位或仓储货架之间的作业流程时,我们可按一定的规则来定义连接在立方体上的角点。
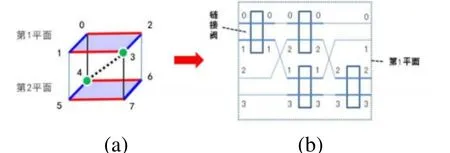
图1 在物流作业路径中引入超立方概念
设两个相邻角点的连接为一个链接语句,并以“面”为基本单元,如图1(a)中 0-1-2-3 的上平面和 4-5-6-7 的下平面。如果把一个链接语句,定义成两个角点连接的“链接阀”,则一个基面四个角点的两两互连,可用图1(b)的链接展开图来表示。同时,第一平面的每一个角点都可以与第二平面的任一角点相连且每一种链接方式都有唯一展开图与之对应。如用图1(a)所示的角点3和角点 4 之间的连线,将立方体上下两基面连接起来,我们便可得到一种如图2所示的立方体角点链接展开图。

图2 单胞粒上下基面角点的连接路径
1.2 链接算法的简单介绍
现规定:
设定一 设链接语句函数式为 link(x,y),x为起始角点值,y为终止角点值,它们的三位二进制表达式为:

设定二 设 Box(i,j)为超立方角点链接阀,它的状态对应于链接语句link(x,y)的“位”状态值,并定义:
当 Box(i,j)=0 时,则表示i与i直链,或j与j直链;
当 Box(i,j)=1时,则表示i与j交链,或j与i交链;
于是,link(x,y) 的位状态可表示为:

例如,当角点 0与角点1的链接,其 link(0,1)=[10],则有:

可见,Box(0,1)=1,表示角点0与角点1交链;Box(0,1)=0,表示角点0与角点1直链。
设定三 设链接语句的运算规则为二进制的“位加”运算,即两个二进制同位相加后取其个位的值,并用运算符“”来表示。根据定义,我们对图2中上虚框所表示的第一基面角点的链接算法推导如下:
1)相同角点的直链语句:
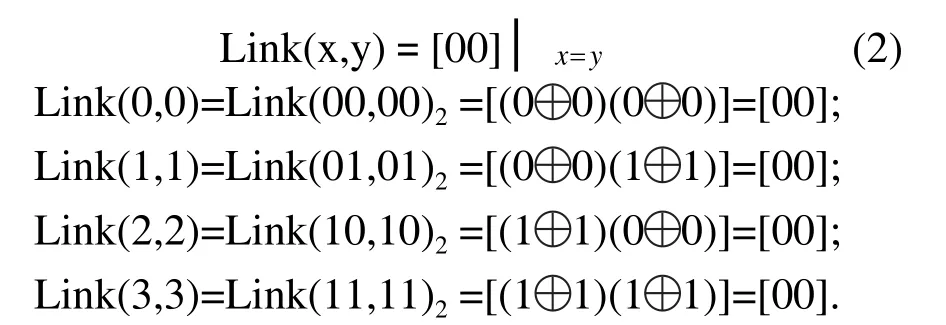
2)不同角点的直链语句:

例如:

3)间隔角点的链接语句:
由于不同角点的直链语句具有可逆性,因而可以用它来生成间隔角点的链接状态,即把相邻角点的首尾状态值连接后消去,可用“⊙”表示。通常,间隔角点的链接具有多条路径可以选择,如:

4)交叉角点的链接语句:

对于图2中下虚框所表示的第二基面角点的链接算法,只需将角点值减去(k-1)×4 后(k 为立方体的基面数),套用上平面的链接算法,然后将上下两个基面的链接值带入交叉链接语句即可。其他基面也照此类推。
1.3 引入估价函数
由上述算法介绍得知,两角点之间时常存在多条链接路径,因此存在路径最优问题,选择的依据通常有时间因素,距离因素,拥堵因素以及直角拐点因素等[13],为方便起见,本文只引入距离估价函数以取得最优解。引入笛卡尔坐标系,保存每个角点的坐标值。估价函数形式:

上述算法,我们把它定义为“基于超立方模型的路径链接算法”。
2 调度流程
如图3所示,根据车间实际情况设置节点布置位置,并提取节点笛卡尔坐标值,设置不连通路径,当AGV小车接受任务时应先根据任务的起始和终止点求出两节点分别所在基面,以便得出链接路径中共有多少交叉角点链接。

图3 调度流程
根据调度算法求出的路径不一定都符合车间的实际情况,此时就需要剔除原先设定的不连通路径。每一条符合要求的路径均由若干节点组成,每依次相邻节点间均有一估价函数值,而这条路径的估价函数值是所有节点函数值的总和,最优路径就是依据最小估价函数值来选择。
3 调度算法模型与物理形态的转换
我们可进一步将图2所示的链接规则,转换为相应的制造物流作业路径连接的物理形态,为方便可行,我们将工位 2 与工位 3 的位置互换,将工位 6 与工位 7 的位置互换,图 4就是采用交链语句来连接上下两个基面的多工位路径链接的物理形态示意图。
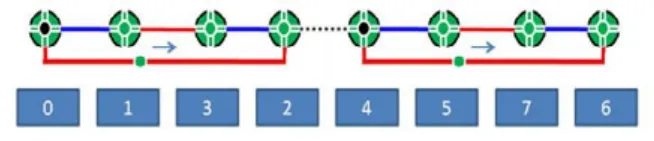
图4 超立方路径的物理结构
对于多基面问题,我们只需要在图4的基础上加以顺延即可,如图5所示。

图5 多重超立方路径的物理结构
在此基础上,根据航空发动机再制造车间特点,本文给出了车间布局的示意图,如图6所示。

图6 航空发动机再制造车间布局示意图
4 算例
例如某一航空发动机再制造车间布局如图7所示。其中0-3节点为航空发动机主体再制造单元,4-11节点为物料配送中心入仓口,12-18节点为航空发动机控制器再制造区,现物流小车调度任务为从货架3上取一零件送至工位11处。
具体处理方法如下:
1)提取每个角点坐标信息,如表1所示,根据车间实际摆放情况,设定第一基面和第二基面之间只有0和4以及2和6可通,在同一基面内各节点都可通;

表1 各角点笛卡尔坐标
2)对于起始角点3,求的K=1,即在第一基面,终止角点4,求的K=2,即在第二基面;
3)起始角点和终止角点不在同一基面,且其中含有一个交叉角点链接;
4)剔除步骤1中设定的不连通路径,根据超立方理论模型,共得出6种链接路径,如表2所示;
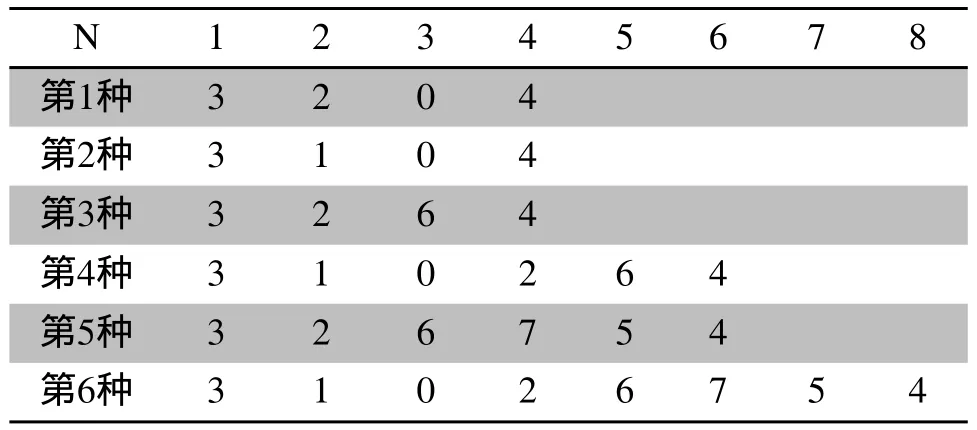
表2 枚举链接路径
5)利用估价函数,求的每种路径的函数值如表3所示;
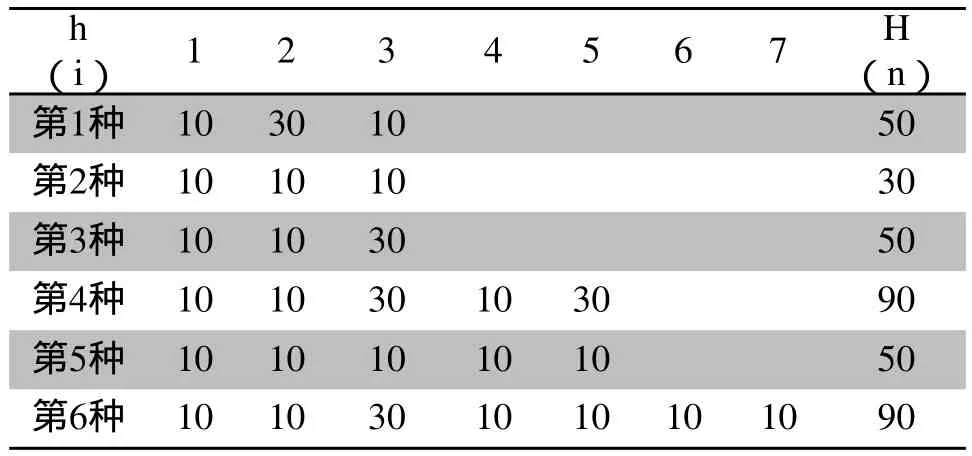
表3 估计函数值
6)由表3得最优路径为第2种,其二进制表述为:
其中:
link(3,4)=link[link(3,0) (1)]
link(3,0)=link(3,1)⊙link(1,0)=[0101]
所以link(3,4)=[01011]。
5 结论
尽管人们在互联网络、神经网络、集成电路、通信技术等领域,对超立方体拓扑结构及路径理论进行了大量研究,但本质上大都侧重在超立方体的全域“聚类点基元”的大规模并行处理的理论技术局面,需要进行复杂的数学运算处理。本文研究,通过“面基元”来构造与可重构制造物流模态相对应的“网格结构”,并提出了“超立方路径的链接算法”,为航空发动机再制造车间的作业过程提供了实时调度,传导敏化的新方法,本算法避免了全域搜索所带来的计算量大的问题,利用人为设置路径通断,既进一步增强了系统的可重构性也强调了过程决策,但是更加普适,通用的超立方理论及其传导模态还需要进一步研究。
[1] 王晓勇,臧铁钢,陈富林.制造系统可重构控制技术研究[J].制造业自动化,2007,11(29):23-27.
[2] 徐清.自动导引小车系统的设计与实现[D].苏州:苏州大学,2006.
[3] 孙奇.AGV系统路径规划技术研究[D].浙江,浙江大学,2012.
[4] 胡正兴,李一民,詹跃东.自动导引小车局部智能避障的A*算法[J].昆明理工大学学报,2005,30(5):51.
[5] 肖本贤,齐东流,刘海霞,等.动态环境中基于模糊神经网络的AGV路径规划[J].系统仿真学报,2006,18(9):2401.
[6] 邓高峰,张雪萍,刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群算法[J].控制理论与应用,2009,26(s),879-883.
[7] 李天成,孙树栋,高扬.基于扇形栅格地图的移动机器人全局路径规划[J].机器人,2010,32(4),547-552.
[8] 方庆馆,黄建中.基于环境地图的AGV路径规划免疫网络算法研究[J].起重运输机械,2010,20(3):42-4.
[9] 边培莹,李德信,包宝军,路燕.粒子群算法在生产物流调度中的应用研[J].计算机工程与应用,2010,46(17):220-223.
[10] ZHAN Y u-dong,LUO Y ing.The goods-f low ing system AGV technology of Yuxi cigarette factory and the developmental research of AGV nationalization technology[C]∥IEEE International Vehicle Electronics Conference. Piscataway:IEEE Press,1999:425-428.
[11] 林崔琴,超立方图和超立方有向图的同构因子分解[J].清华大学学报(自然科学版),1992,32(3):24-29.
[12] 刘英帆,崔江涛.基于联合聚类的超立方体高维索引[J].计算机科学与探索,2012,06(00).
[13] 贺丽娜.AGV 系统运行路径优化技术研究[D].南京,南京航空航天大学,2012.
