液体火箭发动机泵动态特性水力试验研究

杜大华，黄金平，邢理想，徐浩海

（西安航天动力研究所，陕西西安710100）

0 引言

泵是对火箭动态特性影响最大的组件之一，进行泵动特性水试在火箭POGO振动、推进系统动力学研究中是一项不可缺少的基础性工作。美、日、俄、乌、法等国在泵动特性研究领域做了大量的理论研究和试验工作[1-5]，主要研究者有C.E.Brennen， S.Rubin， T.Shimura， A.J.Acosta，K.Kamijo和M.Iacopozzi等。虽然国内外对泵动特性无论在理论上或试验上都进行了大量的研究，但由于泵结构和流路十分复杂，影响泵动特性参数的因素较多，必须采用试验分析与理论计算相结合的方法来获取上述参数。我国新一代大型运载火箭研制也面临POGO设计技术问题，研究新型号泵动态特性是必须进行的工作。

对于泵动特性试验，一般是进行泵动态水试，在有条件的前提下可进行真实介质冷流试验和动特性热试车。然而，冷流试验和发动机动特性热试车试验规模太大，人工激励对试验的影响无法准确评估，风险过大，因此根据工程研制的需要及试验条件的限制，决定先进行泵动态水试。用水代替真实介质试验可以多次重复进行，采用水试将基本问题搞清楚后，再进行价格昂贵的真实介质试验对结果进行修正。

在对泵常规水力试验台进行适当改造的基础上，以常温水为试验介质，开展了全尺寸降转速的某型涡轮氧泵动态特性水力试验。

1 试验原理

依据泵的动态方程和连续方程，忽略泵入口和出口管轴向振动和转速波动的影响，得到气蚀泵的流体动力学传递方程

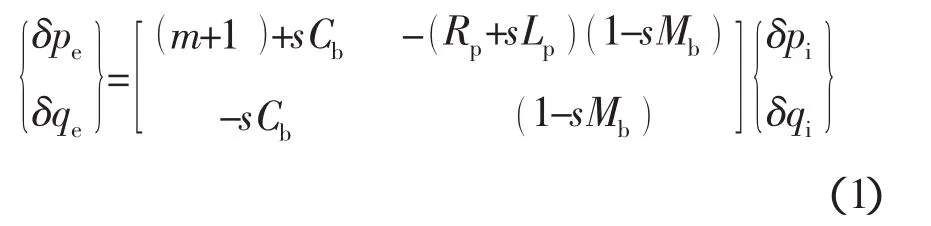
式中：δpe，δqe和 δpi，δqi分别为泵入口和出口的脉动压力和脉动质量流量；Rp，Lp，Cb，Mb和（m+1）分别为泵阻力、惯性、气蚀柔度、质量流量增益因子和动增益。这样，可将对泵液路动力学研究转化为对泵关键动态参数的识别问题。

1.1 泵阻力

阻力Rp表现为对流体流动的抵抗，它导致与压降相联系的能量损失。Rp为扬程-流量曲线的斜率，即Rp＝∂H/∂q。以大量全尺泵常规水试为基础进行统计分析，给出具有较高置信度和统计意义上的泵阻力值。根据泵的相似准则和水试数据，可得任意转速n时的泵阻力特性方程

式中：a1和a2为拟合系数；ρ为介质密度。

1.2 泵惯性

惯性Lp表示使流体加速或减速而引起的压力变化。根据介质在流道内的绝对运动轨迹长度和流道的等效截面面积进行计算

经计算发现，泵静止部分惯性所占比例很大（主要集中在涡壳段），惯性随转速、流量变化很小，计算时可按常量处理。

1.3 泵气蚀柔度

气蚀柔度Cb反映气泡体积随脉动压力变化的灵敏度

Cb对推进系统的模态频率有很大影响，对POGO现象是否发生及何时以何种频率发生等问题都有直接影响，是POGO稳定性分析的一个非常重要的参数。在流路中人为产生正弦扰流，在泵不工作和工作两种状态下输送管液路的同阶模态频率将发生变化，依据同一液压振型共振频率的差异来推算泵气蚀柔度（共振测柔法）。当泵前管液路谐振时，其一阶振型为1/4正弦波的开-闭振型。此时，隔离贮箱出口认为是纯开端，因泵终端阻抗相对于泵前抽吸系统的阻抗较大，故可认为泵端为理想闭端。

泵不运转、正弦扫频激励时，泵前管液路的一阶频率为f，此段管路系统的柔度为

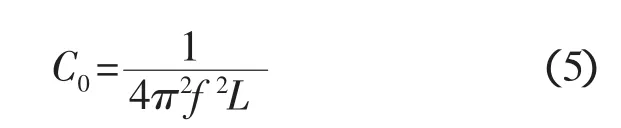
式中：L为隔离贮箱出口至泵入口流路的惯性。

泵运转、正弦扫频激励时，泵前管液路的一阶频率为f′，此段管路系统和泵的柔度为

由此可得泵的气蚀柔度

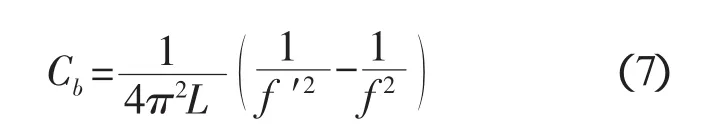
1.4 泵质量流量增益因子

质量流量增益因子Mb反映泵入口流量波动引起气泡体积的变化率（受诱导轮叶片攻角影响），即

当动力系统和结构系统的模态频率非常接近时，会降低系统阻尼而减小POGO稳定性裕度。通过泵入口、出口之间脉动压力、脉动流量之间的传递特性，可得

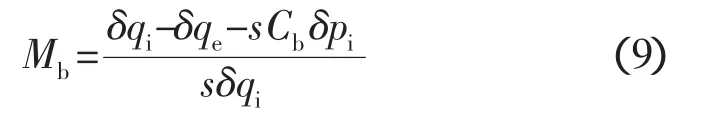
1.5 泵动增益

(m+1)反映泵对流体脉动压力的放大作用，其影响箭体耦合系统的POGO稳定性裕度。 (m+1)是从动态水试的速变数据中获得，而不是从稳态压头增量与入口压力的斜率中得出。

准静态增益

在有些文献中采用下面公式计算

式中：Zp和Zd分别为泵阻抗（Zp=Rp+sLp）和泵下游阻抗；δpe/δpi为泵压比。

上面的定义不够准确，决定由泵的传递方程导出泵动增益计算式

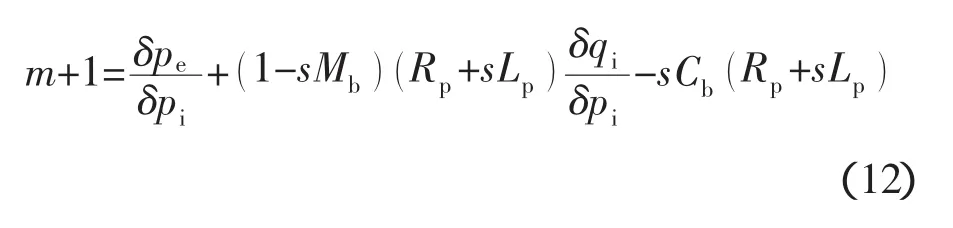
2 试验设计

2.1 试验系统

试验系统如图1所示。

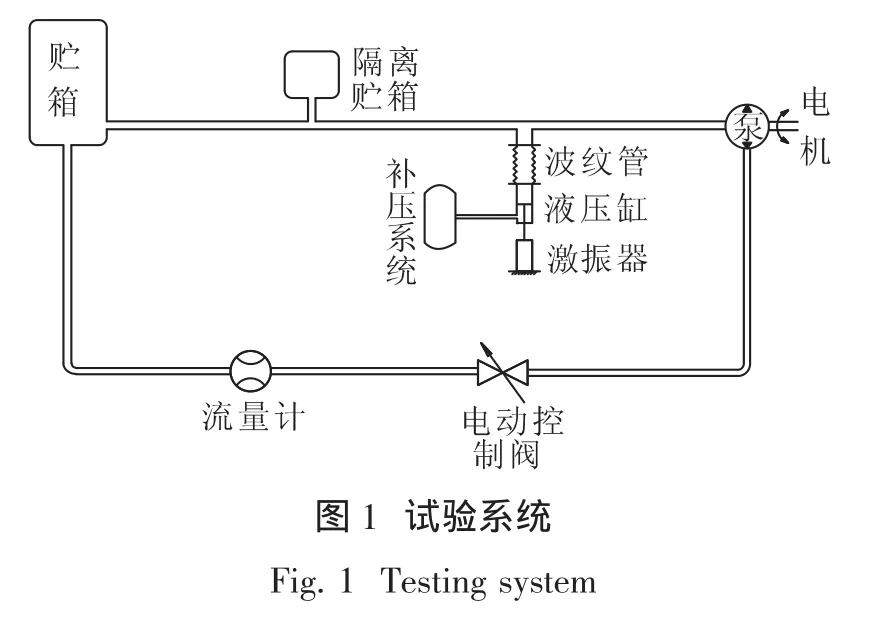
隔离贮箱的作用：①用于隔离上游供应系统的噪声，在贮箱出口形成一个近似“开”的边界；②简化试验系统，便于试验时判断贮箱→泵入口管路的液压振型及谐振频率。

为了在泵前管路形成一定量级的流量和压力激励信号，在泵入口安装激励系统。液压缸通过波纹管与主管路的三通连接，波纹管可补偿管路的长度和对中，还可隔离激振器和液压缸产生的机械振动。

通过增减水箱中的压力来调节管路中流体的压力。泵后电动调节阀用来调节流量，保证水试工况满足模拟准则。

2.2 模拟准则设计

由于试验条件所限，为尽可能模拟泵真实工况，采用以下模拟原则：

1）试验工况相似

泵水试时采用电机驱动，受电机功率的限制，泵最高可驱动到9 000 rpm，无法达到发动机额定转速。为了保证水试工况与发动机额定工况相似，应保证水试点与额定点处于同一条相似线上，即

式中下标w和0分别表示水试工况和额定工况。

2）气蚀裕度相等

下列因素导致水试与泵实际工作状态有较大差别：水试转速低于实际工作转速；水的饱和蒸汽压与液氧的饱和蒸汽压有较大差别，相应地影响到泵的气蚀特性。为了减小上述因素的影响，应保证水试转速下的泵气蚀裕度与实际工作状态相等，有

式中：ps0和psw分别为实际介质在额定工况下的饱和蒸汽压和水在水试条件下的饱和蒸汽压。

2.3 隔离贮箱设计

对于图2所示系统，左端为主贮箱，近似为理想开端，右端为泵，近似为理想闭端。隔离贮箱内气垫按绝热过程考虑。

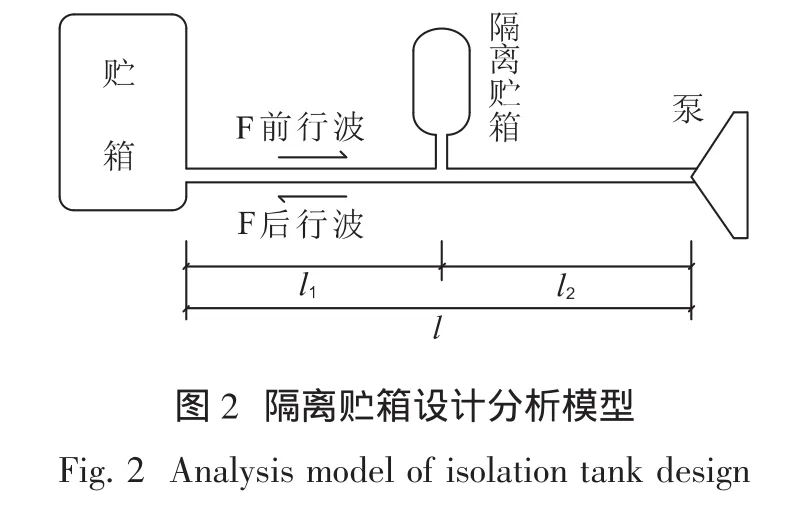
根据液压波动理论，隔离贮箱通过系数

式中：Zl=2l2f/a表示隔离贮箱距泵端的安装距离与半波长的比值；a，f为流体声速和频率；Zc为特征阻抗；导纳其中L和aRa分别为隔离贮箱连接管的惯性和流阻，Ca为隔离贮箱柔度。从式 (15)可以看出，增加隔离贮箱的柔度可以有效减小通过系数的模，从而起到隔离上游噪声的作用。另外，隔离贮箱的安装位置也对通过系数有影响，对于某一需要隔离的频率，隔离贮箱安装于半波长的整数倍位置（压力波腹）时通过系数最小，而安装于1/4波长位置时通过系数较大。

分析了隔离贮箱气垫体积Vg和贮箱连接管长度l′对S的影响。对于较高频率的噪声，为获得较好的隔离效果需要的Vg较小；而对较低频率的噪声，为获得较好的隔离效果需要的Vg大；对不同频率的噪声，增大Vg总可以减小S，这是因为随Vg的增大，其容抗减小，从而起到吸收脉动压力的作用。连接管的惯性对隔离贮箱的滤波效果有很大影响，连接管路越长，惯性越大，隔离贮箱的滤波效果越差，直接连入主路最好；因此，在试验台允许的情况下，应尽量减小l′。

隔离贮箱的引入相当于在管路中加入了一个集中流容元件。此流容足够大时，可使隔离贮箱出口的阻抗很小，从而接近于一个开端。因此，对隔离贮箱的设计要求为：①最小的惯性和流阻；②Vg较大且可调。

2.4 激励系统选型

由于试验管路管径较大，采用脉动阀扰动无法实现，故在泵入口管路上设计了液压激振系统。为满足泵的线性化条件和气蚀标准，应使泵的动态特性独立于激励水平和激振位置，所激起的脉动压力幅值要尽量小。同时，为了保证测试信号具有高信噪比，要求脉动压力幅值水平足够高。压力振荡水平取决于活塞处输入脉动流量的幅值、试验系统及流体声速等。

2.4.1 行程计算

为保证所测量的脉动压力信号有足够高的分辨力和信噪比，激振系统应能在要求的频率范围内激励起大约10%静压的脉动压力。分析模型如图3所示。依据边界条件：z5=0，z4=∞；根据流体动力学传递关系有行程计算式

式中：Re，Le和Ce分别为激振系统支路的阻力、惯性和柔性；As为活塞有效面积。

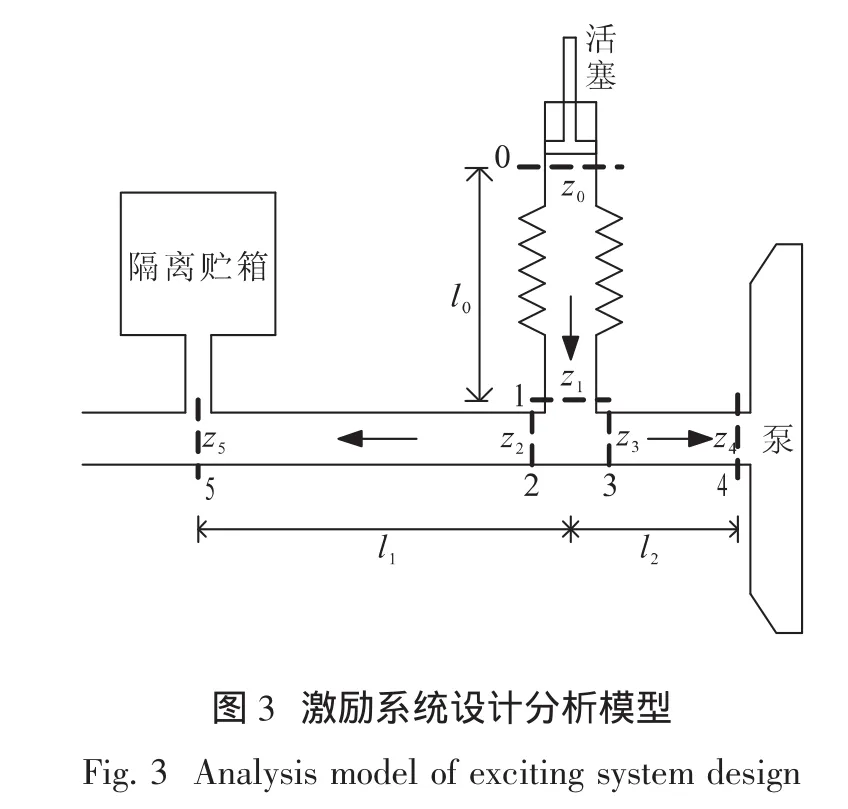
随激振频率的升高，活塞行程将减小且在谐振频率处所需行程最小。

2.4.2 激振力计算

对激振器进行受力分析以确定激振器的静动力大小，作用于活塞的总力为

式中：Fp，Fd，Fm和Ff分别为静压作用力的合力、瞬态液动力、惯性力和摩擦力，Fd=sωρl0AsX。

2.4.3 激振器选型

选用美国Xcite System Corporation的液压激振器Xcite 1200-6 System。

2.5 控制和测量分析系统

采用OROS 38系统进行速变数据的采集及分析，控制和测量分析系统如图4所示。

3 试验内容

在试验测试中采用了“示踪”信号发生器技术，采用该方法可对所采集的信号进行“示踪”或“标识”，为数据的分析工作带来很大的方便。

为了保证各试验系统协调工作，摸索激励系统、隔离贮箱及测量分析系统等的性能和影响，并对试验方案进行可行性评估，将试验分为预备性试验和正式试验两个阶段。

预备性试验中考虑到试验的安全性和为排除试验管路结构模态对流体模态（目标频率）的干扰，进行了结构模态试验。进行隔离贮箱滤波效果试验、激励系统特性试验、泵不运转状态激励试验，可验证试验方案，检验预分析结论，对激励参数进行探索及对激励方式、测量装置、数据处理方法和信噪比进行评价等。

正式试验是对管泵组成系统进行水力学脉动试验，研究输送管路的水力学共振特性和泵的流体动力学传递特性等。在不同增压量级下，进行了宽频白噪声激励、宽频正弦粗扫描激励、窄带正弦精扫描激励和定频激励。

4 数据处理方法

4.1 传递函数选择

根据试验系统的输入、输出变量可建立多种传递函数，并通过传递函数来确定液路模态。理论分析和试验表明，并非所有的传递函数都能正确给出系统特征频率，这就必须选择恰当的传递函数。简化泵前管路系统，见图5。

以活塞加速度作为输入变量，系统特征频率为

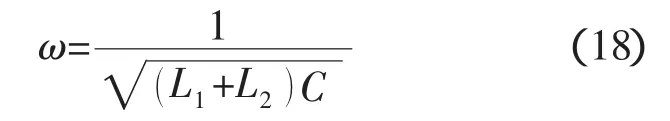
式中：C为系统柔性；L1和L2分别为l1和l2段的惯性。当以活塞处激振压力作为输入变量，系统特征频率为

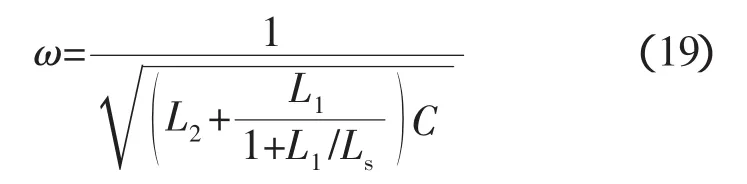
从式（18）可以看出，以活塞加速度作输入变量的传递函数δp2/as可以给出正确的系统特征频率。由式（19）可得，只有当ls段惯性Ls>>L1时，才能得到正确的系统特征频率。由于在试验设计时，Ls较小，因此以活塞激振压力作为输入变量的传递函数δp2/δps不适合此次试验数据分析，而选用δp2/as作为本次泵POGO试验数据处理的传递函数。

4.2 液压共振判别

流体系统共振的判别方法可采用阻抗分析法、响应峰值法和矢量分析法，本试验采用了以下两种液压共振判别方法：①共振法：用正弦扫描求响应的方法，当激励频率接近耦合频率时，系统产生共振峰值响应。②传递函数法：在随机、正弦扫描激励的情况下，用激励点与响应点的传递函数来确定；当传递函数的频谱出现峰值时相位接近90°或270°，相干系数接近1或其虚部最大而实部为零的，采用液压共振的特点来判定是否发生谐振。

4.3 脉动流量推算

在流路夹气严重的区域（如泵入口低压区），由于流体中气泡的扩散、折射，激光Doppler速度计（LDV）、电磁流量计（EMM）和超声波流量计对脉动流量不能进行准确测量。另外，上述流量计价格昂贵，装拆及测量要求较高，流量计的检定也是一个大问题。而普通流量计由于频响原因，无法满足测量脉动流量高采样率的要求。鉴于以上原因，本文采用了一种依靠两测点脉动压力推算脉动流量的新方法。借助于两测点所测得的脉动压力，依据小扰动假设下的无粘流直管流体动力学传递关系得到脉动流量，有

5 动态水试结果及分析

5.1 泵前管液路一阶模态

泵不工作和工作时，泵前管液路的一阶模态频率f1如图6和图7所示。

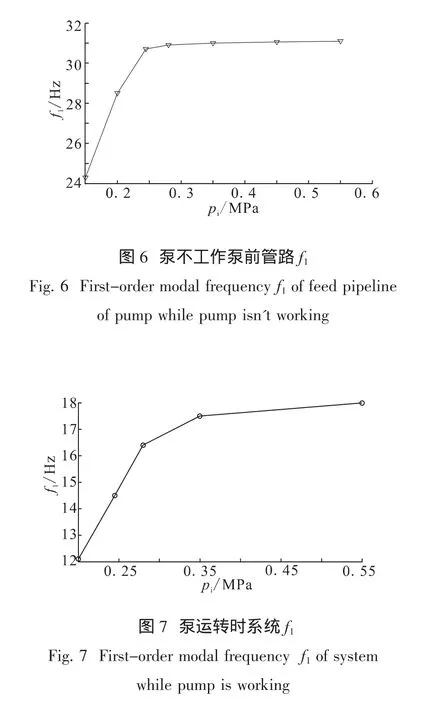
可以看出f1随管路充压pi的增大而增高，特别是在低压区，充压状态对系统谐振频率影响很大。泵运转时f1比泵不运转时低很多，随pi的变化规律与泵不运转时基本保持一致。在信噪比较高的情况下，为了保证试验数据具有较好的线性度，选择小激振力精扫试验所得的结果作为计算Cb的依据。

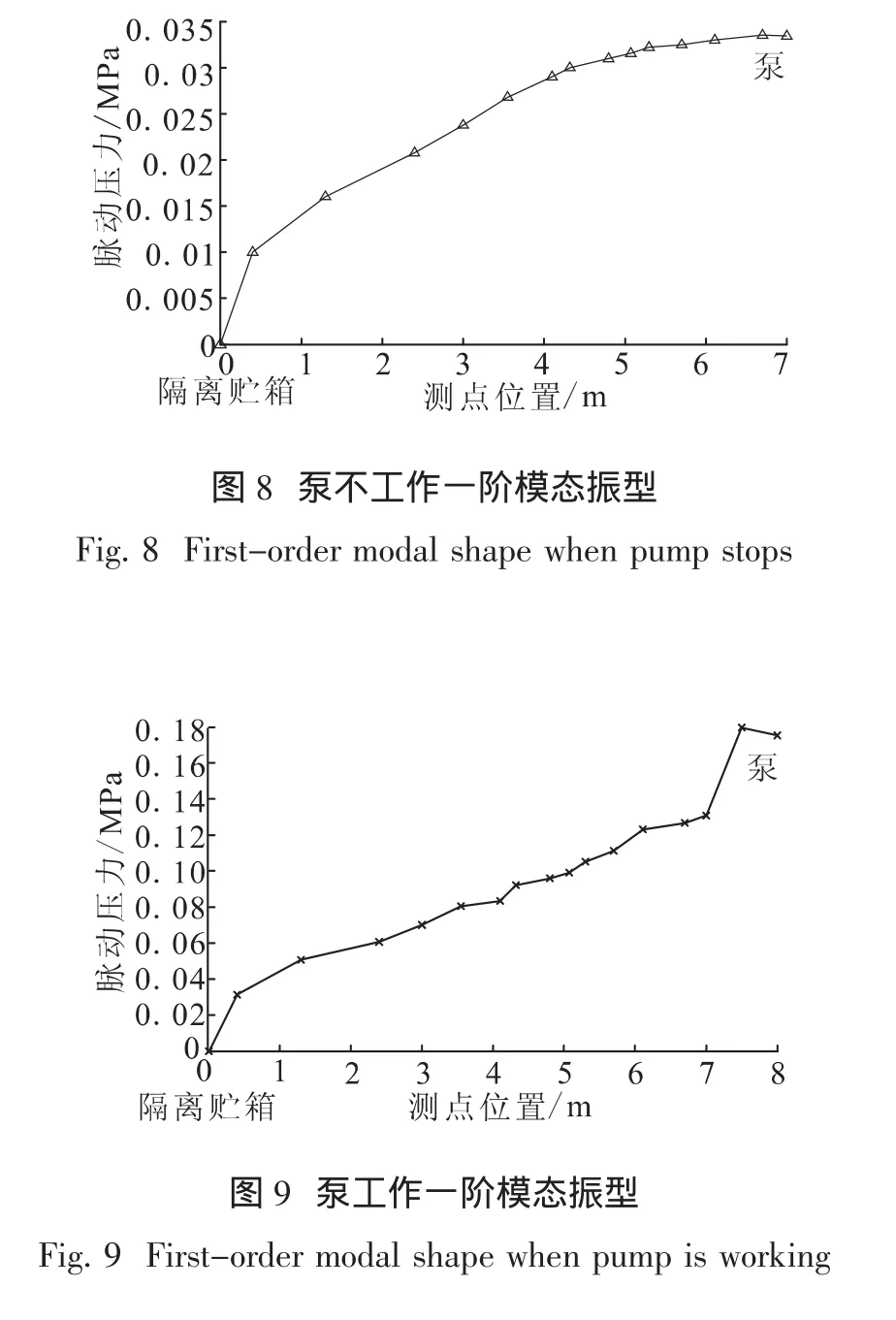
当泵不工作时，得开-闭管的一阶液压振型（λ/4），见图8。一阶压力谐振时，各点压力脉动矢量方向相同。隔离贮箱处的脉动压力接近于0，说明隔离贮箱具有良好的滤波效果；泵端处的脉动压力最大，可近似为理想闭端。

当泵工作时，隔离贮箱→泵入口也可近似为开-闭管（见图9），泵对脉动压力起放大作用。

5.2 气蚀柔性

采用正弦扫频激励寻找到目标频率，求得5个充压状态下的Cb，见图10。随着泵前压力的减小，泵气蚀加剧，气蚀系数K越小，Cb急剧增大，并具有较好的规律性。

5.3 质量流量增益因子

利用式（9）可得Mb，Mb随频率的增高迅速减小，随气蚀数K的减小而减小。

5.4 动增益

在不同入口压力及不同激振频率下的动态增益是通过定频激振试验获取的， (m+1)和泵压比δpe/δpi随入口压力及激振频率变化关系见图12。

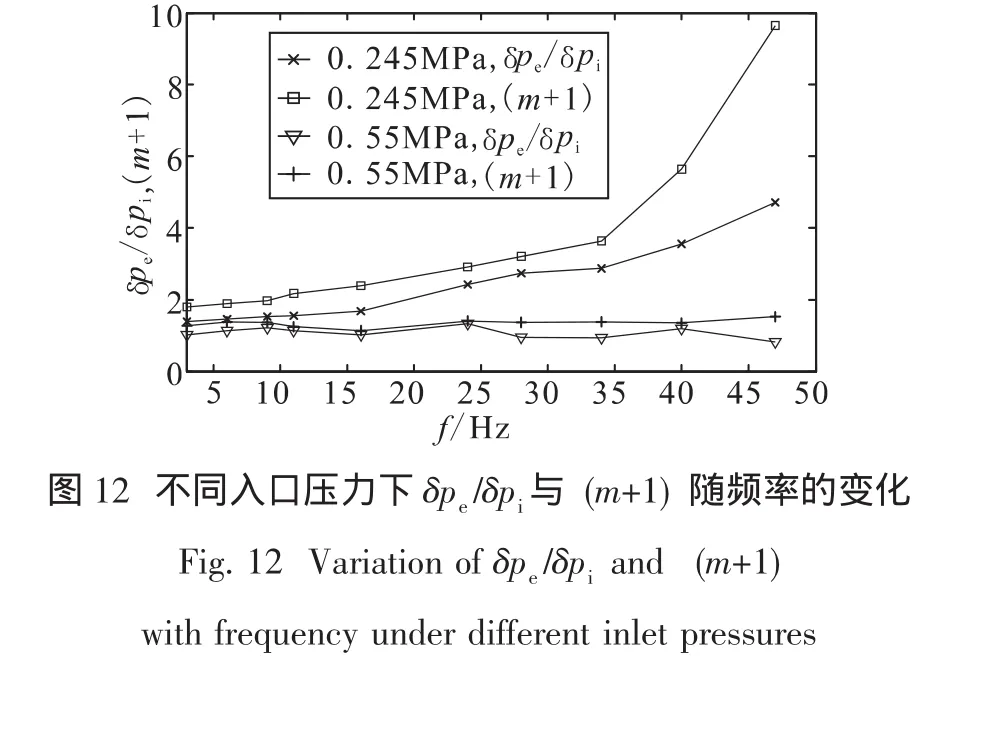
压力为 0.245 MPa 时，δpe/δpi值在 1.5～4 之间，(m+1)的值在2～10之间，整体趋势为随频率值增大而增大。在0.55 MPa压力状态下δpe/δpi的值在0.7～1.4之间波动，(m+1)的值在1～1.6之间。从δpe/δpi和 (m+1)的变化趋势可以看出，泵动增益随入口压力增大而减小。δpe/δpi与(m+1)差别很大，由此可见仅用δpe/δpi值来表示泵动态增益并不准确，而动增益更能准确地描述泵的流体动力学传递关系。

6 结论

通过对某型发动机氧泵的POGO动态水试，获取了泵关键动特性参数及参数的规律特性。泵入口压力pi在0.2～0.55 MPa范围，无量纲Cb的大小在1.2～6.5之间，且随pi的增高而减小。Mb随压力的变化不明显，但随频率的增高迅速减小。 (m+1)变化的总体趋势为随pi的增高而减小；当 pi为0.245 MPa时， (m+1)随频率的增高而增大；当pi为0.55 MPa时， (m+1)随频率的增高基本保持不变。

[1]OTSUKA S,TSUJIMOTO Y,KAMIJO K,et al.Frequency dependence of mass flow gain factor and cavitation compliance of cavitating inducers[J].Journal of Fluids Engineering,1996(6):400-408.

[2]DOTSON K W,RUBIN S,SAKO B H.Effects of unsteady pump cavitation on propulsion-structure interaction(POGO)in liquid rockets,AIAA2004-2027[R].USA:AIAA,2004.

[3]RUBIN Sheldon.An interpretation of transfer function data for a cavitating pump,AIAA2004-4025[R].USA:AIAA,2004.

[4]SHIMURA Takashi.Geometry effects in the dynamic response of cavitating LE-7 liquid oxygen pump[J].Journal of Propulsion and Power,1995(2):330-336.

[5]IACOPOZZI M,LIGNAROLO V,PREVEL D.POGO characterization of ARIANEⅤturbopump LOX pump with hot water,AIAA 93-2124[R].USA:AIAA,1993.