轻型火炮后大架结构分析与优化

邵跃林，顾克秋，周成

(南京理工大学，a.机械工程学院;b.工程训练中心，江苏南京 210094)

0 引言

现代战争要求火炮具备快速反应能力，结构轻量化因此成为火炮设计的一个重要发展方向。

基于先进设计理论与方法的炮架结构优化设计是火炮轻量化技术中具有意义的课题。

文献［1］应用结构优化技术对某迫击炮坐钣进行强度和质量的多目标优化，获得了强度高、质量轻的坐钣结构。文献［2］对某炮尾齿形结构参数化建模，并在此基础上对炮尾的刚度和强度进行多目标优化，使炮尾的刚强度均有所提高。

本文以某轻型火炮后大架为研究对象，首先建立后大架与土壤接触的有限元模型分析后大架的强度，然后在分析结果的基础上，合理地简化有限元模型，用弹簧连接器替代土壤，建立用于寻优计算的集中参数有限元模型。以后大架的形状参数和板厚参数作为优化设计变量，采用改进的非支配排序遗传算法(NSGA—II)对后大架的最大应力和质量进行多目标优化。

1 后大架结构有限元分析

1.1 后大架结构与受力模型

后大架在火炮中与下架后支臂通过两个销轴连接，可以分为架体和驻锄两部分。在火炮的射击过程中，后大架受到来自下架后支臂的水平方向力F，通过驻锄将力传递给土壤，土壤产生弹性和塑性变形，吸收能量，除此之外，后大架还受到自身重力的作用，这些力使后大架产生向后的平动和绕驻锄的转动，后大架结构与受力如图1。

图1 后大架结构与受力

1.2 后大架－土壤有限元模型

后大架采用一阶完全积分壳单元离散，下架后支臂采用刚性的梁单元模拟;下架支臂与后大架之间采用转动副连接;下架支臂与地面之间采用弹簧连接器连接模拟全炮质量对火炮跳高的影响，弹簧连接器刚度等于全炮重量与跳高的比值;驻锄与土壤之间定义接触;在下架支臂前端施加水平方向的集中力F。

火炮在密实砂土条件下射击时，与后大架接触的土壤被压实，几次射击后，砂土紧密结合在一起，本文分析此种工况下后大架的强度。土壤采用Mohr-Coulomb本构模型，特性参数如下:弹性模量30 MPa，泊松比0.3，孔隙比0.55，内摩擦角 35°，剪胀角 10°。

为了准确模拟后大架驻锄与土壤的相互作用，本文对土壤进行离散，在土壤的人工边界上建立无限元(IFEM)作为土体的边界条件，采用有限元-无限元耦合的方法模拟土壤半无限空间体。综合考虑计算成本和计算精度，土壤模型有限元部分采用一阶四面体单元模拟，土壤边界采用八节点空间无限元模拟［3］。后大架-土壤有限元模型如图2。

图2 后大架－土壤有限元模型

1.3 计算结果分析

应力和变形如图3所示，其中变形图系放大30倍的效果。可见后大架最大应力593.3 MPa，出现在驻锄背面的加强筋上，除去应力集中区，其他大部分区域应力均小于200 MPa。

后大架驻锄与土壤接触后，后大架压缩土壤向后的运动可分解为平动与转动两部分，这一运动趋势与火炮发射的实际情况是相符合的。

计算结果显示后大架应力分布并不均匀，其结构有优化的空间，可以通过对后大架架体形状优化、驻锄加强筋布局优化以及板厚参数优化减小后大架最大应力，减轻后大架质量。

2 后大架结构优化

2.1 结构优化方法

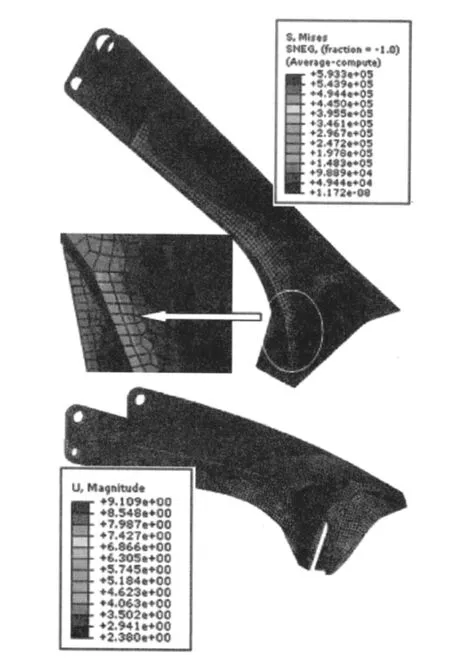
图3 后大架应力变形图

现代结构优化大多基于有限元法，主要包括尺寸参数优化、形状优化、拓扑优化等。尺寸参数优化方法通过合理匹配结构的外型尺寸等参数，获得较好的结构形式;形状优化通过优化节点位置分布，获得较好的局部形状，避免应力集中;拓扑优化包括变密度法，渐进结构优化法等，变密度法引入材料插值模型，给予每个单元一个虚拟的密度值映射材料的弹性模量与泊松比，通过寻优计算改变单元密度，保留高密度区域，去除低密度区域获得传力效果最佳的结构［4］。上述方法中，尺寸参数优化方法理论上已经完善，在工程领域获得了广泛的应用，但在优化结构形状与布局方面能力有限，形状优化方法和拓扑优化方法尚处于理论完善阶段，在处理复杂的工程问题方面仍有所欠缺。

现代火炮架体多采用薄壁焊接结构，结构主要参数包括板材厚度参数和外形尺寸参数等。本文采用尺寸参数优化方法，将后大架的板厚参数和外形尺寸参数共同优化，不仅能实现板厚的合理匹配，也能实现后大架架体的形状优化和驻锄加强筋的布局优化，在一定程度上实现了形状优化和拓扑优化的功能。

2.2 后大架集中参数有限元模型

由于寻优计算需重复进行多次有限元分析，必须严格控制计算时间。1.2条提出的后大架-土壤模型计算时间较长，无法满足优化计算要求。本文在1.2条的基础上，提出一种简化的集中参数有限元模型，使该模型计算结果与后大架土壤模型近似。该模型可以大大提高计算效率。

集中参数有限元模型建立方法如下:首先在驻锄附近建立节点模拟驻锄的转动中心，将该节点与驻锄面耦合，然后建立固定的节点模拟地面，给两个节点间赋予刚度，用两个节点的相对位移模拟土壤的变形。

建立集中参数模型的关键在于给出与驻锄面耦合的节点位置，该节点本质上为驻锄的转动中心点，本文通过计算给出这个节点的大致位置。

驻锄变形前后的位置如图4。点M(a，b)和M’(c，d)分别为变形前后驻锄上的对应的两点，坐标O(x，y)为转动中心点。与外加载荷相比，驻锄质量可以忽略不计，其竖直方向下沉量几乎为O，可以认为由M点到M'点其y方向坐标的变化完全是由驻锄转动引起的。由刚体运动学知识可知，变形前后驻锄绕转动中心点(x，y)的转角即为驻锄上任意一条边变形前后的转角φ。建立局部坐标系如图4所示。O，M，M'位置满足以下关系:

其中a，b，c，d，φ 为已知数。

式(1)可保证驻锄的运动关系，通过数学软件求解可以得到一条满足上式的曲线。经试算可在上述曲线上找到一点与驻锄面耦合，使后大架最大应力约等于1.3条计算结果。该点同时满足运动关系和应力关系，即为本文需要寻找的转动中心点。

图4 驻锄变形情况

2.3 后大架的参数化模型

用python语言编写有限元前处理程序实现后大架的参数化建模，参数主要分为板厚参数和形状参数两大类，改变这些参数值即可获得不同的后大架模型。使用a，b，c三个参数可控制后大架架体形状，d，e两个参数可控制驻锄加强筋的布局，如图5所示。

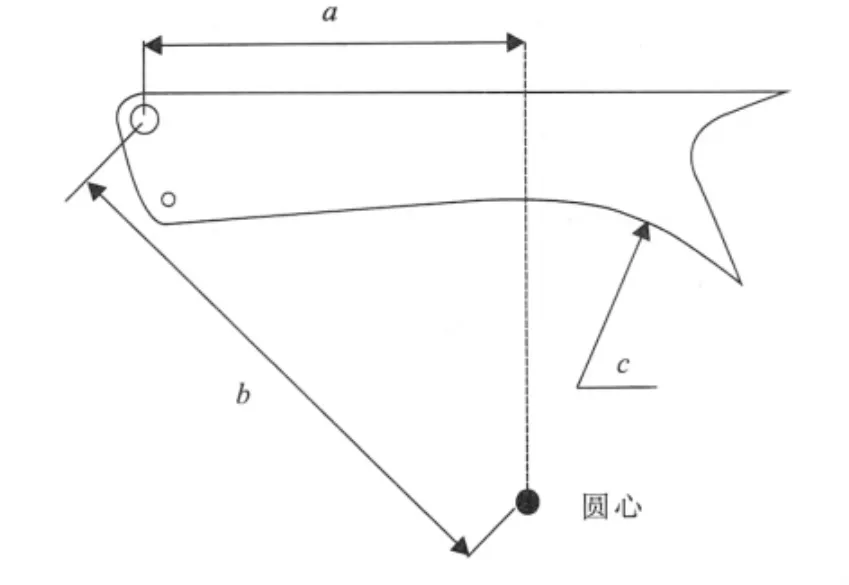
图5 后大架模型主要形状参数

后大架不同部分受力情况不同，所取板厚也不同，后大架是由型材焊接而成，板厚参数取整数，形状参数取实数。所有参数及取值范围如表1所示。

表1 优化设计参数表

2.4 后大架多目标优化的数学模型

优化模型以后大架形状和板厚参数为设计变量，材料许用应力为约束条件，后大架质量和最大应力为设计目标，目标函数如下:

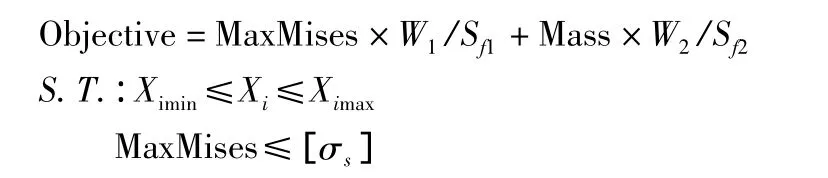
其中MaxMises为后大架最大应力，Mass为后大架质量，Xi为设计参数，包括后大架形状参数和板厚参数共11个参数，［σs］为材料许用应力，这里取500 000 KPa。

W1和W2为属于变量的权重因子，体现在本次多目标优化中不同优化目标的重要性，Sf1和Sf2为属于变量的比例因子，作用是统一不同的目标函数值的数量级。

2.5 优化算法

改进非支配排序遗传算法(NSGA-Ⅱ)是基于Pareto最优概念的多目标遗传算法。多目标优化问题与单目标优化的区别在于不存在唯一的全局最优解，而是存在一系列解，其特点为至少存在一个目标优于其他所有的解，这样的解称之为Pareto解，这些解的集合即为Pareto最优解集［5］。

NSGA-II算法中，选择较大的种群数和进化代数更容易获得全局最优解，但是计算时间会随之增加，较大的交叉概率可以获得较快的收敛速率，但过大的交叉概率可能会导致早熟现象。综合考虑各种因素，本次优化的种群规模取50，进化代数取65代，交叉概率0.9。

3 优化结果分析

通过优化计算得到后大架质量和最大应力的Pareto最优解集，Pareto前沿面如图6。

图6 后大架最大应力－质量Pareto前沿面

经多目标优化，后大架质量和后大架最大应力均有所下降。从Pareto前沿面上选择了三个点A，B，C和原方案进行比较，最大应力和质量如表2。

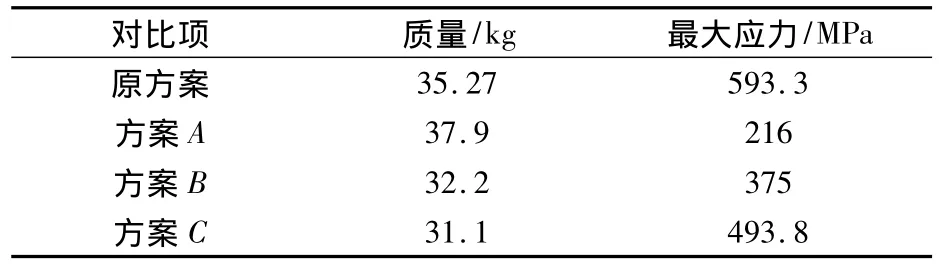
表2 后大架优化方案结果对比

与原方案相比，方案A后大架最大应力大幅下降了63.6%，后大架质量上升了7.46%;方案B最大应力下降了36.8%，质量下降了8.7%;方案C最大应力下降了16.8%，质量下降了11.82%。方案A应力大幅下降是以质量上升为代价的，方案B质量和最大应力均有所下降，方案C质量下降最多，最大应力接近材料许用应力，可见质量和最大应力是一组矛盾的值，必须根据实际情况选择最合适的方案。

4 结语

首先建立了后大架-土壤有限元模型分析后大架强度，在分析结果的基础上，使用集中参数模型替代土壤模型建立用于寻优计算的有限元模型，应用多目标遗传算法NSGA-II进行了后大架强度和质量的多目标的优化，得到后大架模型的一组Pareto最优解集，使优化后的后大架质量和最大应力均有不同程度的下降。该组Pareto最优解集为后大架结构设计提供了参考，同时，本文所使用的方法对薄壁焊接结构的优化设计也有一定的借鉴意义。

［1］马洪锋.迫击炮座钣结构分析与优化设计［C］.南京:南京理工大学，2009:19-29.

［2］彭迪，顾克秋.基于响应面法的三维炮尾结构设计优化［J］.计算机辅助工程，2010(4):91-98.

［3］朱向荣，王金昌.ABAQUS软件中部分土模型简介及工程应用［J］.岩土力学，2004(25):144-148.

［4］荣见华，张强，葛森，等.基于设计空间调整的拓扑优化方法［J］.力学学报，2010(3):256-267.