板格形导管架桩基码头稳定性简化计算方法
2013-10-13张连丽王元战
张连丽,王元战,陈 飞
(1.天津大学水利工程仿真与安全国家重点实验室,天津 300072;2.天津市港口与海岸工程重点实验室,天津 300072;3.交通运输部规划研究院,北京 100028)
板格形导管架桩基码头是适用于深水软土地基的新型结构,主要由预制的板格形导管架拼接而成,通过竖向导管打入基桩形成桩基础,如图1所示。穿过导管打入基桩,增强地基承载力,有效提高结构稳定性。该结构整体性好、自身重量轻、工程造价低、施工简便,在我国长江口、珠江口及渤海湾等淤泥质海岸地区具有广泛的应用前景。但该码头承载特性与破坏模式尚不明确,稳定性计算方法尚无规范可循,因此对该结构稳定特性及计算方法的研究具有重要意义。
目前,适用于软土地基的新型结构主要有沉入式大圆筒结构、箱筒型结构,格型钢板桩结构等,这些结构在工程中已得到应用。文献[1-3]介绍了沉入式大直径圆筒结构稳定性简化分析模型,给出四种计算方法;通过ABAQUS软件,建立了稳定性分析的有限元模型。文献[4-5]对箱筒型基础结构稳定性进行研究,建立简化计算方法,并与有限元结果进行比较。文献[6-7]分别采用理论分析方法——“修正分离法”及ABAQUS有限元数值分析方法,对格形钢板桩结构稳定性进行研究,比较不同土质、不同入土深度下格形钢板桩结构的极限承载力。板格形导管架桩基码头结构的作用机理和承载特性不同于上述结构,关于其稳定特性及分析方法,尚无公开发表的文献。
以板格形导管架桩基码头单个构件作为分析对象,以前排桩轴线上(导管架底部以下L深度处)一点作为假想支撑点,建立基于该转动点的稳定性简化分析模型。除结构自身重量外,还应考虑板格型导管架与周围土体间摩擦力,桩侧摩阻力、桩侧水平土抗力等,对结构进行极限状态受力分析,建立水平方向及基于转动点的力的平衡方程,并通过强度折减法确定结构稳定性安全系数。通过ABAQUS软件建立三维弹塑性有限元分析模型,并与简化方法进行比较。结果表明简化方法与有限元法吻合度较高。
1 码头结构型式
板格形导管架桩基码头作为新型港工结构,由预制的板格形导管架和桩基组成。板格形导管架由前纵板、后纵板、纵隔板与横侧板、横隔板相互交叉连接而成,于横侧板与前、后纵板交接处设置竖向导管。预制构件吊至现场并排安放,根据稳定性要求将其沉入土中一定深度,通过竖向导管打入基桩形成桩基础,基桩与导管间缝隙用混凝土浇筑,从而使二者连成整体,如图1(a)所示。板格形导管架空腔内填充砂或块石,并于上部浇筑混凝土盖板、钢筋混凝土胸墙、门机轨道纵梁等构件,整个码头断面见图1(b)。
重力式码头结构主要依靠自身重量维持稳定性,在抗倾稳定性计算中,结构绕前趾点发生转动。对于板格形导管架桩基码头,导管架入土较浅且底部处于软土地基,无法对结构起到支撑作用,而基桩可穿过软土层达到持力层。当结构向海侧发生转动时,假定前桩(临近海侧的基桩)成为支承,以使重心对其产生稳定力矩,维持结构稳定特性。

图1 板格形导管架桩基码头Fig.1 Plate panel type wharf with jacket and pile foundations
2 结构稳定性简化计算模型
以板格形导管架桩基码头单个构件作为稳定性分析对象,如图2所示。为了便于计算,忽略悬臂端长度,假定导管架陆侧面、海侧面均为直立平面,由此分析模型进一步简化为如图3所示的矩形平面。关于板格形导管架内部填料,可借鉴沉入式大直径圆筒结构稳定性分析思路,将板格形导管架结构与内部填砂作整体考虑,其中内部土体取一定比例的有效重量。

图2 结构平面示意Fig.2 Plan layout of the structure

图3 简化平面示意Fig.3 Simplified plan layout
建立构件抗倾稳定性分析模型,如图4所示。假定码头失稳模式为绕导管架底部以下一定深度处前排桩轴线上某点发生转动。在分析抗倾稳定性时,考虑的竖向作用力主要包括结构重力G,外部土体对导管架两侧的摩擦力T1、T2,桩侧摩阻力T3、T4,桩底端土反力R,门机荷载PP1、PP2;水平作用力包括陆地侧填土对导管架结构产生的主动土压力P1,前方堆货荷载产生的主动土压力P2,临海侧导管架入土段承受的被动土压力P3,导管架底部受到的水平切力T,桩侧土抗力PS1、PS2。假定码头处于有掩护水域,波浪力不作考虑。
结构重力G包括板格形导管架桩基构件自重Gb、导管架空腔内部填砂重Gs、结构上部胸墙、门机轨道纵梁以及填砂产生的竖向力Gu。其中,腔内土体重量取抗倾稳定的有效重量,定义系数η为起抗倾作用的有效填砂重量占腔体填砂总重量的百分比,则重力G的表达式为:

图4 结构稳定性分析简化模型Fig.4 The simplified model for stability analysis

其中,η的数值按照《重力式码头设计与施工规范》[9]中关于无底空心方块码头腔内填料抗倾重量的计算公式确定,结合大圆筒结构抗倾稳定性分析[1],取板格内土体重量的70%作为抗倾稳定性分析的有效重量(即η=0.7)。
陆侧土体对导管架外壁的竖向摩擦力T1(方向竖直向下)表达式为:

式中:f1为泥面以上z处回填砂对导管架外壁单位面积的竖向摩擦力;f2为泥面以下z处软粘土对结构单位面积的竖向摩擦力;H为导管架泥面以上高度;t为导管架泥面以下高度;D为单个构件宽度。
海侧土体对板格形导管架外壁的竖向摩擦力T2(方向竖直向上)表达式为:

桩侧摩阻力数值表达式为(T3方向向下,T4方向向上):

式中:n为单个构件前排桩(或后排桩)的根数;Aci为某一土层桩侧与土体的接触面积;fi为某层土体对桩侧单位面积上的摩擦力,根据美国API规范[8],fi不大于该层粘土不排水剪切强度Cu,最大可取Cu。
桩端土反力R可由下式求取:

式中:Ad为桩底与土体接触面积;根据API规范,粘性土最大端阻应力取9 Cu。
陆地侧后方填土对板格形导管架的主动土压力P1、前方堆货荷载产生的主动土压力P2可根据《重力式码头设计与施工规范》[9]进行计算,单位宽度土压力分布按郎肯主动土压力公式计算:
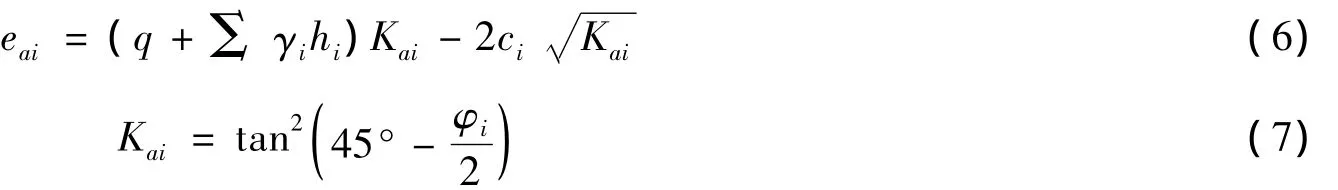
其中,γi为不同土层土体重度;hi为对应土层深度;q为墙前床面均布荷载(kPa);Kai为主动土压力系数,φi为土体内摩擦角(°),ci为土体粘聚力(kPa)。
海侧土体对结构的被动土压力P3可通过郎肯被动土压力计算公式求得:

板格形导管架底部受到的水平切力T极限值为:

式中:B为板格形导管架宽度,cu为导管架底部土层不排水剪切强度。
作用于前后排桩上的门机荷载Pp1、Pp2可根据《港口工程荷载规范》[10]求取。在非往复荷载作用下,若粘土不排水剪切强度标准值小于96 kPa,可按下列公式计算桩侧单位面积极限水平土抗力值[11]:

式中:pu为泥面以下某深度处桩侧单位面积极限水平土抗力标准值(kPa);cu为粘土不排水抗剪强度(kPa);γ为土体重度(kN/m3);Z为泥面以下任一深度(m);d为桩径或桩宽(m);J为系数,取0.25~0.5;当极限水平土抗力不再随深度增加而变化时,此处深度记为ZR,其计算公式为

故而桩侧土抗力Ps1,Ps2为

式中:hz为桩基入土深度。
3 稳定性分析方法
强度折减法是在外荷载保持不变的情况下,通过调整土体抗剪强度折减系数进行稳定性分析的一种方法,目前已被广泛应用于边坡稳定性分析[12-14]。抗剪强度折减系数定义为:在外荷载保持不变的情况下,土体发挥的最大抗剪强度与外荷载所产生的实际剪应力之比,即外荷载所产生的实际剪应力应与抵御外荷载所发挥的最小抗剪强度(按实际强度指标折减后的强度)相等。
采用强度折减法对板格形导管架桩基码头稳定性进行分析,并求取安全系数。其基本步骤为:
1)将土体强度指标c、φ同时进行折减,得到c'、φ'作为新的材料参数,分别由式(15)、(16)求得。土体重度、弹性模量、泊松比在计算时设为定值,不随c、φ值的变化而变化。

式中:Fr为强度折减系数。
我们常坐着读书、写作,坐着学习、吃饭、看电视等,似乎每天都处在“坐”的状态,原先的“蹲”被渐渐取消,并一直认为“蹲”不雅观、不高贵。殊不知,“蹲”是一种集运动和娱乐于一身的活动,也是锻炼的好方式之一。
2)将新的材料参数 c'、φ'值代入到式(2)~(14)中,得到新的荷载 T1',T2',T3',T4',R',P1',P2',P3',T',P'S1,P'S2。当Fr增大时,c'、φ'值减小,主动土压力 P'1、P'2增大,被动土压力、摩阻力及桩侧土抗力减小,直至结构达到临界失稳状态,此时Fr为安全系数。
3)当结构达到临界失稳状态时,水平力及转动点的力矩平衡方程为:

式中:l1、l2、l3分别为P1、P2、P3作用位置距导管架底部的竖向距离,可根据主被动土压力分布求得;ln为前后桩轴线间距离、lm为前桩轴线到陆侧导管架外壁间距离,均与结构尺寸有关,为常量;M's1,M's2为桩侧土抗力P'S1,P'S2对转动点产生的力矩,与L有关。两个非线性方程具有两个未知量Fr、L,通过Fortran编程进行迭代求解,即可得到强度折减系数Fr,即稳定性安全系数。
4 算例
4.1 结构基本尺寸
结构断面及平面示意如图1(b)、图2所示,主要构件尺寸确定如下。
1)板格形导管架宽度由码头的稳定性决定,综合考虑门机轨距及门机与码头前沿距离,确定垂直于码头方向的导管间距B为10.6 m,悬臂端B1为1.5 m;
2)参考《重力式码头设计及施工规范》中沉箱码头设计规定,板格形导管架内纵隔板间距b取3.2 m,横隔板间距s取3 m;隔板厚度不宜小于200 mm,纵、横侧板厚度不宜小于250 mm,故图2中a1取400 mm,a2取300 mm,a3取450 mm,单个构件长度D为10.1 m;
4)导管架结构根据《重力式码头设计及施工规范》,选择标号为C30的钢筋混凝土材料。
4.2 水文地质条件
选取天津港地区的水文地质条件,如表1所示。

表1 水文条件Tab.1 Hydrological conditions

图5 工程地质剖面示意Fig.5 Engineering geological sections
考虑到极端高水位为5.88 m,板格形导管架上部胸墙应满足高度要求,并取设计低水位作为不利情况分析码头结构稳定性。
采用天津港的地质资料,如图5所示,该段地质由上而下依次为淤泥层、淤泥粘土层、粉质粘土层、粉土层和粉砂层。选择N38钻孔断面,各层具体参数见表2。考虑设计船型的需要,码头前沿水深需满足船舶满载吃水,故挖除3.5~4 m淤泥。

表2 各土层主要参数Tab.2 Properties of soil layers
4.3 有限元计算模型
以上述结构尺寸及水文地质条件为算例,利用ABAQUS软件建立有限元模型,并采用强度折减法进行稳定性分析。根据结构的空间对称性,取构件的一半及前后一定范围的地基土体作为有限元计算区域,如图6所示。在水平方向上,土体计算域向两侧各取板格形导管架构件长度的5倍,在竖直方向上,土体深度取桩基入土深度的2倍。导管架左右两侧采用对称约束,地基表面为自由边界,底面为固定边界,前后侧面为侧限边界,左右侧面为对称边界。

图6 有限元计算域示意Fig.6 Elevation of finite element calculation domain
三维有限元模型的土体与结构均采用八节点三维减缩积分实体单元,在结构与土体相互作用区域(板格型导管架内外壁、导管架底面、基桩与土体接触区域)建立主从接触面。接触面本构模型在切向方向采用库仑摩擦本构模型,法向采用硬接触方式。由于板格形导管架桩基码头结构的弹性模量较大,且各部分连接牢固,有限元分析中对其建立整体弹性模型,土体采用ABAQUS有限元软件的Mohr-Coulumb塑性模型。因主要研究结构长期稳定性,故采用总应力分析方法。
4.4 有限元分析结果
在极限状态下,地基土体塑性变形分布如图7所示,结构的应力场分布如图8所示。由图可知:1)地基土体塑性变形最大的位置在前桩底部附近;2)导管架及桩周围土体均出现较大塑性变形,并呈贯通趋势;3)桩的应力明显大于上部板格结构,前桩应力几乎分布于整个桩体,后桩应力主要分布于桩的上半部分。由此可见,板格形导管架桩基码头结构的稳定性主要取决于地基土体的承载能力,在极限状态下,结构以前桩作为支承发生转动失稳。

图7 极限状态下土体塑性变形最大值处Fig.7 The maximum plastic deformation of soil in the limit state
为便于分析,选取临海侧码头顶部与导管架空腔土体接触的结点作为分析特征点,即图6(b)的A点,绘制该点的土体强度折减系数—结构位移关系曲线(Fr-S曲线),如图9所示。考虑到强度折减法的基本思想与传统的极限平衡法一致,均可称之为强度储备安全系数法。因此,结合极限承载力判别标准,以Fr-S关系曲线斜率接近于零时对应的折减系数作为结构稳定性安全系数。此时,土体抗剪强度指标几乎不再变化,抗倾作用力达到极限,结构发生失稳破坏。根据该判别准则,码头结构稳定性安全系数为1.46。

图8 极限状态下结构应力场分布云图Fig.8 Stress field of structure in the limit state

图9 Fr-S关系曲线Fig.9 Fr-S curves
4.5 简化方法与有限元结果比较
通过简化方法和有限元法对板格形导管架桩基码头稳定性进行分析,通过两种方法求得的不同结构尺寸的稳定性安全系数如表3所示。结果表明:选取不同结构尺寸,根据板格形导管架桩基码头稳定性简化计算方法确定的稳定性安全系数与对应的有限元结果相差较小,两种方法的计算结果较为吻合。

表3 有限元与简化方法折减系数对比Tab.3 Comparison of reduction factor Fr by FEM and simplified method
5 结语
板格形导管架桩基码头是适用于软土地基的新型码头结构型式,这里针对该码头结构的稳定特性进行了研究。
1)假定板格形导管架桩基码头结构发生倾覆失稳时,转动点位于前桩轴线上,且距导管架底面距离为L,对结构进行极限状态受力分析,基于假定转动点建立抗倾稳定性简化分析模型。将强度折减法应用于码头结构稳定性分析,根据其原理对结构作用力进行计算,建立平衡方程,求取稳定性安全系数。
2)选取天津滨海沿岸的水文及土层参数,利用ABAQUS三维弹塑性有限元分析软件建立该码头结构稳定性分析的数值模型。通过有限元模型,分析了结构的承载特性及破坏模式,明确了结构稳定性取决于地基的承载能力,且极限状态下结构以前桩为支承发生倾覆失稳,这与简化计算方法关于转动点位置的假定较为符合。根据折减系数随位移变化曲线,得到了土体作用力达到极限时(即曲线渐近线斜率接近于零)结构的稳定性安全系数。
3)将简化方法得到的稳定性安全系数与有限元结果进行比较。结果表明,两种方法计算结果较为吻合。
[1] 王元战,王海龙,付瑞清.沉入式大直径圆筒码头稳定性计算方法研究[J].岩土工程学报,2002,24(4):417-420.
[2] 王元战,华蕾娜,祝振宇.软土地基条件下大型圆筒海岸结构稳定性计算方法[J].岩土力学,2005,26(1):41-45.
[3] 肖 忠,王元战,及春宁,等.波浪作用下加固软基上大圆筒结构稳定性分析[J].岩土力学,2010,31(8):2648-2654.
[4] 肖 忠.软土地基上新型防波堤结构的稳定性分析[D].天津:天津大学,2009.
[5] 文靖斐,徐少鲲,别社安.箱筒型基础承载力研究[J].水运工程,2011,454(6):136-142.
[6] 伍晓峰,刘祚秋.格形钢板桩抗倾覆稳定性计算新方法[J].水运工程,2011,461(12):46-49.
[7] 王元战,王举睿.格形钢板桩结构稳定性的有限元数值分析[J].港工技术,2012,49(2):31-34.
[8] American Petroleum Institute(API).Recommended Practice for Planning,Designing and Constructing Fixed Offshore Platforms[S].American Petroleum Institute Publishing Services,Washington D C,2000.
[9] JTS167-2-2009,重力式码头设计与施工规范[S].北京:人民交通出版社,2009.
[10]JTJ215-98,港口工程荷载规范[S].北京:人民交通出版社,1998.
[11]史佩栋.实用桩基工程手册[M].北京:中国建筑工业出版社,1999.
[12]李春忠,陈兴国,樊有维.基于ABAQUS的强度折减有限元法边坡稳定性分析[J].防震减灾工程学报,2006,26(2):207-211.
[13]郑鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003(1):21-27.
[14]谭晓慧,王建国,刘新荣,等.边坡稳定的有限元可靠度计算及敏感性分析[J].岩土力学与工程学报,2007,26(1):116-121.
