基于Kriging 模型的车门刚度和模态优化

朱茂桃，钱 洋，顾娅欣，周泽磊，刘雪莱

(江苏大学汽车与交通工程学院，镇江 212013)

前言

车门是轿车的重要组成部分，应满足刚度、强度和模态性能的要求。同时，车门轻量化是改善车辆燃油经济性的重要措施之一［1］。因此对车门结构进行多目标多学科的优化显得十分重要。

为提高计算效率，灵敏度分析方法得到了广泛应用，其目的是以灵敏度分析为依据确定优化模型的设计变量。随着近似模型的广泛应用，近似模型的建模方法已从传统试验设计方法和响应面法逐渐转为选用现代试验设计方法和复杂近似拟合方法，目的是为了获得预测精度较高的模型［2-3］。

本文中根据某车门刚度和模态分析结果，对车门各钣件厚度进行灵敏度分析，将影响车门刚度和模态性能的关键钣件作为设计变量，进行拉丁方试验设计，利用Kriging模拟技术构建近似模型，选用序列二次规划法进行尺寸优化，从而在提高车门刚度和模态性能的同时，实现车门的轻量化。

1 车门刚度和模态有限元分析

车门主要是由厚度不足2mm的薄板冲压焊接形成，其长度和/或宽度方向的尺寸远大于厚度方向的尺寸，符合壳单元的理论假设，如图1所示。因此主要采用壳单元进行离散化［4］，网格大小为10mm，并对单元参数进行控制。焊点采用rigid刚性单元模拟。整个车门统一采用08AL材料，弹性模量为207GPa，泊松比为0.3，密度为7 800kg/m3。

建立的车门有限元模型包含26 300个节点、25 546个单元，其中有24 447个四边形单元，633个三角形单元，466个刚性单元，如图2所示。

通过Optistruct求解器，分别对车门的下沉刚度、扭转刚度、外板静压刚度和模态性能进行有限元分析，其结果如图3所示。车门的右上角扭转刚度明显不足，变形达13.2mm，大于某企业的评价标准10mm。车门1阶模态振型如图4所示，表现为外板上部窗框处弯曲，窗框下边沿弯曲变形最大。车门1阶模态频率值为34.83Hz，与一般情况下轿车车身1阶固有频率相近，存在共振的可能性，故须进行扭转刚度和模态性能的优化，即在满足车门扭转刚度和模态性能要求的前提下，以车门质量最轻为目标进行结构优化［5］。

2 车门模态试验

为验证车门有限元模型的正确性，对车门进行模态试验，并将车门的试验模态与理论模态进行对比分析。试验模态采用固定单点锤击，逐点拾取响应信号。采用充气内胎支撑模拟自由-自由边界［6］，测点布置采用100mm×100mm间距，共有109个测点。测试系统组成如图5所示。

激励信号与响应信号经过ICP放大器输入到SD380动态信号分析仪，经过FFT分析得到激励点与响应点之间的频率响应传递函数。在Star分析软件中利用多项式拟合法对所有频响函数进行曲线拟合，通过模态参数识别，得到车门模态参数。

试验模态分析结果与模态仿真结果的对比如表1所示。

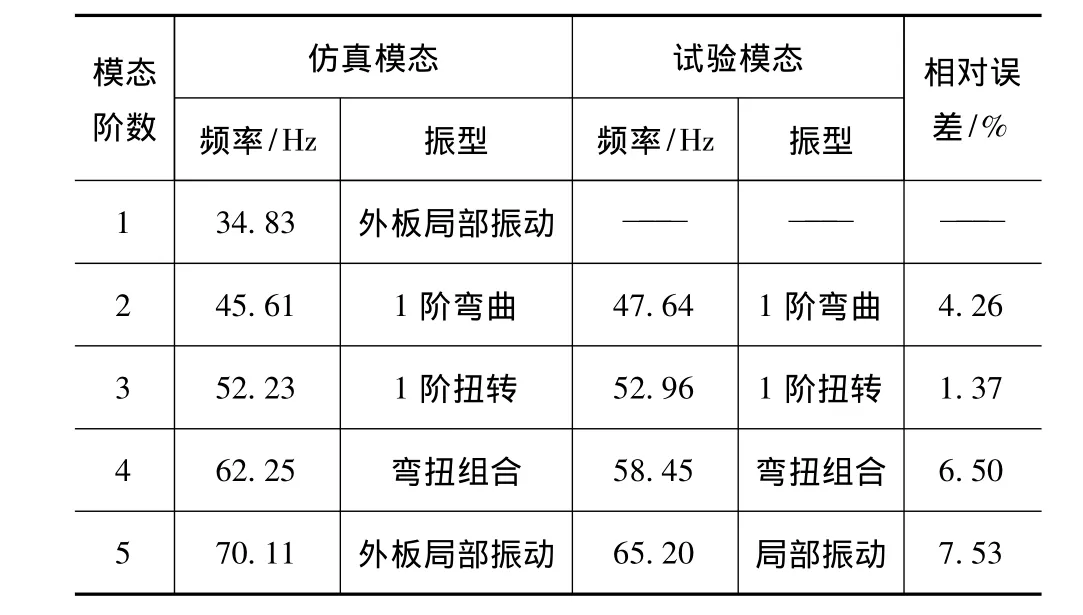
表1 车门仿真模态与试验模态结果对比

由表1可知，前5阶模态中，试验模态比仿真模态要少1阶频率，总体来看是由于仿真模态分析中所搭建的模型节点数要远远超过试验模态中的测点数，从而导致一些仿真模态在试验中没有出现。总体而言，相对应的仿真模态和试验模态频率值、振型较为一致。第5阶模态频率相对误差值最大，达到7.53%，但仍满足小于10%的误差要求。这主要是由于有限元模型的简化、焊点位置模拟不准确以及试验中不可避免的误差所造成的。

综上所述，车门仿真模态与试验模态分析的频率相近、振型相似，因此该有限元模型有效地反映了车门实体属性。建立的车门有限元模型能进一步进行灵敏度分析和性能优化。

3 车门各钣件灵敏度分析

在进行结构优化之前，通过灵敏度分析可以确定结构响应对各个钣件厚度的敏感程度，找到关键钣件作为车门性能优化的设计变量，以提高优化效率。以车门8个钣件厚度为设计变量，在Optistruct求解器中计算车门质量、1阶固有频率和扭转刚度对各个设计变量的灵敏度，此处扭转刚度用扭转工况下的最大变形来度量。计算结果如表2所示。其中，T1～T8分别代表内板、外板、内板加强板、外板加强板、门锁加强板、门锁支承加强板、铰链支承加强板和防撞梁的厚度。

表2 车门钣件灵敏度分析值

基于本文的优化目标和约束，为了考虑车门扭转刚度和1阶固有频率的提高对车门总质量的影响，定义扭转刚度相对灵敏度和1阶频率相对灵敏度［7］分别为

式中:M为车门质量对钣件厚度的灵敏度;D为最大变形对钣件厚度的灵敏度，该值为负表示随着钣厚增加，最大变形降低，相应的扭转刚度提高，因此-D则相当于扭转刚度对钣件厚度的灵敏度;F为车门1阶固有频率对钣件厚度的灵敏度;μDM为扭转刚度和质量对钣件厚度的相对灵敏度;μFM为1阶固有频率和质量对钣件厚度的相对灵敏度。当μDM(或μFM)为负时，表明减小钣厚时，质量减少，对应的扭转刚度或1阶频率反而增加，这是最理想的情况，对应的钣件厚度应选为设计变量，当然在实际情况中，这种情况出现的几率不太多;当μDM(或μFM)为正时，表明随着钣件厚度的增加，质量和扭转刚度同时增加，这虽然不是最理想的情况，但是可在提高扭转刚度的同时，尽量减少质量的增加，这就要看μDM值的大小，其值越大，说明在增加相同质量时，其扭转刚度提高得越多，即该钣件厚度变化对扭转刚度的影响远大于对质量的影响。在这种情况下，应选择μDM值较大的钣件厚度作为设计变量;当 μDM(或μFM)值趋近于零时，表明扭转刚度或1阶固有频率对该钣件厚度的灵敏度远小于质量对该钣件厚度的灵敏度，因此，在以增加刚度和频率、减小质量为目标的优化中，尽量不选择这些钣件厚度为设计变量。其它情况可同理类推。

由表2可见，钣件 T1～T4的 μFM和 μDM值皆为正，且数值都比T7、T8大，故可选为优化的设计变量;T5为负值(尽管数值不大)，也可选为设计变量。因此，最终选择内板(T1)、外板(T2)、内板加强板(T3)、外板加强板(T4)和门锁加强板(T5)作为优化的设计变量。

4 车门性能优化流程

依据所选定的5个钣件厚度作为优化的设计变量，建立的优化数学模型为

设计变量:T1～T5

式中:m为图3中8个钣件的质量总和，车门优化的目标是质量最轻;d为扭转工况下变形最大的41 800号节点的位移;f为车门1阶固有频率;T1～T5为5个钣件的原始厚度，Timin为各设计变量的下限值，Timax为各设计变量的上限值。

4.1 拉丁方试验设计

建立高精度的近似模型很大程度上取决于对设计空间的采样技术。用合理的试验设计方法均匀分布样本点，可有效地保证近似模型的精度。拉丁方试验设计是一种基于随机抽样的试验设计方法，具有均衡分散性和整齐可比性等特点，适用于多因素、采样空间大的研究［4］。

在Hyperstudy软件中，设定上述5个设计变量，以及质量、位移和频率3个不同类型的响应。应用拉丁方试验设计进行5因素100水平的试验设计，则可对因素的每个水平都进行一次试验，从而获得100组因素与响应对应关系的样本数据。

4.2 Kriging模型的拟合

Kriging技术是一种半参数化的插值技术，其作用是通过部分已知的信息去模拟某一点的未知信息。相对于传统的模拟技术而言，Kriging模型无须建立一个确定的数学模型，因此使用更为方便、灵活。Kriging近似技术更具有“统计性”，其有效程度不受已知信息中包含的噪声信息的影响［8］。因此，采用Kriging近似模型能得到更高的精度。

文中采用Kriging方法建立车门质量、扭转刚度和1阶频率的近似响应面模型。近似模型的精确程度对于优化结果的可信性至关重要［9］。采用均方根误差来描述近似模型拟合过程中产生的误差，以检验近似模型的精确性。表3列出了质量模型、扭转刚度模型和1阶频率模型的预测误差。

表3 Kriging近似模型均方根误差

由表3可知用Kriging方法构建的近似模型的误差都远小于0.01%，具有较高的精度，因此可用该Kriging近似模型代替有限元模型进行优化。

4.3 序列二次规划法优化与结果分析

以车门在扭转工况下右上角41 800号节点处的变形不超过10mm和车门1阶固有频率不小于38Hz作为约束。以车门质量最轻作为优化目标。综合考虑优化的精度、计算规模和普适性，选择序列二次规划法作为优化方法。优化在进行了16次迭代后结束。车门质量、扭转变形和1阶频率响应的收敛过程分别如图6～图8所示。

由图6可知，目标函数质量在第3次迭代点的计算值明显小于在第2次迭代点的计算值。由图7可知，明显满足位移约束d≤10mm的有第2次迭代点和第3次迭代点。而由图8可知，第2次迭代点和第3次迭代点都满足频率约束f≥38Hz，且第3次迭代点的计算值明显高于第2次迭代点的计算值。综上所述，第3次迭代点为最优解。关键钣件厚度的具体取值范围、响应的初始值和近似模型的优化值如表4所示。

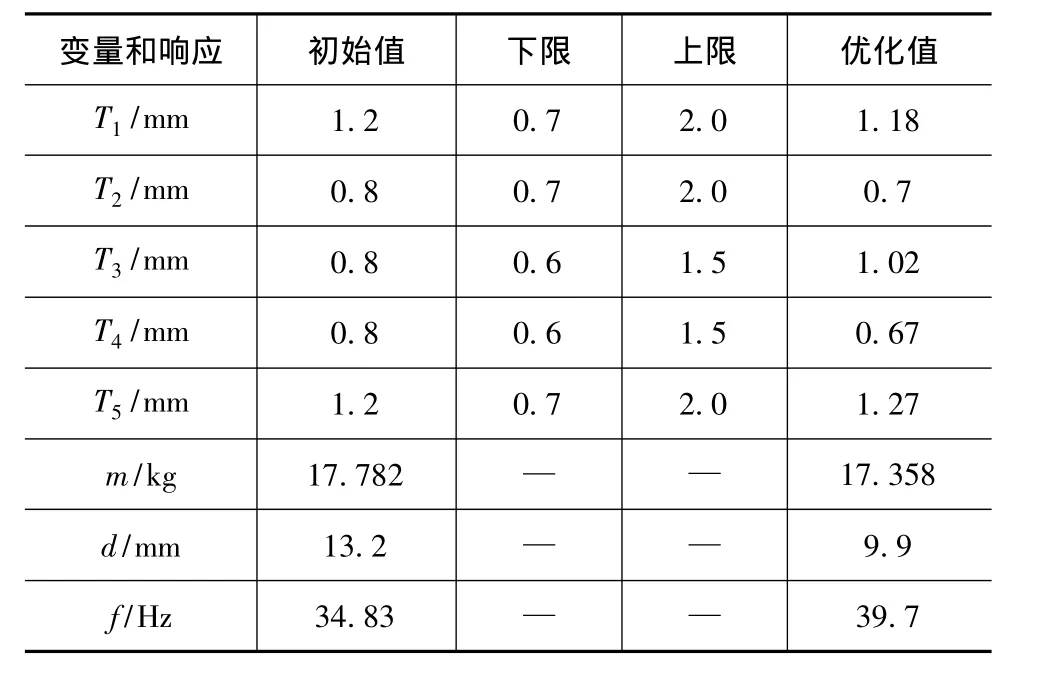
表4 变量与响应的初始值、上下限和优化值

为验证基于Kriging近似模型优化结果的精确性，须对模型预测的最优值与有限元模型仿真值进行对比分析［9］。将各钣件厚度最优值代入原有限元模型进行仿真计算，结果表明基于Kriging模型的车门性能优化结果具有一定的可靠性。优化后的车门不仅满足所有的设计约束，而且车门质量减轻了2.38%，车门1阶固有频率提高到39.7Hz，有效降低了与车身低阶模态发生耦合共振的可能性。

5 结论

采用灵敏度分析方法准确地找到影响车门扭转刚度和模态性能的关键钣件，并将其作为设计变量。结合拉丁方试验设计法、Kriging模拟技术和序列二次规划算法，在保证车门轻量化的同时实现了改善车门的扭转刚度和模态性能的目标。将灵敏度分析方法与基于Kriging近似模型的优化相结合，既提高了优化效率，又保证了计算精度。

［1］ 易辉成.基于刚度和模态的车门结构件料厚多目标优化设计研究［D］.长沙:湖南大学，2011.

［2］ 曹文钢，曲令晋，白迎春.基于灵敏度分析的客车车身质量优化研究［J］.汽车工程，2009，31(3):278-281.

［3］ Song S I，Park G J.Multidisciplinary Optimization of an Automotive Door with a Tailored Blank［J］.Automobile Engineering，2006(2):151-163.

［4］ 王国春，成艾国，胡成辉，等.基于Kriging模型的汽车前部结构的耐撞性优化［J］.汽车工程，2011，33(3):208-212.

［5］ Kodivalam S，Yang R J.Multidisciplinary Design Optimization of a Vehicle System in a Scalable High Performance Computing Environment［J］.Structural and Multidisciplinary Optimization，2004，26:256-263.

［6］ 黄石华.基于刚度特性的车身结构轻量化研究［D］.长沙:湖南大学，2011.

［7］ 郝琪，张继伟.车门结构优化设计的灵敏度分析研究［J］.汽车技术，2010(5):40-44.

［8］ Hao Qi，Sun Yuan.Car Door Optimization Based on Kriging Model［M］.New York:ACM Press，2010:23-26.

［9］ 邳薇，崔新涛，王树新.基于Kriging模型的汽车车门抗撞性优化设计［J］.组合机床与自动化加工技术，2007(1):29-31.