地板辐射采暖系统温度分布测试及数值分析
2013-10-10孟庆龙章立新
赵 明, 孟庆龙, 杨 茉, 章立新
(1上海理工大学 能源与动力工程学院,上海 200093;2张家港迪爱生化工有限公司 技术开发部,张家港 215635)
低温地板辐射采暖是一种以辐射换热和自然对流换热相结合的形式对室内进行供暖的方式,与传统的采暖方式相比具有热舒适性好、节省空间及节能环保等优点.目前市场上地面辐射采暖主要有两种方式:一是低温热水采暖,二是电采暖(发热电缆或电热膜).随着管材材料工艺水平的提升,低温热水地板辐射采暖成为国家大力提倡的一种新型采暖方式,近年来特别在我国北部地区得到迅速发展.
关于低温热水地板辐射采暖的设计计算及流动和传热的特性方面,国内外已有大量的报导.如Anderson[1]计算了地板层空间的传热量.Bánhidi等[2]研究了不同采暖方式下,人体模型的散热特点,结果发现辐射采暖方式包括地板辐射采暖较传统的加热方式有更好的热舒适性.Weitzmann等[3-4]分别采用5种不同模型详细研究了各种技术参数下地板层的散热量及不同模型所对应的地板表面温度,其中包括低温热水地板辐射模型和电加热地板辐射模型.Olesen[5-6]较早开展了一系列的研究,并在文献[7]中报导了通过实验研究使用普通散热器和低温热水地板辐射采暖的区别,结果发现采用两者取暖方式的室温都可容易地得到控制.Olesen[8]在随后发表的一篇综述文章中,详细介绍了地板辐射采暖的一些技术特点,包括室温控制、地板表面温度的影响因素以及设计计算等.Sattari等[9]采用有限差分法系统研究了各种参数对低温热水地板辐射性能的影响,包括管径、水管的数量、水管的材料、地面覆盖物的材料和厚度等因素,结果显示地面覆盖物的材料类型和厚度是地板采暖设计中最重要的影响因素.
关于地板辐射采暖系统的数值模拟和实验方面,国内外的研究者也作了大量的研究.Chapman等[10]用实验和数值模拟相结合的方法进行地板辐射采暖中地表加热量的研究,得出了一些指导性的结论,但因为影响地表热流量的因素很多,无法给出一个简单确定地实验关联式直接进行计算.侯书新[11]就安装低温热水地板辐射采暖装置的某宾馆房间进行室温的实地测试,并与传统散热器供暖方式的室温作对比.马良栋等[12]通过抽象出的二维、稳态、湍流模型进行数值分析,地板表面取为均匀热流,顶棚和内墙表面视为绝热,数值结果从理论上说明了地板辐射采暖热舒适性的原因.陈占秀等[13]对地板辐射采暖房间建立三维、稳态的湍流模型,进行数值求解.所用湍流模型为κ-ε模型,具体计算时,首先计算出辐射换热量,然后将之视为常热量边界加到对流换热模型中,每个表面均为第二类边界条件.刘翔等[14]利用实验分析了影响低温热水地板辐射供暖系统达到稳态运行的热工性能,并在此基础上,建立了传热过程的数学模型,确定了管间距、供回水平均温度、地板表面覆盖层等因素影响地暖达到稳态的关系,指出了除表面覆盖层对其影响较大以外,其余因素相对较小.刘巧焕等[15]叙述了地板辐射采暖系统工程设计的计算方法,并进行了简单的数值计算.孙德兴等[16]主要对地暖施工中的技术问题进行了详细探讨.
综上所述,在相关的数值计算所用湍流模型中,研究者们全部直接采用的是κ-ε湍流模型进行计算,实际上在对不同的物理模型进行三维湍流流动的数值计算时,不同湍流模型的选择对数值结果的影响还存在分歧[17-18].本文首先介绍加装低温热水地板辐射采暖房间的温度分布的实验测定结果;其次利用商用CFD软件Fluent进行地板辐射采暖房间内的三维流动与换热的数值模拟,主要考核4种不同的湍流模型:一方程的Spalart-Allmaras模型、两方程的标准κε模型、κ-ε旋流修正模型和重正化群(Renormalization-group,RNG)κ-ε模型,对数值结果的影响,并在与实验数据相比较的基础上,探讨不同湍流模型对所研究问题的适应性.
1 低温热水地板辐射采暖房间的温度分布测定
1.1 实验系统
实验的目的主要是通过实验的手段获得低温热水地板辐射采暖房间的温度分布特性,在此基础上可进一步评价该取暖方式的热舒适性等指标,并为后续的数值计算提供比较依据.
待测的低温热水地板辐射采暖房间采用壁挂式燃气锅炉加热循环热水,水管的排列方式为单蛇形.供暖区域中待测房间如图1(a)(见下页)所示,房间有两面墙为内墙,两面墙为外墙,外墙中的一面墙有3扇双层玻璃的窗户.房间长、宽、高分别为:473,333和265cm.图1(a)中给出了测点25的位置.房间内整个空间划分为5层,高度依次为距离地面44,88,133,171和221cm,每层共放置30个测点,各测点的位置如图1(b)(见下页)所示.
实验开始时,采用壁挂式锅炉加热热水的地板辐射采暖系统已运行超过24h,房间内温度已达到稳定.供水温度60℃,回水温度25℃.实验材料包括:30个已经制作好的并经过标定的热电偶、数据采集仪、冰瓶、卡尺、线团和胶带等.
实验步骤如下:
a.对房间的几何尺寸进行测量,获得房间的几何参数.
b.根据房间的几何参数布置热电偶,如图1(b)所示,将房间的内部空间分5层来测量.
c.将热电偶连接至数据采集仪,进行调试.
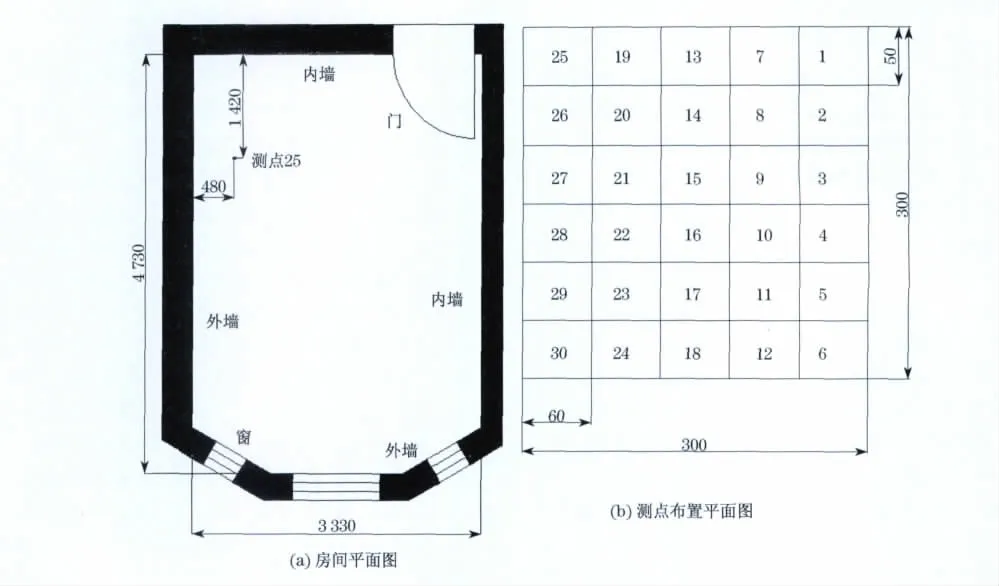
图1 房间和测点布置平面图Fig.1 Room and the measuring point layout
d.首先闭门测量,等待数分种,直至房间内部达到稳定状态之后,读取各热电偶的数据,隔5min之后再读一次,每个工况读3组数据.
e.开门测量,隔5min读取2组数据.
f.改变热电偶的位置,将热电偶放置于另一层进行测量(测量顺序依次为距离地面高度221,171,133,88和44cm),重复操作第d步和第e步.
g.记录所有的数据.
1.2 实验结果及分析
分别针对房间封闭时(即关门)和开门时进行测定.其中关门时所测得的其每一层的30个测点温度最大值tmax、最小值tmin和两者差值Δt及每一层的温度平均值t—列于表1中.z为距离地面的高度.
由表1可知,z为0时,所测地表温度的最大值和最小值相差较大,原因是最小值的测点正好放置于靠近墙壁的位置,而这个位置已位于所埋设热水管的外面,所以相应测得的温度偏低,而最大值的测点正好放置于所埋设热水管的正上方,所以相应测得的温度偏高,而测点布置在所埋设热水管中间位置的,相应测得的温度位于中间值.从所测数据的统计数据看,地表温度的分布是不均匀的,波动幅度在3℃左右.表1同样示出,房间的空间温度分布即z为44,88,133,171和221cm 时,均匀性较好,特别是z为44,88和133cm时,最大值和最小值的差别都小于2℃.在44cm≤z≤171cm的高度范围内,温度竖向分布也差别不大,其每层平均值的最大差别仅为0.73℃,而这些高度区域,正好处于人活动的空间,所以热舒适性会较好.
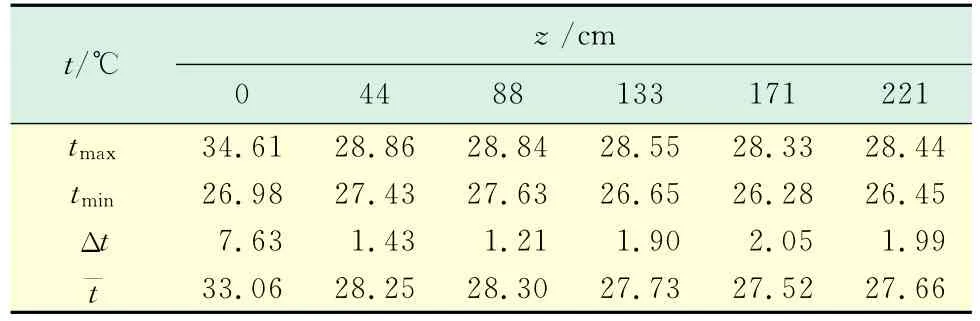
表1 测点的温度分布统计Tab.1 Temperature distribution statistical results for all measuring points
图2示出了整个房间内的温度分布,地板表面温度明显高于空间温度,z为44,88cm时的空间温度普遍高于z为133,171和221cm时的温度,即地板辐射采暖房间内温度分布总体上是自下而上,温度从高到低变化,但空间的温度变化幅度不大.
为了探明当房间不封闭时,即开门时对房间内温度的影响(开门后等待房间温度稳定后开始测定,该门为内门,门外环境温度为27℃),房间开门时的温度分布也被测定,并和闭门时相比较,结果如图3所示.
由图3可知,当地板辐射采暖房间开门时,空间内每一层的温度分布(即z为44,88,133,171和221cm)也比较均匀,但地表温度(即z为0)的均匀性较差.开门处的气流对温度分布的均匀性基本没有影响,但受此气流影响,开门时各个测点的温度和闭门时相比较普遍降低,但地板表面温度还维持原来水平.
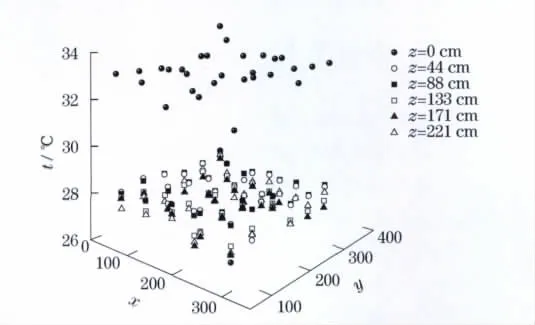
图2 整个房间内的温度分布Fig.2 Temperature distribution of the room
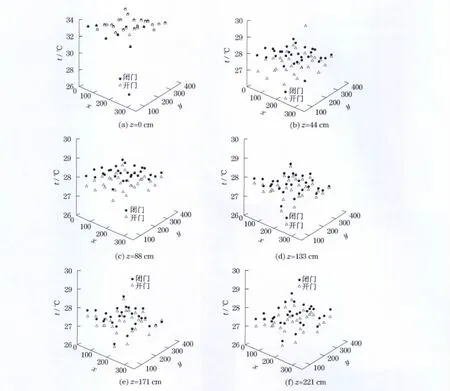
图3 各层的开门和闭门时的温度分布Fig.3 Temperature distrbution of the room while door is opened or closed
2 湍流模型的考核
2.1 物理模型和数学模型
所抽象出的加装地暖设备房间的物理模型示意图如图4所示,房间的长、宽、高分别为473,333和265cm,壁面1为加热面,壁面4和5为外墙,其余均为内墙.为简化计算,模型不设窗户,皆视为壁面.数学模型中的对流模型基于如下假设:假设图4所示空间内流体为Boussinesq型流体;流动和换热为自然对流和辐射耦合的三维稳态湍流.辐射模型为Fluent中的S2S模型,该模型主要用来计算介质不参与辐射,仅固体壁面之间特别是封闭区域内的各不同表面间的辐射换热.所研究房间的各壁面发射率除底面取为0.7外,其余壁面均取值为0.8.近壁面处理采用标准壁面函数法,网格均分为50×50×50.
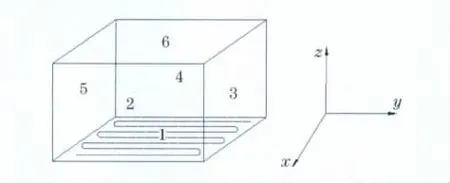
图4 物理模型示意图Fig.4 Physical model
边界条件:除房间的地板表面1外,房间的其余壁面均采用第一类边界条件,温度数值为实验测得值,地板表面采用第二类边界条件.当地板表面同时存在辐射和对流换热时,在实际的地暖设计计算中常采用文献[18]中的经验公式来计算地板表面散热量,本文同样采用文献[18]中的经验公式,计算地板表面的辐射换热量和对流换热量,并将两者之和作为边界总的热流值,计算得q=57.57W/m2.
2.2 不同湍流模型的计算结果
a.Spalart-Allmaras一方程模型
采用一方程的Spalart-Allmaras模型时的计算结果同图2所示的实验数据相比较如图5所示.
由图5示出的一方程的Spalart-Allmaras模型计算结果和实验数据相比可知,其计算出的温度数值和实测值相比,总体偏大,存在的误差最大为9%.
b.标准κ-ε、RNGκ-ε和κ-ε旋流修正两方程模型的比较
采用3种两方程模型即标准κ-ε模型、RNGκ-ε模型和κ-ε旋流修正模型分别进行计算,数值计算结果和实验数据中所取的两个参考点即z为88和221cm时所测得的平均温度相比较的结果如表2所示.
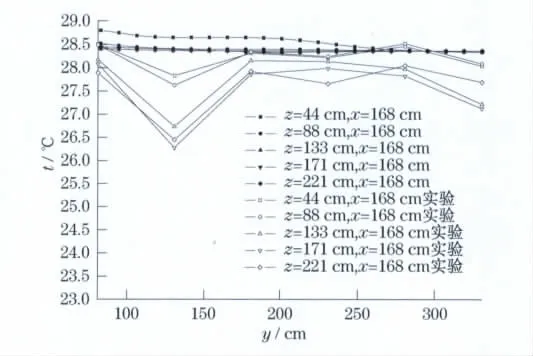
图5 Spalart-Allmaras模型数值结果和实验数据的比较Fig.5 Comparison between numerical and experimental results for Spalart-Allmaras tubulent model
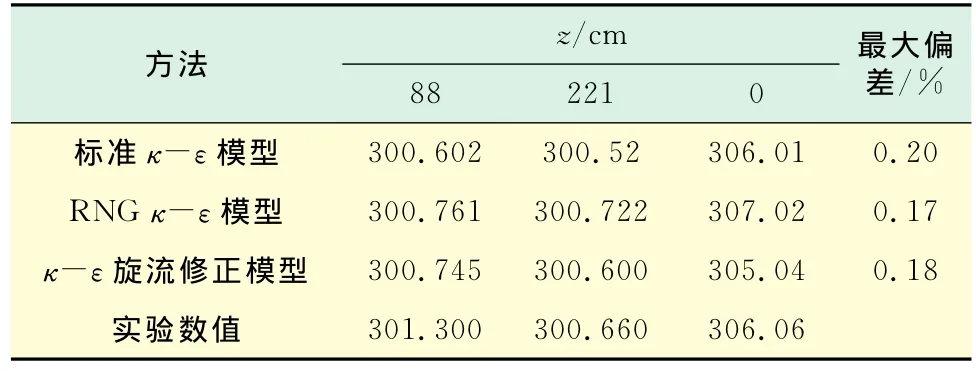
表2 3种两方程模型的比较Tab.2 Comparison of three two-equation turbulent models K
由表2可看出,3种模型的模拟结果皆和实验数据接近,其温度场也符合实验所测定的温度分布特性,图6和图7仅列出采用标准κ-ε模型计算时的流场和温度场,图中温度的单位为K,速度的单位为m/s,截面位置单位为cm,其同实验数据详细比较如图8所示.
由图6和图7可知,房间内温度分布的总体特点是非常均匀,各个截面上的温度梯度很小.整个房间内的流场呈环形,近壁面处存在较大流速,主流区域的流速很小.和实验数据相比(如图8所示),数值计算结果围绕实验结果小幅波动,最大偏差不到1%.由此可知,所用标准κ-ε模型的数值计算结果和实验数据吻合得较好,给出了房间内较接近实测数据的温度数值和均匀的温度场分布特性.就最大偏差而言,由表2可看出,3种方程的偏差基本近似相等,差别不大,但标准κ-ε模型所需计算时间及占用CPU更少,所以从精度和所需计算时间的经济性等角度综合考量,标准κ-ε模型已能满足数值计算要求,低温热水地板辐射采暖的数值模拟工作,均可采用标准κ-ε模型进行计算.
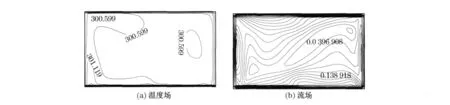
图6 x=166.5cm截面的温度场和流场Fig.6 Streamline plot and temperature contour at x=166.5cm
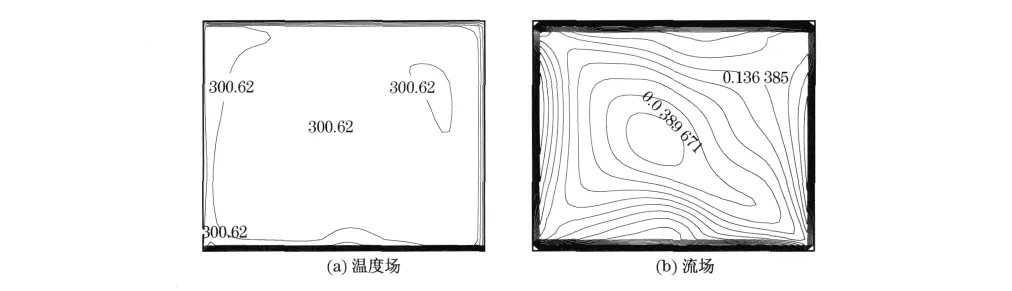
图7 y=236.5cm截面的温度场和流场Fig.7 Streamline plot and temperature contour at y=236.5cm
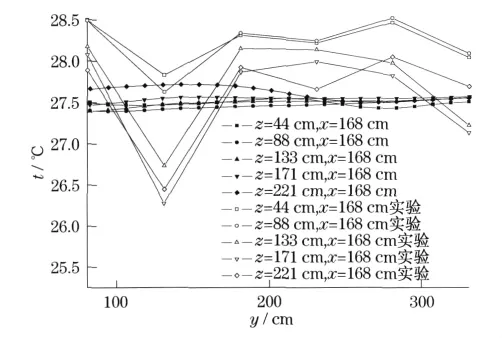
图8 标准κ-ε模型数值结果和实验数据的比较Fig.8 Comparison between numerical and experimental results for standardκ-εturbulent model
3 结 论
a.实验结果表明,地板辐射采暖房间内温度分布总体上是自下而上,温度从高到低变化,地板表面温度最高,但空间的温度变化幅度不大;而且处于人活动的空间范围中,温度竖向分布差别不大,具有良好的热舒适性.此外,房间开门或闭门,空间内每一层的温度分布都比较均匀.开门处的气流对温度分布的均匀性基本没有影响,但受此气流影响,开门时各个测点的温度和闭门时相比较普遍降低,但地板表面温度还维持原来水平.
b.从精度和经济性等角度考量,标准k-ε模型已能满足数值计算要求,数值计算结果很好地模拟出了地板辐射采暖房间的温度分布特性,并和实验数据相比吻合得也较好.
[1]Anderson B R.Calculation of the steady-state heat transfer through a slab-on-ground floor[J].Building and Environment,1991,26(4):405-415.
[2]Bánhidi L,Somogyi A,FabòL,et al.Compensation of asymmetric radiant heat loss to cold walls by different heating systems-analysis with thermal manikin[J].Environment International,1991,17(4):211-215.
[3]Weitzmann P,Kragh J,Jensen C F.Numerical investigation of floor heating systems in low energy houses[C]∥Proceedings of the Sixth Symposium on Building Physics in the Nordic Countries,Trondheim:2002,905-912.
[4]Weitzmann P,Kragh J,Roots P,et al.Modelling floor heating systems using a validated two-dimensional ground coupled numerical model[J].Buildings and Environment,2005,40(2):153-163.
[5]Olesen B W.A simplified calculation method for checking the indoor climate[J].ASHRAE Transactions,1983,98(2B):710-723.
[6]Olesen B W.Thermal comfort in a room heated by different methods[J].ASHRAE Transactions,1980,86(1):34-48.
[7]Olesen B W.CoMParative experimental study of performance of radiant floor heating system under dynamic conditions[J].ASHRAE Transactions,1994,100(1):1011-1023.
[8]Olesen B W.Radiant floor heating in theory and practice[J].ASHRAE Journal,2002,7:19-24.
[9]Sattari S,Farhanieh B.A parametric study on radiant floor heating system performance[J].Building and Environment,2007,42(3):1043-1053.
[10]Chapman K S, Shultz J D. Develop simplified methodology to determine heat transfer design impacts associated with common installation alternatives for radiant conduit[R].ASHRAE final report,RP-1036,Manhattan:National Gas Machinery Laboratory,Kansas State University,2002,1-44.
[11]侯书新.低温热水地板辐射供暖的室内温度竖向分布的测试与分析[J].北京建筑工程学院学报,2003,19(2):30-32.
[12]马良栋,陶文铨,戴颖,等.室内低温地板辐射采暖的温度分布及湍流流动数值模拟[J].工程热物理学报,2005,26(3):501-503.
[13]陈占秀,赵虎城.地板辐射采暖房间三维流动与传热的数值模拟[J].河北工业大学学报,2006,35(4):49-52.
[14]刘翔,王长庆,黄奕沄,等.华东地区低温地板辐射采暖实验及模拟[J].能源技术,2007,28(1):40-44.
[15]刘巧焕,孙志宝,张连钢,等.热水地板辐射供暖系统的设计与数值模拟[J].煤气与热力,2007,27(2):83-85.
[16]孙德兴,陈海波,张吉礼.低温热水供暖技术推广中尚需研究解决的问题[J].暖通空调,2002,32(3):99-102.
[17]Kuznik F,Rusaouen G,Brau J.Experimental and numerical study of a full scale ventilated enclosure:Comparison of four two equations closure turbulence models[J].Building and Environment,2007,42(3):1043-1053.
[18]Bartzanas T,Kittas C,Sapounas A A,et al.Analysis of airflow through experimental rural buildings:sensitivity to turbulence models[J].Biosystems Engineering,2007,97(2):229-239.
[19]陆耀庆.供热通风设计手册[M].北京:中国建筑工业出版社,1987.
