圆内开缝圆不同开缝方向自然对流换热

申春赟， 杨 茉， 王 津， 张 昆， 张玉文

（1.上海理工大学 能源与动力工程学院，上海 200093；2.密苏里大学 机械与航空航天工程学院，哥伦比亚 65211）

封闭圆内开缝圆自然对流换热是从发电厂采用的离相封闭电流母线散热问题中抽象出来的理论研究模型.由于封闭电流母线的热效应可能引起母线局部过热，从而导致母线短路等问题，会严重影响母线的正常安全运行，因此，必须对母线采取可靠而有效的散热措施.对于自然冷却的封闭电流母线，为了强化内筒电流母线自然对流换热，常常将内筒开缝，其抽象的换热模型即本文研究的封闭圆内开缝圆的自然对流换热问题.

最早研究圆内开缝圆自然对流换热的是Kuleek［1］，其首次提出了一个近似计算公式，说明了开缝结构下的换热量可以比不开缝结构下的换热量提高30%～40%.王国祥等［2］则对圆内开缝圆自然对流换热进行了实验研究，发现Kuleek的近似公式与实验结果之间存在较大的误差，并提出开缝结构下的换热量最大可以比不开缝结构下的换热量提高50%以上.Yang等［3］采用SIMPLE算法和稳态对称模型首次成功地对圆内开缝圆自然对流换热问题进行了数值模拟，所获得的数值结果与王国祥［2］的实验结果吻合.Yang、黄夫泉、Zhang等［4－6］对圆内开缝圆自然对流换热问题进行了更深入的研究，他们发现，对这种几何和物理条件都是对称的和不随时间变化的自然对流换热问题，由于问题是非线性的，除了存在稳态的和对称的解外，在满足一定条件时，还存在非对称的和振荡的解，对这种问题进行数值模拟需要采用完整的计算区域和非稳态模型.然而国际上的关于这方面的研究主要针对于封闭圆内自然对流换热，Bishop，Powe等［7－8］先后由实验研究了低温下两个同心圆筒所构成的环形封闭空间内氦气的自然对流换热，给出了Keqs与Ra的实验关联式.Farouk，Guceri和Saitoh等［9－11］均采用数值方法研究了这种环形空间内自然对流换热问题，Fant等［12－13］研究了二维狭小环形空间中的流动与换热问题，同时Yoo［14－15］研究了不同参数下狭小圆环内出现的非线性现象.但是如果对封闭圆进行开缝，其流场和温度场都会发生很大变化，因此，本文在前人研究基础上进一步对圆内开缝圆自然对流进行研究.

到目前为止，所见到的对于圆内开缝圆自然对流换热的研究，都是针对竖直开缝圆的.对于圆内水平开缝圆和开缝有一定角度的开缝圆自然对流换热，未见有公开发表出来的研究成果.由于自然对流换热受几何结构和几何位置的影响较大，特别是一些非线性特性对几何结构和几何位置变化较为敏感，因此，需要展开对各种开缝方向的圆内开缝圆自然对流换热的研究.

笔者采用非稳态的换热模型，对不同开缝方向的圆内开缝圆全区域的自然对流换热进行了数值模拟，根据数值结果，探讨了不同开缝方向及特征参数下对这种模型的换热规律及其中存在的非线性特性.

1 研究模型及计算方法

在极坐标下研究的理论模型如图1所示，假设其中的自然对流换热问题是二维的，其内外圆分别为恒温Ti和To，Ti＞To.φ为开缝圆开缝与竖直铅垂线所成的角度，φ＝90°时为水平开缝.当计算中所采用的半径比η＝ri／ro＝5／13、开缝度S＝2α／π＝0.1、环形空间宽度L＝1、内部圆环厚度δ＝0.112 5时，流体满足Boussinesq假设及流体在固壁上无滑移.

在极坐标系下，描述上述二维模型的无量纲化控制方程为

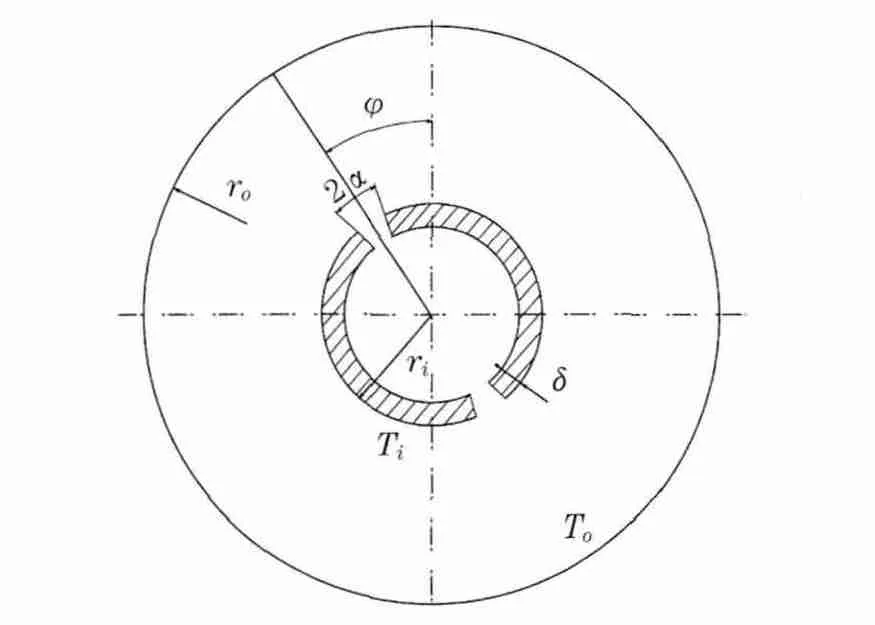
图1 封闭圆内开缝圆自然对流换热模型Fig.1 Closed circle within a slotted round natural convection heat transfer model

其中，方程（1）和方程（2）的源项分别为

方程中无量纲参数和参考值UR定义为

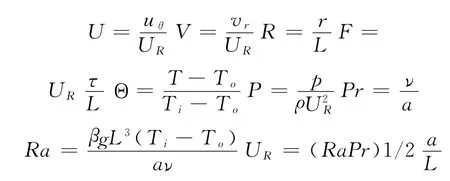
式中，ρ为流体密度；g为重力加速度；β为热膨胀系数；α为热扩散率；ν为运动粘度系数.

描述图1问题的边界条件为

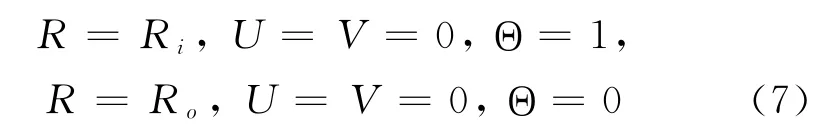
初始条件为

为了探讨不同Ra下整体的换热效果，定义整个圆的平均导热系数为

式中，Q为整个圆的换热量.

为了与文献［2］实验结果相对比，定义修正后的整体平均当量导热系数为

2 数值模拟及分析

2.1 模拟结果与王国祥实验结果对比

采用具有QUICK差分方法的SIMPLE方法对文献［2］实验所采用的封闭圆内竖直开缝圆模型进行计算.实验物理模型的几何尺寸为ro＝130，ri＝49，δ＝4.5，S＝0.1.实验所得关联式为

图2给出了具有QUICK差分方法的SIMPLE方法的数值与实验结果对比.由图可知，本文所构造的数值结果与实验结果吻合良好，能够有效地反映封闭圆内开缝圆的自然对流换热情况.当Ra较小时，两者几乎完全吻合，当Ra＝3×105时，两者的误差为6%.

2.2 不同开缝方向下流场和温度场的变化

图3（见下页）给出了Ra＝1×104时不同开缝方向下自然对流换热速度矢量场和温度场.与不开缝的结构相比，开缝圆的内部存在流体流动，内外两个表面均参与换热.流体沿开缝圆热壁面上升，至顶部开缝处后，沿外圆的冷壁面下降，最终形成两个较大涡卷.该流动结构下的流体在开缝圆正上方向上流动，这种流动称为上升流.该流场下对应温度条纹在开缝圆上方呈T字型，所以称为T字型温度场.从图中模拟结果可以看出，在环形区域的中上部出现了“肾状涡”，数值计算中在开缝圆内的下部出现了类似于“猫眼”的二次涡.

当φ＝10°时，温度分布不再沿着开缝方向而对称，对应的温度场在内部开缝圆上方区域呈现非对称的T字型，称为非对称T字型温度场.原来开缝圆内部较平直的等温线发生了偏斜.

当φ＝60°时，随着开缝方向的继续增加，高温区域逐渐开始收缩，不再呈现扩散的形式，高温区域开始向上运动，开缝环内的温度慢慢由低温区域变化为高温区域.

图2 二维数值与文献［2］实验结果对比Fig.2 Comparison of two－dimensional numerical and literature［2］experiment results

当φ＝90°时，流体沿开缝圆热壁面上升，一部分流体沿水平开缝处流入开缝圆内部，另一部分流体继续上升 到达开缝圆上方后 沿外圆筒冷壁面下降，圆内左右两侧形成了大小不同的两涡涡卷，该流型对应的温度场沿纵轴线不对称，在开缝圆上方呈现T字型，对应的T型温度场向右偏斜，称为非对称的两涡基本流型及T型温度场.

图3 不同开缝方向下对应的温度场和速度矢量场Fig.3 Temperature field and velocity field in different slotted direction

2.3 不同开缝方向Keqs的变化

图4所示为采用二维QUICK格式计算不同开缝方向Keqs的变化.

由图4（a）得知，当φ不变时，Keqs随着Ra的增加不断增大，而且不同开缝方向处Keqs随Ra的变化趋势一致.当Ra取10～102时，Keqs随着φ增大基本不发生变化，因为低Ra下对流与热传导相比，热传导占据主要地位，而开缝方向变化时热传导热量变化不大，因此Keqs基本不变.当Ra为102～105之间时，随着Ra的增加Keqs不断增大，相同Ra下φ越大Keqs越低.因为Ra的增加表明对流换热起到的作用越来越大，随着开缝方向的变化，由竖直偏斜慢慢变缓，由重力引起的自然对流换热逐渐减弱，导致Keqs降低.

图4 不同开缝方向时Keqs的变化Fig.4 Comparison of Keqsin different slotted directions

由图4（b）所示，当Ra不变时，随着φ的增大，Keqs逐渐减小.随着Ra继续增大，Keqs出现了波动，结果无法收敛，说明此时对流换热无法达到稳定，出现了振荡.

2.4 圆内开缝圆的非线性特性

当选择水平开缝圆几何尺寸为S＝0.4，Pr＝0.7，δ＝0.112 5时，采用SIMPLE方法计算不同Ra下自然对流换热问题.采用零初场，在几何尺寸不变时计算不同Ra下Keq随时间的变化，结果表明随着Ra不断增大，系统出现了不同的数值解，分别为稳态解、周期性振荡解及混沌解.当Ra＝105时，流动与换热处于稳定状态，Keq随时间趋于定值，如图5（a）（见下页）.当Ra＝106时，Keq随时间的发展不能够稳定于某一定值，经过足够长的时间后，随时间呈周期性振荡状态，如图5（b）（见下页）.当Ra＝107时，经过足够长的时间后，Keq随时间做非周期性振荡运动，流动与换热表现较强的非线性特性，如图5（c）（见下页）.

以上为水平开缝方向模拟的非线性现象，其它开缝方向也会出现类似的非线性特性，只是出现稳定解、周期性振荡解、非周期性振荡解的临界值有所不同，本文这里不再叙述.

图5 不同Ra下Keq随时间变化Fig.5 Keqchanges with time in different Ra

3 结 论

a.基于SIMPLE方法的计算结果能够与文献［2］的实验结果相吻合；

b.在本文模拟的水平开缝特定几何尺寸下，当Ra较小时，不同φ时Keqs基本保持不变，随着Ra增加，随着φ从竖直到水平角度变化时Keqs变小，而在同一开缝方向下Ra越大Keqs值越大，当Ra超过某一临界值时，Keqs出现波动，数值结果发生了振荡；

c.不同Ra下Keq随时间的变化，结果表明随着Ra不断增大，系统出现了不同的数值解，分别为稳态解、周期性振荡解及混沌解，圆内开缝圆自然对流换热表现出非线性现象.

［1］Kuleek P V.Heating and cooling of bus bars for large power generators［J］.Electric Power Plant，1964（10）：39－43.

［2］王国祥.双半圆大电流封闭母线自然对流换热实验研究［C］／／工程热物理论文集.北京.1986：235－240.

［3］Yang M，Tao W Q.A numerical study of nature convective heat transfer in an cylindrical enclosure with internal concentric slotted hollow cylinder［J］.Numerical Heat Transfer，1992，22（3）：289－306.

［4］Yang M，Zhang B W，Huang F Q，et al.Numerical simulation for nonlinear characters of natural convection in an annulus with an internal concentric slotted cylinder［C］／／13th International Heat Transfer Conference，Sydney Convention and Exhibition Centre，2006.

［5］黄夫泉，杨茉，余敏，等，封闭圆内开缝圆自然对流换热的振荡特性［J］.工程热物理学报，2006，27（2）：286－288.

［6］Zhang K，Yang M，Zhang Y W.Numerical analysis of natural convection in a cylindrical envelope with an internal concentric cylinder with slots［J］.Numerical Heat Transfer Part A，2011，59（10）：739－754.

［7］Bishop E H，Carley C T，Photographic studies of natural convection between concentric cylinders［C］／／Proceedings of the 1966Heat Transfer and Fluid Mechanics Institute.Stanford，1966.

［8］Powe R E，Bishop E H，Carley C T.Free convective flow patterns in cylindrical annuli［J］.Journal of Heat Transfer，1969，91（3）：310－314.

［9］Farouk B，Guceri S I.Natural convection from a horizontal cylinder－laminar regime［J］.Journal of Heat Transfer，1981，103（3）：522－527.

［10］Farouk B，Guceri S I.Laminar and turbulent natural convection in the annulus between horizontal concentric cylinders［J］.Journal of Heat Transfer，1982，104（4）：631－636.

［11］Saitoh T，Sajiki T，Maruhara K.Bench mark solutions to natural convection heat transfer problem around a horizontal circular cylinder［J］.International Journal of Heat and Mass Transfer，1993，36（5）：1251－1259.

［12］Fant D B， Prusa J， Rothmayer A. Unsteady multicellular natural convection in a narrow horizontal cylinderical annulus［J］.Journal of Heat Transfer，1990，112（2）：379－387.

［13］Fant D B，Rothmayer A，Prusa J.Natural convective flow instability between horizontal concentric cylinders［J］.Journal of Thermophysics，1991，5（3）：407－414.

［14］Yoo J S.Prandtl number effect on bifurcation and dual solutions in natural convection in a horizontal annulus［J］.International Journal of Heat and Mass Transfer，1999，42（17）：3279－3290.

［15］Yoo J S.Dual free－convective flows in a horizontal annulus with a constant heat flux wall ［J］.International Journal of Heat and Mass Transfer，2003，46（13）：2499－2503.