矩阵变换器的谐波注入PWM控制策略

王汝田，王秀云，崔永恒

（东北电力大学 电气工程学院，吉林 吉林 132012）

0 引言

自从1981年M Venturini证明了矩阵变换器的存在定理后[1]，矩阵变换器就以其优良的输入／输出性能，以及能量双向传递、无中间储能元件、结构紧凑、输出频率不受输入频率限制、输入功率因数可调等优点，成为近年来研究的一个热点[2-12]。矩阵变换器的研究对于开发高功率密度、高效率与高可靠性的电力变换系统具有重要意义，而且随着半导体技术的进步，在实际中将具有越来越广泛的应用场合。

矩阵变换器的控制分为直接变换法和间接变换法，其各有优点，但也不同程度地存在问题，适用于不同的场合。间接变换法是目前研究比较多而且很有前途的一种方法，它是将矩阵变换器等效为虚拟的交直和直交2个环节，从而可以应用现有的比较成熟的整流和逆变的各种调制方法[2]。相比于虚拟整流环节采用不控整流的调制方式，虚拟逆变环节采用SPWM方式是一种比较简单的控制策略[13]。但是该方法有2个不足之处：一是SPWM方式电压利用率低，不能满足实际场合对电压幅值的要求；二是虚拟直流环节没有储能元件，即使交流输入是对称电压，整流输出的虚拟直流电压也是有波动的，逆变环节直接应用SPWM输出电压的波形会有畸变。

本文为解决SPWM电压利用率低的问题，对虚拟逆变环节采用谐波注入PWM方式，即HIPWM（Harmonic Injected PWM）方式，又为了解决虚拟直流电压波动致使输出电压波形畸变的问题，在三相输入电压对称或非对称的情况下，针对虚拟整流环节输出的直流波动电压，推导了对虚拟逆变环节HIPWM的调制波进行补偿的补偿函数，通过对调制波调制比的补偿消除了直流电压波动对HIPWM输出的影响，保证了输出电压、电流波形的质量。最后应用MATLAB／Simulink进行了仿真，证明了所提出的控制策略的正确性。

1 矩阵变换器的拓扑结构及其等效拓扑

矩阵变换器的拓扑结构如图1（a）所示，由3行3列的开关组成一个3×3的开关矩阵。输入三相电压源 ua、ub、uc经过三相输入滤波器 Lf、Cf后，给变换器供电，变换后输出的三相电压uA、uB、uC供给三相负载。矩阵变换器的等效拓扑结构如图1（b）所示，由虚拟的整流环节和逆变环节组成。等效拓扑上的控制思想是首先对输入电压进行“整流”，以产生一个虚拟的直流环节，然后再对其进行“逆变”，逆变出所需频率和幅值的输出电压。

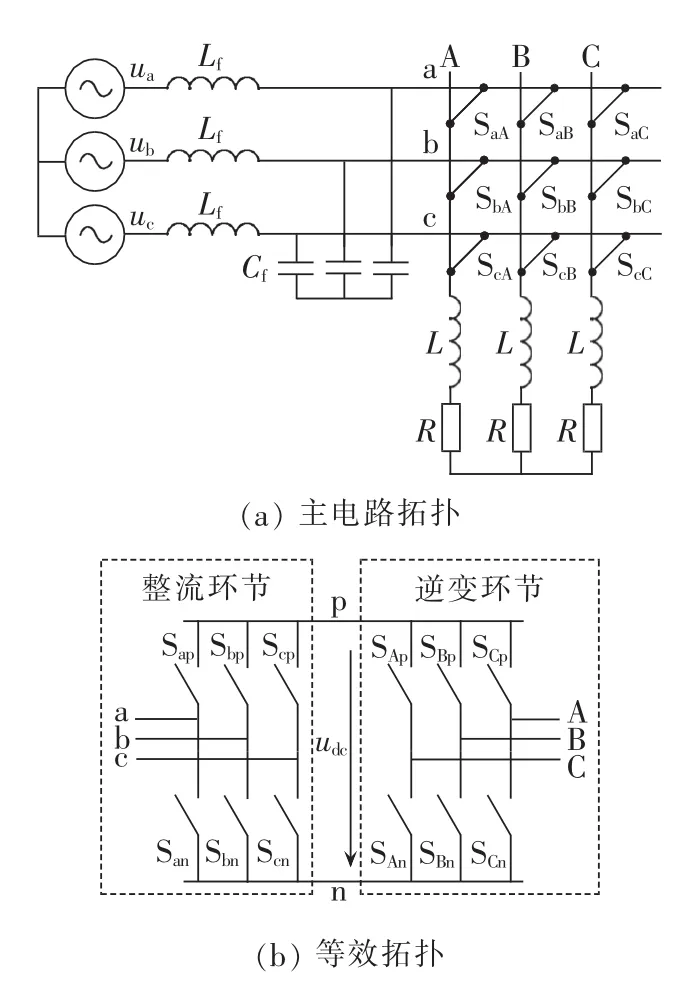
图1 矩阵变换器的拓扑Fig.1 Topology of matrix converter

2 矩阵变换器的HIPWM控制原理

为了简化控制策略，对整流环节采用不控整流调制方式，对应地要把输入电压划分为6个区间，如图2（a）所示；相应的整流输出的直流波动电压如图2（b）所示。

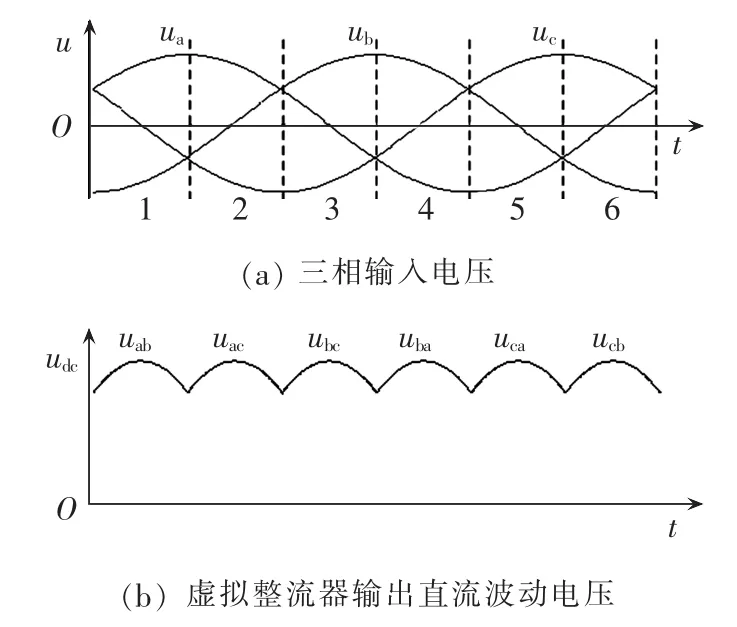
图2 三相输入电压和虚拟整流输出的电压Fig.2 Three-phase input voltage and output voltage of virtual rectifier

文献[13]给出了矩阵变换器的SPWM控制原理。HIPWM是为克服SPWM直流电压利用率低的缺点而提出的改进措施。在正弦参考信号中注入3次谐波，对输出基波电压没有不利影响，但形成了波顶较平坦的参考信号，相对于SPWM而言调制深度可大于1。只要参考信号最大值不超过载波峰值就不会进入非线性控制区，从而扩大了线性调制的范围。注入谐波的方法有很多，但是分析表明，各种注入方法所能改善的基波最大调制深度都为1.154[14]。而且随着注入谐波数的增加，计算会很困难，调制波的谐波分量变得复杂。鉴于此，本文采用只注入17%的3次谐波的方式，三相调制波的表达式为：

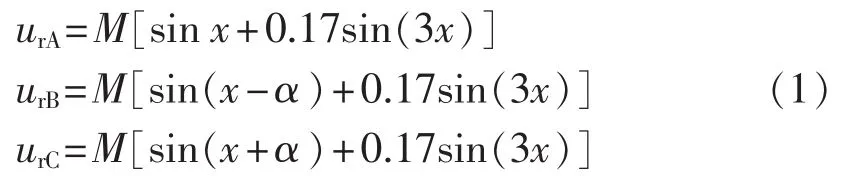
其中，x=ωot；α=2π／3；M 为调制比，其范围为 0≤M≤1.154。

按式（1）画出的调制波波形如图3所示。

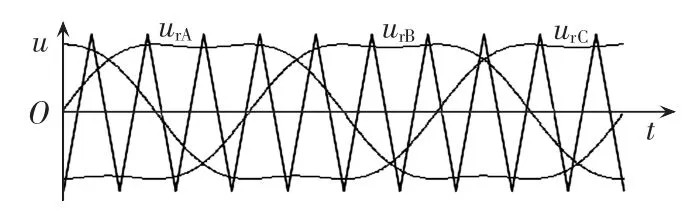
图3 注入3次谐波的三相调制波Fig.3 Three-phase modulation waves injected with third-order harmonic

三相调制波共用一个三角波作为载波，并分别与三角载波进行比较，输出3个等幅且宽度按调制波规律变化的脉冲序列来分别控制三相桥臂上的6个开关。矩阵变换器有9个双向开关，对虚拟整流环节采用不控整流调制方式，输出的直流波动电压有6种状态，在每一种状态下，等效逆变器三相桥臂上的6个开关对应矩阵变换器9个双向开关中的6个。如当输入电压在区间1时，整流输出的电压是uab，作为逆变器的直流输入电压，等效的电路如图4所示。

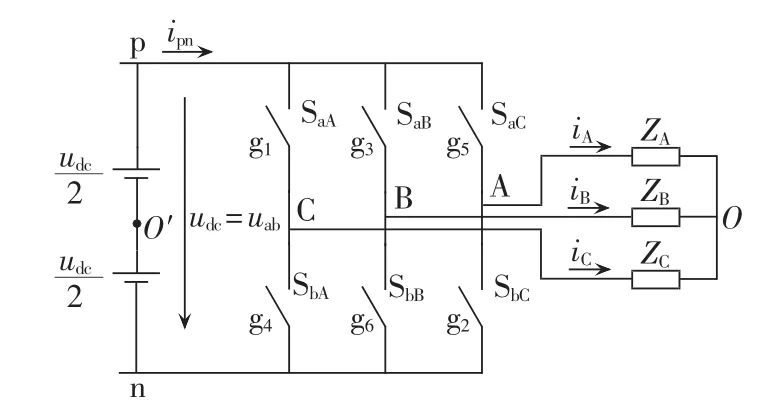
图4 等效逆变电路Fig.4 Equivalent inverter circuit

此状态下，等效逆变器三相桥臂上的6个开关g1、g2、g3、g4、g5、g6分别对应矩阵变换器的 SaA、SbC、SaB、SbA、SaC、SbB，而 ScA、ScB、ScC始终处于关断状态。 其余 5种状态下，g1、g2、g3、g4、g5、g6对应的开关见表 1。

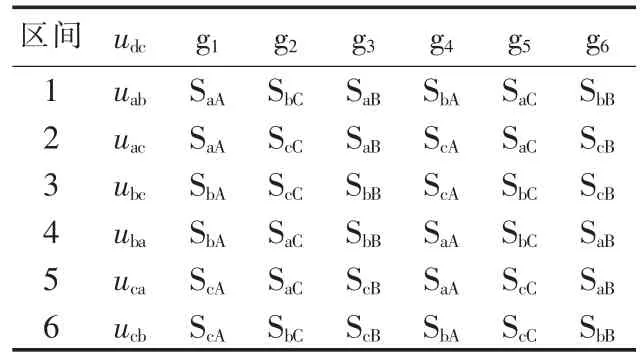
表1 虚拟逆变器对应的开关组Tab.1 Switch group of virtual inverter

3 HIPWM的调制波补偿函数的推导

由图2（b）可以看到，由于对整流环节采用不控整流调制方式，即使三相输入是对称电压，整流输出的虚拟直流电压udc也是有波动的。下面考虑一般情况，即三相输入电压可以是非对称的情况，对udc进行傅里叶展开，简化表示为：

下面对直流波动电压udc进行HIPWM的情况进行分析，从而推导出调制波的补偿函数。

图3中的三角波和调制波进行比较后，输出的脉冲序列可以看作为一开关函数，设开关函数为F，对F作傅里叶级数展开，表达式为[15]：

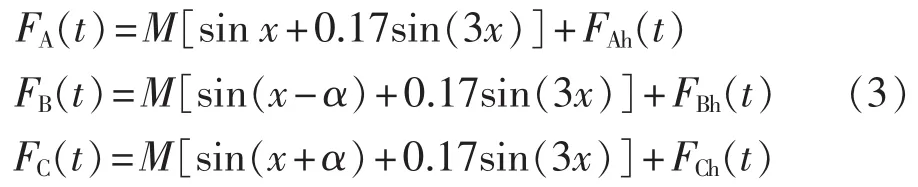
其中，FAh（t）、FBh（t）、FCh（t）是载波倍数频率及其附近的谐波分量。由于载波频率远大于调制波的频率，所以 FAh（t）、FBh（t）、FCh（t）是高频分量。 图 4 中 A、B、C三相桥臂输出端对直流侧电源中点O′点的电压为：

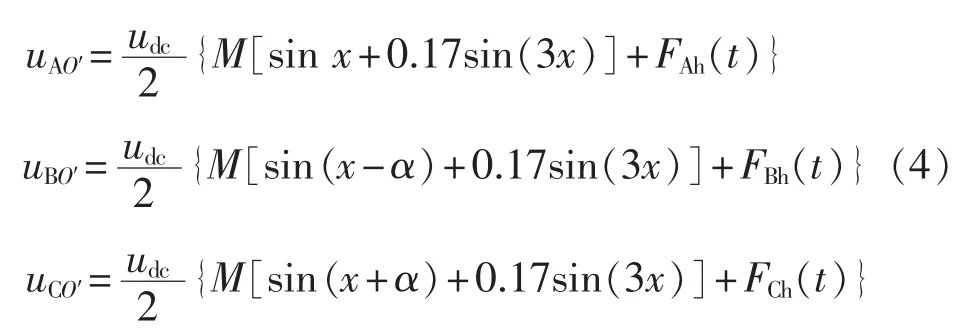
由文献[16]可知，三相桥臂输出的负载电压为：

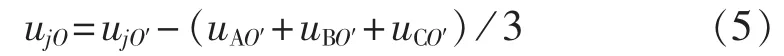
其中，jє｛A，B，C｝，将直流电压 udc的傅里叶表达式（2）和式（4）代入式（5）中并化简，可得三相负载电压为：

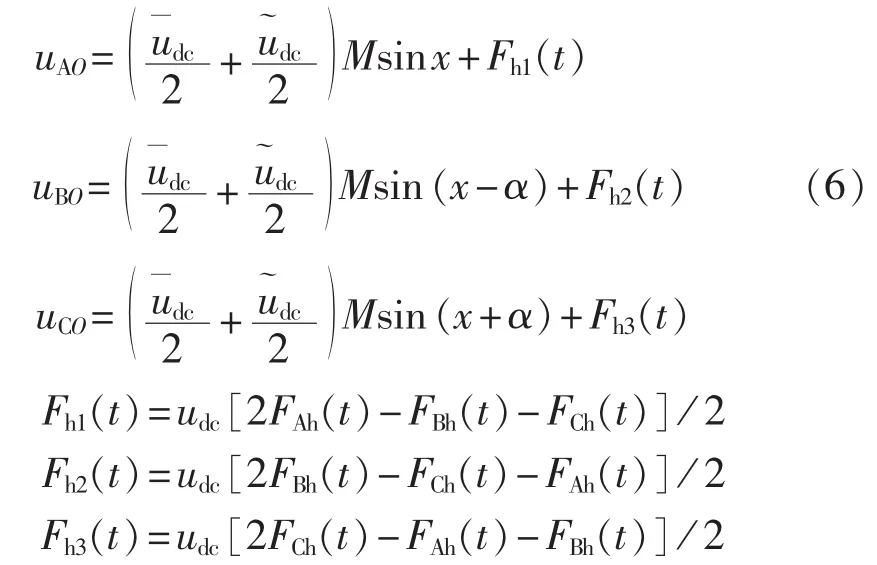
其中，Fh1（t）、Fh2（t）、Fh3（t）分别为各相开关函数中载波倍数频率及其附近的谐波分量的代数和，仍然为高次谐波。

由以上分析可知，各相负载电压由三部分组成，第一部分为直流电压经开关函数调制后输出的基波分量，第二部分为波动电压经开关函数调制后输出的低频分量和高频分量，第三部分为开关频率倍数附近的谐波分量。可见负载电压中含有除基波以外的低频分量，所以必须对三相调制波进行补偿，来消除由波动电压产生的低频和高频分量。在原三相调制波表达式（1）中分别加入函数项urAcom（t）、urBcom（t）和 urCcom（t），补偿后的各相调制波变为：

各相开关函数相应地变为：

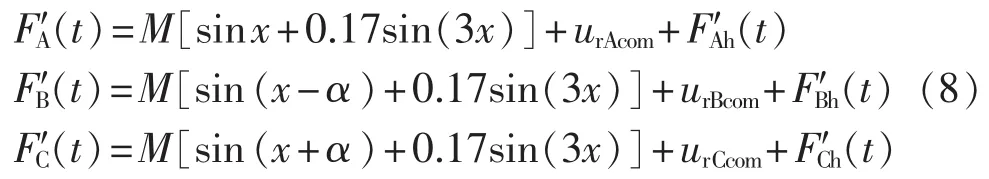
其中，F′Ah（t）、F′Bh（t）、F′Ch（t）是载波倍数频率及其附近的谐波分量。

A、B、C三相桥臂输出端对O′点的电压为：

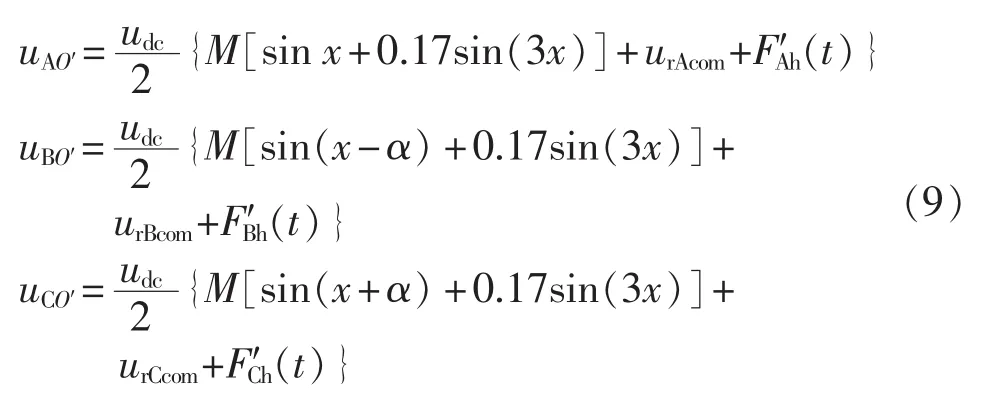
那么根据式（5）和（9）可以求得三相负载电压，其中A相负载电压为：

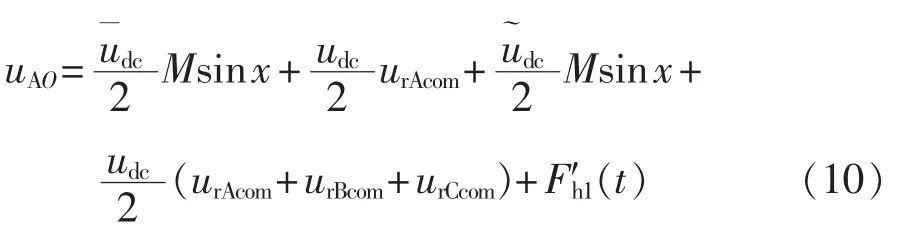
其中，F′h1（t） =udc[2F′Ah（t） -F′Bh（t） -F′Ch（t）]／2，为高次谐波。

式（10）中等号右边的第4项是三相调制波补偿函数调制输出电压的代数和，若不为0，它必然含有低频分量，则表示三相输出电压低频分量的调制是互相耦合的，这不是所希望的结果，所以该项必须等于 0，即：

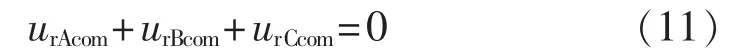
式（10）中等号右边的第1项是所期望输出的基波电压；第2项是补偿函数调制输出的电压，它是一个未知量；第3项是原调制波调制输出的含有低次谐波的电压项；第5项是高次谐波分量。对调制波进行补偿的目的就是为了消除原调制波调制输出的低次谐波电压，所以应该令第2项和第3项的代数和为0，即：

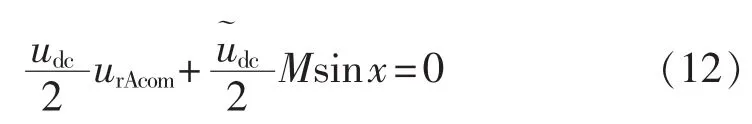
由式（12）可以求得A相调制波的补偿函数为：

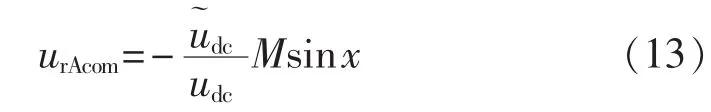
同理可以求得BC两相调制波的补偿函数为：

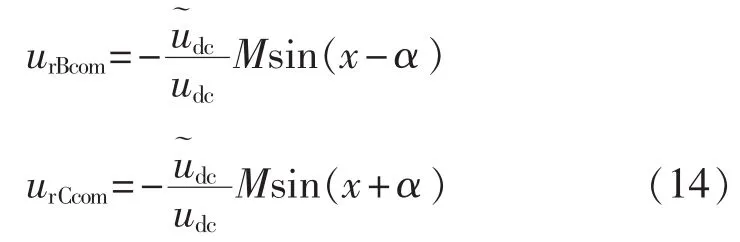
将三相调制波的补偿函数表达式代入式（11），可以验证式（11）成立，所以求得的三相调制波的补偿函数为有效解。经过补偿后，三相负载电压变为：

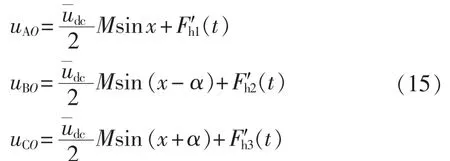
这说明补偿后，输出电压中除了基波电压外，只含有载波频率及其倍数附近的谐波分量。将式（13）、（14）代入式（7）中可以得到补偿后的调制波表达式：

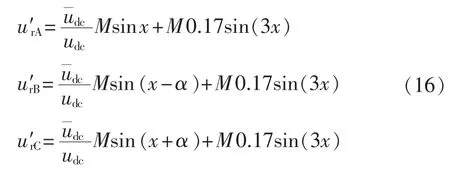
根据式（16）可知，只需把整流级输出电压udc的直流电压分量提取出来，便可以分别对各相调制波进行补偿。实际实现时，可以对三相输入电压进行不控整流，用模拟或数字滤波器提取直流电压分量，其硬件实现框图如图5所示。

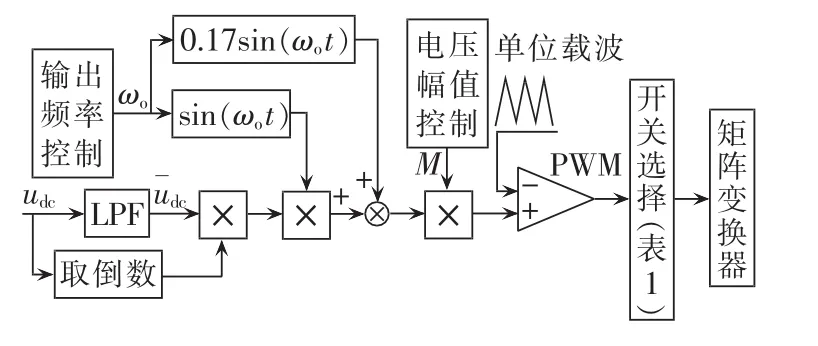
图5 硬件实现电路Fig.5 Hardware implementation circuit

4 电压增益分析

由式（17）可得：

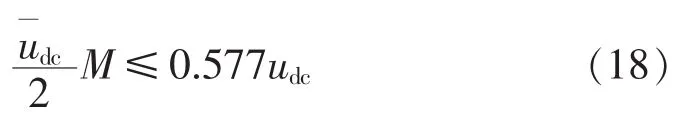
由上式可得，在输入电压三相对称情况下，输出相电压的最大幅值可以达到输出相电压幅值的0.866，达到了矩阵变换器理论上的最大电压增益；当输入电压非对称时，输出相电压幅值的最大值取决于整流级输出电压udc的最小值，其大小与输入电压的不对称程度有关。

5 仿真分析

本文基于MATLAB／Simulink建立了仿真模型，对提出的控制策略进行了仿真。仿真参数如下：负载为三相对称负载，每相电阻为5 Ω，电感为5 mH；输入电网频率为50Hz，输出三相电压频率为100 Hz；采样频率为10 kHz，仿真算法为Ode23t。

仿真针对2种情况进行。

情况1：对称三相输入电压，相电压幅值为311 V，输出相电压幅值设为可输出的最大值311×0.866≈269（V），仿真图形见图 6—8。

情况2：非对称三相输入电压，假设输入a相的电压正常，b相的相角有30°滞后，c相的幅值有20%的跌落。根据第4节的分析可以计算出，输出相电压的最大值约180 V，仿真图形见图9—11。

图6给出了情况1下补偿前后A相的调制波，其中虚线为补偿前的，实线为补偿后的，可见补偿后的调制波不再是标准的马鞍波。

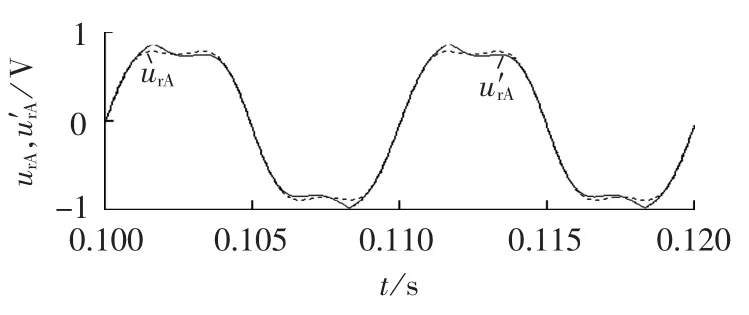
图6 补偿前后的A相调制波（情况1）Fig.6 Modulation waves of phase A before and after compensation（case 1）

图7给出了补偿前A相输出电压的波形及其频谱分析（由于B、C两相的谐波情况与A相相似，为了节省篇幅，B、C两相只给出仿真计算数据而不给出具体波形，下同）。由图7（b）给出的频谱，计算到80次谐波，A相输出电压THD为4.39%，B、C两相的THD分别为4.34%、4.32%。A相的基波幅值为268.7 V，B、C两相基波幅值分别为268.6 V、268.6 V。可见A、B、C三相的基波分量的幅值基本对称，三相输出电压的THD大小也基本相同。但是由图7（b）中的局部放大图可以看出，输出电压中含有较大幅值的低次谐波，不利于输出滤波器的设计。

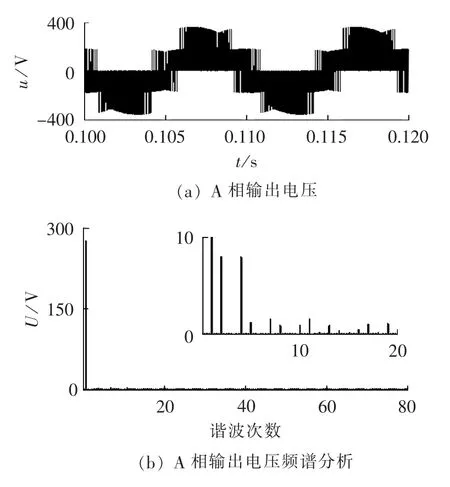
图7 补偿前A相输出电压及其频谱（情况1）Fig.7 Output voltage of phase A and its spectrum before compensation（case 1）

图8给出了补偿后A相输出电压的波形及其频谱分析。由图8（b）给出的频谱，计算到80次谐波，A相输出电压THD为1.32%，由局部放大图可见，其含有的低次谐波幅值都很小。B、C两相的THD分别为1.31%、1.25%。A相的基波幅值为269.5 V，B、C两相基波幅值分别为269.1 V、269.5 V。可见，正是由于对调制波的实时补偿，才使得三相输出电压基波分量的幅值基本对称，且低次谐波THD都大幅减小。

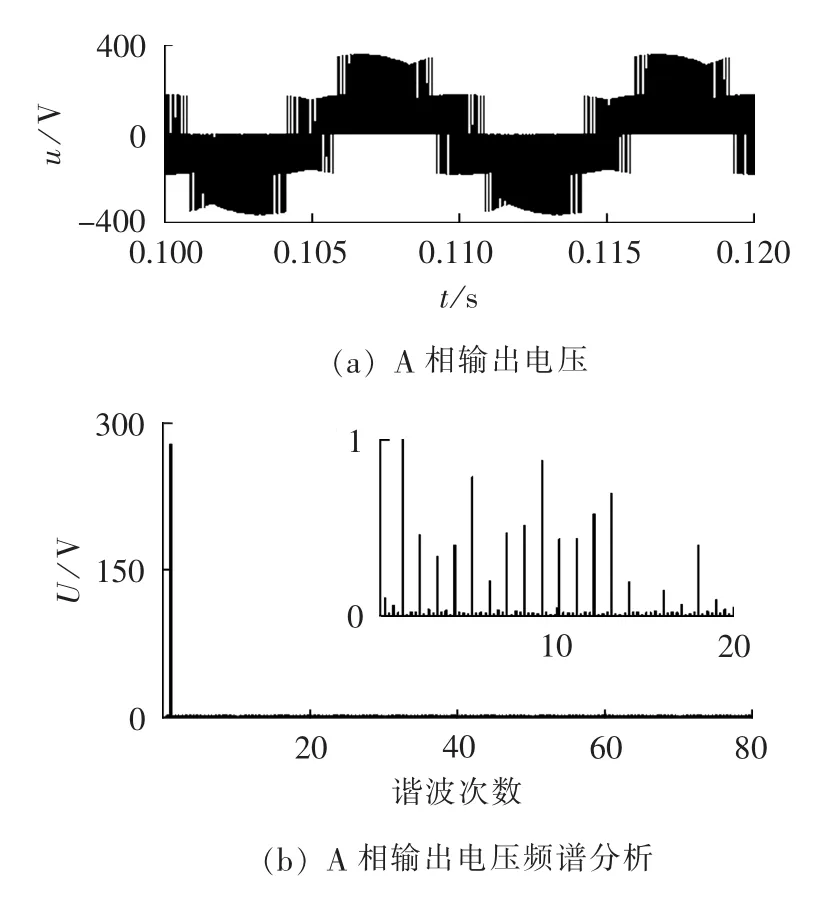
图8 补偿后A相输出电压及其频谱（情况1）Fig.8 Output voltage of phase A and its spectrum after compensation（case 1）

图9给出了情况2下补偿前后A相的调制波，其中虚线为补偿前的，实线为补偿后的。

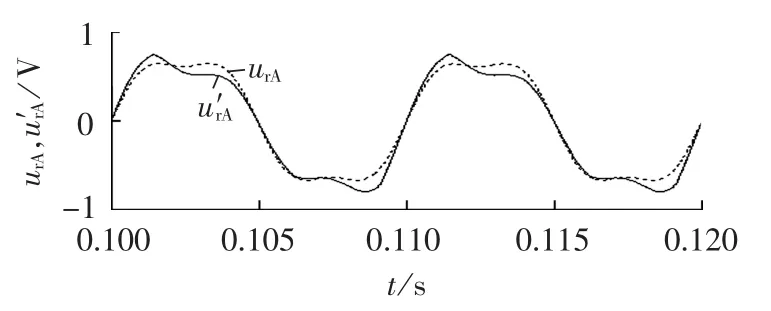
图9 补偿前后的A相调制波（情况2）Fig.9 Modulation waves of phase A before and after compensation（case 2）

图10给出了补偿前A相输出电压的波形及其频谱分析。由图10（b）给出的频谱，计算到80次谐波，A相输出电压THD为12.65%。由局部放大图可见，输出电压中不但含有较大幅值的低次谐波，而且还有直流分量。B、C两相输出电压THD分别为11.99%、13.84%。A、B、C三相输出电压的基波分量的幅值分别为181.1 V、176.6 V、181.5 V，可见输入电压的不对称还导致了输出电压基波分量的不对称。

图11给出了补偿后A相输出电压的波形及其频谱分析。由图11（b）给出的频谱，计算到80次谐波，A相输出电压THD为1.85%。由局部放大图可见，输出电压中含有低次谐波的幅值都很小。B、C两相输出电压THD分别为1.83%、1.66%。A、B、C三相输出电压的基波分量的幅值分别为180.2V、180 V、179.7 V，与期望的输出电压幅值基本相等，且三相基波电压基本对称。

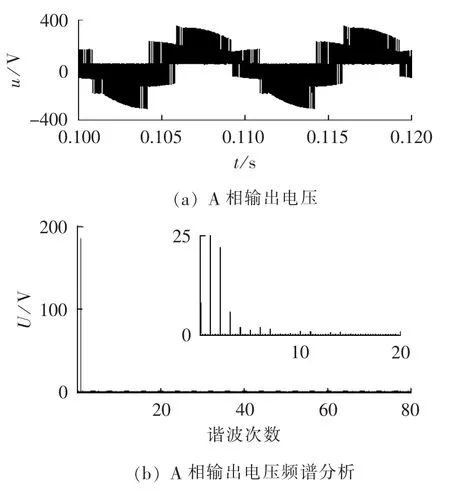
图10 补偿前A相输出电压及其频谱（情况2）Fig.10 Output voltage of phase A and its spectrum before compensation（case 2）

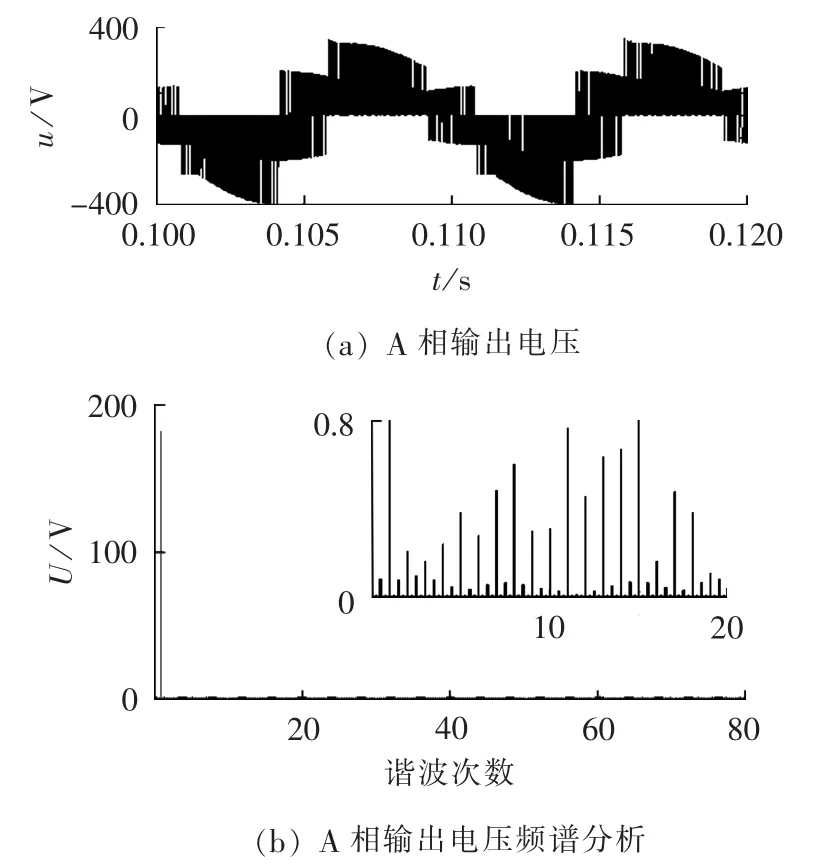
图11 补偿后A相输出电压及其频谱（情况2）Fig.11 Output voltage of phase A and its spectrum after compensation（case 2）

由上述仿真结果可以看出，当对调制波进行补偿后，无论输入电压是在对称还是非正常的情况下，总能输出电压对称的三相电压，且其低次谐波含量非常小。当三相输入电压对称时，设定电压增益为理论上的最大值0.866，输出电压中没有幅值较大的低次谐波，这说明基于补偿函数HIPWM策略的电压增益可以达到0.866的理论分析是正确的。

6 结论

矩阵变换器是交交直接变换器，不但控制算法复杂而且无中间储能环节，输入电压的波动会造成输出电压、电流的畸变。本文提出了一种基于补偿函数的HIPWM控制策略，该控制策略对等效模型的整流级采用不控整流方式，对逆变级应用基于补偿函数的HIPWM策略。此方法的优点是：控制简单、计算量小、易于硬件实现，尤其是对输入电压非正常情况同样适用。