不平衡电网电压下DFIG双SRF控制策略
2013-10-10刘会金
肖 辉,刘会金
(1.武汉大学 电气工程学院,湖北 武汉 430072;2.长沙理工大学 电气与信息工程学院,湖南 长沙 410004)
0 引言
由于风能资源分布的特殊性,风力发电多位于偏远地区,通常需要较长的电力传输线来输送风电场的电能,这一方面使得风电场接点处电网相对较为薄弱;另一方面由于电网各阻抗的不对称性、线路破损、绝缘老化等原因,会在风力发电机接点处出现不平衡现象[1-2]。电网电压的不平衡给电机的正常运行造成影响,如损耗增大、发热增多、转矩脉动以及转矩脉动引起的齿轮箱和机械传输轴的疲劳损耗、无功功率脉动等,如不采取相应的控制措施,这些不平衡影响会进一步恶化电网电压[3-4]。因此,对交流发电机而言,当电网电压不平衡度达到一定值(如6%)时,风力发电机将从电网切出[5]。事实上,大多数接入分布式发电系统的风力发电机在电网不平衡度超过2%时,就已经脱离了电网[6]。对双馈型风力发电机而言,由于其定子直接与电网相连,因此电网电压的不平衡也会直接影响到双馈电机的运行状态。
在电网电压不平衡条件下如何控制双馈电机的运行,目前关于这方面的研究策略可概括为3类:第1类即通过在双馈电机的定子接入回路中引入串联变流器,以克服电网电压不平衡对双馈电机定子端电压的影响[7-10];第2类即通过网侧变流器的控制使其具有STATCOM特性,以对定子电压进行补偿,克服电网电压不平衡对双馈电机定子端电压造成的影响[11];第3类即通过控制双馈电机转子电流或转子电压,从双馈电机本身的控制实现双馈电机的抗电网电压不平衡运行特性[12-13]。由于第1类、第2类不平衡控制策略没有直接涉及双馈电机本身的运行特性和相应的控制策略,因此本文对双馈电机第3类不平衡控制策略进行研究,应用对称矢量法在双同步旋转坐标系(SRF)下分析了电网电压不平衡情况下双馈电机的运行特性,进而在此基础上对电网不平衡条件下双馈电机的双SRF控制方案进行深入研究。
1 电网电压不平衡情况下双馈电机运行状况分析
1.1 不平衡度定义
对于三相不平衡系统,其不平衡的程度通常用不平衡度进行表示。三相电量不平衡度通常用负序分量与正序分量的百分比表示,即[14]:
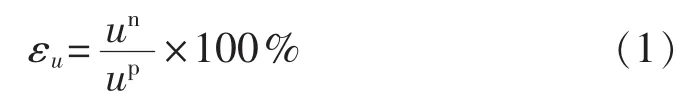
而上述定义不便于实施现场的测量与计算,为了便于实际操作,本文采用不平衡度相量定义的简化标量形式:
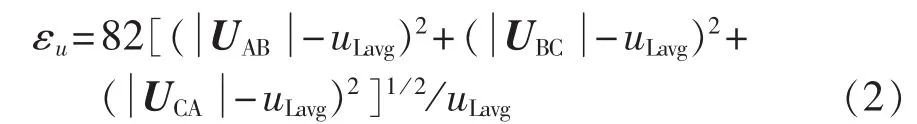
1.2 双馈电机在电网电压不平衡情况下的运行状况分析
在电网不平衡状况下采用对称分量法对双馈电机的工作状态进行分析。正序电压加在定子绕组上产生正序电流,此电流产生与转子同向旋转的旋转磁场;负序电压加在定子绕组上产生负序电流,并激励一个与转子旋转方向相反的旋转磁场[15]。由于双馈电机通常不含有中线,故本文在分析时不考虑零序分量的影响。
通过对称分量法可将双馈电机的电路等效为正序电路和负序电路之和的形式,并且在各自的电路中均保持为三相平衡的状态。因此,与电网平衡时的分析类似,电网不平衡条件下双馈电机的运行分析可分别在正序 SRF(dpqp)和负序 SRF(dnqn)中进行,可分别得到正、负序SRF中双馈电机的数学模型。其中,Upsdq、Unsdq分别表示正、负序SRF中定子电压的正、负序分量;Urpdq、Urndq分别表示正、负序SRF中转子电压的正、负序分量;Ipsdq、Insdq分别表示正、负序SRF中定子电流的正、负序分量;Irpdq、Irndq分别表示正、负序SRF中转子电流的正、负序分量;ψpsdq、ψnsdq分别表示定子磁链的正、负序分量;ψprdq、ψnrdq分别表示转子磁链的正、负序分量。
正序SRF中,双馈电机的数学模型可表述为:

负序SRF中,双馈电机的数学模型可表述为:
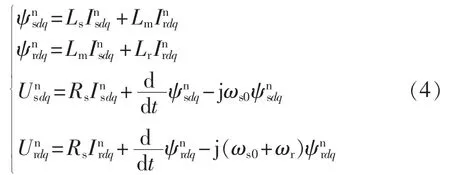
根据正、负序SRF与abc静止坐标系之间的关系,可将静止坐标系中的正序电压矢量和负序电压矢量分别表示为:
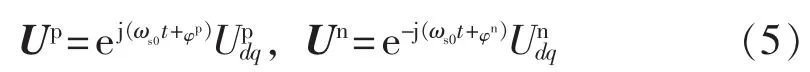
其中,Up、Un分别表示abc静止坐标系中正序电压矢量和负序电压矢量。
因此,在电网电压不平衡条件下,定子的电压矢量Us可表示为:
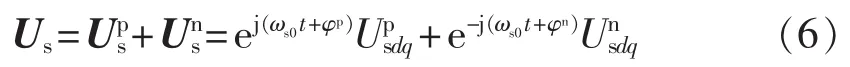
同理可得定子的电流矢量Is为:

在电网不平衡情况下,采用等量坐标变换,得到双馈电机定子侧复功率为:

将式(6)、(7)代入式(8)得:

其中,Ps0、Qs0分别表示定子侧有功功率、无功功率的平均值;Psc2、Pss2、Qsc2、Qss2分别表示双馈电机定子侧有功功率和无功功率的2次脉动量的幅值,其脉动频率为 2ωs0。
式(9)表明,当双馈电机运行于电网不平衡条件下时,定子侧有功功率和无功功率出现明显的2次脉动量。 式(9)中 Ps0、Psc2、Pss2、Qs0、Qsc2、Qss2与定子电压、电流量的关系可表述为:

上式表明,要消除有功功率和无功功率的2次脉动量,等式[Psc2Pss2Qsc2Qss2]T=0 必须成立,则双馈电机定子电流矩阵[ipsqipsdisnqisnd]T仅有零解。 即当双馈电机在电网不平衡条件下运行时,在定子侧有功功率和无功功率一定的前提下,存在唯一一组定子电流可以消除其有功功率的脉动量或者无功功率的脉动量,但二者不能同时被消除。
由于双馈电机定、转子之间的磁场耦合作用,使得双馈电机的转子电压和转子电流中含有频率为ωs0+ωr谐波成分。与定子侧分析类似,可得到转子侧有功功率和无功功率如下:

其中,Pr0、Qr0分别表示转子侧有功功率、无功功率的平均值;Prc2、Prs2、Qrc2、Qrs2分别表示双馈电机转子有功功率和无功功率的2次脉动量的幅值,其脉动频率为 2ωs0。
上式表明,双馈电机在电网不平衡条件下运行时,其转子侧功率中也出现2次脉动量,脉动频率为100 Hz。
在忽略损耗的情况下,双馈电机的电磁转矩可表述为:
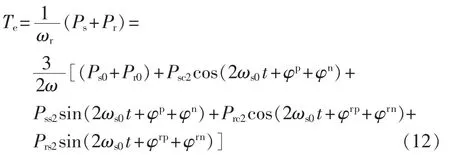
可见,通过控制双馈电机转子侧功率2次脉动量的幅值和相位,便可以减小甚至消除双馈电机电磁转矩的2次脉动量。
由以上分析可以看出,双馈电机在电网不平衡条件下运行时,若不采取任何不平衡控制措施,则定、转子侧有功功率和无功功率以及电磁转矩中均会出现2次脉动量,而且可以证明,发电系统总的发电功率也会出现明显2次脉动量,并且2次脉动量所占的比重会随着电网不平衡度的增大几乎是线性地增大;其电磁转矩2次脉动量与无功功率的2次脉动量具有一致性,若采取措施可以同时消除。另外,对于双馈型风力发电机而言,由于其机械惯性时间常数较大,因而转速的2次脉动量较小,消除电磁转矩2次脉动量的同时,也必将削弱双馈电机的机械输入功率中的2次脉动量,因而即便双馈电机的定子侧仍然有较大的有功功率2次脉动量,但就整个风力发电系统而言,因电网不平衡所造成的系统发电功率的2次脉动量得到了改善。
就双馈电机的不平衡运行而言,主要有以下几种控制目标:获得平衡的定子电流,以确保双馈电机定子绕组具有平衡的发热量;消除定子侧有功功率的2次脉动量;消除电磁转矩的2次脉动量,以减小机械应力;消除转子电流的振荡,以使转子变流器安全运行。在实际应用中可结合不同的控制要求选取相应的不平衡控制目标。
2 双SRF控制系统设计
电网电压负序分量的存在,使得定子侧有功功率和无功功率以及电磁转矩均出现了2次脉动量,而提高双馈电机不平衡运行能力的关键就是,通过对转子侧电压和电流进行控制,以产生相应的转子电压和电流量,从而实现所设定的控制目标。
双SRF控制是依据对称分量法,根据双馈电机在正、负序SRF中的数学模型式,分别在正、负序SRF中对转子电流的正序、负序量进行控制,其中转子电流正序量的参考量由双馈电机平均有功功率(平均电磁转矩)和平均无功功率的控制作用进行设定,而转子电流负序量则由相应的不平衡控制目标进行设定。
对正序 SRF(dpqp)和负序 SRF(dnqn)分别采用正序定子电压矢量定向和负序定子电压矢量定向,则有:
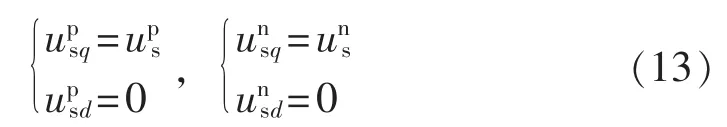
由双馈电机在正、负序SRF中的磁链模型式可得:
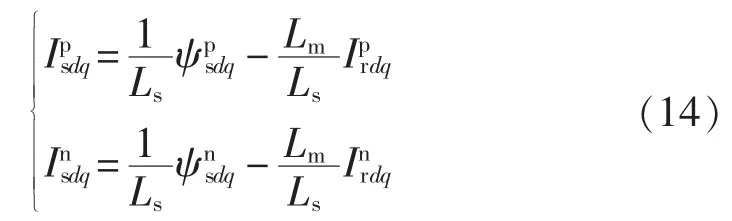
将式(13)和式(14)代入式(10)得定子无功功率的2次脉动量的幅值为:
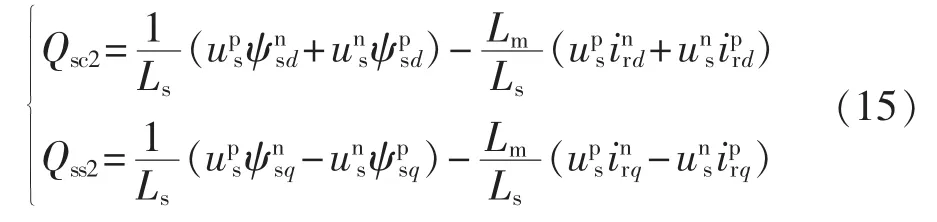
由式(15)不难看出,当转子电流的正序量iprq和iprd分别用作定子侧有功功率的平均值Ps0(或电磁转矩的平均值Te0)和无功功率的平均值Qs0控制时,可以通过对转子电流的负序量(inrd和inrq)进行控制,以实现对定子侧无功功率2次脉动量的幅值(Qsc2和Qss2)的控制。而通过对Qsc2和Qss2的控制,也间接实现了对电磁转矩2次脉动量(Tes2和Tec2)的控制。
令式(15)中的 Qsc2=0、Qss2=0,并根据不平衡度的定义,可得到:

将式(16)代入转子电流矢量,可得为实现Qsc2=0、Qss2=0的控制目标所需转子电流幅值的最大值为:
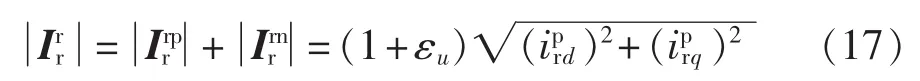
上式表明:在iprd、iprq一定的情况下,转子侧电流的幅值随着电网电压不平衡度εu的增大而增大,这就决定了在电网电压的不平衡度达到一定程度,即超出了双馈电机转子变流器的设计容量时,双馈电机必须降载运行,甚至脱离电网。
根据双馈电机在正序SRF中的电压表达式(3)可对dpqp坐标系中的控制进行设计。若采用PI调节器,并令PI调节器的输出控制转子电压方程式(3)中转子电流的动态项,可得dpqp坐标系中转子电压的控制方程为:

同理,根据负序SRF中转子电压表达式(4)可对dnqn坐标系中的控制进行设计,采用同样的控制规律,可得dnqn坐标系中转子电压的控制方程为:
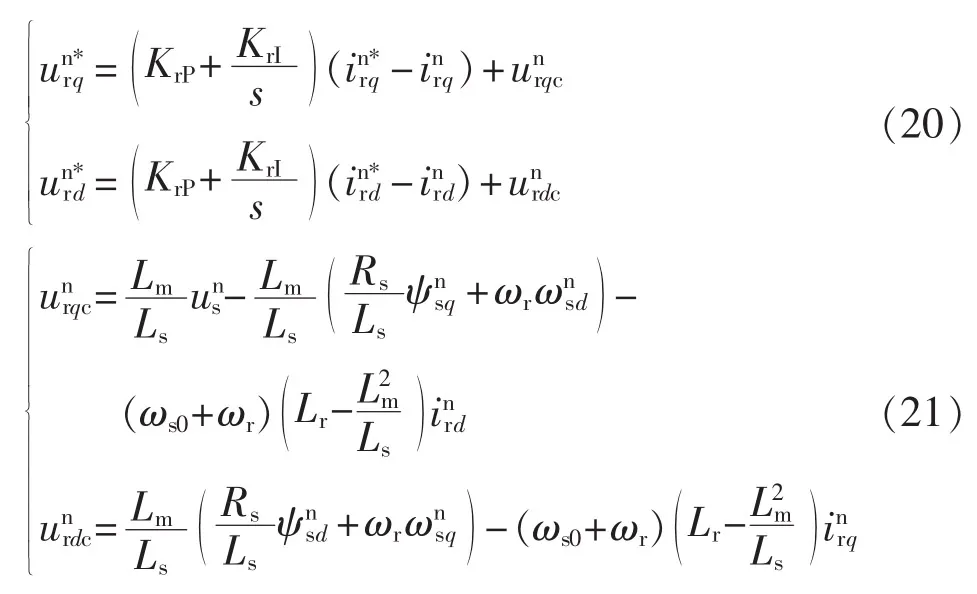
据此,可以设计在电网电压不平衡时双馈电机的双SRF控制结构图如图1所示。
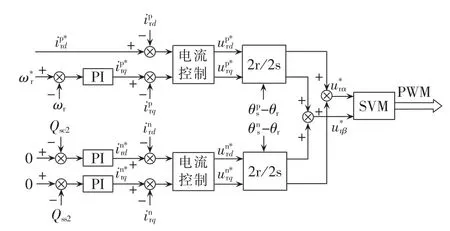
图1 双SRF控制结构Fig.1 Structure of double SRF control
3 坐标系定向及正、负序电气量的检测
要实现图1所示的双SRF控制结构,首先应解决的问题就是定向角度θps、θns和正、负序SRF中的定子电流(ipsd、ipsq、insd、insq)、定子电压(upsd、upsq、unsd、unsq)以及转子电流(iprd、iprq、inrd、inrq)的检测问题。
在正序SRF中,三相不平衡电压矢量可表述为:

显然,在正序SRF中三相不平衡电压矢量为直流量和2次脉动量之和,因此三相不平衡情况下正、负序SRF的定向可以用图2进行描述。
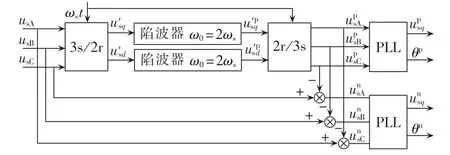
图2 正、负序SRF的定子电压定向Fig.2 Stator voltage orientation in positive and negative sequence SRFs
同理,在正、负序SRF中定子电流矢量Ips、Ins可表述为:
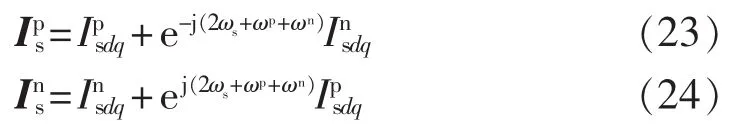
根据式(23)、(24)可设计正、负序 SRF 中定子、转子电流量的检测方案如图3、图4所示。
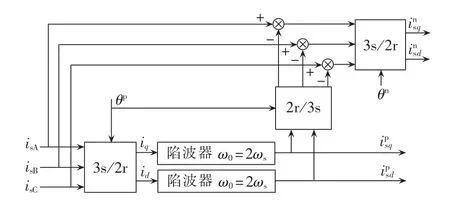
图3 正、负序SRF中定子电流量的检测Fig.3 Stator current detection in positive and negative sequence SRFs

图4 正、负序SRF中转子电流量的检测Fig.4 Rotor current detection in positive and negative sequence SRFs
4 系统仿真研究
为验证电网电压不平衡情况下双馈电机的双SRF控制的性能,本文对所设计的控制系统在仿真软件EMTP-RV中进行了建模和仿真研究。仿真模型采用某实际风电场数据,该风电场由17台1.5 MW的双馈风力发电机组成,分为5台、7台、5台3组,其出线端接公共母线,然后经过690 V/35 kV的升压变压器接入系统。110 kV侧系统经过121 kV/35 kV降压变压器与风机出口端的升压变压器的35 kV侧相连接。线路为LGJ-300,线路阻抗为R+j X=1.972+j7.777 Ω,110 kV系统母线的最小短路容量为1 351 MV·A,系统阻抗为8.96 Ω。仿真时所选电网电压不平衡度为10%。该风力发电系统接线图如图5所示。
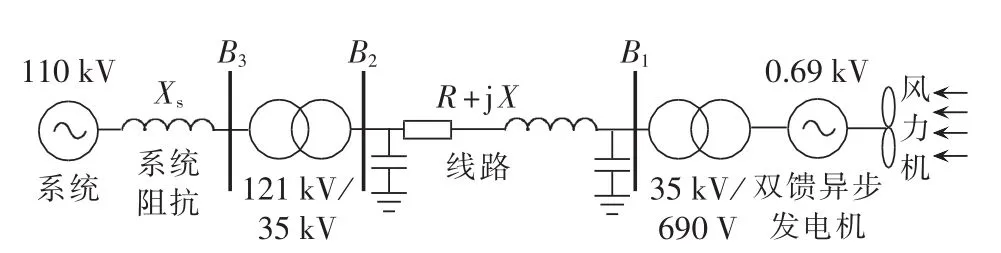
图5 双馈风力发电系统接线示意图Fig.5 Wiring diagram of DFIG wind power system
仿真时设置电网电压只含正序基波电压和负序基波电压,且电网三相电压不平衡度为10%。仿真时间设置为10 s,仿真步长为50 μs。通过仿真分析得出常规矢量控制策略和双SRF控制策略下,定子侧无功功率、电磁转矩和总机械功率波形分别如图6(a)—(c)和(d)—(f)所示。 对比发现,以消除定子侧无功功率Qs中的脉动量Qsc2和Qss2为控制目标,采用双SRF控制方案后,定子侧无功功率Qs、电磁转矩Te和总机械功率Pm的2次脉动量均得到了较好的抑制。
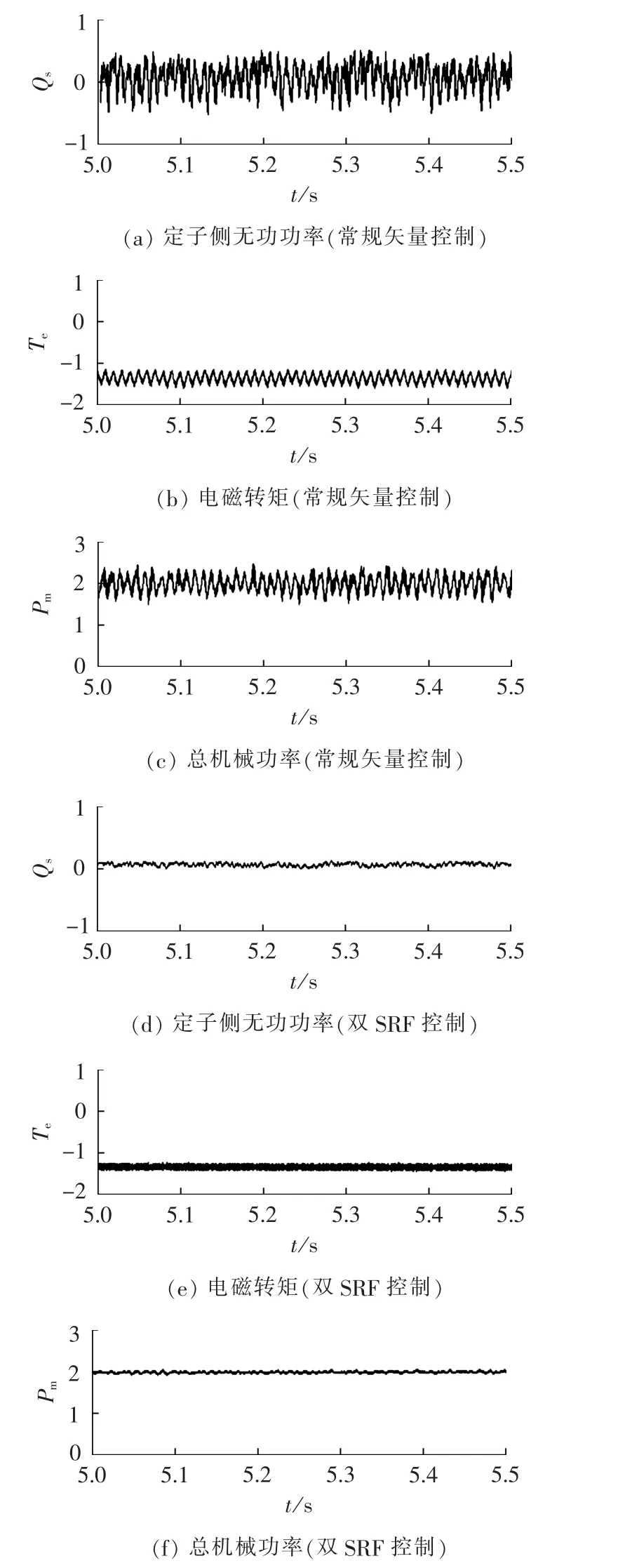
图6 常规矢量控制和双SRF控制策略下仿真波形对比Fig.6 Comparison of simulative waveforms between normal vector control and double SRF control
在不平衡电网电压条件下,针对双馈电机常规控制策略和双SRF控制策略下得出的定子侧无功功率、电磁转矩和总机械功率波形进行FFT谐波分析,得出频谱图分别如图 7(a)—(c)和(d)—(f)所示。由图 7(a)—(c)可以明显看出,发电机定子侧无功功率中除了包含直流分量外,还包含100 Hz、200 Hz、300 Hz等偶数倍频率的分量;总机械功率和电磁转矩中除了包含直流分量外,还包含100 Hz的分量。即在电网电压不平衡情况下,采用常规的矢量控制策略,会产生2次脉动分量。由图7(d)—(f)可以看出,在电网不平衡条件下,双馈电机采取双SRF控制策略后,发电机定子侧无功功率、电磁转矩和总机械功率中都只包含直流量,2次脉动量得到了很好的抑制。
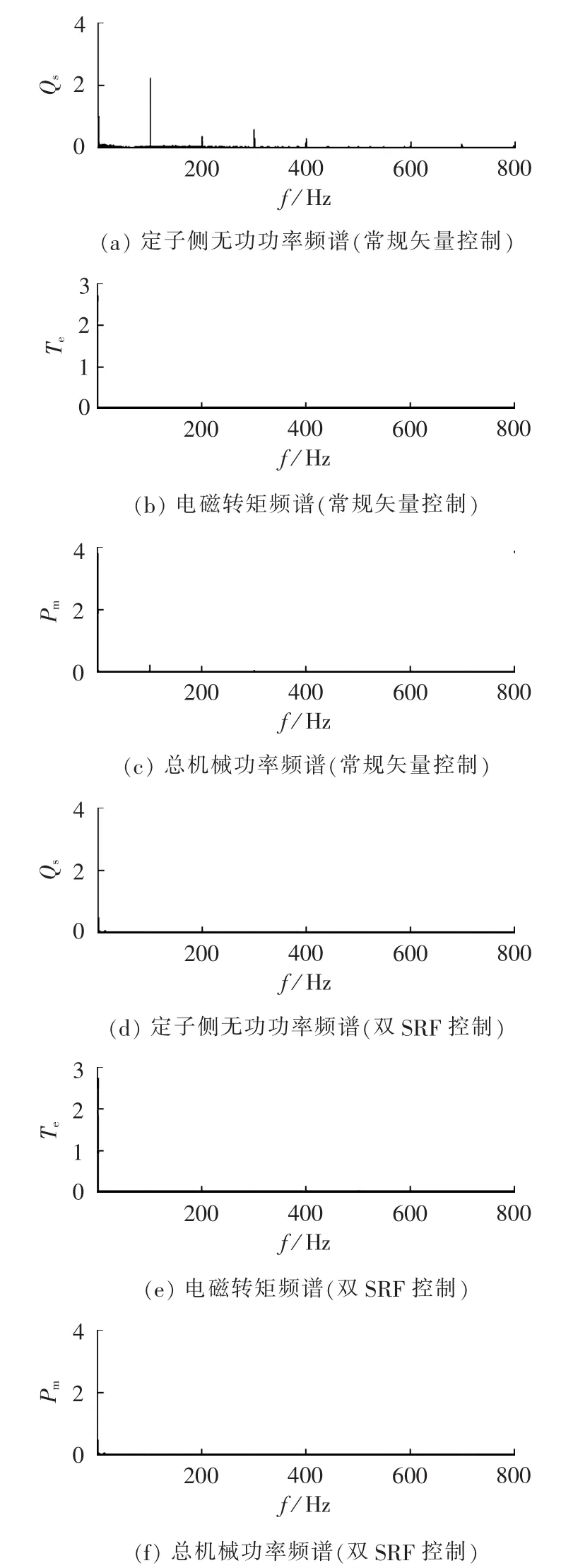
图7 常规矢量控制策略与双SRF控制策略下各量的FFT谐波分析对比Fig.7 Comparison of FFT between normal vector control and double SRF control
5 结论
本文对电网电压不平衡条件下双馈电机特性进行了理论分析,针对双馈电机不平衡控制策略进行了研究,提出一种双SRF控制策略。理论分析和仿真结果表明,所提策略可有效抑制电网电压不平衡情况下引起的定子侧无功功率、电磁转矩和总机械功率的2次脉动量,实现双馈风力发电机组的稳定运行。
