基于LMS的加速收敛步长选择原理与自适应三相电网谐波检测

刘传林，刘开培

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.广东水利电力职业技术学院 自动化工程系，广东 广州 510635）

0 引言

随着抑制电网谐波提高电能质量技术的进一步发展，谐波检测的动态响应和稳态精度要求也随之提高。首先，常规检测方法虽有成熟的应用，但都有待改进，如目前广泛应用的基于瞬时无功功率理论的检测方法，其中ip-iq运算的谐波电流检测方法具有较好的检测速度和精度[1-2]，并不断得到改进[3-4]。其次，自适应方法具有良好的自适应性和鲁棒性，逐渐在谐波检测中得到广泛应用[5-7]。基于最小二乘LMS（Least Mean Square）的自适应检测系统性能可以从初始收敛、跟随性能与稳态精度3个方面衡量算法的优劣[8]，选择较小的LMS算法迭代步长μ可得到更好的自适应检测稳态精度，但会降低自适应的收敛速度和跟随性能，因而常规固定步长的LMS自适应算法在收敛速度、跟随性能与稳态精度方面对迭代步长μ的要求是矛盾的。如果采用固定步长的自适应算法，则检测性能会受到限制[9]。对此，学者们基于LMS提出了许多调整迭代步长的自适应算法[10-11]，可以改善自适应谐波检测的性能。

为了兼顾自适应电网电流检测的收敛速度与稳态精度，基于LMS的自适应算法都依据经验选择变步长的策略：当离最佳值较远时选择较大的迭代步长，而为了保证电流检测的稳态精度，在偏离最佳值近时选择较小的迭代步长。在LMS自适应理论的基础上，本文为阐明提高收敛速度与稳态精度而如何选择步长的策略，对基于经验直觉而选择算法的迭代步长进行理论定量研究。同时在此基础上进一步提出新的兼顾快速收敛与稳态精度的变步长算法，结合基于瞬时无功功率理论ip-iq运算的谐波电流检测，应用新的变步长LMS算法构建自适应电网三相谐波检测系统，并进行了仿真研究。

1 基于LMS的自适应电流检测系统

由离散LMS算法构成的自适应电流检测系统如图 1 所示[9]。

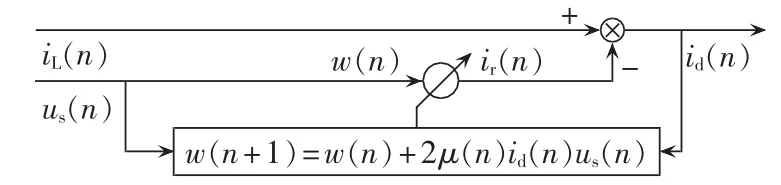
图1 基于LMS算法的自适应电流检测原理Fig.1 Schematic diagram of adaptive current detection based on LMS algorithm

在基于LMS算法的自适应电网电流检测中，设离散的迭代步长为μ，有：

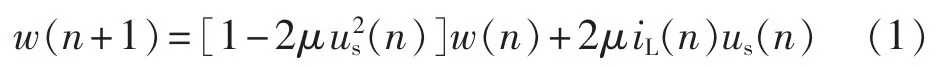
取数学期望为：

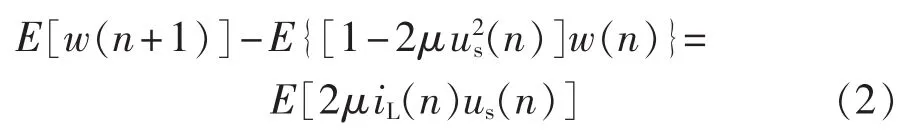
设LMS中μ取值小，且独立存在近似不相关的条件为：

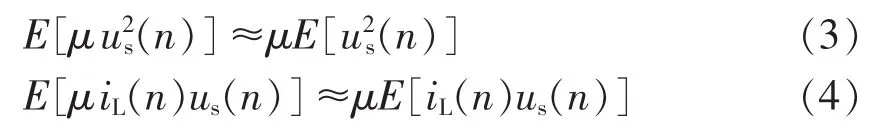
得：

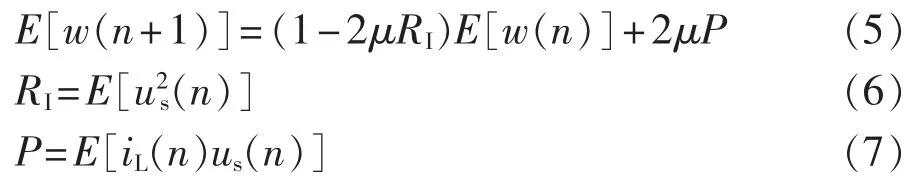
其中，RI与P分别为u2s（n）、iL（n）us（n）的数学期望。

设稳态条件下电流检测的最佳权值为w*。当时系统到达平衡状态的最佳权值为w*，则有：

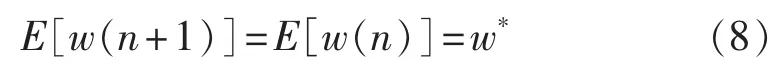
即LMS检测系统的最佳权值为：

在基于LMS迭代算法的过程中，系统的权值瞬时偏差为：

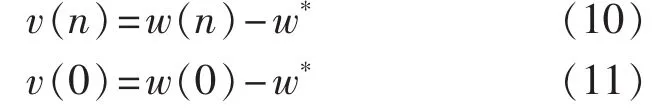
因此在不考虑计算噪声的条件下，当n∞时得到：

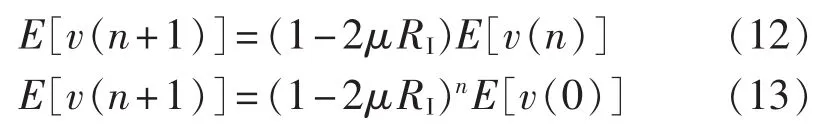
LMS算法的收敛条件为：

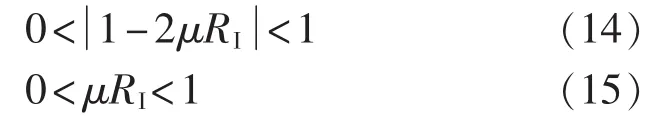
LMS算法中，迭代过程不可避免地存在噪声效应。为明确算法问题的本质，研究检测算法对一确定系统进行自适应搜索过程，设基于LMS算法的迭代步长为μ，则由自适应原理得：

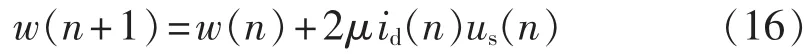
不考虑计算噪声的条件时：

考虑梯度估计受噪声δN（n）的影响，即考虑在对w*自适应调节过程中有：

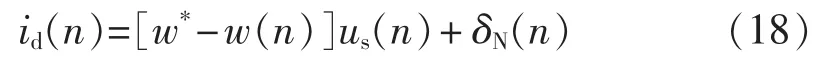
则：

确定等式的数学期望，有：

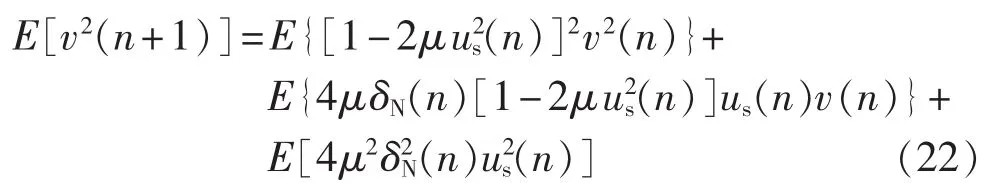
通常LMS算法中，μ一般足够小，因此v2（n）本质上独立于 us（n），则近似有：

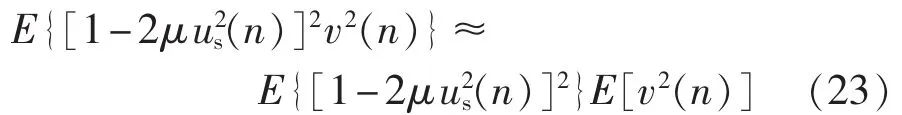
因 δN（n）是零均值，E[δN（n）]=0，独立于 us（n）、v（n），则：

2 LMS算法加速收敛的步长选择原理

一般地，基于LMS算法的自适应系统中应采取当偏离最佳值较远（方均误差（MSE）较大）时选择较大步长、而MSE较小时选择较小步长的策略[11-12]。

定理：在满足收敛条件的LMS算法中，当离最佳值较远时，要提高算法迭代收敛速度的充要条件是选择步长较大的迭代步长，即选用较大迭代步长的收敛速度快于较小迭代步长的收敛速度。反之亦然。证明如下。

a.充分性。

在式（26）中，令 RⅡ=E[us2（n）]，RⅣ=E[us4（n）]，则有：

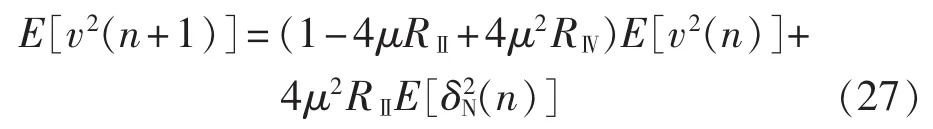
即当 LMS 算法迭代步长满足 μ∈（0，μmax），且第 n次迭代前为 E[v2（n）]时，式（27）表明经第 n 次迭代后 E[v2（n+1）]与 E[v2（n）]的关系式。

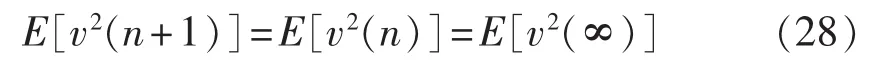
代入式（27）得：

E[v2（∞）]μ反映步长为 μ 的 LMS 算法稳态条件下的最佳收敛。 且第 n次迭代前，E[v2（n）]仍远离最佳值 E[v2（∞）]，即在步长为 μ 的条件下：

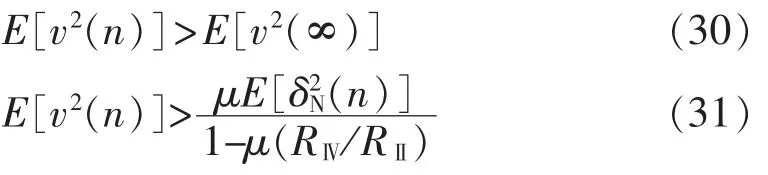
取 μ=μ1+μ2，μ1、μ2∈（0，μmax），μ1＞μ2，则有：

由于 1-μ（RⅣ／RⅡ）＞0，1-（μ1+μ2）（RⅣ／RⅡ）＞0，得：

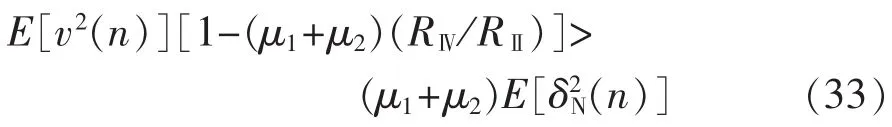
不等式两边同乘（μ1-μ2），由于 μ1＞μ2＞0，故 μ1-μ2＞0，则有：

展开得：

在式（36）两边同乘 4 并且同时加 E[v2（n）]项，根据式（28），有：

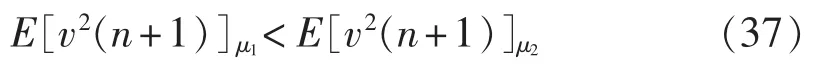
即经第 n 次迭代后，步长大的 E[v2（n+1）]μ1小于步长小的 E[v2（n+1）]μ2，算法收敛速度更快。

b.必要性。

LMS 算法中，设 μ1、μ2∈（0，μmax），μ=μ1+μ2，且第n 次迭代前，v（n）平方数学期望为 E[v2（n）]，仍远离最佳值 E[v2（∞）]，E[v2（n）]＞E[v2（∞）]，则经第 n 次迭代后，有：

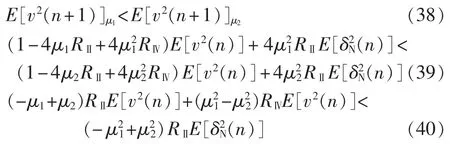
反设 μ1＜μ2，故 -μ1+μ2＞0，则有：

即：

与所设达到稳态前远离最佳值E[v2（∞）]的条件 E[v2（n）]＞E[v2（∞）]矛盾，故期望 E[v2（n+1）]μ1＜E[v2（n+1）]μ2必有 μ1＞μ2。

结论表明：在满足收敛条件的LMS算法中，迭代运算中如果当前权值远离最佳值，选择较大的迭代步长的收敛速度优于选择较小步长的收敛速度。定理在理论上给出了定量的解释，且与物理上的判断是一致的。

3 基于ip-iq运算的自适应三相电网电流检测

3.1 ip-iq三相电网谐波检测原理

据三相电路瞬时无功功率理论，通过计算ip、iq即可检测到三相电路谐波电流或无功电流[2]。自适应三相电网电流检测系统如图2所示。该方法中，a相电压ua经过一个锁相环（PLL）和一个正、余弦发生电路得到与它同相位的正弦信号和余弦信号，根据瞬时无功功率理论可计算出ip和iq，ip和iq经自适应LMS滤波系统得到它们的直流分量，从而得到 αβ 坐标系中的基波分量 iαf、iβf；再经过坐标变换得到被检电流 ia、ib、ic的基波分量 iaf、ibf、icf。

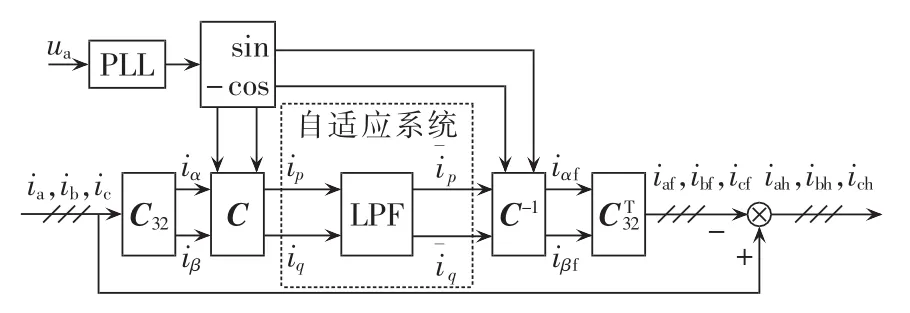
图2 基于ip-iq运算的自适应三相电网电流检测原理Fig.2 Principle of adaptive three-phase grid current detection based on ip-iqmethod

最后将三相负载电流与检测的基波分量相减得到谐波分量 iah、ibh、ich补偿给电网。

3.2 OVS-LMS算法的最佳变步长递推式

一般地，在满足收敛条件的LMS算法中，当离最佳值较远时，要提高算法迭代收敛速度的条件是选择较大的迭代步长，而在偏离最佳值较小时，为保证检测精度减小波动，应该选择较小的迭代步长[13-17]。

考虑对于稳态系统的LMS迭代过程，提出采用最佳变步长的递推公式代替LMS常规算法中的固定步长，即最佳变步长的递推公式的LMS算法（OVSLMS算法）：

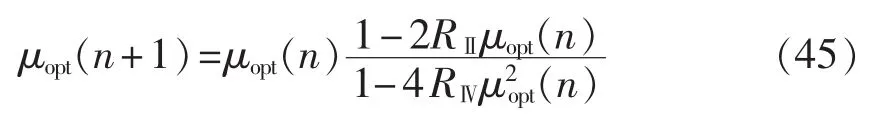
基于ip-iq运算的自适应三相电网电流检测中，根据自适应系统的已知条件，如果令us（n）=K，则RⅡ=E[u2s（n）]=K2，RⅣ=E[u4s（n）]=K4。 其递推关系式为：

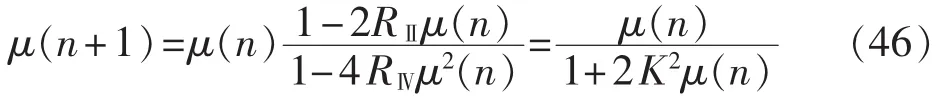
4 仿真实验结果

基于OVS-LMS构成自适应三相电网谐波检测系统如图2所示。在ip、iq的自适应LMS滤波系统中选择迭代步长均满足 0＜μp＜μmax，0＜μq＜μmax。 设从某时刻开始通过前置模拟滤波器滤波后获得的电网三相负载电流如图3所示，含有丰富的谐波分量。电流通过自适应检测系统后，得到直流分量如图4所示；a相基波与谐波电流的检测结果如图5所示；电网三相电流的检测结果如图6所示。可见，新的自适应检测方法可以很好地获取电网基波，实现三相电网谐波电流分量的分离，且其跟踪谐波电流的稳态性能好。

图3 三相负载电流Fig.3 Waveforms of three-phase load current

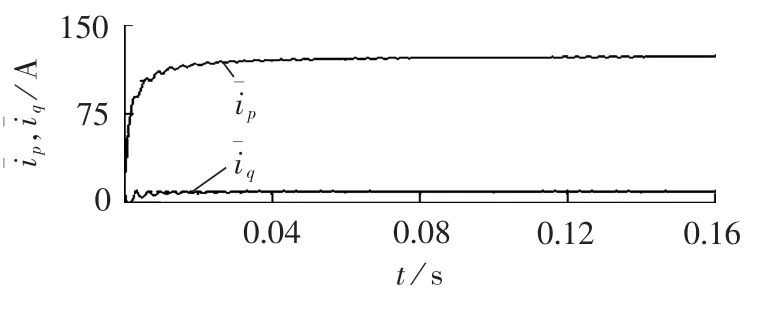
图4 基于OVS-LMS的自适应三相电网电流检测直流分量Fig.4 DC component of adaptive three-phase grid current detection based on OVS-LMS

图5 基于OVS-LMS的自适应三相电网电流检测（a相）Fig.5 Adaptive three-phase grid current detection based on OVS-LMS method（phase a）

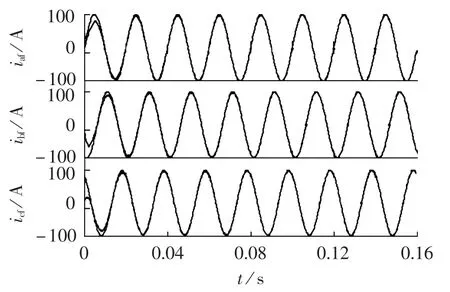
图6 基于OVS-LMS的自适应三相电网电流检测跟随性能Fig.6 Dynamic response of adaptive three-phase grid current detection based on OVS-LMS

上述分析中，变步长算法的初值μ（0）选为0.05。为比较基于LMS变步长算法与常规固定步长算法结果，进行多次仿真实验。为保证较快的响应速度与稳态误差，常规固定步长算法的步长μ取0.01，而变步长算法的初值μ（0）仍确定为0.05。仿真分析如图7和图8所示。

由图8可见，与常规固定步长算法相比，改进变步长LMS算法的收敛速度有所提高。采用常规固定步长LMS算法，检测在2个周期后才趋于稳态；采用变步长LMS算法后，检测在1.5个周期后就已经进入稳态，而且暂态过程效果更好。

图7 基于常规LMS与OVS-LMS的自适应三相电网电流检测权值变化比较Fig.7 Comparison of weights between LMS-based and OVS-LMS-based adaptive three-phase grid current detections

图8 基于常规LMS与OVS-LMS的自适应三相电网电流检测暂态分析（a相）Fig.8 Transient state analysis for LMS-based and OVS-LMS-based adaptive three-phase grid current detections（phase a）

图9为负载电流、基波与检测基波的总谐波畸变率（THD）。可见对于自适应三相电网基波检测而言，采用OVS-LMS算法的THD数值远小于采用常规固定步长LMS算法的THD数值，其稳态性能更好。

图9 基于常规LMS与OVS-LMS的自适应三相电网基波检测的THD比较（a相）Fig.9 Comparison of THD between LMS-based and OVS-LMS-based adaptive three-phase grid current detections（phase a）

5 结论

本文讨论基于LMS的自适应电网电流检测系统快速收敛的步长选择原理，在理论上给出了定量的证明。步长选择原理清楚地表明：在自适应电网电流检测的收敛过程中，偏离最佳解较远时选择较大迭代步长的收敛速度大于选择较小步长的收敛速度。将原理应用于自适应三相电网电流检测系统中，采取基于最优步长选择策略的改进变步长LMS算法，可以加快迭代运算的收敛速度，同时提高稳态的检测精度。