一种改进的基于DCS的分布式多用户协作频谱感知方法*

章坚武，陈晓燕，许晓荣

（杭州电子科技大学通信工程学院 杭州 310018）

1 引言

随着无线通信需求的不断增长，当前固定的频谱分配政策已不能满足人们的需求，因此提出了认知无线电（cognitive radio，CR）技术，从时间和空间上充分利用空闲的频谱资源，从而有效提高频谱资源的利用率[1]。认知节点可以在不影响主用户 （primary user，PU）正常使用的情况下，通过频谱感知检测出当前无线环境中被授权系统的闲置频谱资源，并按照某种机会方式接入空闲频段内进行工作。目前，认知无线电的研究内容[2]包括频谱感知、频谱分析、频谱决策、频谱共享以及频谱移动性管理。其中，频谱感知是CR的最主要任务，是实现频谱管理、频谱共享的前提。

传统的Nyquist采样定理要求信号采样率不小于两倍信号带宽[3]，这显然对相应的硬件设备提出了很高的要求。在认知无线电系统中，为了能够感知到频谱空穴，对认知用户（cognitive user，CU）的终端设备提出了高要求，需要采用高分辨率、高采样率的模数转换器 （analog to digital converter，ADC）[4]、多个模拟前端电路以及高速信号处理器。由此可见，传统的Nyquist采样定理成为宽带认知无线电发展的一大障碍。2004年，Donoho与Candes等人提出了压缩感知（compressed sensing，CS）理论，它指出：如果某长度为N的信号是稀疏的，或在某个变换域上是稀疏的（即信号可以用一组基线性表示，且在该基上仅有K（K≤N）个非零系数），那么就可以将变换所得的高维信号投影到一组测量向量上得到测量值，该测量值维数M远小于信号维数N，从而实现信号由高维到低维的转变，实现这一转变的实质是利用一个与变换基不相关的观测矩阵，最后利用优化求解的方法从少量的投影中以高概率恢复原始信号。在压缩感知的基础上，Baron D等人提出了分布式压缩感知（distributed compress sensing，DCS）理论[5]，该理论建立在信号集合 “联合稀疏模型 （joint sparsity model，JSM）”的基础上，将单信号的压缩采样扩展到信号群的压缩采样，利用信号内部结构和信号间的相关结构实现多个信号的联合重构。

CS理论已深入多个领域，如天文、图像处理、雷达探测[6]等，当然也包括无线通信系统，由于CR系统中频谱信道的占用情况是稀疏的，可以进行基于CS理论的认知无线电宽带压缩频谱感知[7]。目前，国内外对于宽带压缩频谱感知已有较多的研究。参考文献[8]详细介绍了3种单用户频谱感知算法，分别为匹配滤波器检测、能量检测和循环平稳特征检测，并对这3种算法的适用范围、优缺点进行了比较。然而，信号在实际传输过程中会受到多径衰落、阴影效应、噪声不确定等因素的影响，从而制约单用户频谱感知的检测性能。参考文献[9]分析了CS在频谱感知应用中的检测和估计问题，并且给出了检测概率和虚警概率的计算表达式，同时指出多用户协作感知能够克服单用户在认知无线电宽带频谱感知过程中可能出现的检测错误问题。结果表明，多用户参与的频谱协作感知可以提高系统的频谱检测能力，但复杂度则会随着参与协作的认知用户数的增多而上升。

将DCS理论运用于多用户协作频谱感知中，称为分布式压缩频谱感知 （distributed compress spectrum sensing，DCSS），信号的重建算法是DCSS一个至关重要的环节。目前，重构算法主要有凸松弛法和贪婪匹配追踪算法。贪婪匹配追踪算法是目前应用范围广泛的算法，其中的OMP算法则是主流算法之一，OMP算法需要通过迭代计算测量矩阵Φ中所有原子与信号r的内积，找到内积绝对值最大的原子，重建算法的耗时与信号的长度、稀疏度以及认知用户的数量都有着密切的关系[10]。因此在DCSS环境中，当信号长度很长、认知用户数量过多时，信号的重构过程会变长，从而影响频谱感知的实时性。

因此，寻找既能精确地重构出原始信号，又能体现频谱感知实时性的重构算法是DCSS需要考虑的问题。在实际的认知无线网络中，由于频谱的占用情况变化比较缓慢，即当前感知周期起始时刻，主用户占用频谱情况与前一感知周期频谱占用情况相比未发生明显变化，只是主用户的发送功率发生了改变。根据这个实际情况，本文提出了一种改进的基于DCS的多用户协作频谱感知算法，该算法是在OMP重构算法基础上进行的改进，在本文中称为DCS-MOMP（distributed compress sensing-modified orthogonal matching pursuit）算法。该算法的实质是：当前一个感知周期内的频谱占用情况与主用户占用频谱不发生变化或变化缓慢的前提下，利用前一个感知时刻的频谱位置减少重构计算量，从而减小重构时间。

2 系统模型

2.1 压缩感知

压缩感知是一种在对信号进行采样的同时进行压缩的理论，该理论能够从少量的数据信号中提取出原始信息，CS理论的框架如图1所示。

图1 CS理论的框架

由图1可见，CS理论的核心内容可以概括为3部分：信号的稀疏表示、观测矩阵的设计和重构算法的设计。

假设离散实值信号X的长度为N，X可以是稀疏的，也可以用一组正交基矩阵 ΨT=[ψ1,ψ2,ψN]线性表示（ΨT表示Ψ的转置），则有：

其中，鄣是 N×1矩阵，Ψ 是 N×N 矩阵，若系数集合{αi}中仅有K（K≤N）个非零（或远大于0）的系数，则Ψ为信号X的稀疏基或称X是K稀疏的。

在测量过程中，将信号X投影到一组测量矩阵Φ上，得到测量值Y，从而实现了信号从高维到低维的转换，矩阵表达式为：

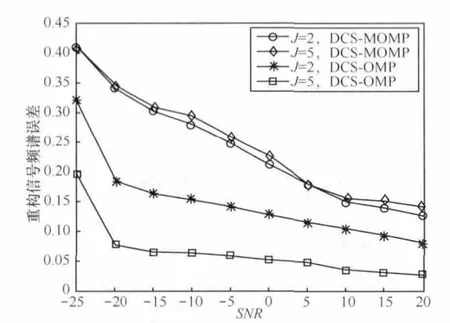
其中，X是N×1矩阵，y=[y1,y2,ym]T是M×1观测向量，其元素为 ym=；Φ=[φ1,φ2,…,φm]是一个 M×N（M≤N）测量矩阵，Θ=ΦΨ是压缩感知矩阵。由于测量值维数M远小于信号维数N，要从低维信号中恢复出高维信号是一个NP难问题，但鄣是K稀疏的，即仅有K个非零系数，且K

RIP准则的一个等价约束是：要求测量矩阵Φ与稀疏矩阵Ψ不相关。

当式（2）中的矩阵Φ满足RIP准则，即满足式（3）所要求的不等式时，CS理论就能从式（2）中求解出稀疏系数，再代入式（1）中恢复出原始信号，解码的最直接方法就是利用l0范数求解式（2）：

由于求解式（4）是一个NP难问题，需要转化为l1范数凸优化问题才能求解，即：

典型的最小l1范数凸优化重构算法有BP（凸松弛）法、GPSR（贪婪匹配追踪）算法等。由于凸松弛法具有计算复杂度高的缺点，贪婪匹配追踪算法逐渐成为重构算法的主流，如OMP、CoSaMP等算法都是典型的贪婪匹配追踪算法。

2.2 分布式压缩频谱感知

在CS理论的基础上，Baron D等人提出了DCS理论，建立在信号集合JSM[11]的基础上，该联合稀疏模型可以分为两种，分别为 JSM-1、JSM-2。

假设一个信号群有 J个信号，用 Xj，j=1，2，…，J表示，这些信号在同一个稀疏基Ψ下是稀疏的，但不同信号的观测矩阵Φ互不相同，如信号Xj所对应的观测矩阵为Φj。

（1）JSM-1

在JSM-1中，每个信号由两部分组成，分别为信号的公共部分和特有部分，表示为：

其中，Zc表示信号的公共部分，即各个信号相同的分量，在同一个稀疏基下有相同的稀疏度K，如式 （7）所示；Zj表示信号的特有部分，即各个信号所特有的分量，在稀疏基下的稀疏度是不同的，如式（8）所示。因此，在JSM-1中，信号群拥有相同的稀疏基，但在该稀疏基下的稀疏度是不同的，为K+Kj。

（2）JSM-2

在JSM-2中，信号群中的每个信号只有公共部分，即在同一个稀疏基Ψ下的稀疏度都为K，只是系数aj不同，表示为：

JSM-2的一个典型应用场景是认知无线电宽带频谱感知。在认知无线网络中，处于空间上不同位置的认知用户同时感知主用户发射的信号，由于感知信号传输路径不同，这些信号的衰减和相移均不相同，但它们的稀疏度是一致的。另外，JSM-2的一个有效应用是MIMO系统。

本文通过引入JSM-2，提出了基于DCS的多用户协作频谱感知方法，其特点为：利用空间的宏集合弥补了单用户在频谱感知过程中由信号传输时的多径衰落、阴影效应、噪声不确定等因素引起的检测错误问题，并且要求各认知用户不必对压缩采样信号进行重构，而是直接将压缩采样数据发送给控制中心，由控制中心对数据进行联合重构，进而做出全局判决，这大大降低了各认知用户在频谱感知过程中压缩采样、信号重构、局部判决所带来的功耗与时延问题。基于DCS的多用户协作频谱感知原理如图2所示。

图2 基于DCS的多用户协作频谱感知原理

假设认知无线电网络中进行频谱感知的认知用户数为 J，第i个认知用户感知到的信号为 xi，其长度为N，yi是长度为 M的测量向量，Ψi是稀疏基，Φi是观测矩阵，i=1，2，…，J。基于 DCS的多用户协作频谱感知算法步骤如下。

（1）主用户发射信号，各次用户对所感知的信号xi根据式（1）、式（2）进行压缩采样，得到各自的测量向量yi，i=1，2，…，J。

（2）各认知用户直接将采样数据yi发送给控制中心。

（3）控制中心根据DCS重构算法对所接收到的采样数据集合Y={y1，y2，…,yJ}进行联合重构，得到联合重构信号集合 X={x1，x2，…,xJ}。

（4）利用能量检测方法进行频谱感知，最终得到全局判决结果。

该算法可以精确地恢复出原始的信号，并且从上述算法的步骤（3）中可以看出，重构算法是DCSS算法的关键步骤，也是复杂度最高的步骤。在实际的认知无线网络中，由于频谱的占用情况变化比较缓慢，而且大多数情况下连续若干时间内频谱占用情况不发生改变，利用这个实际情况，对OMP算法进行改进，把上一感知时刻的频谱占用情况作为先验条件，从而可以大大减小重构复杂度，特别适合于多用户协作频谱感知环境。

3 MOMP分布式协作重构算法

3.1 算法理论

本文提出的DCS-MOMP算法的基本思想是：在当前感知周期起始时刻，主用户所占用频谱情况与前一感知周期频谱占用情况相比没有发生变化的情况下，利用相邻感知时刻频谱占用情况不变的假设，将采用MOMP进行重构的信号与原信号进行比较，得出重构信号误差，用于判断频谱占用情况是否改变，若在误差门限范围内，则认为信道占用情况未改变，运用DCS-MOMP算法，否则利用DCS-OMP算法对信号进行重构。该算法用于多用户协作频谱感知中，不仅可以精确地恢复原始信号，还可以减小信号重构时的计算量，从而减少计算复杂度，提高频谱感知的实时性。

3.2 算法具体步骤

假设上一感知时刻的频谱占用情况已知，用b表示一个长度为C的0-1序列，C为信道个数，0表示信道未被占用，1表示信道被占用，b（c）表示第 c个信道的占用情况c=1，2，…，C，J个认知用户同时进行频谱感知。

输入：稀疏基Ψ，观测矩阵Φj，第j个认知用户的压缩采样矩阵 Θj=ΦjΨj，测量向量 yj，稀疏度 K。

通过式（10）确定最大值所对应的角标pos。

（2）利用式（11）更新索引集：

同时把压缩采样矩阵的第pos列置0，即Θpos=0。

（3）更新支撑集，记录角标pos的位置：

（4）根据最小二乘法计算频域稀疏向量，其中（）+表示伪逆运算，a|Ω表示a中由Ω内元素指定的位置上的元素：

（5）更新残差：

（6）若|Λ_itj|≥K，其中|·|表示集合中元素的个数，则迭代停止，进入下一步；否则，l=l+1，回到步骤（1）。

（7）计算重构信号：

（8）计算重构信号误差：

如果e小于给定的误差门限值ε，则说明上一时刻频谱占用情况与当前时刻相同，可以利用DCS-MOMP算法达到重构效果，同时减少重构复杂度；反之，则说明频谱信道占用情况发生改变，则采用DCS-OMP算法。

3.3 算法计算复杂度

上述算法中，寻找最大值角标位置是基于前一感知时刻的频点位置，因此可以减小频谱位置的搜索范围，从而减小重构计算复杂度。

假设信号的采样点数为N，压缩采样点数为M(M<

而DCS-MOMP算法利用了前一次感知时刻的频谱占用情况，每次迭代只需在K个频点上计算。在DCS-MOMP算法中，外层循环次数仍然为K，但在第（1）步中只是在上一感知时刻频点上进行运算，即每个认知用户的Θj的给定列（上一感知时刻频点的位置）与第i-1(1≤i≤K)次迭代的残差相乘，因此DCS-MOMP算法在第（1）步中的计算复杂度为 2M×N×K×J次乘法、M×K×K×J次加法、2M×K×K×J次复乘运算。

因此，对两种算法的复杂度进行比较可知，DCS-MOMP计算量分别减少了 2M×(N-K)×K×J次乘法、M×(N-K)×K×J次加法、2M×(N-K)×K×J次复乘运算，明显减少了计算复杂度，从而大大减少了系统能耗。

4 仿真与结果分析

假设信道为高斯白噪声，目标总带宽为100 MHz，等分为C=50个信道，采样点数为N=500，则每个子带的采样点数为W=N/C=10。设前一时刻被占用的子带数为I=2，则稀疏度为I×W=20，设T和T+1时刻为相邻的感知时刻。在T时刻，信噪比SNR=10 dB、认知用户数J=2、压缩比为M/N=0.2时，信号的功率谱、频谱以及信道的占用情况如图3所示。在T+1时刻，DCS-OMP和DCS-MOMP算法对信号进行重构所得到的重构频谱和感知信道的占用情况分别如图4、图5所示。

图3 在T时刻，信号的功率谱、频谱与信道占用情况（J=2，SNR=10 dB，M/N=0.2）

图4 在T+1时刻，DCS-OMP算法重构的信号频谱与信道占用情况（J=2，SNR=10 dB，M/N=0.2）

图5 在T+1时刻，DCS-MOMP算法重构的信号频谱与信道占用情况（J=2，SNR=10 dB，M/N=0.2）

如图5所示，T时刻和T+1时刻为两个相邻感知时刻，两个时刻信道占用情况没有发生改变。比较图4和图5可以看出，在T+1时刻，DCS-OMP和DCS-MOMP均可以精确地重构出信号，得到正确的信道占用情况，运用DCS-OMP算法所得的重构频谱误差为0.112 582，运用DCS-MOMP算法所得的重构频谱误差为0.129 502；运用DCS-OMP算法进行重构的耗时为7.542 s，而运用DCS-MOMP算法进行重构的耗时为5.451 s。因此，当信噪比SNR=10 dB、认知用户J=2、压缩比M/N=0.2时，运用DCS-MOMP算法进行重构的耗时较DCS-OMP算法少，这是因为改进算法只是在上一时刻的感知频点上进行信号重构，节省了在整个频谱范围内寻找最大值所对应的频点位置所需的大量计算。

为了能够充分显示DCS-MOMP算法重构节约计算量的特点，本文将DCS-OMP和DCS-MOMP算法的重构耗时进行了比较。信号长度N=1 000、信噪比SNR=20时，稀疏度与耗时的关系如图6所示，对于不同认知用户数（J=2、J=5）进行了100次（蒙特卡洛）仿真。

图6 对于认知用户数与不同稀疏度时的耗时比较

由图6可知，在不同认知用户数（J=2、J=5）下，随着稀疏度K的增大，两种算法的耗时也随之增大。当稀疏度较小时，DCS-MOMP算法耗时要小于DCS-OMP算法，且当认知用户较多（J=5）时，两种算法的重构耗时差距更为明显。但随着稀疏度的逐渐增大，两种算法的耗时差距逐渐变小。因此，当信号稀疏度较小且认知用户数较多时，DCS-MOMP算法优势明显。

当信噪比SNR=20、稀疏度K=40时，信号长度与耗时之间的关系如图7所示。对不同认知用户数（J=2、J=5）进行了100次（蒙特卡洛）仿真。

图7 不同认知用户数与不同信号长度时的耗时比较

由图7可知，在认知用户数不同时，随着信号长度的增大，两种算法耗时均增大，DCS-MOMP算法增长幅度较为缓慢，DCS-OMP上升幅度则较大，且在认知用户数为5时，两种算法的耗时差距更为明显。即在信号稀疏度较小且协作用户数较多的情况下，DCS-MOMP算法优势明显。

当信号长度N=500、稀疏度K=20时，不同信噪比与重构信号频谱误差之间的关系如图8所示。针对不同认知用户数（J=2、J=5）进行了 100 次（蒙特卡洛）仿真。

由图8可知，随着信噪比的增大，两种算法的重构信号频谱误差均逐渐减小，但在相同的信噪比下，DCS-MOMP算法的重构信号频谱误差高于DCS-OMP算法，但随着信噪比的增大，误差的差异逐渐减小。即DCS-MOMP算法重构误差较DCS-OMP重构误差大，但在信噪比较高的情况下，误差不断趋近于DCS-OMP算法，这是因为在多用户协作频谱感知环境中，DCS-MOMP算法以增大重构误差为代价减小重构复杂度。

图8 不同认知用户数与不同信噪比下重构信号频谱误差比较

根据以上性能分析可知，本文提出的DCS-MOMP算法适用于在噪声影响较小的多用户协作认知无线网络环境中（即认知用户数J较多的场景中）。

5 结束语

多用户协作频谱感知技术利用空间的宏集合弥补了单用户频谱感知过程中的检测错误问题，但在信号重构过程中增加了计算量。在实际的认知无线电系统中，频谱占用情况变化缓慢，即当前感知时刻频谱占用情况和上一感知时刻频谱占用情况基本一致。本文以此为前提，提出了一种改进的基于DCS的DCS-MOMP，该方法利用上一感知时刻的频点，大大减小了在确定最大值所对应的频谱位置时的计算量。仿真结果表明，DCS-MOMP算法更适用于多用户协作认知无线网络场景中，不仅可以得到与原DCS-OMP算法相同的重构性能，而且明显减小了重构复杂度。

1 Haykin S. Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Area in Communication,2005,23(2):201～220

2 闫琦.认知无线电频谱感知若干关键技术研究.西安电子科技大学硕士学位论文,2011

3 顾彬,杨震,胡海峰.基于压缩感知信道能量观测的协作频谱感知算法.电子信息学报,2012,34(1):14～19

4 赵知劲,张鹏,王海泉等.基于OMP算法的宽带频谱感知.信号处理,2012,28(5):725～728

5 Baron D,Wakin M B,Duarte M F.Distributed compressed sensing of jointly sparse signals.Proceedings of IEEE 39th Asilomar Conference on Signals,Systems and Computers,Pacific Grove,CA,USA,2005:1537～1541

6 Herman M,Strohmer T.High-resolution radar via compressed sensing.IEEE Transactions on Signal Processing,2009,57(6):2275～2284

7 石磊,周正,唐亮.认知无线电网络中的压缩协作频谱感知.北京邮电大学学报,2011,34(5):76～79

8 Wang C L,Chen H W,Chou Y R.A credibility-based cooperative spectrum sensing technique for cognitive radio systems.Proceedings of Vehicular Technology Conference(VTC Spring),2011 IEEE 73rd,Budapest,Hungary,2011:1～5

9 Gu B,Yang Z,Hu H F,et al.Cooperative compressed sensing forwide-band spectrum detection.Proceedingsofthe6th International Conference on Wireless Communications Networking and Mobile Computing(WiCOM),Chengdu,China,2010:1～4

10 吴尘.基于压缩感知的信号重构算法研究.东南大学硕士学位论文,2012

11 Baron D,Duarte M F,Wakin M B.Distributed Compressive Sensing.Cornell University Library,2009