微机械谐振子单端口电容检测方法研究
2013-09-28邢维巍谷姗姗王炜明章建军樊尚春
邢维巍,谷姗姗,王炜明,章建军,樊尚春,3
(1.北京航空航天大学仪器科学与光电工程学院,北京 100191;2.北京航空工程技术研究中心,北京 100076;3.惯性技术国防科技重点实验室,北京 100191)
0 引言
谐振式微传感器是基于谐振测量原理的传感器,当被测量作用到传感器上,会引起敏感元件谐振频率的变化,通过测量谐振频率的变化值,可以得到被测量的值[1]。谐振式传感器的输出量是反映外部物理量变化的频率量。因此,必须给梁一定的扰动力,使梁发生谐振,即激振。同时,还必须通过特定的方式测量梁的振动频率,即拾振。激振、拾振的好坏关系到谐振器的性能,解决谐振子的激励与检测问题至关重要。
在常见的激励/检测技术中,静电激励/电容检测方式具有体积小、非接触、响应快、功耗低、与IC工艺兼容、集成度高等优点[2],在提高谐振式微谐振子的测量精度、灵敏度、响应速度及降低功耗方面有着很大的优越性,在微机械谐振式陀螺、加速度计、压力传感器及湿度传感器等中也得到不同程度的应用,但该方法由于激励与检测电路间的串扰受到一定的限制。目前,解决串扰的方法大致分为两类:第一类采用激励与检测使用两个电极,即双端口式[3];第二类则采用激励与检测共用一个电极,即单端口式[4]。实际应用中大多采用双端口静电激励/电容检测,但在同频激励的双端口谐振子中,激励、检测信号易耦合产生同频干扰,增加了信号检测的难度,严重的情况下将无法观测到谐振现象。基于频域分离的单端口静电激励/电容检测简化了结构,并通过测量被测电容的电流信号的三次谐波,使得检测信号与激励信号在频域上分离[5],可有效地解决双端口谐振子同频激励的耦合干扰问题。
1 理论基础
利用静电力的倍频效应产生频率为激励频率两倍的激励力,最终产生频率为激励频率三倍的电流输出信号[2],使得激励频率、振动频率和检测信号频率在频域上分离,采用同一电极进行激励和检测时,可避免干扰问题。此法称为THM(Third Harmonic Method)法[5]。
静电激励/电容检测一般采用平行板电容或梳齿元件。平行板电容结构工艺简单,一般为垂直驱动,驱动力较大,但驱动力与极板间的距离呈非线性关系,从而限制了可动结构的位移[6]。文献 [7]给出了一种基于平行板电容的谐振器,如图1所示。电容的一个电极由谐振子的全部或部分面积构成 (动极板),另一个电极由一个靠近谐振子的表面构成 (静极板)[6]。

图1 一种基于平行板电容的谐振子
1.1 THM法
利用纯交流电压激励谐振子时,设激励信号为

式中:V0代表激励电压幅值。
将谐振梁等效成质量-弹簧-阻尼器系统[2],则梁的稳态振动位移可表示为
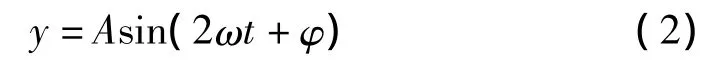
式中:A是梁的振动幅值;φ是在ω处的相位。
谐振子的振荡使得相对静电极产生了随振荡位移相应变化的电容,电容值

式中:ε0和εr是谐振子的介电常数和自由空间的介电常数;b和l是平板电容器的长和宽;d是平板电容器极板间距。
又Q(t)=C(t)·v(t),故而
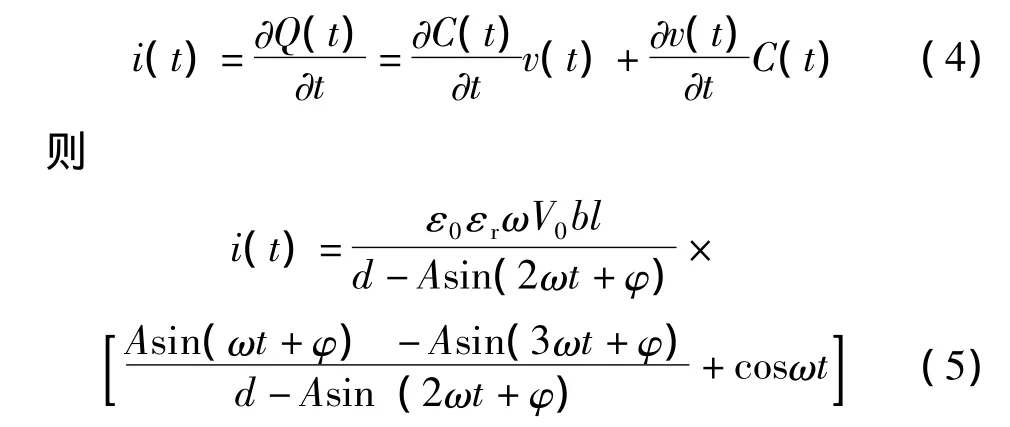
由式 (5)可知,电容的输出电流包括ω和3ω两种频率成分,其中3ω电流信号用来检测谐振器的振动,可表示为
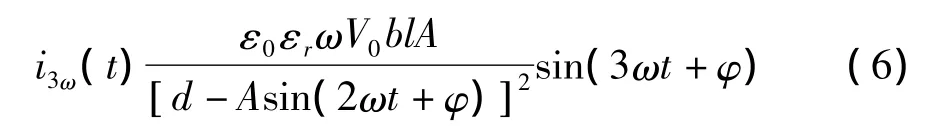
当A<<d时,

式中:C0是电容器初始电容。
考虑到寄生电容Cp的影响,则输出电流
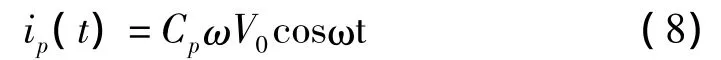
由式 (7),(8)可知,电容器输出电流的三次谐波幅度与谐振子振动幅度成正比;电容器输出电流的三次谐波与谐振子振动位移同相位;在三倍频率处,无其他信号干扰检测信号,可实现激励与检测信号的频域分离。
1.2 隔离变压器的选择
由于本实验被测对象是微弱电容信号,需要重点考虑变压器的谐波特性。表1给出了现在市场上主要的几种牌号的非晶、超微晶合金的性能。
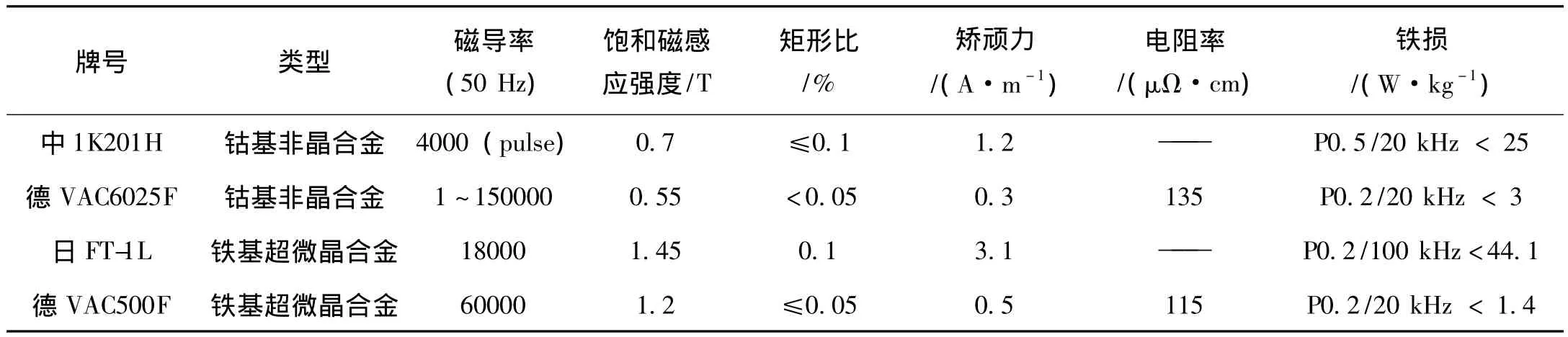
表1 不同牌号的非晶、超微晶合金性能比较
表1中,德国的VAC500F铁基超微晶合金在磁导率、饱和磁感应强度、矩形比以及铁损等方面具有一定的优势,综合性能优异,故选用该合金作为隔离变压器的磁芯材料。为尽量降低变压器漏磁对信号检测的影响,选用闭合磁芯。环形磁芯与矩形磁芯相比,磁场分布更均匀,效率更高。另外,磁芯材料内部的应力对磁性能影响较大,非晶、超微晶合金在加工过程中对应力敏感性高,而环形磁芯产生的加工应力较小,因此其磁性能也相对较优。综合考虑,本文选用德国的VAC500F铁基超微晶合金的环形磁芯制作隔离变压器。
2 系统设计
基于THM法及隔离变压器技术,设计了单端口静电激励/电容检测方案,该测试系统总体框图如图2所示。

图2 单端口静电激励-电容检测系统的总体框图
激励信号源产生一定频率和幅值的电压信号,使谐振子起振并维持谐振状态。为满足微传感子对信号源同步性的要求,本文采用一种对数字频率信号进行同步输出的方案[8],其原理框图见图3。使用AD9852提供准确的数字频率输出信号作为FPGA的输入,由FPGA实现对信号的N次分频及同步输出。实验表明,在1 Hz~10 MHz的输入频率下,同步输出信号的频率偏差小于 0.01 μs。
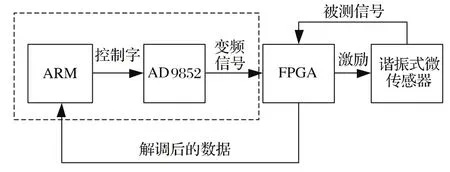
图3 谐振式微传感器专用同步信号源框图
激励信号源输出阻抗较高,而作为后级的隔离变压器的输入阻抗往往较低,缓冲级起着承上启下的作用,它实现较高的输入阻抗和较低的输出阻抗,完成前后级的阻抗匹配。
隔离变压器在系统中实现激励电压幅值放大、提供反相激励电压以及抑制低频噪声的作用。
由电流谐波分析[9]知,一次电流谐波比三次电流谐波高大约一个数量级,为避免将三次谐波放大到采样的范围时,一次谐波已使放大器饱和或超出最大采样范围,本文采用对补偿电容施加激励电压信号的等值反向电压信号的方案,采用对容值接近谐振子静态电容的补偿电容施加激励电压的反向电压,其输出电流与谐振器的输出电流在OPA827的反向端进行叠加,抵消大部分一次谐波[2]。
为防止C/V转换的输出信号含有的大量高次谐波造成信号混叠,采用LPF滤除部分高频成分以使采样系统满足采样定理,LPF电路兼具有幅值放大作用。信号采集装置用于采集被测模拟电压信号,并将其转换为数字信号送往FPGA进行数字解调。
3 实验验证
3.1 实验结果
谐振器与激励检测电路的连接方式见图4。由于谐振器加工时为引出接线端,为对其进行激励检测,利用探针来输入激励信号、输出检测电流。

图4 谐振器与激励检测电路的连接方式
实验关键在于确定谐振子的起振电压与谐振频率,采取试探法。取激励信号频率50 kHz,调节激励信号源输出电压幅值,同时从小到大调节激励信号频率,在0.65 V左右观测到谐振子起振。固定该激励电压幅值,在0~100 kHz范围内进行扫频,找到两个谐振频率点,实验现象如图5,6所示 (图中,频率单位:Hz,电压功率谱单位:
图5中实验现象是激励信号频率在9.091 kHz附近的频率范围内调节时谐振子输出电流的三次谐波幅值变化情况。图6是激励信号频率分别为9.0,9.091,9.2 kHz时谐振子输出电流三次谐波的局部频谱。通过对图5,6的观察比较初步判断,当激励信号频率为9.091 kHz时,三次谐波的幅值达到最高,谐振梁处于谐振状态。
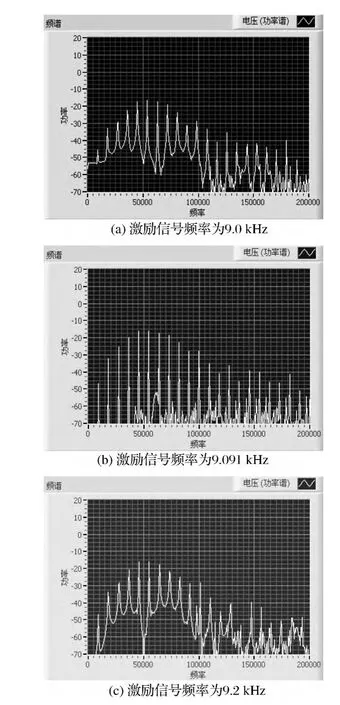
图5 激励频率在9.091kHz附近变动时输出信号频谱
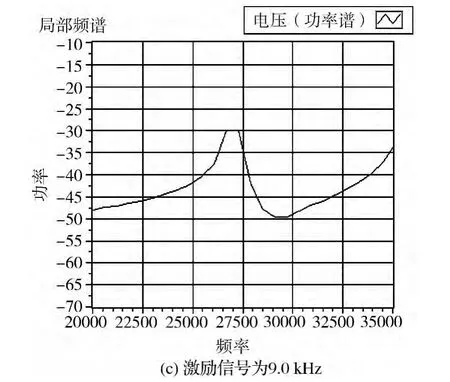

图6 激励频率在9.091 kHz附近输出电流三次谐波局部频谱
同法,当激励信号在55.757 kHz附近调节时,谐振梁也处于谐振状态。激励信号频率为55.7,55.757,55.8 kHz时的实验现象和输出电流三次谐波局部频谱图分别如图7,8所示 (图中,频率单位:Hz,电压功率谱单位:
在0~100 kHz频率范围内调节激励信号频率,共找到两个谐振频率值,分别是9.091 kHz和 55.75 kHz。初步判断这两个频率值分别为谐振梁的一阶振动模态和二阶振动模态的固有频率。
3.2 实验分析
为验证上述判断的正确性,可作如下分析。
假使被测谐振梁为欧拉-伯努利梁,这时谐振梁的频率方程[10]可表达为
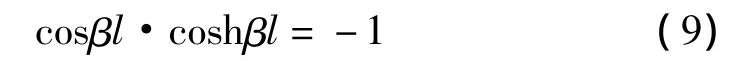
方程的前两个根为β1l=1.875,β2l=4.694,悬谐振梁的固有频率为
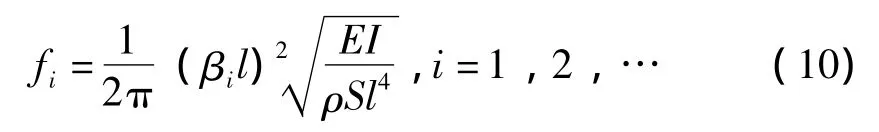
式中:E为谐振梁材料的弹性模量,Pa;I为谐振梁的截面惯性矩,m4;ρ为谐振梁材料的密度,kg/m3;S为谐振梁横梁的横截面积,m2;l为谐振梁的有效长度,m。
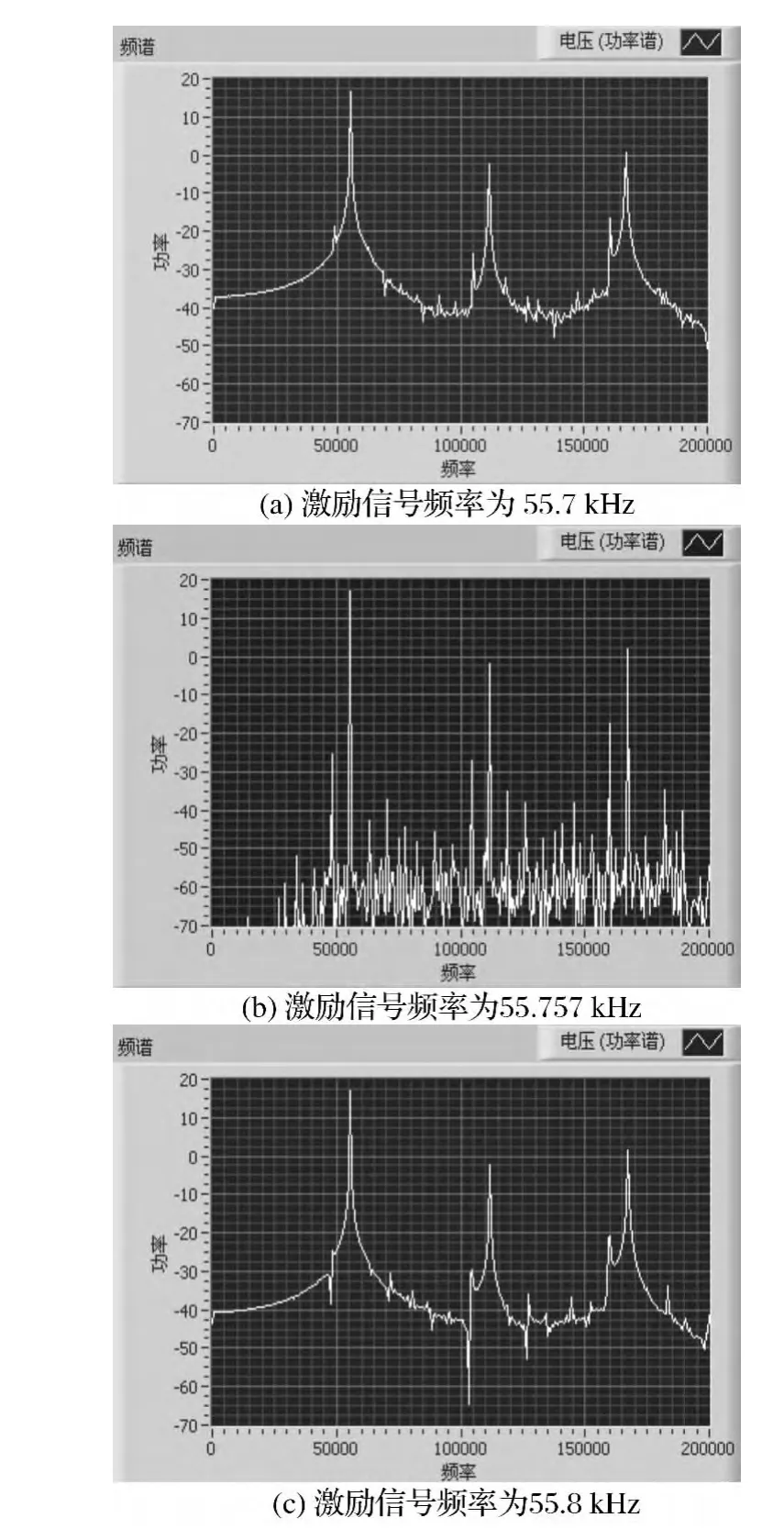
图7 激励信号频率在55.757 kHz附近变动时输出信号频谱
谐振梁横梁的横截面为矩形,其横梁截面惯性矩为

其横梁横截面积为

式中:b为梁的宽度,m;h为梁的厚度,m。将(11),(12)代入 (10),谐振梁第i阶振动模态的固有频率可写为
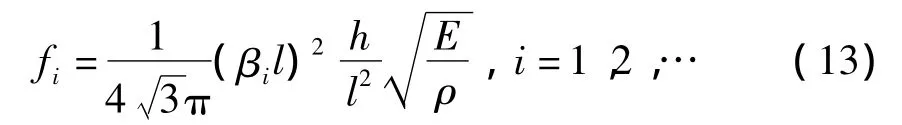
于是,谐振梁的一阶振动模态固有频率
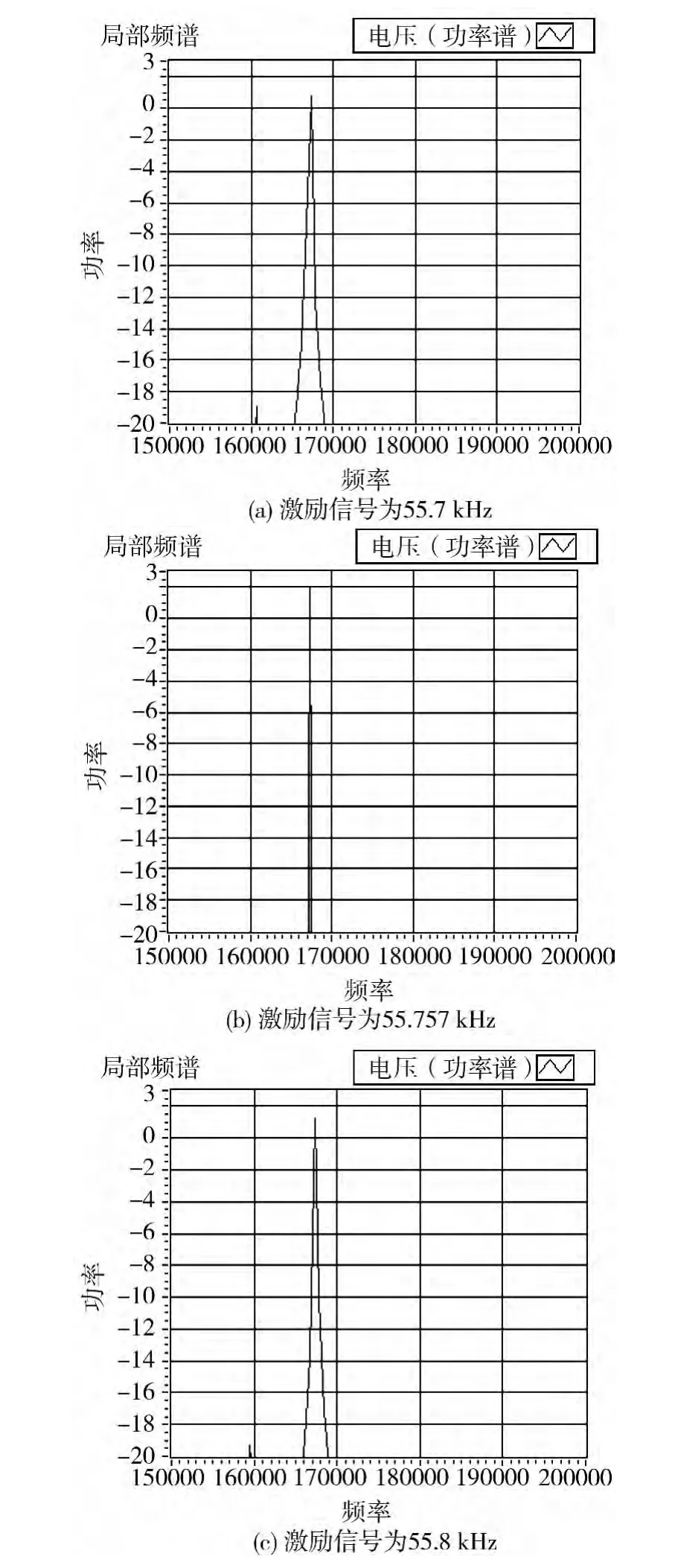
图8 激励频率在55.757 kHz附近输出电流三次谐波局部频谱

在式 (14)和 (15)中谐振梁各项参数已知的情况下 (见表2),可以根据任一阶振动模态的固有频率反解出谐振梁的厚度。若由各阶模态固有频率计算出的梁厚度相等,则说明,初步判定的谐振频率值确是谐振梁的固有频率。

表2 谐振器的主要参数
经计算,由谐振梁第一阶振动模态固有频率求出的梁厚度h(1)=0.882 mm,由谐振梁第二阶振动模态固有频率求出的梁厚度h(2)=0.866 mm。考虑误差因素的前提下,验证了本文设计方案的正确性。
4 结论
本文提出了一种基于频域分离法的单端口静电激励-电容检测方案。采用全硬件电路设计实现谐振子的激励、检测与数字解调,达到与NI系统进行采集、处理相仿的结果,实验结果表明,该硬件测试系统可以有效地检测出微机械电容式传感器的振动信息,为下一步实现单端口谐振器的闭环打下了基础。方案中谐振器的信号引出端采用探针的设计提高了检测的可靠性。
[1]邢维巍,张晓灿,樊尚春,等.微机械谐振器的快速测试方法[J].传感技术学报,2012,25(2):198-201.
[2]樊尚春,陈晨,邢维巍.微谐振器的单端口静电激励-电容检测方法研究 [J].传感器与微系统,2012(7):36-38,41.
[3]Linder C,Zimmermann E ,NF De Rooij.Capacitive polysilicon resonator with MOS detection circuit[J].Sensors and Actuators A:Physical,1991,27(1-3):591-595.
[4]Putty M W,Chang S C,Howe R T,et al.One-port active polysilicon resonant microstructures[C]//Proc.IEEE Micro E-lectro Mechanical Systems,Workshop.Salt Lake City:IEEE,1989:60-65.
[5]Farzan Alavian Ghavanini,Henrik Rödjegärd,Peter Enoksson.An easy-to-implement method for evaluation of capacitive resonant sensors[J].J.Micromech.Microeng.,2006,16:156-160.
[6]邢维巍,彭振江,樊尚春.硅微谐振式压力传感器中的单端口静电激励 -电容检测方法研究 [J].计测技术,2012,32(S1):35-38.
[7]IJntema D J,Tilmans H A C.Static and dynamic aspects of an air-gap capacitor[J].Sensors and Actuators A,1992,35:121-128.
[8]邢维巍,王炜明,谷姗姗,等.谐振式微传感器同步专用信号源设计 [J].计测技术,2013,33(5):29-32.
[9]樊尚春,陈晨,邢维巍.单端口静电激励/电容检测谐振器的谐波分析 [J].振动、测试与诊断,2013,33(4):653-659.
[10]刘习军,贾启芬.工程振动理论与测试技术[M].北京:高等教育出版社,2004.
