采用MathCAD设计异形导体压辊参数
2013-09-28赵凯斌任金玲赵行斌孙建卫
赵凯斌, 任金玲, 赵行斌, 林 磊, 孙建卫
(1.江苏亨通电力电缆有限公司,江苏苏州215234;2.哈尔滨工程大学,黑龙江哈尔滨150001)
0 引言
在电力电缆制造行业中,低压电缆为了节约原材料、缩小电缆外径、降低电缆制造成本,技术人员设计出了紧压扇形导体、紧压瓦形导体等异形导体结构。但异形导体结构设计及计算相对较复杂,如何准确并快速计算出异形导体结构参数成为重中之重。针对该问题,出现了多种不同的计算方法,如:近似设计计算法、CAD设计法、计算机程序语言设计法、Excel函数宏表计算法等[1]。以上方法都是行之有效的,可以满足实际工程设计的需要,但在电缆行业中,大多数技术人员对以上方法的应用存在一定的困难。
为满足广大电缆工程技术人员的需要,本文提出了一种新的异形导体压辊计算方法和计算实例,即用MathCAD的函数计算功能快速设计异形导体压辊尺寸。
1 扇形导体压辊参数设计
1.1 几何模型图
根据几何知识,可将扇形压辊轮廓做以下划分(见图1)。
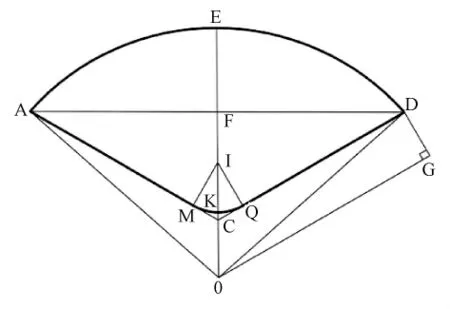
图1 扇形压辊几何模型图
1.2 扇形导体压辊参数计算过程
一般设计扇形导体是通过反算,先根据铜材电阻率、导体紧压程度计算出导体的轮廓截面,以此设计扇形压辊,此处压辊轮廓面积计算不作介绍,具体方法见文献[2]。
已知扇形导体标称截面为S0,压辊轮廓截面积为 S,导体绝缘厚度为 δ,∠ACD为120°,设∠AOE为α,扇形半径为R,扇形轮廓底弧圆角半径为r。
结合图1所示,依据几何知识可得:
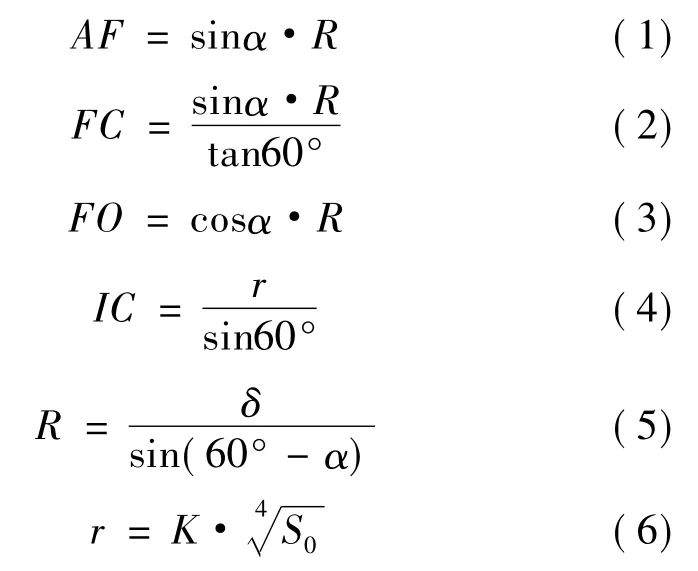
式(6)中,K为与导体几何形状及电压等级有关的经验系数,三芯电缆取0.64。
压辊轮廓截面积:
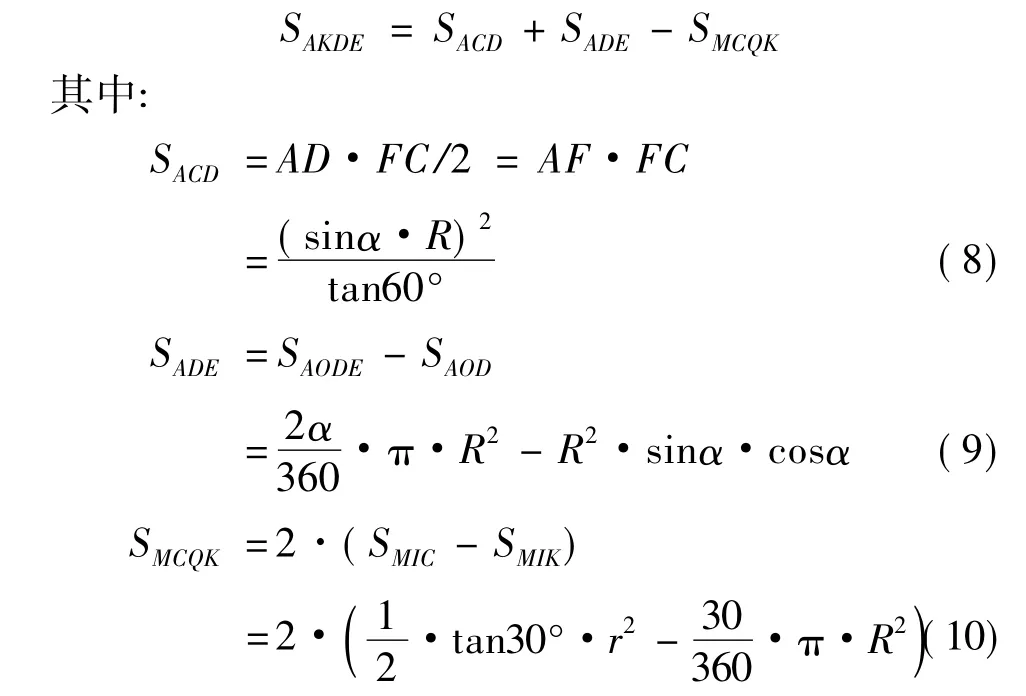
将式(8)(9)(10)带入式(7)中得:
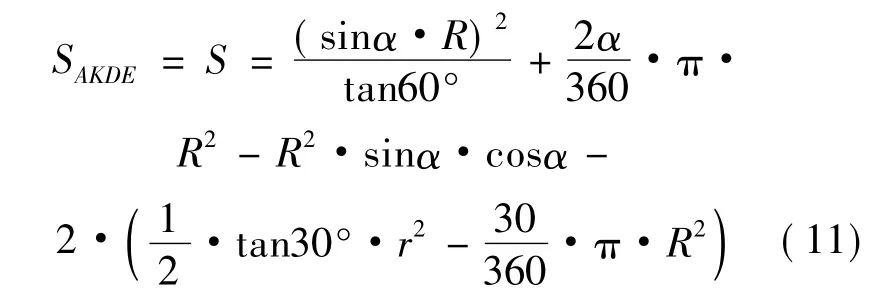
将式(11)化简(角度转化弧度)得:
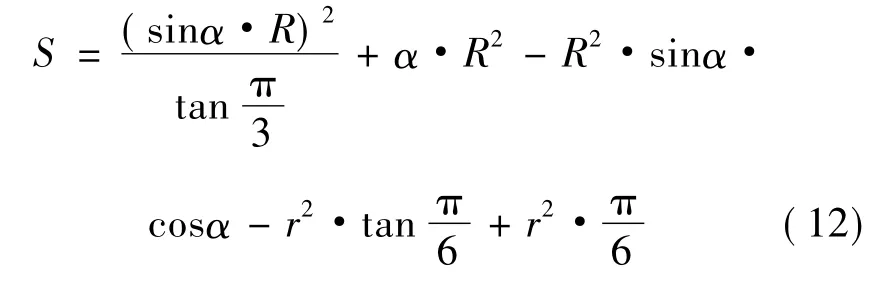
将式(5)(角度转化为弧度)代入式(12)中得:
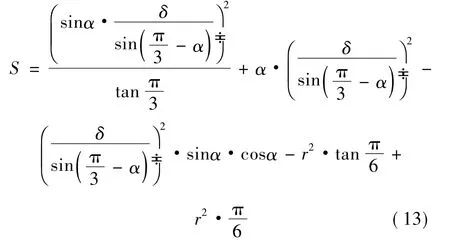
式(13)中δ、S为已知,r由式(6)可求得,故此式是关于α的一元多次方程,用MathCAD可以求出α的值。
若已知 α 的值,即可求出 R、AF、FC、FO、IC 等相应参数,根据以上参数就可确定扇形压辊的相关尺寸。
2 MathCAD计算实例
2.1 MathCAD 简介
在MathCAD中,存在三个区,即数学区、文本区、图像区。数学区是专门为书写数学表达式或其同类内容(如程序)而设计的一种对象。虽然它也能接受字符(英文、中文、希腊文),但并不当做普通意义下的文词符号,而总是把它们当做数学变量名或函数名来理解,是作为数学表达式的组成部分来接受并处理的。
MathCAD系统提供了几个专门用于求函数和多项式根的内部函数,用它们可以方便地求出方程的根。在MathCAD系统内部,root函数是根据数学中求根的割线法(Secant Method)编程而成的内置函数。根据割线法的原理,在使用此函数求根之前,先给未知数x赋予一个初始值,这个值是猜测方程根的可能位置来指定的,系统将这个值作为数值逼近的起点,通过多次分割迭代求出方程的根。
2.2 计算实例
以导体角度为120°的扇形50 mm2导体为例,将以上相关数值及关系式输入MathCAD中(见图2),输入所有的参数及公式后,即可求得相应的压辊尺寸,若截面积变化,只需变换已知参数,即可求得不同截面积的压辊尺寸。
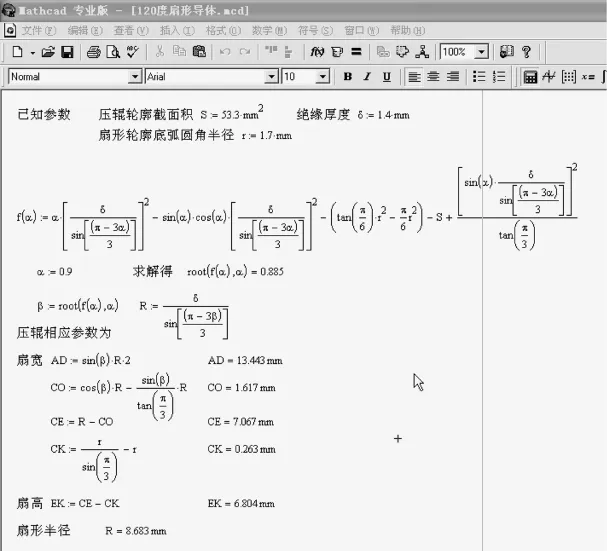
图2 MathCAD计算实例
3 结束语
实践证明,采用此种方法设计扇形导体压辊简单易行,设计出的压辊尺寸准确性高,可大大提高技术人员的工作效率。
此种方法同样适用于其他电力电缆异形导体压辊设计,我们已成功应用于三芯、四芯扇形导体压辊设计,紧压出的扇形导体结构尺寸与实际生产中所测数据基本一致。
[1]李章学.设计异形导体压辊参数的一种新方法[C]//电线电缆技术专题.2010.56-59.
[2]周俊民,蒋炜华,王松显,等.紧压扇形导体压辊空型的最佳设计方案[J].电线电缆,2010(4):39-42.
[3]钱 伟,吕锁成.电力电缆分层紧压扇形导体紧压轮的设计[J].电线电缆,1999(4):31-34.
[4]王春江.电线电缆手册(第一册)[M].北京:机械工业出版社,2008.
[5]张晓丹,李祥林,李晓红,等.MathCAD在数学实践中的应用[M].北京:北京航空航天大学出版社,2002.
