基于物理规划的履带起重机变幅系统多目标优化

高 顺 德， 陆 霞， 周 杨， 徐 金 帅

（1.大连理工大学 机械工程学院，辽宁 大连 116024；2.大连益利亚工程机械有限公司，辽宁 大连 116025）

0 引 言

履带起重机的起重性能由臂架强度、整机倾覆稳定性和拉板、钢丝绳等附件强度共同决定.变幅系统的主要作用是实现变幅并且承受由起升荷载和起重机自重引起的构件受力.合理的变幅系统型式和参数设计可以减小相关构件受力，特别是臂架结构荷载，同时提高由臂架强度和附件强度决定的起重性能.因此，对履带起重机变幅系统进行优化设计具有实际意义.

目前，国内履带起重机变幅系统大多采用与同类机型相类比的设计方法；而国外主要在企业内部研究，对于此方面的学术研究较少.王重华等对人字架型式的变幅系统建立以臂架与人字架重量之和最小的优化模型，并采用序列二次规划进行连续变量求解［1］.王欣对人字架加桅杆型式的变幅系统建立构件铰点位置及长度优化模型，以标准型起臂工况的拉板力、变幅绳力和桅杆力为优化目标，采用基于权重法的小生境多目标遗传算法进行求解［2］.齐克奇采用遗传算法对桅杆型式的变幅系统建立优化模型，其优化工况增加了最大臂长最小幅度工作工况［3］.

上述文献对变幅系统的优化进行了探索，但是在实际应用中还存在若干问题.

首先，随着吊装整体化及大型化的发展，超起型工况已经成为中大吨位履带起重机的必备配置，因此有必要在变幅系统优化中将标准型和超起型统一考虑，使得整机优化结果更加切合实际.其次，目前多目标优化问题较多采用权重法，而在设计中很难定义一组恰当的权重保证优化的有效性和准确性，这给设计人员在实际应用中造成了很多的困难.最后，现有文献的优化都是基于连续型变量，但在实际设计中都是采用离散化的设计，这就需要根据设计经验对连续优化结果进行圆整.

鉴于目前中大吨位履带起重机普遍采用桅杆型式的变幅系统，本文针对此类机型，统一考虑标准型和超起型工况，分析其变幅系统的受力特点，建立多目标优化力学模型.为了避免权重设计，采用由Messac于1996年提出的基于偏好设计的物理规划方法［4－5］，通过定义构件期望受力的偏好区间，设计优化目标的综合评价函数.将遗传算法和混沌搜索［6－8］相结合，设计基于Pareto支配的多目标混沌遗传算法，对优化变量离散化处理，采用多目标优化函数求Pareto解集和综合评价函数选择精英解集，在算法后期进行混沌局部搜索不断逼近问题的Pareto最优前端，以降低陷入局部最优解的可能性，避免过早收敛.

1 变幅系统力学模型

1.1 变幅原理

履带起重机的变幅系统是实现其臂架变幅作业的重要承载构件.根据起重能力的不同，起重机可分为标准型和超起型，如图1所示.桅杆式履带起重机的标准型变幅系统由主臂拉板、桅杆和将转台与桅杆相连的主变幅绳组成，通过调整主变幅绳实现主臂变幅.超起型增加了超起变幅系统，包括超起桅杆、超起配重和用于连接的拉板.超起工况作业时通过调整超起变幅绳实现主臂变幅，而桅杆和主变幅绳仅在起臂时工作.

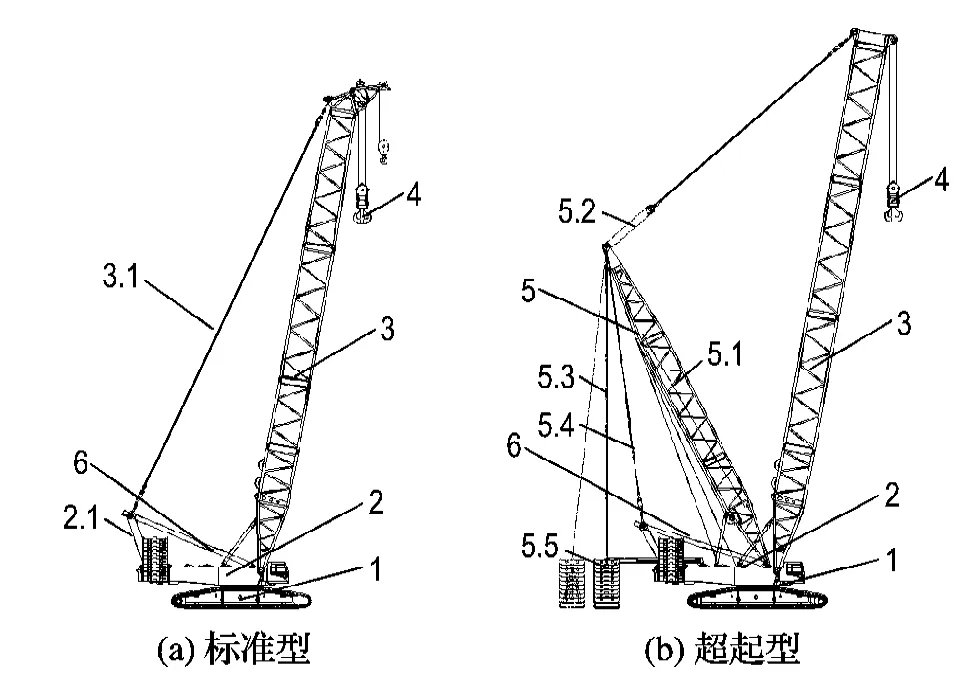
图1 桅杆式履带起重机整机布置图Fig.1 Whole arrangement of mast crawler crane

1.2 力学模型

根据桅杆式履带起重机的工作原理，分别对标准型和超起型主臂工况建立力学模型.考虑主臂自重，其他杆件自重不计，不考虑构件变形对受力的影响，配重型式为托盘式悬浮配重.在变幅平面内风从后往前吹，几何模型如图2所示.各铰点定义为主臂铰点B，桅杆铰点A，主变幅铰点C，桅杆上铰点E，主臂上铰点I，主臂拉板铰点Ig，主臂导向轮铰点Ish，主臂起升铰点Iq，超起桅杆铰点D，超起桅杆顶点N.无特殊说明角标d为超起型标志.

1.2.1 标准型模型 分析臂架荷载特点，铰点Iq处受力见下式：

式中：Q是特定臂长下的额定起重量；θq是货物在风力和回转机构启动或制动惯性力作用下偏离铅垂线的角度.

图2 履带起重机模型简化图Fig.2 Simplified model of crawler crane

根据力矩平衡原理，基于铰点B建立方程，主臂拉板力Fg、主变幅绳力Frg和桅杆力Fzh的数学表达式见下式：

式中：L是主臂长度；cg是主臂的重心比（根轴到重心位置与主臂长度的比值）；G是主臂自重；LBsh是主臂铰点B到起升绳的距离；LBg是主臂铰点B到拉板的距离.

1.2.2 超起型模型 超起型主臂拉板力计算方法与标准型相同，根据力平衡原理，超起后拉板力Fdg、超起桅杆力Fd、超起主变幅力Frgd和超起桅杆力Fzhd的数学表达式见下式：

式中：Gp是超起配重重量；θjp＝θsd＋θp－90°，是超起配重与超起桅杆轴线的夹角.

1.3 构件受力趋势分析

通过分析发现，对于主臂拉板力、臂架力、超起桅杆力和超起后拉板力，桅杆越长对构件受力越好，但是对于超起工况的桅杆力和主变幅绳力，桅杆越长对构件受力越不好.拉板长度对主臂拉板力、桅杆力和主变幅绳力影响较大，变化关系复杂.桅杆角度越大对桅杆力和变幅绳力越好，但需要保证桅杆与转台不干涉.超起桅杆长度越长对主臂拉板力和臂架力越好，但考虑到经济性应该越短越好.

1.4 优化目标

从构件受力趋势分析可以看出，臂架力、主臂拉板力、超起桅杆力、超起后拉板力、桅杆力和主变幅绳力，在设计时存在耦合计算，不易确定最优设计组合以使系统受力最小.

计算变幅系统受力时考虑风从后往前吹，主臂强度计算时要综合考虑轴向荷载和弯矩（此时风从侧向吹），在一定程度上拉板力体现了臂架的受力变化趋势，因此优化时不考虑臂架力［2］.

因此，模型的优化目标共5个，分别是主臂拉板力、超起桅杆力、超起后拉板力、桅杆力和主变幅绳力.

1.5 优化变量

选取影响变幅系统中构件几何关系的10个变量作为优化变量，分别是桅杆铰点A（xA，yA）、主变幅铰点C（xC，yC）、超起桅杆铰点D（xD，yD）、主臂拉板长度Lg、超起桅杆长度Ld、超起后拉板长度Ldg、桅杆长度Lzh.

对于人字架式履带起重机，主变幅滑轮组铰点可看作人字架顶点，因此上述模型中若将标准型主板拉板长度、桅杆长度省去，即可变成适应人字架式系统的8个变量的变幅系统优化模型.

1.6 优化工况

选取变幅系统中构件受力较大的5类工况作为优化工况，分别是标准型最大臂架的起臂工况和最大幅度工况、标准型最短臂架的最大幅度工况、超起型最长臂架和最短臂架的最大幅度工况.

目前一般采用许用应力法进行起重机设计，即材料、零件、部件的许用应力值根据极限应力除以安全系数确定.根据文献［9］，工作工况和起臂工况的荷载组合分别为B和C，相应的安全系数为1.34和1.22，设计时需要将起臂工况统一折算到工作工况.优化目标计算时取5类工况中构件受力的最大值进行优化.

1.7 约束条件

优化变量的范围需要遵循以下设计原则：

①铰点D在B的左上方；

②铰点A在D的左上方；

③铰点C在A的左侧；

④铰点C到桅杆AE的距离不小于LCAEmin；

⑤铰点A到变幅绳CE的距离不小于LACEmin；

⑥铰点E到超起桅杆DN的距离不小于LEDNmin；

⑦标准型工况铰点E在直线CI上方；

⑧超起型工况铰点E在CN上方；

⑨铰点C和E的水平坐标｜x｜小于铰点N的水平坐标｜x｜；

⑩铰点A和D位于相对回转中心x正方向，C位于相对回转中心x负方向；

瑏瑡超起桅杆长度Ld不大于最短超起主臂长度.

最少输入约束参数为XAmin、YAmax、XCmin、YCmin、YCmax、LCAEmin、LACEmin、LEDNmin.其他约束值通过遵循设计原则的几何关系确定，如图3所示.

图3（a），通过设计原则 ④⑥ 确定Ldmin＝｜DN″｜，通过设计原则 瑏瑡 确定Ldmax.

图3（b），在Ld已知情况下，通过设计原则④⑧确定Lzhmin1＝｜AE″｜，通过设计原则⑥⑨确定Lzhmax＝｜AE′｜.

图3（c），通过设计原则 ④⑦ 确定Lzhmin2＝与图3（b）中确定的Lzhmin1比较取较大值.

图3（d），在Lzh已知情况下，通过设计原则④确定Lgmax＝｜IgE′｜.

图3（e），在Lzh已知情况下，通过设计原则⑤确定Lgmin＝｜IgE″｜.

图3（f），在Ld和Lzh已知情况下，通过设计原则⑧确定Ldgmin＝｜NE″｜，通过设计原则④确定Ldgmax＝｜NE′｜.

在初始化和优化算法中优化变量的边界值需要按D、A、C、Ld、Lzh、Lg、Ldg的顺序确定.

1.8 多目标优化模型

通过上述分析，履带起重机变幅系统优化问题的数学模型可表示成下式：

图3 优化变量几何关系Fig.3 Geometrical relations of optimization variables

2 基于物理规划的综合评价函数

2.1 物理规划类型

物理规划根据设计者偏好将量化的指标表达成量纲一的偏好函数，定义成6个梯度的满意度区间，分别是不可接受、高度不期望、不期望、可容忍、期望和高度期望.物理规划中定义了4种基本偏好函数类型，即指标越小越好的类型1、指标越大越好的类型2、指标趋于某值的类型3和指标在某范围内的类型4，并且每类函数均具有软（S）和硬（H）的情况.

1S型偏好函数如图4所示.设计函数值Fi为横坐标，偏好函数值gi为纵坐标.在非线性偏好函数中区间的边界要求连续可导，因此偏好函数构造时需要通过调整参数保证二阶导数严格为正［4］.

图4 1S偏好函数的满意度区间Fig.4 Satisfaction regions of preference function 1S

2.2 基于物理规划的综合评价函数

多目标优化算法的最优解实际上是Pareto最优解，其搜索过程就是将非劣解集不断逼近Pareto前端.在搜索过程中需要根据决策者对解集的偏好选择Pareto最优解.基于物理规划的变幅系统综合评价函数见下式：

式中：gzi［Fzi（lz）］为某优化目标项的偏好值；fzi5为偏好函数的约束值，由设计者给定.

3 多目标混沌遗传算法

遗传算法是一类模拟生物自然选择与进化的随机搜索算法.本文根据遗传算法通用求解框架［10］和已有的多目标遗传局部搜索算法（MOGLS）［11］，设计多目标混沌遗传算法（MCGA），算法流程如图5所示.

采用适用于实数编码的适应度值比例法选择策略、模拟二进制交叉策略和多项式变异策略进行遗传搜索.优化变量在初始化和进化过程中始终根据设计精度离散化.为了防止算法过早收敛，构建完全混沌局部搜索［8］，利用混沌变量的随机性、遍历性等内在特性，更新非劣解，保持种群的多样性.

种群根据多目标函数Fz采用Pareto支配［12］更新非劣解集ND，并根据综合平衡函数gz采用精英策略从ND中选择优良个体直接进入下一代进化，以便破坏个体性态.

图5 MCGA流程图Fig.5 Flow chart of MCGA

4 算例分析

对本课题组与大连重工集团有限公司联合开发的QUY750履带起重机变幅系统进行优化.标准型主臂长度为24～84m，超起型主臂长度为36～96m，臂架最大仰角为84°，超起桅杆幅度为13 m.数学模型参数如表1所示.

优化过程中对变量进行离散化，铰点坐标、桅杆和超起桅杆长度、拉板长度的最小变化值分别为0.005、0.5、0.1m.

优化工况见表2.起重量仅考虑臂架强度和整机倾覆稳定性.由于此机型的超起配重采用油缸变幅，计算时增加了不同超起配重幅度的工况.

对QUY750主变幅系统的构件参数进行优化，根据其受力的特点，优化目标应小于设计最大荷载，故偏好函数均为1S型.偏好区间定义见表3.

优化算法种群规模80，精英个体集规模20，最大进化代数50，模拟二进制交叉概率0.85，多项式变异概率0.1.每个优化变量的混沌搜索概率1，进行局部搜索的个体数量2，每个被选中的个体的拷贝进行混沌搜索的最大次数5.

通过上述参数的设置，根据第3章的进化算法编写Matlab程序.对每一代的个体按照评价函数进行排序，均布选取20个个体，其进化历程如图6所示.初始种群的偏好值均较大，不满足要求的极限荷载，第10代部分个体得到较优解，第10代与第20代之间种群整体优化水平得到快速提高，第20代之后优化过程全部进入缓慢的局部寻优阶段.由于增加了局部搜索，种群在进化过程中，始终有部分个体保证多样性，防止算法过早收敛.

表1 数学模型参数列表Tab.1 Parameter list of mathematic model

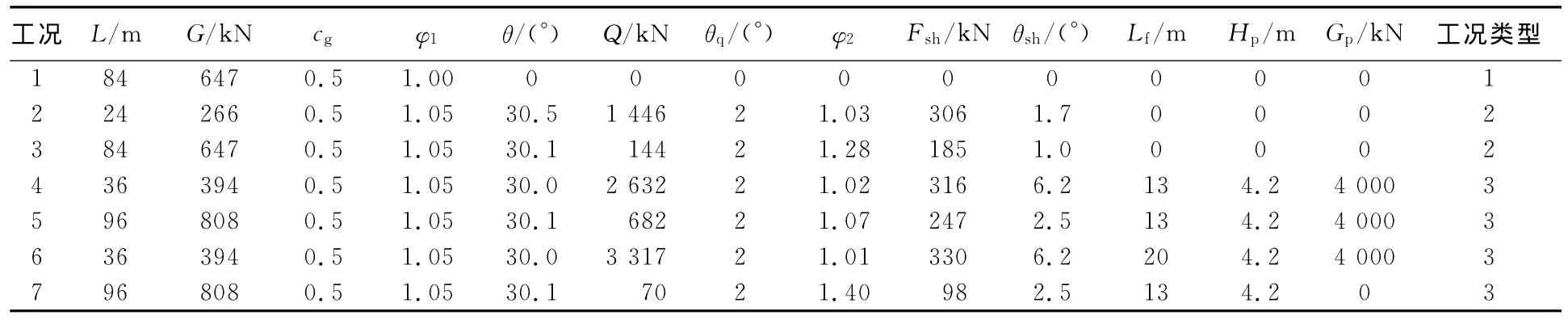
表2 优化工况Tab.2 Optimization conditions

表3 设计目标的偏好区间Tab.3 Preference regions of design objectives

图6 种群的进化历程Fig.6 Evolutional progress of population

根据表3定义的偏好函数区间边界值，优化目标的物理规划进化历程如图7所示.算法最优解集在第6代后偏好值有明显优化趋势，进入局部搜索区域.在第7代后每一代的最优个体通过混沌搜索进行局部寻优，进一步确定优化解集，变化不明显.如此，算法保证多样性的同时能较快缩小搜索范围，最大程度发挥混沌搜索在局部搜索区间的优势以寻找最优解.

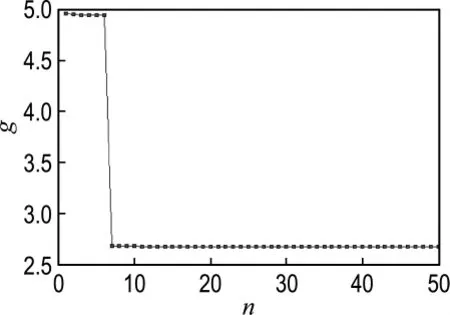
图7 优化目标的物理规划进化历程Fig.7 Physical programming evolutional progress of optimization objectives

优化计算结果见表4.与原始设计值相比，桅杆长度减小，超起桅杆长度增加.对转台上的铰点位置进行了优化，使得拉板力、变幅绳力、超起后拉板力和超起桅杆力均减小，而桅杆力略有增加.基于物理规划的偏好函数对于超出可行区间的值将予以较大的惩罚值，故表中原始的设计值会出现很大的偏好值.

表4 优化结果比较Tab.4 The comparison of optimistic results

5 结 论

（1）将影响履带起重机变幅系统构件几何关系的参数作为优化变量，全面地选取典型工况进行优化，使优化模型更加完善，符合日益复杂的设计要求.

（2）利用物理规划方法建立优化目标的综合评价函数，取代了基于权重的优化方法，使设计人员能够更加精准地表达设计要求.

（3）优化变量离散化，采用基于Pareto支配的多目标混沌遗传算法进行求解，结合多目标函数和评价函数选取精英解集和进行遗传、混沌搜索，使算法有方向性地进行最优解搜索.通过实例分析验证了本文提出优化方法的有效性，对实际设计具有指导意义.

［1］王重华，王培基，章一计，等.起重机臂架与人字架的综合优化设计［J］.工程机械，1992（5）：14－16.WANG Chong－hua，WANG Pei－ji，ZHANG Yi－ji，etal.Comprehensive optimum frame design of boom and derrick in cranes ［J］.Construction Machinery and Equipment，1992（5）：14－16.（in Chinese）

［2］王 欣.大型履带式起重机设计的关键问题研究及软件系统研制［D］.大连：大连理工大学，2001.WANG Xin.The key problems of large crawler crane designing and software system ［D］.Dalian：Dalian University of Technology， 2001.（in Chinese）

［3］齐克奇.大吨位履带起重机上车主要参数的计算与优化［D］.长春：吉林大学，2009.QI Ke－qi.The calculation and optimization of main structural parameters of the upper－car of large tonnage crawler crane ［D］.Changchun：Jilin University，2009.（in Chinese）

［4］Messac A.Physical programming： effective optimization for computational design ［J］.AIAA Journal，1996，34（1）：149－158.

［5］Lewis K E，Chen Wei，Schmidt L C.Multiobjective decision－making using physical programming ［M］／／ Messac A，ed.Decision Making in Engineering Design.New York：ASME Press，2006：155－170.

［6］Determan J，Foster J A.Using chaos in genetic algorithm ［C］／／Proceedings of the 1999Congress on Evolutionary Computation.Piscataway：IEEE Press，1999：2094－2101.

［7］Caponetto R，Fortuna L，Fazzino S，etal.Chaotic sequence to improve the performance of evolutionary algorithms［J］.IEEE Transactions on Evolutionary Computation，2003，7（3）：289－304.

［8］雷德明，严新平，吴智铭.多目标混沌进化算法［J］.电子学报，2006，34（6）：1142－1145.LEI De－ming， YAN Xin－ping， WU Zhi－ming.Multi－objective chaotic evolutionary algorithm ［J］.Acta Electronica Sinica，2006，34（6）：1142－1145.（in Chinese）

［9］中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB／T 3811—2008起重机设计规范［S］.北京：中国标准出版社，2008.General Administration of Quality Supervision，Inspection and Quarantine of the People′s Republic of China，Standardization Administration of the People′s Republic of China.GB／ T 3811－2008 Crane Design Specifications［S］.Beijing：Standards Press of China，2008.（in Chinese）

［10］Back T， Schwefel H P.An overview of evolutionary algorithm for parameter optimization［J］.Evolutionary Computation，1993，1：1－23.

［11］Arroyo J E C，Armentano V A.Genetic local search for multi－objective flow shop scheduling problems ［J］.European Journal of Operation Research，2005，167（3）：717－738.

［12］雷德明，严新平.多目标智能优化算法及其应用［M］.北京：科学出版社，2009：32－33.LEI De－ming， YAN Xin－ping.Multi－objective Intelligent Optimization Algorithm and Its Application［M］.Beijing：Science Press，2009：32－33.（in Chinese）