液压管路中两种分析方法的数学建模与比较①

2013-09-27单长吉

佳木斯大学学报（自然科学版） 2013年6期

关键词：压缩性管路流体

单长吉

(昭通学院物理与电子信息工程学院，云南昭通 657000)

0 引言

为进一步分析流体压力和流量的变化及外界的干扰对管路振动的影响，需要对管路系统的动特性进行适当分析，以确定不同管路的振动频率和及其特性，以便探明降低管路振动噪声的途径.

1 管路的动态特性方程

一般求解管路动态特性的方法常有:能量法、波动法和频率法等.能量法不考虑系统的压缩性，因而不能考虑波动现象，其使用范围有限.波动法考虑流体的压缩性，但通常不考虑流动的粘性阻力和系统的弹性耗损，因此得不到波动的衰减过程，故此方法适用于求液压冲击.而频率法既考虑流体的压缩性，又考虑流体的粘性，因此广泛用于计算管路系统的动态特性.本文主要针对集中参数法和分布参数处理法两种分析方法求解管路的动态特性.

1.1 集中参数法数学建模

集中参数法:当管路较短，变量的脉动频率较低，管路内的液体可视为一个集中的质量，管路内的摩阻及液体的压缩性、管道的弹性变形可集中在一处，作为集中参数处理.而当管路较长，变量的脉动频率较高，其液体的质量，管路的摩阻及液体的压缩性通常认为是沿程分布时，若按集中参数法处理就显得过分粗略，而且计算误差太大，则应作为分布参数法处理[1].

(1)流体的连续性方程

如图1所示.根据流体的连续性方程，流入断面1－1和流出断面2－2的液体流量之差，应等于管路内液体的压缩和管路膨胀体积之和，即

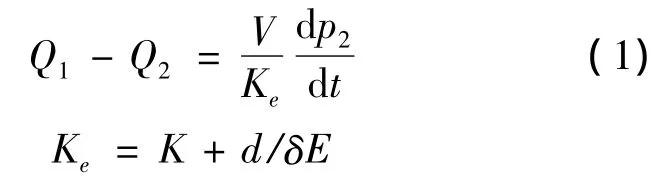
式中:V为管路的体积;A为管路的面积;Ke为表观体积弹性模量;L为管路的长度;K为液体的体积弹性模量;d为管径;δ为管壁厚度;E为管路的弹性模数

图1 集中参数液压管路

式中:ρ为液体密度;Rf为层流的管路摩擦阻力.Rf=RvρLQ2

(2)管路内液柱的运动微分方程

υ为油液的运动粘度，(Pa·s)

对(1)和(2)两式进行拉氏变换得

(3)至(6)式即为按集中参数法求解的管路动态特性的基本方程，它表示了管路进、出口压力和流量之间的相互关系[2].

其传递函数为:

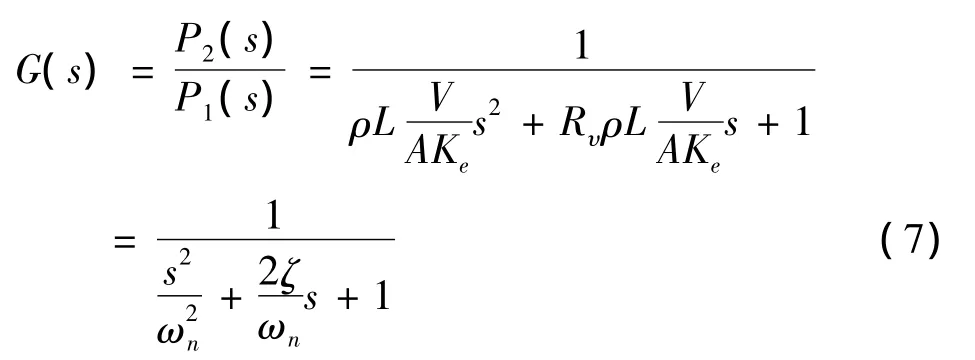
式中:ωn管路无阻尼液压固有频率;

Rf为层流的管路摩擦阻力;Kh为液压弹簧刚度;M为管中的液体质量;c为压力波传播速度;ζ为管路的阻尼比

图2 分布参数液压管路

1.2 分布参数法数学建模

如图2所示，入口压力和流量分别为P1，Q1，出口的压力和流量分别为P2和Q2，距断面1—1为x处的压力和流量为P和Q.现列写长度为的单元液体的微分方程为[3～4]:

(1)运动微分方程

x=0时:P(s)=P1(s)，Q(s)=Q1(s);

x=L时:P(s)=P2(s)，Q(s)=Q2(s)求得待定系数 K1，K2，并代入(12)，(13)式得

代入求得二阶偏微分方程为

(14)和(15)两式为按分布参数求解的管路动态特性基本方程，亦称管路输出基本方程.它表示了输入端参数 P1(s)，Q1(s)和输出端参数 P2(s)，Q2(s)之间的线性变换关系.

将(14)(15)和(16)写称矩阵形式为

2 两种方法的比较与分析

从(7)式可以看出集中参数法的特点:对闭端管路按集中参数处理时，可以将其等效为单自由度二阶系统.二阶系统的无阻尼自振频率ωn与液压弹性刚度Kn和液体质量M有关.ωn与压力波(声波)的传播速度成正比，与管长成反比，管长愈短，则自振频率愈高.

从(17)式可以看出分布参数法的特点:对于液压管路按分布参数法处理时，可以将其等效为传输矩阵与初端—终端之间的压力和流量的数学关系.且与管路的长度和管径的大小有着密切的关系[5].

分布参数法对于任何长度，任何压缩比的流体都是适用的.如果在可以忽略一定因素的情况下，用集中参数法来替代分布参数法也是可行的.将式(5)，(6)与式(16)联立，采用近似方法，可得:

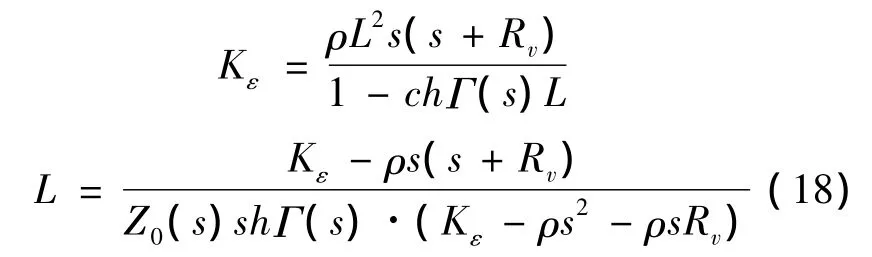
式(18)将分布参数法和集中参数法的参数之间联系在一起，可以得到体积弹性模量与管路长度的表达式.对于一个液压管路，影响的因素很多:油液的运动粘度，体积弹性模量，油液的密度，管路的长度，油中音速等.由于这些参数之间存在着复杂的数学关系，所以定量(例如管长的具体数值，管径的面积具体数值)来限定集中参数法的应用范围是不可行的.但可以采用K和L两个参数指标来考量是否可以采用集中参数法来对管路进行分析.当时，采用集中参数法来分析;反之，采用分布参数法分析.