工作台平面度的检验

付承云 刘莲花 罗秀珍

(大连机床集团有限责任公司，辽宁大连 116600)

在 GB/T 17421.1－1998(eqvISO 230－1∶1996)《机床检验通则 第1部分:在无负载精加工条件下机床的几何精度》标准中，对平面度的定义及检测工具提出了原则要求。本文依据标准要求，结合机床行业实际情况，对工作台平面度检验方法及数据处理做一下详细介绍，以便检验人员掌握工作台平面度的判定。

所谓平面度是指在规定范围内，被检面上的各点，到平行于该面总轨迹的基准平面的垂直距离的变化，小于规定值时，则该面是合格的。基准平面可用一平板或用移动平尺所得的一组直线来表示，也可用水平仪或光束来表示。目前在国际上评定平面度误差有多种方法，如“两点法”、“三点法”、“最小条件法”、“最小二乘法”以及“角值法”、“四点法”等等。但是，就机床精度标准中的平面度检验而言，我们主要采用了“两点法”或“三点法”。本文主要介绍一下“三点法”。

所谓“三点法”，就是以通过被检平面上的三点(一般是选择相距最远的三点)的平面作为基准平面，被检平面上的各测点到基准平面的坐标值，即为各测点相对于基准平面的偏差。各测点偏差的最大代数差值，即该平面的平面度误差。

“三点法”具有以下特点:

(1)有基准平面的含义。它具有一个统一的评定误差的基准，因此，较“两点法”更加合理。

(2)“三点法”的测量结果不是唯一的。由于决定基准平面的3个点的位置不同，对矩形平面共有4种组合形式(见图1)，所以从工艺上就要保证任一种组合形式的检验都要合格。

(3)用“三点法”所测得的误差值较大，在一般情况下，比其它的方法要求都严。

(4)“三点法”比较简便，可用作图法或计算法求出平面度误差，适用于生产现场。

下面举例介绍平面度误差的计算法。

例:某矩形工作台尺寸为B×L=950 mm×1 200 mm，求该工作台的平面度误差。

采用0.02 mm/1 000 mm的水平仪及桥板(跨距a=200 mm、250 mm)，按网格布点进行测量，如图2所示。

从A点(零点)开始，按图2中的箭头方向采用两点连锁法进行测量，测得水平仪读数(格数值)见表1。

表1 格

为了便于数据处理，应首先求出各测点相对于通过A点(零点)的水平面的高度差，即按测量方向，将各测点的水平仪读数相叠加，也就是从零点开始，将各段所测得的读数累计相加。如表1中AB线的第一段读数为－0.5格，第二段为－0.5格，第三段为 +1.5格，第四段为 +1.5 格。

第一段 加后为:0+(－0.5)=－0.5(格)

第二段 加后为:－0.5+(－0.5)=－1.0(格)

第三段 加后为:－1.0+(+1.5)=+0.5(格)

第四段 加后为:+0.5+(+1.5)=+2.0(格)

同理，AD线的叠加方法与AB线相同，叠加后它们依次为 －1.0格、－2.5格、0格和 +2.0格。但在A1B1线叠加时，要考虑A1B1线起点A1的情况。因A1点是 －1.0格，就要把 －1.0格叠加进去。要特别注意，因水平仪在纵向和横向上每格的线值(mm)不同，

纵向:0.02 mm/1 000 mm ×250 mm=0.005 mm=5 μm

横向:0.02 mm/1 000 mm ×200 mm=0.004 mm=4 μm

所以要把A1点的格数转换成4.0

μm。这样将A1B1线各段的读数转换成线值后，在各段上都要加4.0 μm。同样A2B2线的相加情况也要把起点A2相加进去，A3B3线、DC线的处理也以此类推。(若水平仪在纵横向上的跨距相同，可直接将格数相加)，转换后的数值见表2。

A2B2线上的第三段:－2.5+3X+2Y= －14.0 μm

A3B3线上的第四段:+10.0+4X+3Y= －6.0 μm

DC线上的第四段:+10.5+4X+4Y= － 7.5 μm

各测点修正后的偏差值见表3。

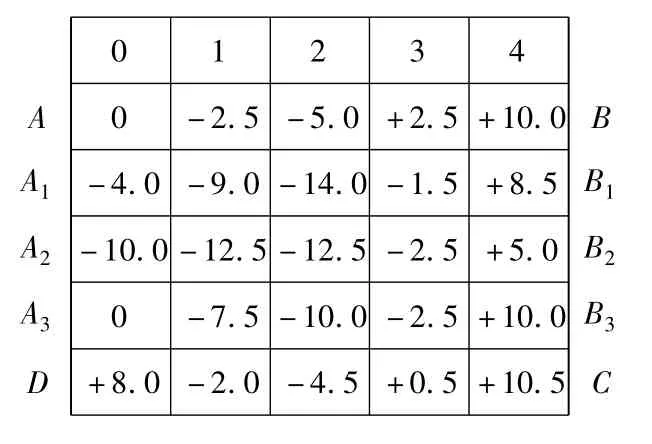
表2 μm

表2所列的数值为各测点相对于通过A点(零点)的水平面的高度差，这个差值并未真实地反映出工作台自身的平面误差。要真正反映出这个误差，必须通过A、B、D三点建立一个基准平面，那么这个基准平面上的A、B、D三点的高度差均为0。从表2可以看出，B点相对于通过A点的水平面的高度为+10.0 μm，D 点为 +8.0 μm，为了使 B、D 两点均为0，所以在 B 点应减去 +10.0 μm，D点应减去 +8.0 μm，同时其余各点要按正比例关系作相应的修正。也就是说，要使通过A点的水平面以A点为支点转一角度，使之成为通过A、B、D三点的基准平面。

修正过程是这样的:先求出纵横向上各段的修正系数X、Y。如纵向AB线上共分为四段，设每一段为一个X，因在第四段B点需减去+10.0 μm，则通过B点求得:

4X= －10.0 μmX= －2.5 μm

同理，在横向AD线上每段设一个Y，则通过D点求得:4Y= －8.0 μmY= －2.0 μm现在修正AB线上第一段:－2.5+X= －2.5+(－2.5)= －5.0 μm

修正AB线上第二段:－5.0+2X=－10.0 μm

修正AB线上第三段:+2.5+3X=－5.0 μm

修正 AB线上第四段:+10.0+4X=0 μm

同样 AD 线上的 A1、A2、A3、D 四个点

分别以Y为系数修正为:－6.0 μm、－14.0 μm、－6.0 μm、0 μm。

但是，A1B1线、A2B2线、A3B3线、DC线的修正方法与AB线和AD线的修正方法不同。AB和AD线分别为X方向(纵向)和Y方向(横向)上的轴线，所以可只按一个方向修正，但其它线由于受到X、Y两个方向的影响，所以每个测点都要在X、Y两个方向上同时修正。

如:A1B1线上的第一段:－9.0+X+Y= －13.5 μm

从表3中可以看出，最高点的偏差为 0，最低点的偏差为 －21.5 μm，因此该工作台的平面度误差为:δ=0－(－21.5)=21.5 μm

此外还有作图法。作图法就是利用表2所示数据，分别作 AD、AB、A1B1、A2B2、A3B3、DC 的误差曲线，从中求出基准平面后得出平面度误差。由于计算法使用起来比较方便，又容易掌握，所以这里对作图法就不再作详细介绍了。