基于主成分降维的总悬浮物浓度遥感估算模型适用性分析*

郭宇龙，李云梅，吕 恒，王珊珊，王永波

(南京师范大学虚拟地理环境教育部重点实验室，南京210023)

常规的水质监测调查速度慢、监测周期长，难以满足对大面积水体水质监测的要求，遥感技术可以克服常规水质监测方法的不足.遥感反射率是湖泊水色的综合反映，是水体光学活性物质吸收和散射相互作用的结果，遥感监测水质最重要的就是建立水质参数和遥感反射率光谱之间的响应关系［1］.近年来，随着高光谱技术的迅速发展，传感器光谱分辨率不断提高，使得遥感反射率能够体现水色要素的细节变动，从而提高水质参数反演的精度［2］.水体中悬浮颗粒物是重要的水色要素之一，总悬浮物浓度(CTSM)通过影响水体的透明度、浑浊度和水色等光学性质，进而影响到水体的生态条件和初级生产力［3］.目前国内外许多学者通过很多方法实现了悬浮物浓度的估算［4－7］，其中(半)经验方法具有简单快速的优势，而且需要获取的参数少，是最常用的估算模型构建方法.传统的经验方法包括单波段法、波段比值法、光谱一阶微分法等［8－10］.然而这些算法只能利用高光谱信息的某个或几个特征波段，建模过程中波段的选择和波段组合的方式，都包含很多不确定因素(例如不同时期获取的数据、最佳估算波段会有所差别)，如果都使用相同的敏感波段，会导致最终得到的统计回归模型未必是最佳估算模型.

更多的波段会包含更多的有用信息，然而同时采用大量波段进行统计回归又存在以下问题:高光谱数据相邻波段相关性很高，容易出现数据冗余，此外，如果将大量自变量都参与多元线性回归分析，在增加计算量的同时，也会使模型过于复杂，不便使用.偏最小二乘法［11］可以较好地解决这个问题，但对高光谱数据来说，偏最小二乘回归很难得到一个简洁的回归方程，不利于模型的分享，也不便应用于遥感卫星影像.因此本研究利用主成分分析法，对高光谱数据进行降维处理，以期利用较少的主分量综合反映水体光谱信息.进而利用得到的几个互不相关的主成分对指数变换之后的悬浮物浓度进行多元回归拟合，建立悬浮物浓度估算模型.最后通过实验，确定模型的最适宜分量数以及利用该方法时高光谱数据的适宜波段数;并对该模型算法的遥感影像适用性进行分析，以期提高内陆Ⅱ类水体水色参数反演的精度，并挖掘该模型在不同遥感卫星影像上应用的潜力.

1 材料与方法

1.1 研究区域

本研究以太湖为研究区.太湖位于长江三角洲南缘，是我国第3大淡水湖泊，流域总面积36500 km2，湖体面积 2338 km2，平均水深 1.89 m［12］.

1.2 数据的获取

分别于2009年4月16-27日、2011年5月20日对太湖进行野外采样，其中2009年4月共采集54个样本，2011年5月共采集30个样本(图1).在每个采样点获取水面遥感反射率，水体反射光谱的测量采用美国ASD公司生产的ASD FieldSpec Pro便携式光谱辐射计，其波段范围为350～1050 nm.为减少水体镜面反射和船体自身阴影的影响，测量时采用唐军武等［13］提出的内陆Ⅱ类水体水面以上光谱测量的方法.提取遥感反射率时需要测量的数据包括标准灰板、天空光、水体等的光谱辐亮度信息，每个对象都要采集10条以上的光谱数据，剔除异常光谱数据，剩余数据做均值处理.遥感反射率提取的具体方法见文献［14］.在光谱测量的同时采集表层水样，低温冷藏带回实验室测量悬浮物的浓度.悬浮物浓度采用常规的干燥、烘烧、称重法(GB/T 11901-1989)测定.

图1 太湖采样点分布Fig.1 Distribution of sampling sites in Lake Taihu

1.3 数据的处理

为了消除不同观测时间的光谱差异，对每条遥感反射率光谱曲线进行归一化处理(公式(1))，突出光谱特征［15］.

式中，Rrs(λ)和Rrsn(λ)分别为归一化前、后波长λ处的遥感反射率，n为可见光波段参与计算的波段数，本研究为381.本研究将通过归一化前后的遥感反射率与待估算参数之间的相关性，分析归一化前后遥感反射率对总悬浮物浓度的敏感性.

1.4 遥感反射率主成分分析

主成分分析就是用少数几个主成分来描述多个指标或因素之间的联系，以较少几个主成分反映原数据的大部分信息的统计方法.从数学角度来看，是一种降维处理技术［16］.经分析得到的主成分用PCi表示，如PC1代表第一主成分，PC2代表第二主成分，以此类推.

分解得到的特定主成分代表一组光谱的某个特征，这种特征体现在该主成分的载荷系数上.研究将通过分析不同主成分的载荷系数，解释不同主成分在模型构建中的作用.

1.5 基于主分量的多元线性回归建模

高光谱数据的各个主成分之间是没有相关性的，因此以这些主成分为自变量，待反演参数作为因变量，建立多元线性回归模型，用来估算悬浮物浓度.模型如下:

式中，y为待反演的参数，这里是ln(CTSM)［17］，n为主成分个数，ai为第i个主成分的系数，b为截距项.理论上，有多少个高光谱波段，就有多少个成分分量.因此确定模型中n的大小也是一个关键问题.本研究以迭代运算的方式，确定参与建模的主成分个数.

1.6 模型的评价方法

1.6.1 模型精度评价指标 研究中用于评价模型的指标均方根误差(RMSE)和平均相对误差(MAPE)分别利用式(3)、(4)计算得到:

式中，yi、y'i分别为实测悬浮物浓度和估算悬浮物浓度，n为样本数.本研究将2009年4月实验获取的数据分为两部分，随机抽取其中的36组遥感反射率及与其对应的总悬浮物浓度作为建模数据，用公式(2)来构建总悬浮物估算模型，剩余的18组数据作为验证数据，用来验证模型的精度.2011年5月实验获取的数据全部作为独立数据，对模型进行独立验证.同时，为了对比分析，用相同的数据建立4个常用的总悬浮物浓度反演经验模型，并与本文模型进行比较.

1.6.2 模型的影像适用性评价方法 实测高光谱数据具有1 nm的光谱分辨率，这是目前的高光谱影像数据都不具备的，因此为了评价本文模型的影像适用性，对模型做了两类实验:实验1:从400～850 nm共451个波段中随机删除一个波段的数据(随机数由IDL中的randumu函数生成)，用剩余的波段进行主成分分析、多元线性回归拟合建立模型，并进行精度评价，如此往复，直到剩余6个波段为止，作为一次实验.重复100次实验，记录每条R2曲线和MAPE曲线，最后取均值.以此讨论一般情况下支持主成分模型需要多少波段.实验2:通过不同传感器的波段响应函数和实测高光谱数据，模拟一些常见传感器的光谱数据集，针对不同传感器模拟光谱进行模型构建，并进行精度评价，以此分析这些传感器对该算法的适用性.

2 结果与分析

2.1 归一化遥感反射率的悬浮物浓度敏感性分析

由于实测的水体反射光谱在850 nm后迅速下降，数据的信噪比降低，噪声过大，因此本研究只针对400～850 nm范围内的光谱数据进行分析.太湖54个采样点在400～850 nm间的反射率光谱曲线具有典型的内陆Ⅱ类水体的光谱特征［18］(图2A).

归一化之后的遥感反射率在保持了原始遥感反射率特征的基础上，各个反射率曲线之间的系统差异变小.同时，归一化前后的相关系数曲线发生较大变化:归一化之前，相关系数曲线在400～850 nm之间集中在0.6附近，在400～533 nm之间呈平稳下降趋势，最小值为0.528，出现在533 nm处;533～710 nm之间平稳上升;710 nm之后趋于平稳，并保持在较高的水平，最大值为0.866，出现在730 nm.所有波段相关系数的方差较小，仅为0.018，说明相关系数曲线在全部波段范围内浮动不大.归一化之后，相关系数曲线保持了相似的变化趋势，在400～527 nm之间呈下降趋势，最小值为－0.898，出现在527 nm处;527～650 nm之间波动上升;650 nm之后，除了在694 nm有一个小的低值区之外，都保持在较高的水平，最大值为0.911，出现在740 nm处(图2B).所有波段相关系数的方差为0.399，表明归一化之后，不同波段与ln(CTSM)的相关系数在全部波段范围内波动较大.

图2 太湖遥感反射率(A)、归一化遥感反射率(B)及与ln(CTSM)的相关系数对比Fig.2 Comparison of remote sensing reflectance(A)，normalized remote sensing reflectance(B)and their correlations with ln(CTSM)in Lake Taihu

通过对比归一化前后的相关系数曲线发现，归一化前后敏感波段的位置变化较小，但数值变化明显.最大正相关系数提高了5.19%，最小负相关系数降低了89.8%，方差提高了2116.6%，可见归一化之后的遥感反射率对总悬浮物浓度的变化更敏感，特别是在510～560 nm波段，归一化之后的遥感反射率与ln(CTSM)的相关性得到大幅度提升，说明归一化方法能够有效突出光谱中的总悬浮物浓度信息.

2.2 主分量涵盖的悬浮物浓度遥感信息分析

图3 Rrsn前三个主成分载荷、贡献率和累计贡献率Fig.3 Loadings，percent variance and cumulative proportion of PC1－PC3of Rrsn

首先从载荷系数曲线来看，主成分的载荷系数能够表明所对应的变量在主成分中所占据的分量，载荷系数的绝对值越大，说明该变量对最终主成分的影响也越大.本研究中Rrsn的前三个主成分载荷曲线如图3所示，其中PC1的贡献率为48.254%，并且载荷系数曲线的特征与 Rrsn－ln(CTSM)相关系数曲线(图2B)特征很相似，同时都在700 nm之后达到一个稳定的高值区;PC2的贡献率为27.654%，载荷系数曲线与Rrsn曲线特征相似，同时在700 nm之后稳定在－0.2左右;PC3的贡献率为18.401%，极小值出现在550 nm附近，对应该范围内的Rrsn反射峰，之后随着波长增加波动上升，在675 nm处达到峰值，对应Rrsn中的反射谷，之后急剧下降，稳定在－0.2附近.从载荷系数曲线来看，PC1包含更多近红外波段的遥感反射率信息，而近红外波段也是悬浮颗粒物的敏感波段，由此推断前3个主成分中PC1涵盖更多的悬浮物浓度信息，而PC2、PC3则更多地体现了其余波段遥感反射率的曲线特征.

此外，通过对比3个主成分与ln(CTSM)之间的相关系数发现，PC1与ln(CTSM)之间的相关系数最大，达到 0.728，验证了之前的结论;同时，PC2、PC3与 ln(CTSM)之间的相关系数分别为 0.401 和 0.403.可见，虽然每个主成分之间是不相关的，但都体现出与ln(CTSM)之间不同程度的线性相关，说明不同主成分可以从不同侧面涵盖悬浮物浓度信息，也说明悬浮物浓度的信息不仅仅包含在其敏感波段中，也有一部分包含在非敏感波段的反射率信息中.

至此，前3个主成分的累计贡献率达到94.308%，理论上已经达到主成分分析的要求，之后的主成分只包含少量信息(整体的5.692%).然而，水体属于弱信号体，细微的差异就可能影响水体组分反演结果;而细节信号与噪声有时很难区分.所以不能采取传统的主成分分析方法中，简单地取累计贡献率大于85%的主成分个数进行应用的做法.本研究中采用迭代运算的方式确定最佳主成分个数.

图4 不同主成分个数下模型的R2、MAPE和RMSEFig.4 R2，MAPE and RMSE of the model using different amounts of PC

2.3 降维悬浮物浓度估算模型的构建及评价

2.3.1 主分量个数的确定及建模 从54组数据中随机抽取36组用作建模，18组用作验证，通过不断增加参与建模的主分量个数，计算模型建立时的R2和验证数据的MAPE及RMSE，确定对悬浮物浓度估算最有利的主成分个数.R2会随着主成分个数增加呈不断上升的趋势(图4)，说明更多的主成分能对悬浮物浓度进行更好的拟合;MAPE和RMSE的变化趋势略有不同，二者都从2个主成分开始平稳下降，到6～8个主成分之间达到谷值区，之后略有升高，15个主成分之后几乎不再变动，说明拟合效果最好的模型，未必是验证估算效果最好的模型.

从迭代结果来看，从2个主成分开始，模型的R2出现急剧上升，与之对应的，MAPE和RMSE也都急剧下降，之后R2趋于稳定，而模型RMSE和MAPE的第二个“突变点”出现在6个主成分处.因此取最佳主成分个数6个来进行多元线性回归模型的构建和验证.6个主成分提取与建模的参数如表1所示.

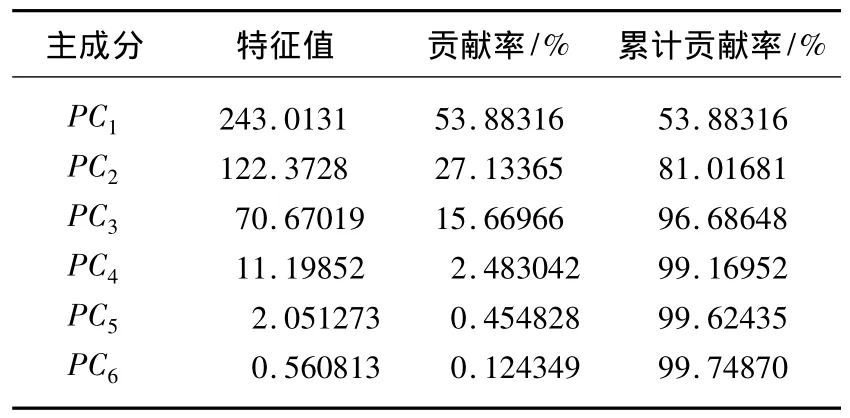
表1 前6个主成分的特征值、贡献率和累计贡献率Tab.1 Eigenvalue，percent variance and cumulative proportion of PC1－PC6

Rrsn中的主要信息都在前3个主成分中得以体现，因为从第4个主成分开始，主成分的特征值、贡献率都有急剧的变化:PC4的特征值和贡献率较PC3减小了84.15%，致使累计贡献率仅提高2.57%，之后特征值、贡献率和累计贡献率都没有大幅度变化(表1).说明PC4～PC6更多地体现了Rrsn中的一些细节部分，这些信息对Rrsn整体的影响不大，但却包含一些估算所需要的信息，因此模型拟合精度(R2)才会有所提高，MAPE和RMSE随之整体降低.而PC6之后的主成分，则更多包含Rrsn中的噪声信息，不能对模型的构建产生积极的作用，模型的MAPE和RMSE也因此随之升高.

在确定了参与建模的主成分个数之后，得到对应的估算模型为:

式中，n=6，a1=0.00219，a2= －0.00365，a3= －0.00015，a4= －0.00398，a5=0.007367，a6=0.124349，b=3.983785.

建模数据集拟合的R2为0.8441，验证数据集的MAPE为0.125，RMSE为12.746.MAPE最小值仅为0.008，最大值为0.749.估算误差MAPE小于10%的采样点共11个，占整体的61%;MAPE小于20%的采样点共16个，占整体的89%.说明该算法可以精确地对悬浮物浓度进行估算.

2.3.2 模型的对比分析 国内外诸多学者利用高光谱数据研发了很多悬浮物浓度的遥感估算模型，一般采用绿光、红光波段或近红外波段来构建模型［19］.在此基础上，本研究构建了不同波段组合与指数变换之后的悬浮物浓度之间的线性回归模型，数据处理都采用相同的方法，以避免由于处理方法不同引入新的误差.最终确定最大相关系数0.823，对应高光谱数据686 nm波段(R686);最小相关系数－0.837，对应高光谱数据528 nm 波段(R528).于是分别以 R528、R686、R686/R528、R686～R528为自变量，ln(CTSM)为因变量，建立线性回归模型，分别记作经验模型一、二、三、四，最后得到的模型参数如表2所示.

无论从建模数据集拟合的R2，还是验证数据集的MAPE、RMSE，本文提出的模型都能得到较好的结果(表2).与传统的4个经验模型相比，本模型的拟合精度分别提高了9.35%、17.07%、10.60%和11.32%，平均提高了12.01%;MAPE 分别降低了49.51%、64.44%、53.87%和53.41%，平均降低了56%;RMSE 分别降低了30.86%、57.66%、39.52%和46.69%，平均降低了45.48%，可以说本模型相比于传统经验模型在整体精度方面有显著提高.

表2 不同模型对比Tab.2 Comparison of different models

由主成分模型和4个经验模型的实测－估算散点图(图5)可以看出，验证数据集中有两个采样点的悬浮物浓度高于150 mg/L，传统经验模型在这两个点的估算中都出现了不同程度的“偏移”现象，特别是34号样点实测悬浮物浓度为237.7 mg/L，4种经验方法中只有1种能将估算误差勉强控制在20%误差线以内，而主成分模型能够很好地估算其浓度，使散点接近1∶1线.说明传统经验模型在进行最小二乘拟合的时候受到一些离群值的影响，导致模型系数偏离最佳情况.因此，在进行传统经验模型构建的时候，往往要剔除一些所谓的“异常值”，然而可能这些离群点中也包含有用信息，只是用单一波段无法将这些信息正确地表达.而主成分模型可以较好地修正这些“偏移”，说明主成分分析提供了一种更加确切的光谱信息提取方法，能有效地利用离群点的有用信息，并反映在最终的估算精度中.

图5 估算与实测总悬浮物浓度对比Fig.5 Comparison of estimated and measured TSM contents

此外，虽然所有5个模型在独立数据中的MAPE相较于验证数据都有所升高，但本文模型仍能将MAPE控制在30%以下，优于4个传统的经验模型，表明该模型更稳定，也更具实用性.

图6 两次实验的估算模型精度Fig.6 Accuracy of the models in the two tests

2.3.3 模型的影像适用性评价 根据1.6.2中描述的方法，通过两组实验对本文模型的影像适用性进行评价.结果表明，实验1中，在波段数多于200时，R2和MAPE几乎没有变化，因此只讨论波段数在200之内的情况(图6).从R2曲线来看，波段的多少对估算模型的拟合精度影响不大，R2平稳保持在0.85附近.从 MAPE曲线来看，在波段数大于100的情况下，MAPE变化同样不大，但随着波段数量继续减少，MAPE开始出现波动上升的趋势，45～100个波段之间上升幅度较小，而波段数小于45之后开始急剧升高，最后接近0.4.说明理论情况下，在400～850 nm之间，波段数量多于45个的传感器数据都可以用来建立悬浮物浓度的主成分模型，并且得到较稳定的结果，但对于波段数量小于45的传感器，模型精度和稳定性无法保证.与Craig等［15］用类似的方法在Ⅰ类水体中的研究结果相比，本研究表明需要更多的光谱来表达水体组分浓度信息，这是因为内陆水体光学性质比较复杂，需要更多的波段信息进行相互补充，才能对其进行精确地表达.

实验2中，共模拟了5种传感器的遥感反射率，分别是 MODIS、MERIS、HJ1－HSI、Hyperion和 CHRIS.国内外诸多学者对这些传感器在水色参数估算方面的应用做了大量研究，如Nechad等提出一种基于多传感器数据的浑浊水体悬浮物浓度反演算法，并用于MODIS、MERIS等传感器［20］;杨煜等基于HJ1－HSI数据应用叶绿素反演的三波段并取得较高的反演精度［21］;Liu等基于Hyperion数据，确立了珠江入海口悬浮物浓度的波段组合模型［22］;李俊生等研究表明，CHRIS数据在内陆水质监测中具有巨大潜力［23－24］.5种传感器在400～850 nm之间的波段个数分别为8、12、102、60、54，实验结果表明，模拟数据的R2都遵循实验1的结果，稳定在0.85附近(图6).而MAPE体现出一些不同的特点，其中MODIS、Hyperion和HJ1－HSI数据都在实验1得到的曲线附近，三者遵循随波段数量减小，精度降低的规律;而MERIS数据和CHRIS数据明显分布在实验1中MAPE均值曲线之下，说明这两种传感器在理想状况下，能够通过主成分模型更好地对水体悬浮物浓度进行估算，特别是MERIS数据，虽然只有12个波段，却得到仅次于CHRIS数据的估算精度，说明MERIS传感器的波段设置包含了足够的水色要素信息，是主成分模型优秀的数据源.最后，除了MODIS数据以外，参与实验的另外4组模拟数据都能得到较为理想的估算精度，说明主成分建模方法在高光谱反演水体悬浮物浓度方面具有一定的适用性.

3 结论

本文针对传统经验模型不能充分利用高光谱信息，从而很难达到最佳拟合效果这一缺陷，通过建立主成分，达到利用较少分量综合反映水体信息的目的.研究表明，水体悬浮物浓度信息不仅包含在敏感波段遥感反射率(PC1)中，也包含在非敏感波段遥感反射率(PC2～PC6)中.

用前6个主成分构建多元线性回归模型，结果表明，相对于4种传统经验模型，主成分模型能够充分利用高光谱数据波段信息，受离群值影响较小，在拟合精度和估算精度方面均有大幅度提高.独立实验数据表明模型具有一定实用性.

通过两类实验，讨论了主成分模型的适用性，结果表明，在400～850 nm之间波段数量大于45的高光谱传感器都能用主成分模型得到高精度并且较稳定的估算模型.并且MERIS、HJ1－HSI、Hyperion和CHRIS这些常用的高光谱传感器的波段设置，都适合于主成分建模，其中MERIS数据虽然只有12个波段参与建模，但是其水色波段的设置，使得较少的波段也能获得较高的模型精度.

［1］周 艺，周伟奇，王世新等.遥感技术在内陆水体水质监测中的应用.水科学进展，2004，15(3):312－317.

［2］疏小舟，尹 球，匡定波等.内陆水体藻类叶绿素浓度与反射光谱特征的关系.遥感学报，2000，4(1):41－45.

［3］汪小钦，王钦敏，邬群勇等.遥感在悬浮物浓度提取中的应用——以福建闽江口为例.遥感学报，2003，7(1):54－57.

［4］Gin KY，Koh ST.Spectral irradiance profiles of suspended marine clay for the estimation of suspended sediment concentration in trophical waters.International Journal of Remote Sensing，2003，24(16):3235－3245.

［5］Härmä P，Vepsäläinen J，Hannonen T et al.Detection of water quality using simulated satellite data and semi－empirical algorithms in Finland.Science of the Total Environment，2001，268(1):107－121.

［6］Ahn YH，Moon JE，Gallegos S.Development of suspended particulate matter algorithms for ocean color remote sensing.Korean Journal of Remote Sensing，2001，17(4):285－295.

［7］刘堂友，匡定波，尹 球.湖泊藻类叶绿素a和悬浮物浓度高光谱定量遥感模型研究.红外与毫米波学报，2004，23(1):11－15.

［8］吕 恒，李新国，江 南.基于反射光谱和模拟MERIS数据的太湖悬浮物定量模型.湖泊科学，2005，17(2):104－109.

［9］李素菊，王学军.巢湖水体悬浮物含量与光谱反射率的关系.城市环境与城市生态，2003，16(6):66－68.

［10］Malthus TJ，Dekker AG.First derivative indices for the remote sensing of inland water quality using high spectral resolution reflectance.Environment International，1995，21(2):221－232.

［11］张恒喜，郭基联，朱家元等.小样本多元数据分析方法及应用.西安:西北工业大学出版社，2002.

［12］秦伯强，胡维平，陈伟民.太湖水环境演化过程与机理.北京:科学出版社，2004:1－296.

［13］唐军武，田国良，汪小勇等.水体光谱测量与分析Ⅰ:水面以上测量法.遥感学报，2004，8(1):37－45.

［14］唐军武.海洋光学特性模拟与遥感模型［学位论文］.北京:中国科学院遥感应用研究所，1999:107－110.

［15］Craig SE，Jones CT，Li WKW et al.Deriving optical metrics of coastal phytoplankton biomass from ocean colour.Remote Sensing of Environment，2012，119(16):72－83.

［16］韦玉春，王国祥，孙华芸.使用线性回归方法构建水体叶绿素a浓度高光谱估算模型的一个逻辑问题.数学的实践与认识，2010，40(18):100－110.

［17］刘 聪，汪 明.R软件在主成分分析中的应用研究.电脑知识与技术，2011，7(13):3092－3094.

［18］施 坤，李云梅，王 桥等.因子分析法在水质参数反演中的应用.湖泊科学，2010，22(3):391－399.

［19］刘忠华，李云梅，吕 恒等.基于偏最小二乘法的巢湖悬浮物浓度反演.湖泊科学，2011，23(3):357－365.

［20］Nechad B，Ruddick KG，Park Y.Calibration and validation of a generic multisensory algorithm for mapping of total suspended matter in turbid waters.Remote Sensing of Environment，2010，114(4):854－866.

［21］杨 煜，李云梅，王 桥等.基于环境一号卫星高光谱遥感数据的巢湖水体叶绿素a浓度反演.湖泊科学，2010，22(4):495－503.

［22］Liu DZ，Fu DY，Xu B et al.Estimation of total suspended matter in the Zhujiang(Pearl)River estuary from Hyperion imagery.Chinese Journal of Oceanology and Limnology，2012，30(1):16－21.

［23］李俊生，张 兵，申 茜等.航天成像光谱仪CHRIS在内陆水质监测中的应用.遥感技术与应用，2007，22(5):593－597.

［24］张 兵，申 茜，李俊生等.太湖水体3种典型水质参数的高光谱遥感反演.湖泊科学，2009，21(2):182－192.