基于H桥级联拓扑结构的中压电能质量扰动源研究

王碧芳，李 军

（武汉职业技术学院，湖北武汉 430074）

1 引言

随着电力电子技术的发展，在中高压配电网中广泛采用各种AC-AC、AC-DC-AC变频装置实现调速节能，此类装置在变频过程中可能给电网注入一些非整数次的间谐波电流。连接两个不同频率电网的换流装置，以及功率具有波动性的电弧炉等用电设备所产生电流也可能给电网注入更广泛的频谱分量［1］。这使得电网中谐波分布的情况越来越复杂。

由于非整数次谐波的出现，会给按照基于完整工频周期的各种功率定义、谐波计算及继电保护算法等带来较大的误差，因为有限个工频周期的采样数据可能不包含完整的非整数次谐波信息。该现象的出现将导致电能计量误差及电能质量分析结果偏差，同时也将影响各种基于传统工频理论的电力电子设备的功能效果和稳定性。这些影响已逐步引起研究人员的重视，并已开展了关于间谐波检测、间谐波产生机理及间谐波负荷模型等研究［1，2］。由于其频率的不确定性，给间谐波的研究带来很大的难度。从供电部门角度讲，通过构建能够发出各种电能质量功率信号的扰动源对计量、监测、保护及各种电力电子设备进行定性和定量的分析更具有实际意义。

本文基于H桥级联多电平电路，研究功能全面的电能质量扰动源拓扑结构及其控制策略。采用开关器件，使得扰动源具有功率密度高，自身损耗小，且易于实现大功率带载输出。

2 扰动源拓扑结构

基于全控型开关器件的变换电路，通常采用脉宽调制技术来实现任意波形的输出。受开关器件工作频率有限、死区时间及开关特性非线性等因素的影响，简单的两电平拓扑输出波形中难免会带有一些非特征分量，会给测试带来不必要的干扰。

如图1所示，采用H桥级联拓扑结构，可以提高等效开关频率和输出波形质量，也可以降低器件耐压水平，直接实现中高压输出，非常适合作为高压扰动源的拓扑。图1中每个功率单元为结构相同的H桥背靠背四象限变流器，可实现功率的双向流动。整流侧单元实现单位功率因数整流和直流电压控制，独立工作。逆变侧单元根据扰动源输出要求进行相应调制，并且与其余单元的逆变侧级联，通常级联的单元采用移相PWM调制，H桥中两个半桥的载波反相［3］。

扰动源按照输出性质可以分为电压型扰动源和电流型扰动源，电压型扰动源模拟电网某一供电节点，按照设定模拟各种电压波形输出。电流型扰动源模拟各种典型负荷，输出各种电流波形，注入给电网或用电设备。图1所示电路按照接线及控制方式的不同，可以实现两种模式。

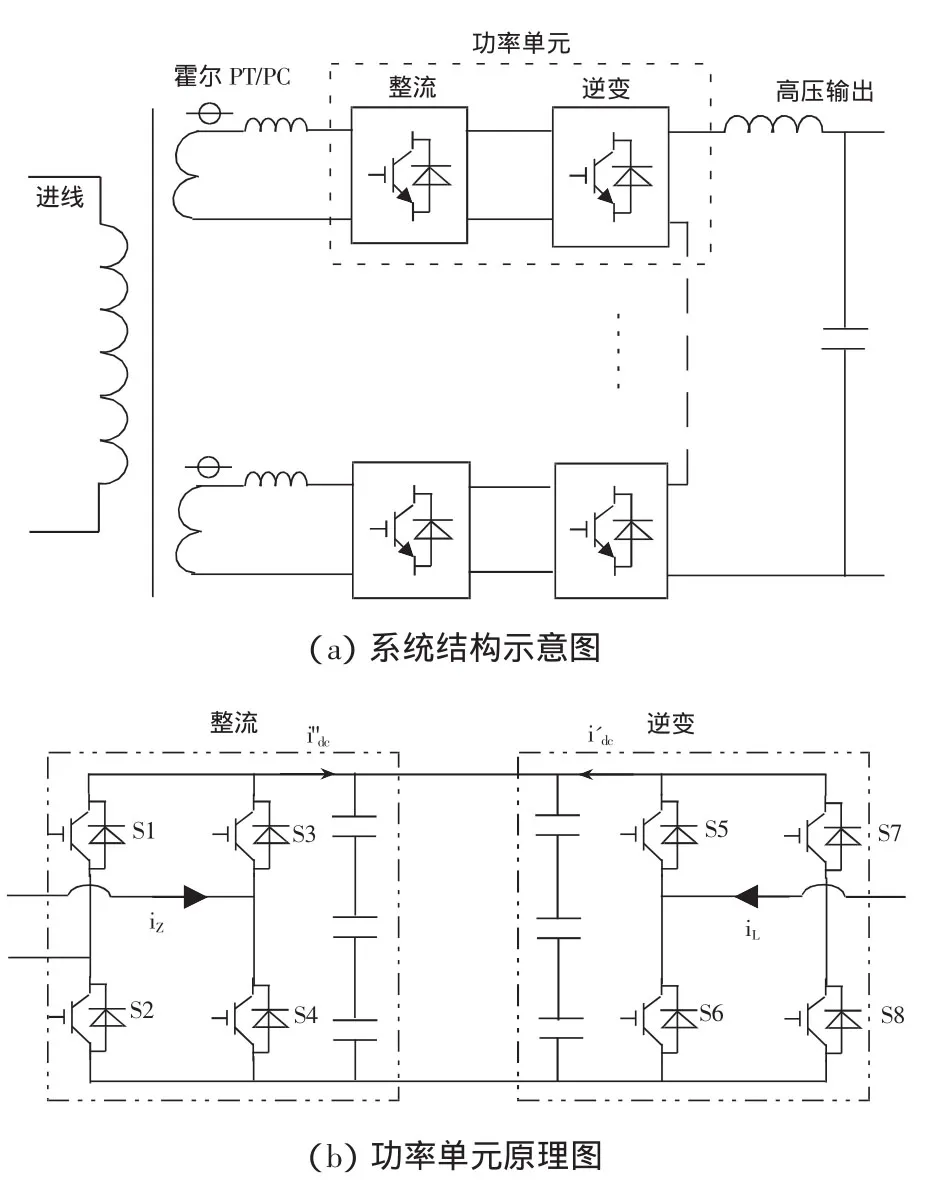
图1 H桥级联单相拓扑结构

采取该拓扑结构有两个难点：①输出谐波次数较高时，逆变单元为保证调制效果，需要较高的开关频率，会带来损耗增加的问题；②输出电流中含有非整数次谐波，尤其是频率接近工频的非整数次谐波时，直流电压的波动频率将不再是工频的整数倍，给直流电压控制带来问题。

3 逆变侧调制模式

单相H桥可以等效为两个共调制波但载波与反相的半桥串联，如图2所示为其调制波形示意图。为了达到较好的调制效果，调制波频率与载波频率必须满足。因此，输出波形的频率越高，要求载波频率即开关频率越高，开关器件的功耗会大大增加，给单元结构设计带来麻烦。

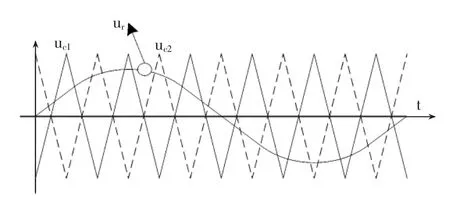
图2 H桥PWM调制示意图

H桥级联电路通常采取载波移相的方法来倍增等效开关频率，但仍然要求每个H桥的载波频率必须满足fc＞＞fr。因此，假定输出50次谐波，按照fc＞2fr关系来设计，开关频率至少要满足5kHz以上，才能保证叠加后的波形效果。而叠加后等效开关频率为2N×5kHz，其中N为每相串联的单元数，这个频率远远高于需输出的谐波频率。如果按照这种模式进行调制无法体现载波移相的优势，也会增加开关损耗。

对于级联电路，叠波调制也是一种方法。该方法在保证总体等效开关频率基础上，可以降低每个开关器件的开关次数。如图3所示，每个H桥载波峰-峰值为载波移相方式下的1／N，相位相同，但是幅值依次叠加。其中 uci+，uci-，i＝1…N 分别为两个半桥的载波。按照中模式调制，每个开关器件在一个调制波周期中只有的时间动作，其余时间保持固定开关状态［4］。如图4为采用叠波方法下，输出工频加上50次高频谐波的波形及其频谱。

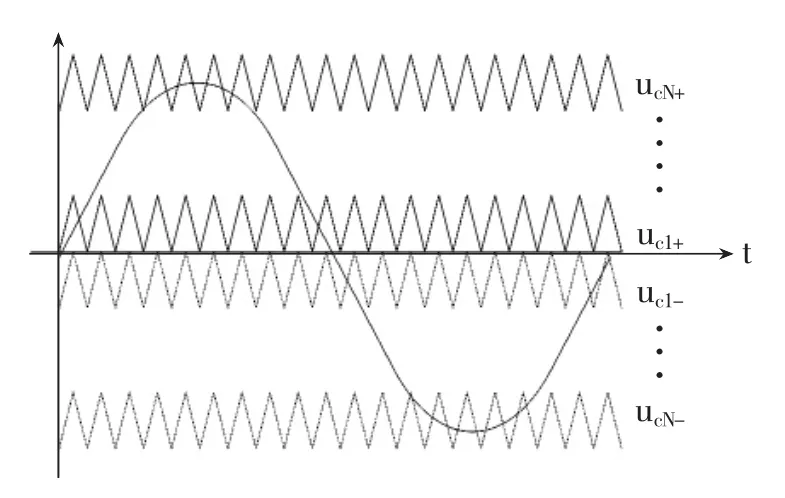
图3 叠波PWM调制示意图

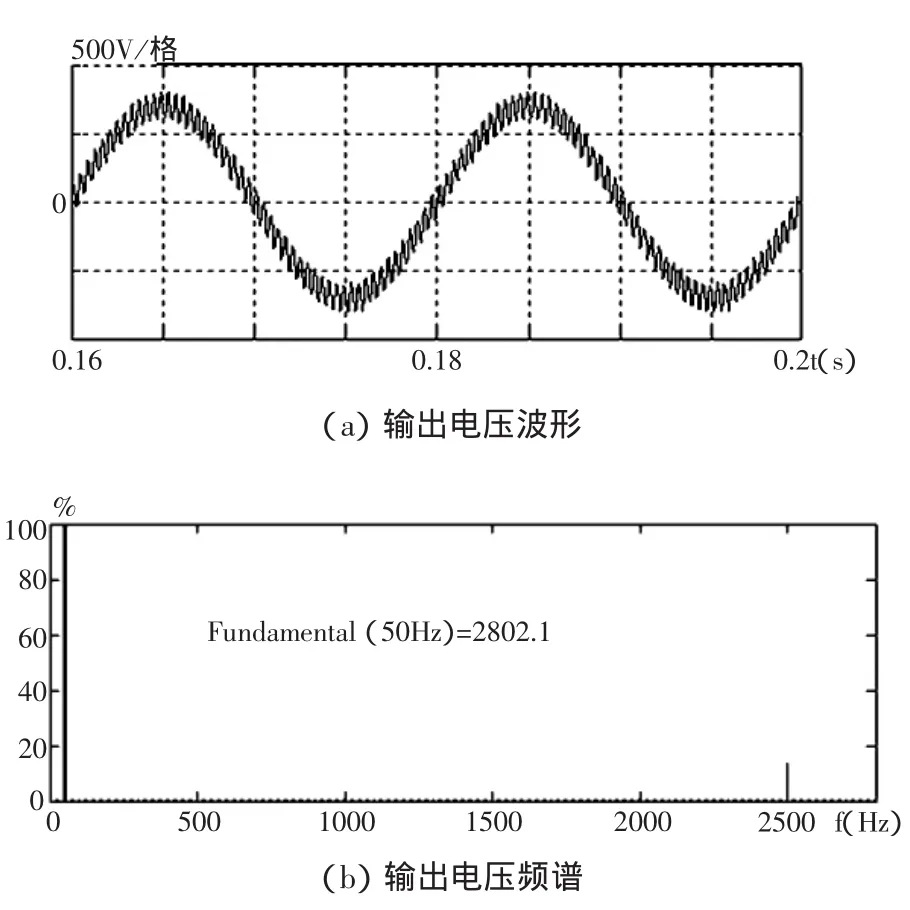
图4 基波加50次谐波调制效果

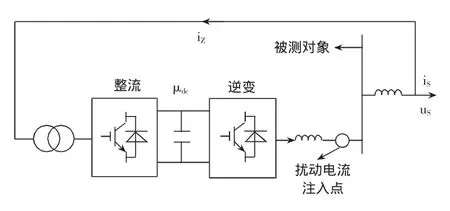
图5 电流扰动源模式系统等效示意图

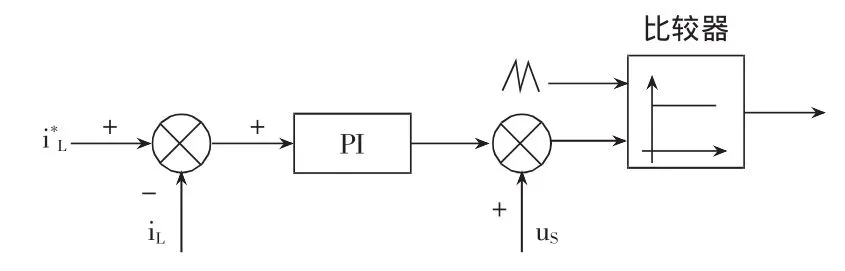
图6 逆变侧控制策略

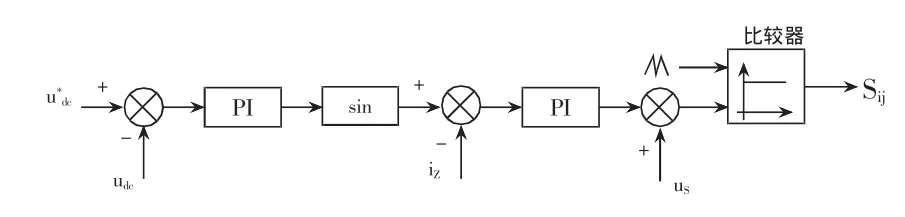
图7 整流侧控制策略

4 输出非整数次谐波时直压控制策略

如图5所示，电流扰动源模拟各种负载给电网注入任意电流，在扰动电流注入点进行测试。如图6所示，逆变侧采用电流控制策略确保注入电流逼进指令电流；如图7所示，整流侧采用直流电压控制及单位功率因数控制确保直流电容电压的平衡，同时实现单位功率因数。

如果电流扰动装置输出电流为某非整数次谐波如式（1），

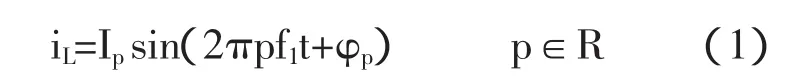
其中：p为谐波次数，是非整数；f1为基波频率。如图 1（b）所示有：

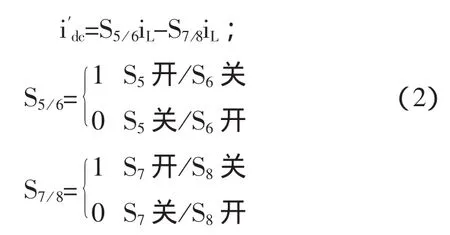
假定整流侧不工作，则：

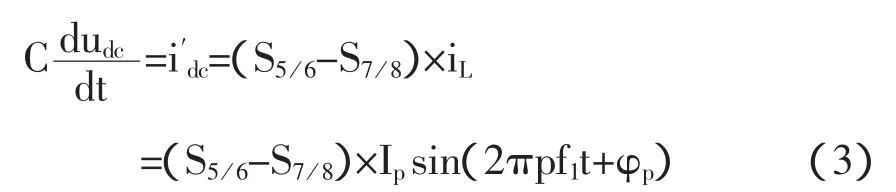
如图 6 所示，开关函数 S5／6与 S7／8为逆变器控制策略获得的调制电压与三角载波比较后获得。在高压系统中，调制电压中主要分量为系统电压us，则开关函数的频谱主要是调制电压中的基频，开关频率fc、以及2fc附近的一些频率分量。由于开关频率fc及2fc＞＞f1，对直流电压波动影响不大。因此在分析直流电压波动时可近似表示为：

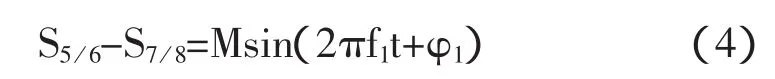
带入式（3）可得：

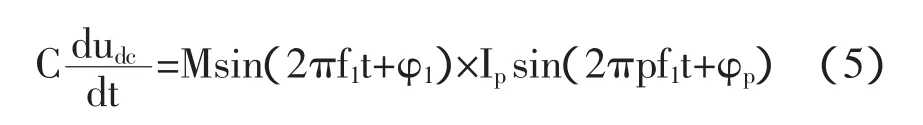
其中：M为调制比，经过变换后可得：

其中：Udc0为直流电压波动的直流分量，后面两项为直流电压的波动分量。当输出电流频率与工频接近，由于 p≈1，因此 1+p＞＞1-p，式中第二项波动幅度要小于第三项波动幅度。由此可知，直流电压中含有低频波动分量，波动频率与工频和非整数次谐波的频率差有关，两个频率越接近，波动幅度越大。

如图8所示，输出45Hz电流时直流电压波形及其频谱的仿真结果。可以看出，直流电压主要是一个5Hz的波动分量，由于波动频率低，且不是工频周波的整数倍，意味着逆变器与工频电源的功率交换周期不是工频的整数倍。而单位功率因数整流控制方法，是以每个工频周期的直流电压平均值为控制目标，通过控制电流为一有功电流来维持直流电压平均值平衡，直流电压瞬时值的波动靠电容来平衡。显然在图8所示的工况下，控制效果较差，如不采取其它控制策略只有依靠加大电容容量来限制直流电压的波动。

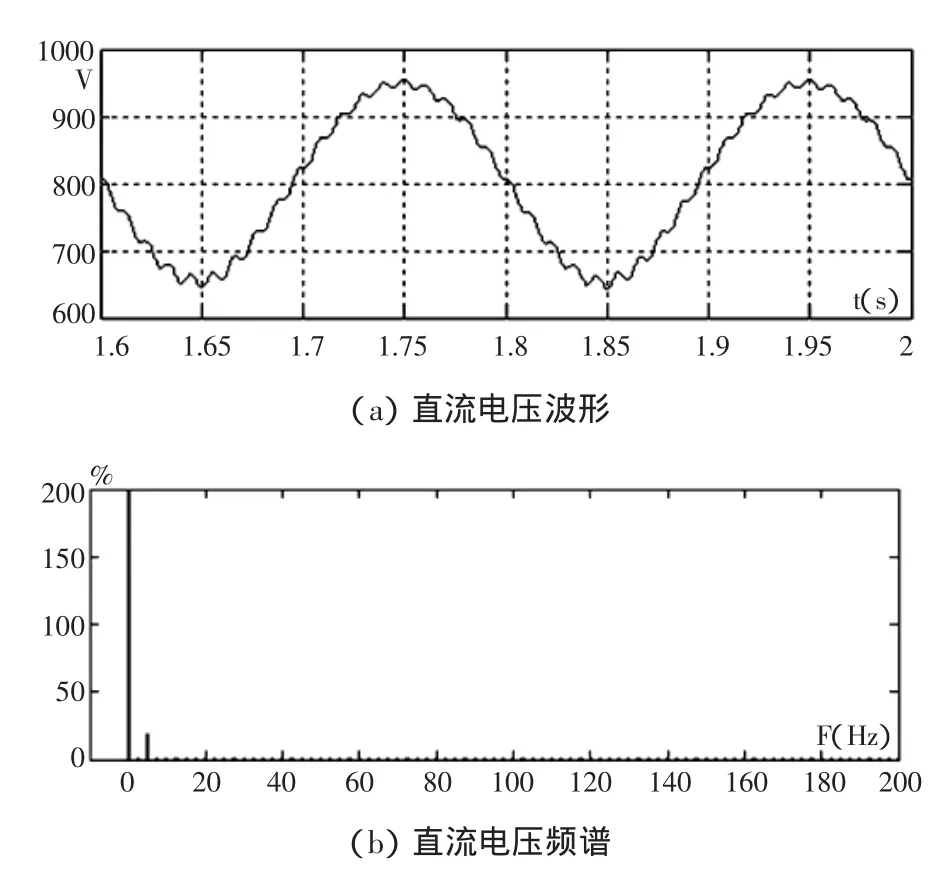
图8 输出45Hz电流时直流电压波形及频谱

分析直流电压变化时只考虑了逆变侧电流，如图5所示，实际上整流侧电流随着整流开关管的作用也会对直流电压波动产生影响，分析方法类似。作为电源扰动发生装置，在实现扰动电流输出目标的前提下，应尽量减小对电网的影响，因此可以考虑在整流侧也输出一个相反的非整数次谐波电流，一方面可以减小注入电网中的谐波，另一方面可以平衡直流电压的波动。此时整流侧控制框图如图9所示，与原来相比加入了一个非整数次指令电流。如图10所示为整流侧加入相反指令电流后直流电压波形及其频谱的仿真波形，从图9中可以看出，直流电压波动基本平稳，消除了图8中的5Hz分量。

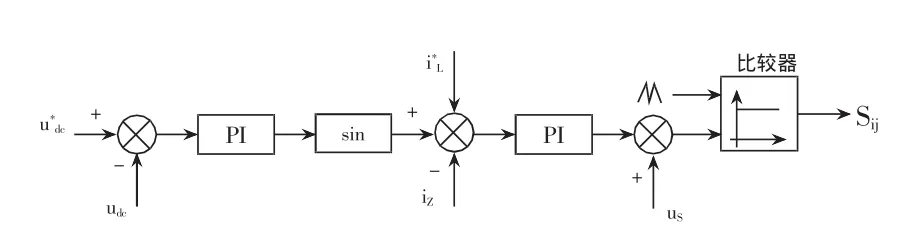
图9 改进后整流侧控制策略

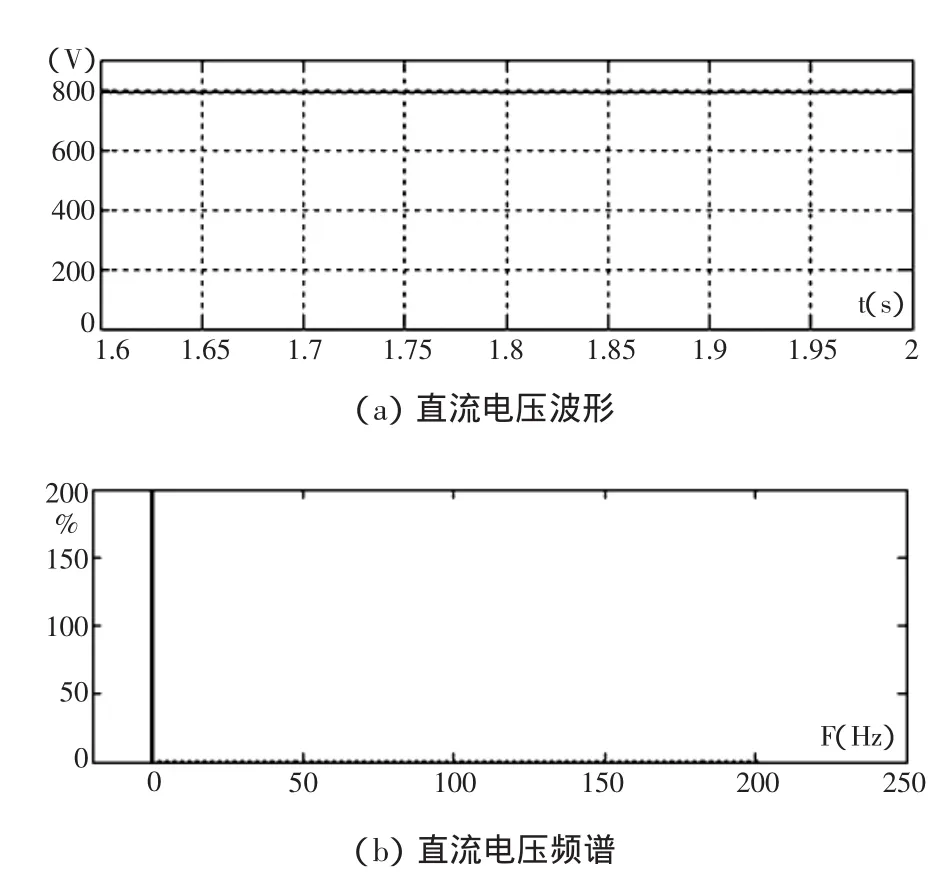
图10 输出45Hz电流时直流电压波形及频谱

5 结论

本文针对当前电网中出现的谐波频率及含量日益复杂的情况，研究了一种电能直流扰动源的拓扑结构，并针对该结构的两个关键问题提出了相应的控制策略：输出高次谐波时采用叠波PWM调制，在保证调制效果的同时，可以有效降低各单元的平均开关频率；逆变侧输出接近工频频率的非整数次谐波电流时，通过在整流侧控制环中加入一个相反的指令电流，不仅可以维持直流电压的平衡，还可以有效抑制对电网的扰动，给出的仿真结果验证了控制策略的正确性和有效性。

［1］杨洪耕，惠 锦，侯 鹏.电力系统谐波和间谐波监测方法综述［J］.电力系统及其自动化学报，2010，22（2）：65-69.

［2］李琼林，刘会金，张振环，陈红坤.基于互调原理的交直交变流系统中的间谐波分析［J］.中国电机工程学报，2007，27（34）：107-114.

［3］Tengfei Wang and Yongqiang Zhu.Analysis and Comparison of Multicarrier PWM Schemes Applied in H-bridge Cascaded Multi-level Inverters［J］.Industrial Electronics and Applications（ICIEA），2010 the 5th ieee conference on 2010 June 15-17：1379-1383.

［4］王碧芳，宫金武，胡 伟.级联型多电平逆变器的改进PWM 控制方法［J］.电力系统自动化，2006，30（7）：73-75.

［5］姚文熙，吕征宇，胡海兵.三电平H桥级联逆变器载波移相脉宽调制方式［J］.浙江大学学报（工学版），2008，42（8）：1330-1334.

［6］桂红云，姚文熙，吕征宇.DSP空间矢量控制三电平逆变器的研究［J］.电力系统自动化，2004，28（11）：62-65.

［7］吴洪洋，何湘宁.多电平载波PWM法与SVPWM法之间的本质联系及其应用［J］.中国电机工程学报，2002，22（5）：10-15.

［8］陈远华，刘文华，宋 强.基于FPGA的级联逆变器直接PWM 发生器［J］.电力系统自动化，2006，30（9）：61-63.