高温-高含冰量冻土原位旁压蠕变试验

张 虎，张建明，苏 凯，刘世伟

中国科学院寒区旱区环境与工程研究所，兰州 730000

0 引言

冻土是一种对温度十分敏感且性质极不稳定的土体，由矿物颗粒、冰、水和气体四相体系组成，这种特殊的、低温的和易变的地质体随着温度的变化会产生冻胀、融沉等现象，从而对冻土区建筑物的安全造成很大的危害[1-3]。高温冻土由于处于冰-水剧烈相变区，所以其物理力学性质很不稳定，具有未冻水含量高、强度小、压缩性大、对温度的变化非常敏感等特点[4-6]。在青藏高原多年冻土区，高温冻土的分布非常广泛[7]。近年来随着该地区工程活动的不断增加，对高温冻土尤其是高温-高含冰量冻土物理力学性质的深入研究也变得越来越重要。

旁压仪作为一种方便操作的原位试验装置，在冻土领域已经取得了非常广泛的应用[8-9]。利用旁压仪可以测得冻土的应力应变曲线[8]，从而得到冻土的蠕变变形性质。Ladanyi[10]在冻土区开展了大量的旁压蠕变试验后提出了一种幂函数的模型来描述旁压试验的初始蠕变阶段。Murat等[11]采用这种幂函数模型分析了海冰中旁压蠕变试验结果，并对此模型进行了改进；马小杰等[12]在青藏高原地区开展了短期旁压蠕变试验，采用此模型进行了参数反演，并分析了模型参数与影响因素之间的关系。但是上述模型主要应用于初始蠕变阶段所占比例较大的情形，而在稳定蠕变应变远大于瞬时应变和初始蠕变应变的情况下，一般采用线性两阶段模型来处理试验结果[13]，Ladanyi[14]将这种简单的方法发展为工程蠕变理论来解决地基承载力问题。

笔者利用旁压仪在青藏高原地区进行了原位旁压蠕变试验，并借鉴Ladanyi提出的工程蠕变理论对试验结果进行了分析，研究结果可为高温冻土区建筑物地基沉降计算提供参考。

1 试验场地

1.1 场地介绍

试验场地位于青藏高原腹地风火山北坡的北麓河盆地，见图1。此地平均海拔4618m，寒冷干旱，年平均气温为-3.8℃，极端最高气温23.2℃，极端最低气温-37.7℃[15]。该地区地表平坦、植被稀疏，表面多粉砂，附近多热融湖塘。据试验前钻探资料显示，该场地多年冻土厚度大于15.0m，天然上限深度一般为2.5～3.0m，上限以下3.0～3.5 m范围内地下冰较发育，冻土年平均地温为-0.3～-1.2℃，属高温不稳定多年冻土区。

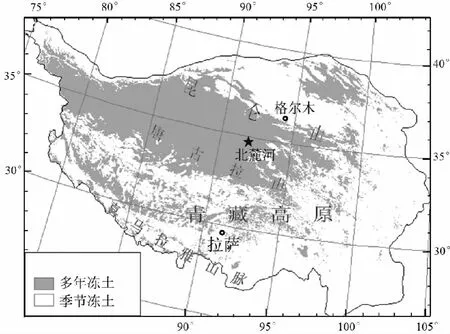
图1 试验场地位置Fig.1 Test site location

图2 试验点分布Fig.2 Test points distribution

1.2 试验点冻土条件

各旁压蠕变试验点位置如图2所示。根据该场地地温分布资料试验点分布在2个地点，试验点3-1-3-5分布在年平均地温稍高的位置，试验点3-6-3-8分布在年平均地温稍低的位置。其中，试验点3-2和3-3、试验点3-4和3-5、试验点3-6、3-7和3-8均分别位于同一个试验孔的不同深度。由于各个试验孔之间的距离至少为5m，所以可以认为各试验点之间不会相互干扰。温度是影响冻土力学性质的最主要因素之一，在现场旁压试验时，将温度探头黏附在旁压探头上以便得到试验点处冻土的具体温度。除了温度外，含水量也是影响冻土力学性质的主要因素之一。在钻取试验孔时将试验深度处的冻土取样烘干，然后测量冻土的含水量。所有试验点的深度、土质、温度和含水量见表1。由表1看出：本组试验的土质均为黏土；试验深度范围为2.6～6.4m，平均深度为4.8m；试验点温度范围为-1.20～-0.23℃，平均值为-0.57℃；含水量范围为15.9%～73.4%，平均值为31.6%。从冻土的条件来看，旁压试验结果能够反映高温-高含冰量冻土的特征。

2 试验仪器与操作

2.1 试验仪器

试验中所用的旁压仪为Menard预钻式旁压仪，试验时首先在土中钻一竖向钻孔，再将旁压探头下放到孔内试验深度进行旁压试验。旁压仪由3部分组成（图3）：G型旁压探头、压力控制系统（包括体变管、压力控制板和压力表）和压力源。仪器的工作原理是由外部压力源提供压力，然后利用压力控制系统调节由液体介质传递到旁压探头的压力值，从而使得孔壁在压力下水平扩张。为了防止仪器中的液体在试验过程中发生冻结，传压介质采用稀释了一半的防冻液。

2.2 试验操作

本组旁压蠕变试验共有8个，均采用等压力的加载形式，加载等级均为0.15MPa。每次加载后均持续60min，然后进行下一次加载。加载期间每隔1～5min记录一次压力和变形。当旁压仪体积读数达到750cm3时停止试验。

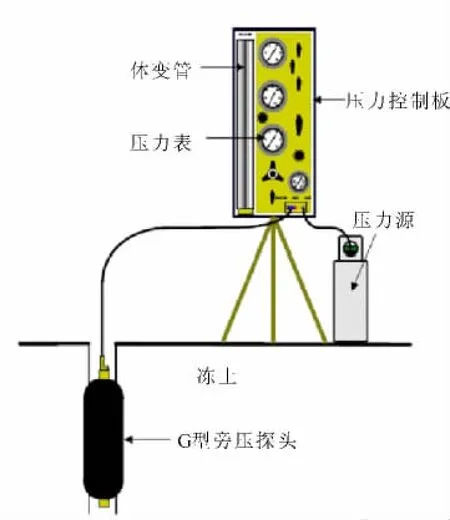
图3 旁压仪装置Fig.3 Schematic drawing of pressuremeter

3 试验结果

在旁压蠕变试验过程中，冻土在荷载作用下首先发生瞬时变形，然后发生蠕变，见图4。观察发现，在试验开始后，首级压力下的瞬时应变在总应变中所占的比例很大，之后每级压力下的瞬时应变相对小得多。这说明钻孔过程导致孔壁周围原始地应力的释放，使得冻土结构产生了一定的改变，当试验压力达到冻土的原始地应力水平时，冻土的结构才基本恢复。所以在分析试验结果时，一般是从第2级压力开始的。瞬时变形之后随着时间的延长应变过程进入第Ⅰ蠕变阶段（初始蠕变阶段）和第Ⅱ蠕变阶段（稳定蠕变阶段）。

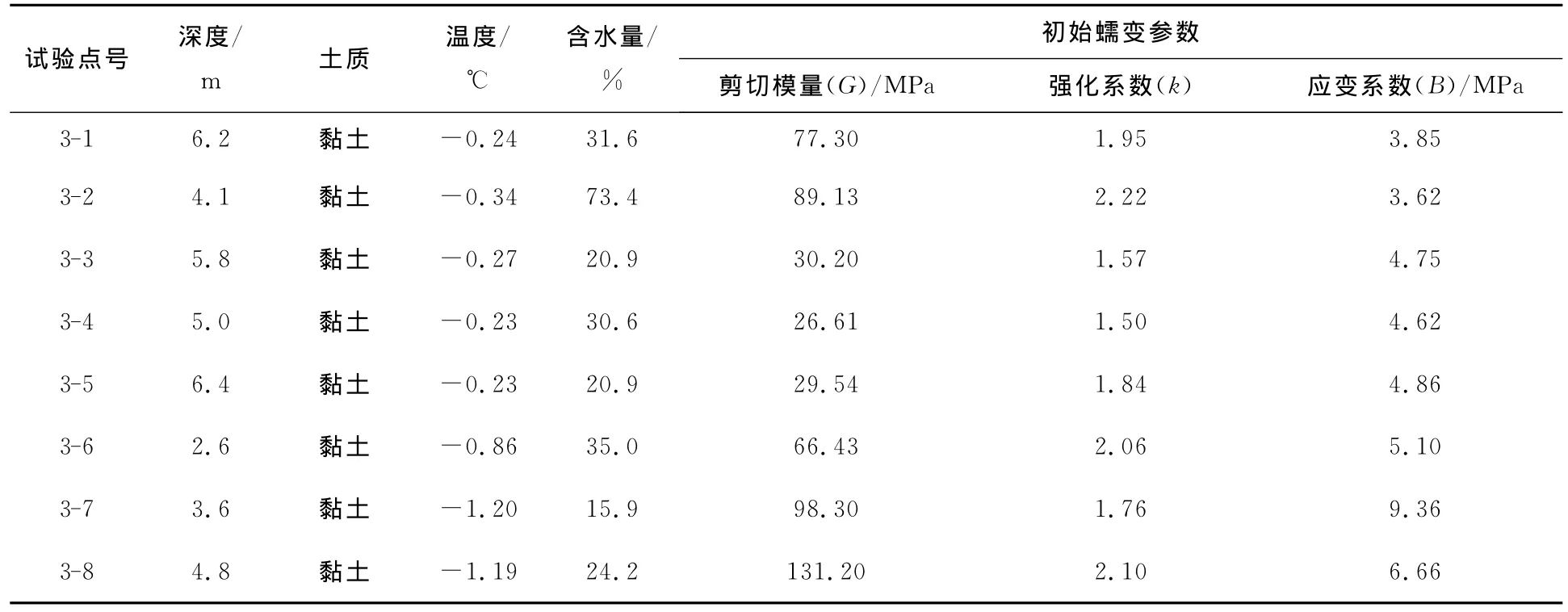
表1 试验点冻土条件及试验结果Table1 Conditions of the permafrost and test results

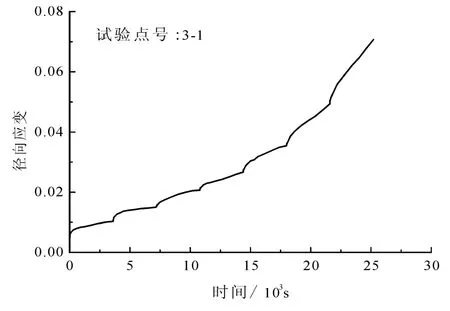
图4 旁压试验分级加载下的应变-时间曲线Fig.4 Strain-time curve under step lading in pressuremotertest

由文献[13]和[16]可知，若稳定蠕变阶段的持续时间和程度明显超过初始蠕变阶段，那么蠕变总应变可以由线性两阶段理论来表示。在该理论中，将瞬时弹性应变和初始蠕变应变合并看成伪瞬时应变εi，而将稳定蠕变阶段当作蠕变速率保持恒定的直线（图5），即

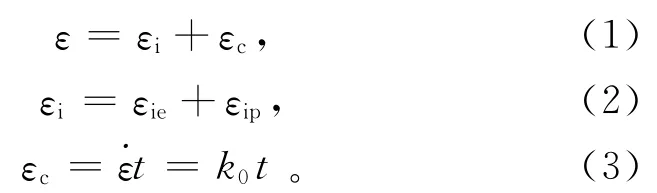
式中：ε为旁压总应变，指孔洞半径变化量（Δr）与孔洞初始半径（r0）之比；εc为稳定蠕变应变；εie为瞬时弹性应变；εip为初始蠕变应变为稳定蠕变速率；t为时间；k0为稳定蠕变阶段的应变速率。Ladanyi[14]在此方法的基础上提出了冻土的工程蠕变理论，证明了式（1）、（2）、（3）针对冻土工程问题时进行蠕变计算的正确性。工程蠕变理论将冻土复杂的蠕变问题变得相对简单，而且实验参数也相对较少。通过这种方法得到的计算结果在初始蠕变阶段与实际情况会出现偏差，不过这种偏差会随着蠕变的发展逐渐减小。由图4可以看出，在旁压试验中每级压力下的蠕变都没有出现渐进流动阶段，而稳定蠕变阶段均以恒定蠕变速率的形式在变化，而且稳定蠕变阶段的持续时间和程度明显超过初始蠕变阶段，所以可以借鉴Ladanyi的工程蠕变理论来描述旁压蠕变曲线。

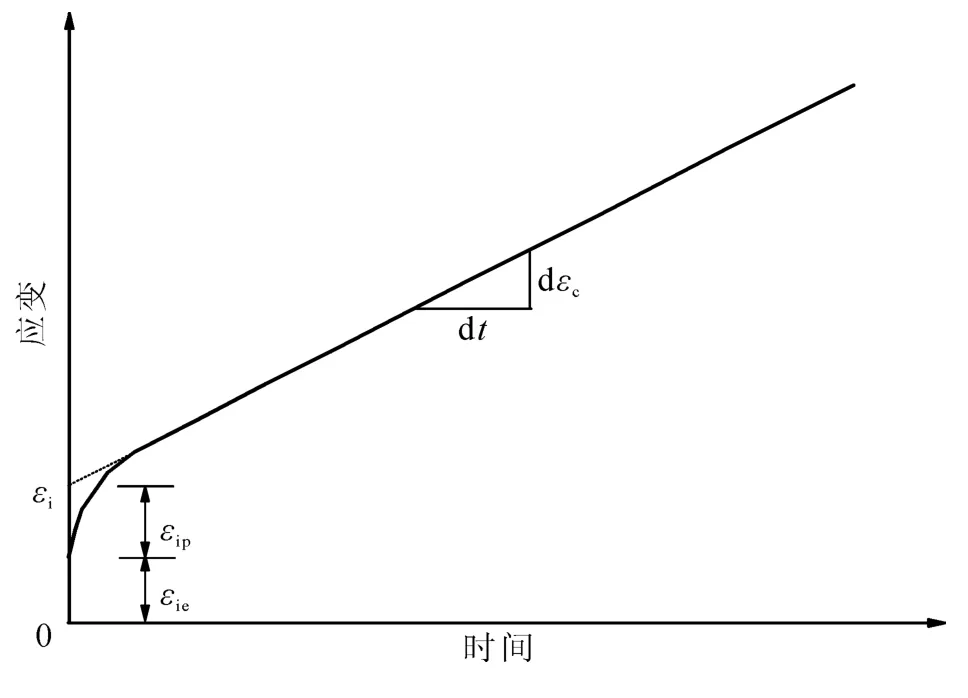
图5 蠕变过程中Ⅰ、Ⅱ阶段的线性近似曲线Fig.5 Linearized creep curve of stageⅠandⅡ

3.1 瞬时应变

蠕变试验的伪瞬时应变包括瞬时弹性应变和初始蠕变应变2部分。根据弹性力学，瞬时弹性应变可以写成

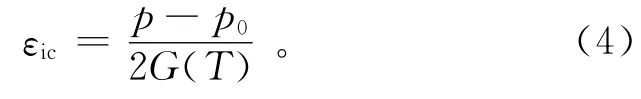
式中：p为孔壁所受的压力（MPa）；p0为原始水平地应力（MPa）；G为冻土的剪切模量（MPa），与温度有关；T为温度（℃）。在分析瞬时弹性变形时，所考虑的是孔壁周围冻土所受的累加压力以及在各级压力下的累加瞬时弹性应变，对初始蠕变应变亦然。在压力较小时，瞬时弹性应变在此压力下的总应变中所占的比例较大，随着压力的增加此比例在逐渐减小（图6）。在温度相同时该比例随含水量的增大而减小，在含水量相同时该比例随温度的升高而增大[12]。通过对所有旁压蠕变试验瞬时弹性应变分析发现：每个试验中瞬时弹性应变在各级压力下的总应变中所占比例的平均值为3%～7%。

图7为旁压蠕变试验中随着压力的增加，冻土剪切模量的变化趋势。由图7可知：当压力较小时，冻土虽然发生变形，但是结构没有发生破坏，所以剪切模量基本保持不变；当压力逐渐增大，冻土的结构发生破坏后，相应地其承受压力的能力迅速下降，导致剪切模量迅速下降。但是由于瞬时弹性应变在总应变中所占的比例很小，所以可以将各级压力下冻土的剪切模量平均后作为此冻土条件下的剪切模量。各旁压试验所得到的平均剪切模量见表1，其变化范围为26.61～131.20MPa，平均值为66.8 MPa。从表1可以看出，剪切模量与温度密切相关，除个别点较为离散外，剪切模量整体上随着温度的降低而呈线性增加，这说明对于高温冻土，温度的轻微改变都会引起剪切模量的大幅变化。

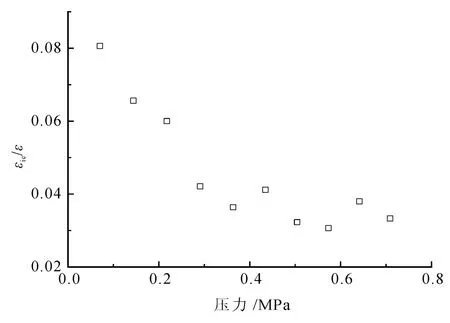
图6 每级压力下瞬时弹性应变在此级总应变中所占比例与压力的关系Fig.6 Elastic strain-total strain ratio under each pressure vary with pressure

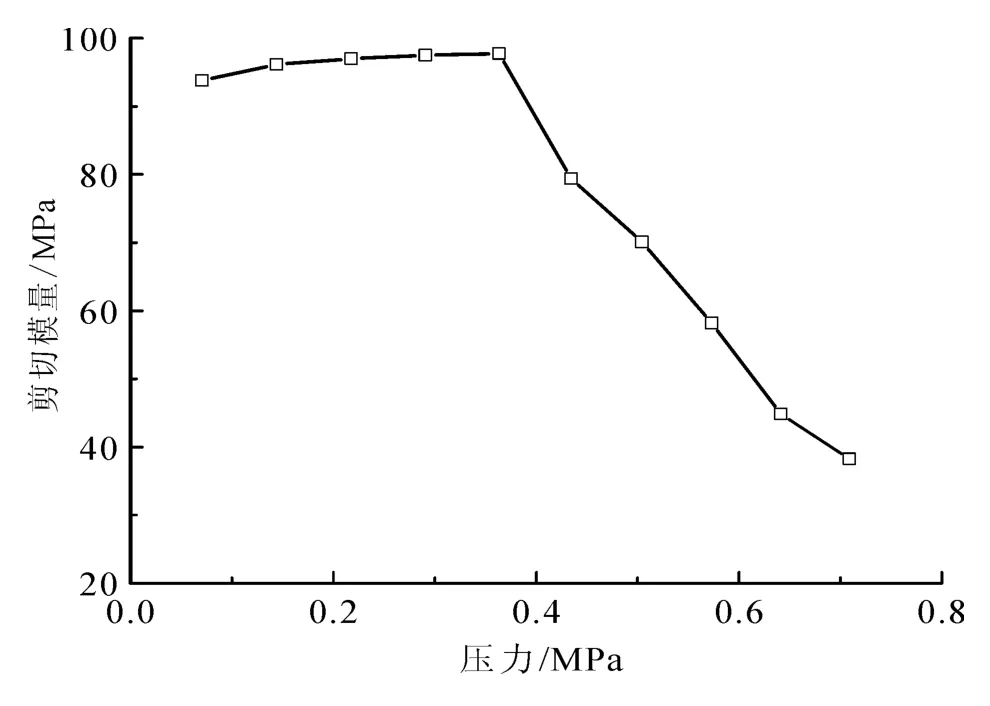
图7 剪切模量随压力的变化Fig.7 Variation of shear modulus with pressure

初始蠕变应变可以采用幂函数公式[5]来计算：

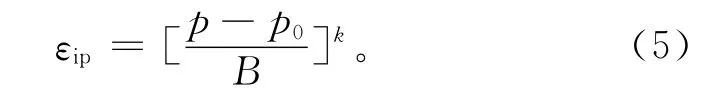
式中：B为应变系数（MPa）；k为强化系数。针对各级压力的蠕变曲线，笔者观察发现，将瞬时弹性应变开始到5min之间的应变当作初始蠕变应变是合适的。经过曲线回归后得到各旁压试验的参数k和B，列于表1中。强化系数k与土的类型有关，对于同一种土可取为常数，与土温和荷载作用时间关系不大。由于本组旁压试验遇到的土质均为黏土，那么强化系数的取值可取平均值k＝1.87，此值与马小杰[17]进行的冻结黏土单轴蠕变试验所得结果非常接近。应变系数B与冻土温度和荷载作用时间有关。由于笔者关注的是每级压力下初始蠕变的变形量，而非变形过程，所以可以认为若土温不变则B不变，即B只与温度有关。从图8可以看出，在整体趋势上参数B与温度之间呈现线性关系，温度越低，参数B的数值越大。

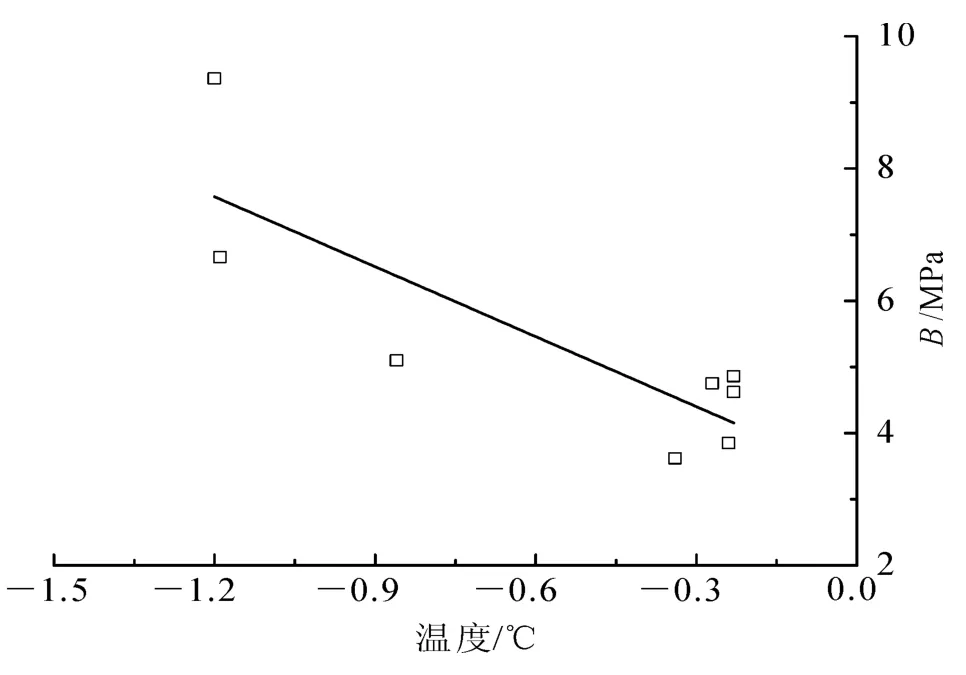
图8 参数B与温度之间的关系Fig.8 Relationship between Band temperature

3.2 稳定蠕变应变

Glen蠕变模型[18]无论是针对室内试验还是原位试验都得到了广泛的认可和应用[19-20]，因此稳定应变速率与压力的关系可以利用Glen蠕变模型来表示（图9）：

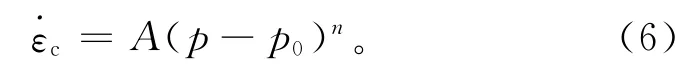
利用式（6）对旁压蠕变试验结果进行回归，得到了各个试验的模型参数值，见表2。参数n的变化范围为1.59～3.26。显然参数n与体积含冰量之间总体呈现一种线性关系，如图10，其表达式为

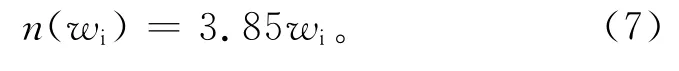
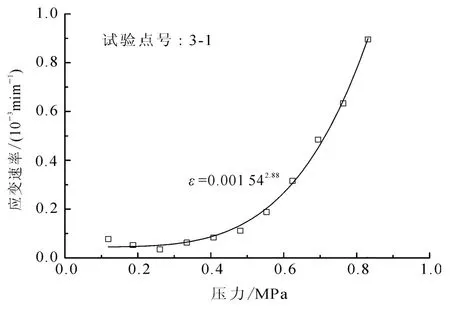
图9 应变速率与压力之间的幂函数关系Fig.9 Power law relationship between strain rate and pressure

式中，wi为冻土的体积含冰量。在本研究中，野外试验时测量的是质量含水量，为了便于和前人结果进行对比，本文根据质量含水量计算出体积含冰量（黏土矿物颗粒的密度取为2.71g／cm3），见表2。冻土的体积含冰量越高，n值越大，若冻土的体积含冰量外推至100% （纯冰），n＝3.85，这与Kjartanson[19]针对多晶冰开展旁压试验得出的n＝3.76是非常接近的。一些研究者通过室内试验认为，n与体积含冰量呈近似线性相关，体积含冰量越高，n值越接近于3.00[21]，对于纯冰而言，n＝3.00是被普遍认可的[21-23]。本文所得结果与室内试验结果有着较大差异，这说明试验方式的不同会引起试验结果的较大差异。

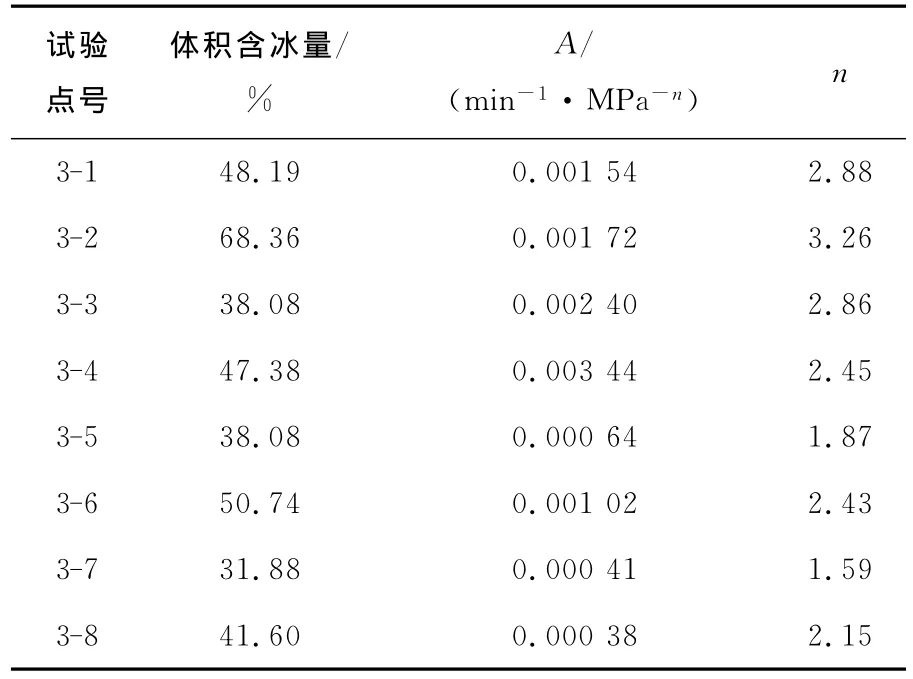
表2 稳定蠕变阶段流变参数Table2 Steady stage creep results

从系数A与温度的关系（图11）可以看出，A与负温的绝对值呈反比关系：温度越低，A值越小。在压力不变的情况下，温度与冻土蠕变速率的关系为：温度较低时，冻土中未冻水含量较低，冻土各成分之间的胶结力较大，使得蠕变速率变小；而当温度逐渐接近0℃时，冻土中的未冻水含量急剧增加，相应地冻土各成分之间的胶结力迅速减小，使得蠕变速率迅速增大。

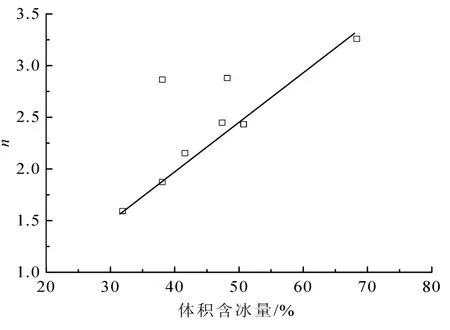
图10 参数n与体积含冰量的关系Fig.10 Vatiation of n with volumetric ice content

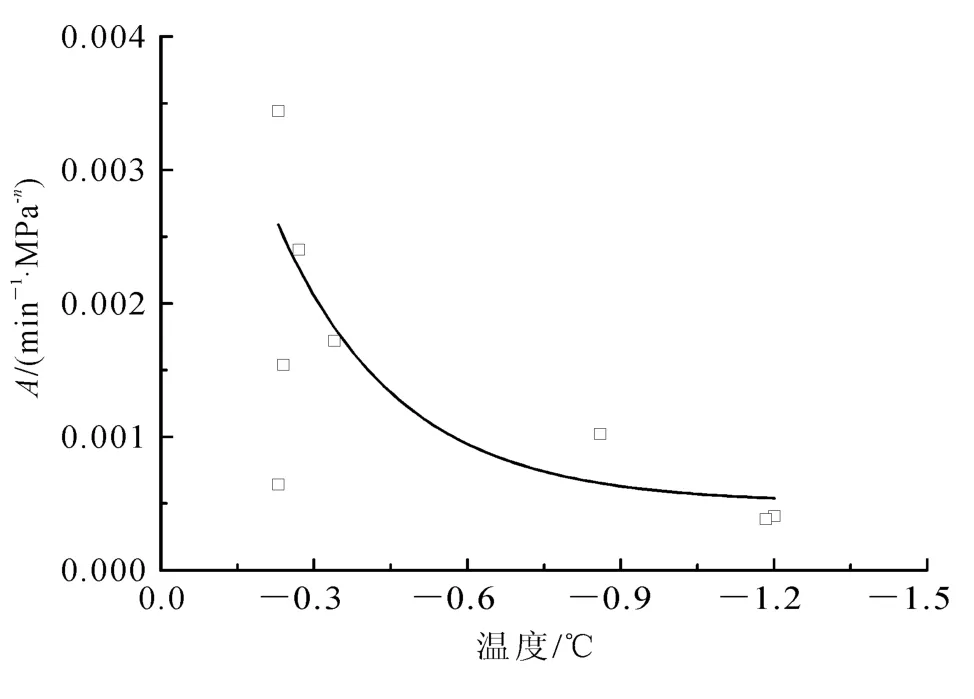
图11 参数A与温度的关系Fig.11 Vatiation of Awith temperature

4 讨论

根据旁压蠕变试验数据，文中采用的工程蠕变理论来描述冻土蠕变变形过程是一种简单、便于工程应用的变形计算方法。从试验结果分析中可以看出，初始蠕变变形所占比例很小，当冻土变形经历较长的时间时，初始蠕变变形可以忽略不计，甚至瞬时弹性变形也同样可以忽略。在温度不变或者变化不大的情况下，冻土的稳定蠕变变形被当作是以恒定的变形速率在发展，其随时间的变形量便为一条类似直线的曲线。图12表示的是青藏铁路北麓河段路基下多年冻土上限以下高温-高含冰量冻土层沉降变形过程曲线[24]。从图12可以看出，多年冻土的沉降量随时间的增加以一种几乎恒定的速率在发展，虽然期间受到温度影响，局部变形有所加快或减缓，但其总体趋势是不变的，而且经历了3年多的时间，仍没有出现衰减的趋势。综上所述，文中所采用蠕变理论与实际工程的沉降变形趋势是非常一致的，所以，应用该理论得到的计算结果可以为高温冻土区工程建设提供可信的参考。

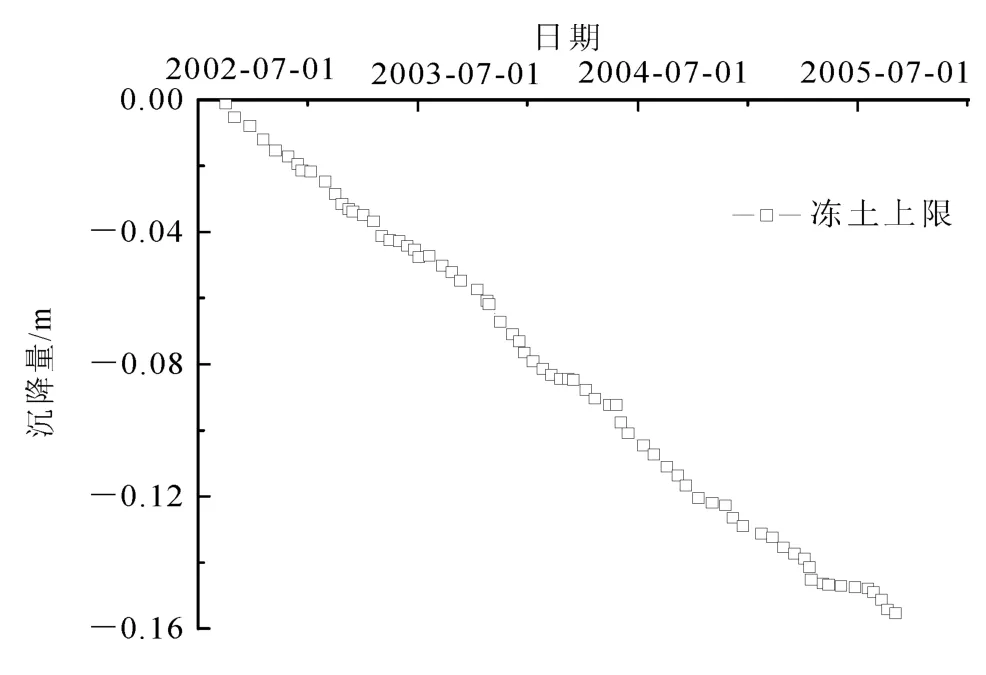
图12 路基下冻土的沉降过程曲线[24]Fig.12 Settlemet of permafrost under embankment[24]

5 结论

1）根据原位旁压试验结果，高温-高含冰量冻土的蠕变变形可采用Ladanyi所提出的工程蠕变理论来分析。在此理论的基础上，笔者将每个变形阶段的应变计算公式进行了改进，使得蠕变计算过程更加简单。经过公式拟合所得到的参数总体上与前人所得到的结果较为接近。文中所采用的冻土蠕变工程理论虽然不能严格地描述蠕变曲线的各个阶段，但也是一种满足工程应用的冻土蠕变计算方法，能够为高温冻土区地基沉降计算提供有力的支持。

2）利用旁压仪能够方便地开展针对冻土蠕变性质的原位试验。由于现场试验中冻土的地质条件复杂，随机性强，所以试验结果稍显离散，但是并不影响本文结论的得出。为了使试验参数更加准确，更方便于工程应用，在以后的研究中，还需要增加大量的原位旁压试验。

（References）：

[1]吴紫汪，刘永智.冻土地基与工程建筑[M].北京：海洋出版社，2005.Wu Ziwang，Liu Yongzhi.Frozen Subsoil and Engineering[M].Beijing：Ocean Press，2005.

[2]Wu Zhenhan，Patrick J B，Hu Daogong，et al.Migrating Pingos in the Permafrost Region of the Tibetan Plateau，China and Their Hazard Along the Golmud-Lhasa Railway[J].Engineering Geology，2005，79：267-287.

[3]Wu Zhenhan，Patrick J B，Wang Lianjie et al.Numerical Modeling of Stress and Strain Associated with Bending of an Oil Pipeline by a Migrating Pingo in the Permafrost Region of the Northern Tibetan Plateau[J].Engineering Geology，2008，96（1／2）：62-77.

[4]崔托维奇.冻土力学[M].张长庆，朱元林，译.北京：科学出版社，1985.Tsytovich H A.Mechanics of Frozen Soil[M].Translated by Zhang Changqing，Zhu Yuanlin.Beijing：Science Press，1985.

[5]维亚洛夫.冻土流变学[M].刘建坤，刘尧军，徐艳，译.北京：中国铁道出版社，2005.Vyalov C C.Rheology of Frozen Soil[M].Translated by Liu Jiankun，Liu Yaojun，Xu Yan.Beijing：China Railway Publishing House，2005.

[6]朱元林，刘永智，谢先德.青藏高原地下冰现场蠕变试验研究[C]／／青藏高原冻土研究论文集.北京：科学出版社，1983.Zhu Yuanlin，Liu Yongzhi，Xie Xiande.In-Situ Creep Test Research of Ground Ice on Qinghai-Tibet Plateau[C]／／Proceedings of the Permafrost Research on Qinghai-Tibet Plateau.Beijing：Science Press，1983：124-130.

[7]程国栋.青藏高原多年冻土区路基工程地质研究[J].第四纪研究，2003，23（2）：134-141.Cheng Guodong.Research on Engineering Geology of the Roadbed in Permafrost Regions of Qinghai-Xizang Plateau[J].Quaternary Sciences，2003，23（2）：134-141.

[8]Ladanyi B，Johnston G H.Evaluation of in Situ Creep Properties of Frozen Soils with the Pressuremeter[M].Ottawa：National Research Council Canada，1974.

[9]Shields D H，Domaschuk L，Man C S，et al.The Deformation Properties of Warm Permafrost[C]／／Chaney R C，Demars K R.Strength Testing of Marine Sediments：Laboratory and In-Situ Measurements.Philadelphia：American Society for Testing and Materials.1985：473-486.

[10]Ladanyi B.Interpretation of Pressuremeter Test Results in Frozen Soils[R].Ottawa：Internal Report No.401of the Division of Building Research，1972.

[11]Murat J R，Ladanyi B，Huneauit P.In Situ Determination of Creep Properties of Sea Ice with the Pressuremeter[J].Canadian Geotechnical Journal，1989，26：575-594.

[12]马小杰，张建明，郑波，等.青藏高原高温冻土旁压蠕变试验研究[J].中国铁道科学，2008，29（6）：1-5.Ma Xiaojie，Zhang Jianming，Zheng Bo，et al.Experimental Study on the Lateral Pressure Creep of Warm Permafrost in Qinghai-Tibet Plateau[J].China Railway Science，2008，29（6）：1-5.

[13]Hult J A.Creep in Engineering Structures[M].Blaisdell：Waltham Mass，1966.

[14]Ladanyi B.An Engineering Theory of Creep of Frozen Soils[J].Canadian Geotechnical Journal，1972，9：63-80.

[15]牛富俊，张建明，张钊.青藏铁路北麓河试验段冻土工程地质特征及评价[J].冰川冻土，2002，24（3）：264-269.Niu Fujun，Zhang Jianming，Zhang Zhao.Engineering Geological Characteristics and Evaluations of Permafrost in Beiluhe Testing Field of Qinghai-Tibetan Railway[J].Journal of Glaciolgy and Geocryology，2002，24（3）：264-269.

[16]Odqvist F K G.Mathematical Theory of Creep Rupture[M].London：Oxford University Press，1966.

[17]马小杰.高温-高含冰量冻土强度及蠕变特性研究[D].北京：中国科学院研究生院，2006.Ma Xiaojie.Study on Strength and Creep Characteristics of Warm and Ice-Rich Frozen Soil[D].Beijing：Graduated School of the Chinese Academy of Sciences，2006.

[18]Glen J W.The Creep of Polycrystalline Ice[J].Proceedings of the Royal Society of London：Series A，1955，228：519-538.

[19]Kjartanson B H，Shields D H，Domaschuk L，et al.The Creep of Ice Measured with the Pressuremeter[J].Canadian Geotechnical Journal，1988，25：250-261.

[20]Arenson L U，Springman S M.Mathematical Descriptions for the Behaviour of Ice-Rich Frozen Soils at Temperatures Close to 0℃[J].Canadian Geotechnical Journal，2005，42：431-442.

[21]Sinha N K.Constant Strain-Rate and Stress-Rate Compressive Strength of Columnar-Grained Ice[J].Journal of Materials Science，1982，17（3）：785-802.

[22]Cole D M.Strain-Rate and Grain-Size Effects in Ice[J].Journal of Glaciology，1987，33：274-280.

[23]Hooke R L，Mellor M，Budd W F，et al.Mechanical Properties of Polycrystallineice：An Assessment of Current Knowledge and Priorities for Research[J].Cold Regions Science and Technology，1980，3（4）：263-275.

[24]张建明，刘端，齐吉琳.青藏铁路冻土路基沉降变形预测[J].中国铁道科学，2007，28（3）：12-17.Zhang Jianming，Liu Duan，Qi Jilin.Estimation on the Settlement and Deformation of Embankment Along Qinghai-Tibet Railway in Permafrost Regions[J].China Railway Science，2007，28（3）：12-17.