崩塌落石产生涌浪的流固耦合运动分析

黄波林，王世昌，殷跃平，刘广宁，陈小婷

1.武汉地质调查中心，武汉 430205

2.中国地质大学工程学院，武汉 430074

3.中国地质环境监测院，北京 100081

0 引言

库区崩塌落石不仅对滚石运动路径上的物体存在威胁，而且入水后会产生涌浪，威胁航道安全。例如在瑞士的Lake Uri，由于1.6万 m3的危岩崩塌后会威胁下方公路和形成涌浪，1992年有关人员对其进行了爆破，苏黎世大学的水力学实验室（VAW laboratory）对涌浪进行了监测[1]。

落石运动过程十分复杂，受众多因素影响。如斜坡的微地貌、坡面的物质组成、落石的形态等条件都会影响落石的运动过程[2-4]。控制滚石动力学特征的主要参数是碰撞恢复系数[5]。秦志英等[6]、何思明等[7]、沈均等[8]、杨海清等[9]在理论上对碰撞恢复系数进行了分析。C.Mangwandi 等[10]、Rocscience[11]、A.Azzoni等[12]、R.W.Day[13]、章广成等[14]通过现场试验给出了碰撞恢复系数的建议值。目前有许多模拟落石碰撞过程的专业软件，如 CRSP[15]，Rocfall[11]，STONE[16]，CADMA[17]等。但这些软件只能计算滚石的运动特征，不能与流体耦合进行涌浪计算。

滚石以一定速度入水后会形成涌浪，滚石的几何形态与入水姿态都会对涌浪产生影响，具有强烈的三维特性。进行三维流体力学与固体力学耦合分析可获得从微观到宏观的直观结果，是目前涌浪研究的热点，也是未来研究的发展趋势。但由于软硬件制约，国内鲜有文献对此进行报导。在国外，B.H.Choi等[18]采用RANS系统进行了三维孤立波爬高分析；Silvia等[19]利用移动墙采用三维浅水波模型模拟了瓦伊昂滑坡涌浪事件；F.Montagna等[20]利用Flow-3D进行了三维海岛滑坡涌浪研究，并与物理试验进行对比分析；M.Pastor等[21]耦合三维SPH法和FEM法进行了几个灾难性滑坡涌浪的研究；Stéphane Abadie等[22]采用两相流的 N-S方程模拟研究了三维滑块入水产生的涌浪。国外的研究多集中在概化性三维滑块和典型滑坡涌浪实例上进行研究，尚无研究者对崩塌落石涌浪全过程进行流固耦合分析。

长江三峡库区风景秀丽、山高坡陡，是著名的旅游景点，也是崩塌落石的多发区。为给三峡库区巫峡剪刀峰一带危岩防治风险管理提供科学依据，笔者以三峡库区巫峡剪刀峰为原型，尝试在计算流体力学软件（computing fluid dynamic，CFD）中采用6自由度的运动碰撞模型（general moving objects collision model，GMO）耦合计算崩塌落石形成的涌浪效应，为类似崩塌落石涌浪研究提供借鉴。

1 剪刀峰斜坡概况

三峡库区巫峡剪刀峰位于重庆市巫山县长江北岸，巫山新县城下游16km。2006年至今的野外调查、巡查发现，剪刀峰一带区域崩塌落石现象时有发生。该区域斜坡位于神女溪-官渡口向斜北翼，由三叠系嘉陵江组三段（T1j3）灰岩构成同倾顺向坡，平均坡度超过50°。斜坡岩体剖面X节理发育，坡体被X节理和层面裂隙切割成菱形结构体。块体沿X节理和层面发生破坏，脱离母岩后向长江或两侧冲沟方向崩落。块体的体积较小，但是落石高差往往超过400m，势能巨大，对过往船只仍然构成较大威胁。由于沿X节理破坏，该区域形成了三角面和V型沟的典型山体地貌。

剪刀峰一带分别于2007年7月3日和7月23日发生过两次崩塌，两次崩塌的危岩源自同一地点。崩塌体呈板状，东西长20m，厚0.35m，高80m，体积560m3（图1）。7月23日第二次崩塌落石入江时，其下游50m处有一艘载有50余名乘客的客船正贴近悬崖往上游方向行使，所幸落石没有击中船只[23]。

图1 2007年剪刀峰发生崩塌后照片Fig.1 Jiandao Peak photo after rockfalling in 2007

该区域长约2.5km，坡高险峻，因为是著名的旅游景点，不适合进行大规模危岩清除或拦网防护等防治工作。该斜坡段无人居住，其主要危害对象为航道过往船只，危害的主要形式为落石打击和涌浪；因此有必要对落石及其产生的涌浪进行研究，为该区域的地质灾害防治及风险管理提供依据。

2 崩塌涌浪的流固耦合运动分析

库岸崩塌落石产生涌浪是一个很复杂的过程。首先，石块在陆地斜坡上进行滑动、弹跳；然后落入水体，石块在水体和水下斜坡中运动，与水体相互作用产生涌浪，出现涌浪传播。为了解决这一复杂的流固耦合运动问题，笔者在国内首次引入Flow-3D软件进行建模、分析。

2.1 Flow-3D介绍及耦合模型建立

Flow-3D是一款由Flow Sciences公司开发的通用流体动力学计算软件，始于1980年的Los Alamos National Laboratory。在物质守恒、动量守恒、能量守恒等欧拉方程框架内，Flow-3D采用了有限体积差分法逼近离散化计算域进行求解。该软件有大量的模型用于模拟相变、非牛顿流体、孔隙介质流、表面张力效应、两相流等。Flow-3D采用FAVOR （fractional area／volume obstacle representation）和 VOF（volume-of-fluid）技术来求解三维瞬时Navier-Stokes方程，能够提供极为真实且详尽的自由液面（free surface）流场信息。FAVOR和VOF技术使得在欧拉网格内能够定义固体边界，能够在计算流体响应固体边界时追踪流体边界。采用这一方法，固体物质独立生成网格，能够高效率且精确地定义几何外型。Flow-3D的FAVOR和VOF技术，使得它在描述自由液面流动方面具有独特的准确性和真实性[24]。

Flow-3D有许多不同的湍流模型用来模拟湍流，包括普朗特混合长度模型（Prandtl mixing length model）、k-ε 方 程 （k-ε model）、RNG 方 程（RNG scheme）和 LES模型（large eddy simulation model）。同时，在Flow-3D中有一个特殊的GMO碰撞计算模型[24]，能够提供使用者预测移动对象在流体内运动的状况。GMO模拟刚体运动，可以是指定运动方式或与流动耦合计算。指定运动方式时流动受物体运动影响，而物体运动不受流体影响。与流动耦合时物体运动和流动是动态耦合的（两者互相影响）。两种方式中运动物体都可以有6个自由度，计算时可以有多种类型的运动物体，且可以相互碰撞。碰撞分析可以选择采用弹性碰撞、部分塑性碰撞、完全塑性碰撞3种。弹性碰撞是指运动过程中运动物体间碰撞没有能量损失。完全塑性碰撞是指运动物体间碰撞后，能量完全损失掉，这一碰撞分析采用总体摩擦系数和总体碰撞恢复系数来控制。碰撞恢复系数处于0和1之间，0代表完全塑性 ，1代表完全弹性。笔者采用了k-ε方程和GMO模型的耦合模型进行分析计算。

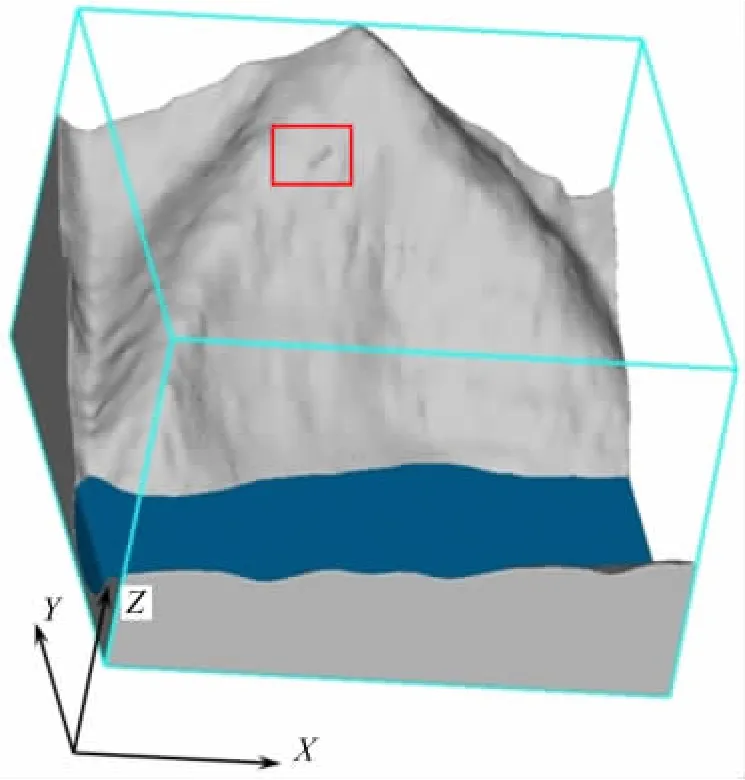
图2 耦合模型Fig.2 Coupling model map

以剪刀峰斜坡河谷为例（图2）建立了一个X方向1.6km长，Y方向1.5km宽，Z方向1km高的斜坡模型。根据调查分析，剪刀峰发生1万m3的崩塌落石概率较小。而涌浪与块体入水体积有密切的正相关性，假定剪刀峰发生1万m3落石入水，以计算可能的最大涌浪高度和风险。因此，建立了一个长80m，宽30m，厚5m的板状GMO岩体，其密度为2600kg／m3。这一假设的块体体积为1.2万m3，初始重心高度652m，初始状态为静止。根据章广成等[14]对灰岩区落石碰撞恢复系数的研究，计算采用的碰撞恢复系数为0.72，总体摩擦系数为0.57。采用5m的计算网格进行离散，共有1827万个网格单元。k-ε湍流模型边界条件为：X方向（河流动方向）为静水压力边界（定水头边界），Y方向为流出边界，Zmax方向为自由表面边界（水压力为0，空气界面），Zmin方向为不透水 Wall边界（隔水边界）。k-ε湍流模型初始条件为静止水面，水位为175m。GMO模型的边界条件为：Z方向为重力加速度，三维斜坡体为封闭边界（不可进入的区域），其他区域为开区域（可以进入的区域）。GMO模型的初始条件为静止状态。计算模拟板状岩体从剪刀峰处崩塌-滚动-弹跳-入水-涌浪的全过程，模拟时间设置为120s。

2.2 流固耦合运动结果分析

该耦合计算模型在LENOVO THINK工作站上计算约9h，形成了152Gb的结果数据文件。GMO运动过程模拟显示（图3），块体在陆地斜坡上经历了滑动、翻转、弹跳等运动。岩块从静止状况开始下落后，有3次较大的弹跳发生在陆地斜坡上，有1次弹跳是入水之后发生的。由于陆地斜坡陡峻，在陆地斜坡上岩块只有一小段进行了滑动或滚动，大部分是碰撞后弹跳飞过的。其运动轨迹显现三维性，并不是在一个平面上运动。由于未考虑空气阻力问题，运动过程中，岩块的能量损失主要来源于碰撞和滚动时的摩擦。

虽然每次碰撞弹跳都会造成总能量损失和速度的暂时降低（图4），但总体来看，随着岩块的下降，势能转化为动能，动能不断增加，速度不断增加。20 s左右速度达到最大，约80m／s，能量也达到最大，约9.30×1011J。20s后岩块入水，岩块入水是该过程的一个转折点。入水后，GMO的总能量开始持续下降（图4a），能量一部分传递给水体，一部分碰撞水下斜坡损失了。

岩块进入水体后，与水体相互作用，两者的运动相互影响。对岩块而言，入水后其运动方向与轨迹发生较大的变化，由开始南南东的斜向下运动方向为主，慢慢转化为东西方向摆动向下运动。瞬时过程图（图4b）显示为：在波浪和水的作用下，岩块在水中发生左右飘动下沉。运动速度图上显示为XY方向速度出现方向性摆动。岩块在陆地477m高差的斜坡上运动了20s，在水下140m高差斜坡运动了15～20s。这是由于流固耦合作用，流体让岩块不易停止沉底，岩块的水下运动时间明显延长。运动物体完全停止后，流体获得的总动能为6.08×1010J，与入水前岩块的总能量相比较，能量传递率约为6.54%。

流体和运动物体的相互作用，极大地消耗了运动物体的能量，改变了运动物体的原有运动韵律，延缓了运动固体的下沉时间，延长了流-固能量交换过程。这一流固耦合过程，由于能量交换时间过长而不利于涌浪形成。

岩块入水后，水体沿石块四周壁面向上涌起飞溅，激起了较大的水花（水舌），最大高度达到了15.60m，而后散落入水中。以入水点为圆点，开始形成一个新月半圆锥状的孤立涌浪波，在传播过程中形成最大涌浪波约10.0m，距离岸边约150.0 m。在涌浪的开始阶段，涌浪波形成一圈一圈的环状水波进行传播（图5a），衰减非常快。波的运动方向也为环状，直至环状波传播至对岸，波的运动方向才开始转为放射状沿河道上下游进行传播，同时反射波开始与涌浪波叠加（图5b）。波浪传播至河道中线（弘深线）时，波高衰减为2.40m。传播至对岸时，波高已衰减至0.89m左右，最大爬高为1.90 m。波浪沿河道传播500.0m后的最大浪高为1.50 m左右，1km外降低至1.0m以下。

借鉴国家海洋局2009年11月发布的《风暴潮、海浪、海啸和海冰灾害应急预案》对计算区域航道进行涌浪风险预警分区：当波浪大于3m时为航道红色预警区；当波浪为2～3m时为航道橙色预警区；当波浪为1～2m时为航道黄色预警区；当波浪小于1m时为蓝色预警区。根据这一标准，在入水区附近（离岸200m内）为航道红色预警区，在离剪刀峰岸线200～350m时为航道橙色预警区，在离剪刀峰岸线350m后的航道为黄色预警区。因此，河道中心线以南（上行航道）的涌浪较小，风险较低。

另外，笔者采用的崩塌落石为1.2万m3，实际崩塌如此大方量的可能性较低，产生的涌浪高度也将比本文所得结果低，预警等级相应会降低。因此，如果将目前全河面航道的北航道往南移350m左右，将红色-橙色预警区河面作为避让区，则航道内的涌浪预警将从红色预警区降为黄色或蓝色预警区，涌浪风险大大降低，航道安全度将得到提高。

3 讨论

通过对崩塌落石涌浪案例的流固耦合分析研究，发现有以下问题值得探讨和思考：

1）就目前PC机硬件而言，小的GMO体意味着更小的离散网格和更多的网格单元。上千万或上亿的网格单元常常会导致一些PC机硬件无法满足计算要求；即便是可以满足，其所需的计算时间也是很漫长的。这也是笔者没有采用更小尺寸落石块体的重要原因之一。同样的原因，也导致在网格的大小与结果的质量之间需要取舍平衡。

2）对斜坡为多物质组成时，应分别建立多组件的斜坡模型，以设立不同的碰撞恢复系数。崩塌落石是一个很复杂的过程，斜坡与滚石特性和初始状态的稍微改变都会强烈改变落石的动力特征。因此对未知滚石运动过程最好的评价方法可能是先采用概率的办法进行轨迹预测，然后对大概率事件或高风险事件进行确定性耦合分析。对已知滚石停止点的落石碰撞过程模拟，需要通过工程地质判断调整输入参数，以达到预期的结果[11]。

图3 岩块运动瞬时图片Fig.3 Moving instantaneous picture of rock block

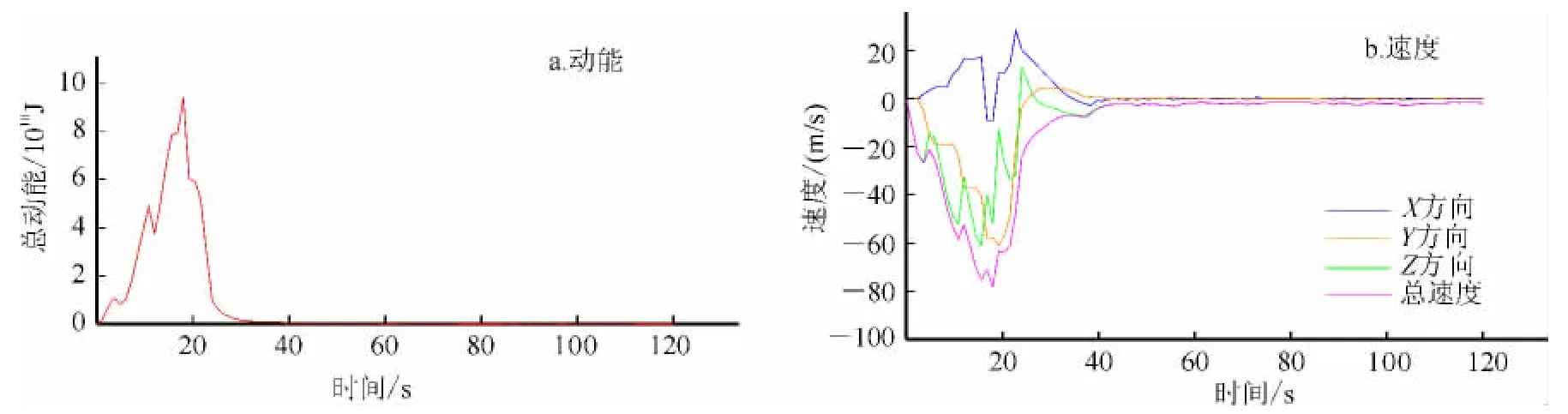
图4 岩块运动过程线Fig.4 Process line of rock block

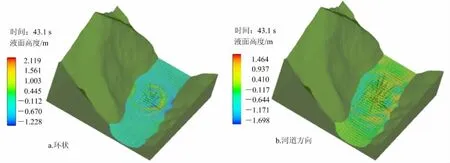
图5 涌浪传播及波速矢量图Fig.5 Impulsive wave propagation and wave velocity vector map

3）由于概率法能更真实准确地预测滚石的运动特性，在硬件容许和算法优化的条件下可考虑将概率方法引入耦合数值模型中。

4）笔者选用了工程中应用最广泛的k-ε湍流模型，其基本思想是用低阶关联量和平均流体性质来模拟未知的高阶关联量。今后可考虑应用LES大涡模型对实际涌浪中大量存在的高Re数湍流激流现象进行有效求解。

5）一般来说，一个从上方滚下的大块石经过弹跳、翻滚、滑动可能分解成许多小块石。碰撞分解的过程在本文中并未涉及。块石弹跳、碰撞、分解然后入水产生涌浪，全过程数值模拟涉及到断裂力学、碰撞固体力学、运动学和流体力学，是目前崩滑体涌浪研究领域研究的最前沿。

4 结论及建议

笔者首次尝试使用耦合GMO碰撞模型的CFD软件预测了崩塌落石产生涌浪的全过程，得到了以下结论和建议。

1）三维流体力学与固体力学耦合分析涌浪可获得从微观到宏观的直观结果，这一方向将是涌浪研究的发展趋势。

2）以剪刀峰河道为原型，建立了一个k-ε湍流模型和GMO碰撞模型的流固耦合模型，网格单元为1827万个，假定的GMO方量为1.2万m3。

3）通过流固耦合计算得到，岩块经过3次弹跳后入水，入水时运动物体的速度达到最大，约为80 m／s，动能也达到最大，约9.3×1011J。入水后，岩块动能持续降低，能量开始传递给水体。在水体作用下，岩块的运动方向与轨迹发生较大变化，下沉时间明显延长。运动物体完全停止后，流体获得的总动能为6.08×1010J，能量传递率约为6.54%。

4）根据航道内涌浪大小分析，在入水区附近（离岸200m内）航道为红色预警区，在离剪刀峰岸线200～350m内航道为橙色预警区，离剪刀峰岸线350m后的航道为黄色预警区。建议将本区段北航道线往南移350m左右，航道内涌浪风险大大降低，航道安全度得到提高。

5）流固耦合分析涌浪是一个新方法、新手段，需要与其他方法进行对比分析，方法自身也尚还有很多方面需要完善，有待深入研究。

（References）：

[1]Valentin Heller.Landslide Generated Impulse Waves：Prediction of Near Field Characteristics[D].Zürich：Eidgenossische Technische Hochschule Zürich，2007.

[2]Bozzolo D，Pamini B.Simulation of Rock-Falls Down a Valley Side[J].Acta Mechanica，1986，63（1）：113-130.

[3]Dourrier F，Dorren L，Nicot F，et al.Toward Objective Rockfall Trajectory Simulation Using a Stochastic Impact Model[J].Geomorphology，2009，110（3／4）：68-79.

[4]Giani G，Giacomini A，Migliazza，et al.Experimental and Theoretical Studies to Improve Rock Fall Analysis and Protection Work Design[J].Rock Mechanics and Rock Engineering，2004，37（5）：369-389.

[5]Chau K T，Wond R H C，Lee C F.Rockfall Problems in Hong Kong and Some New Experimental Results for Coefficient of Restitution[J].Int J Rock Mech Min Sci，1996，35：662-663.

[6]秦志英，陆启韶.基于恢复系数的碰撞过程模型分析[J].动力学与控制学报，2006，4（4）：294-298.Qin Zhiying，Lu Qishao.Analysis of Impact Process Model Based on Restitution Coefficient[J].Journal of Dynamics and Control，2006，4（4）：294-298.

[7]何思明，吴永，李新坡.滚石冲击碰撞恢复系数研究[J].岩土力学，2009，30（3）：623-627.He Siming，Wu Yong，Li Xinpo.Research on Restitution Coefficient of Rock Fall[J].Rock and Soil Mechanics，2009，30（3）：623-627.

[8]沈均，何思明，吴永.滚石对垫层材料的冲击特性研究[J].安徽农业科学，2009，37（17）：8286-8288.Shen Jun，He Siming，Wu Yong.Study on the Impact Properties of Rock-Fall on Cushion Material[J].Journal of Anhui Agricultural Sciences，2009，37（17）：8286-8288.

[9]杨海清，周小平.边坡落石运动轨迹计算新方法[J].岩土力学，2009，30（11）：3411-3416.Yang Haiqing，Zhou Xiaoping.A New Approach to Calculate Trajectory of Rockfall[J].Rock and Soil Mechanics，2009，30（11）：3411-3416.

[10]Mangwandi C，Cheong Y，Adams M，et al.The Coefficient of Restitution of Different Representative Types of Granules [J].Chemical Engineering Science，2007，62（1／2）：437-450.

[11]Rocscience.Rocfall User Manual：Statistical Analysis of Rockfalls[M].[S.l.]：Rocscience Inc，2002：51-59.

[12]Azzoni A，Freitas M.Experimentally Gained Parameters，Decisive for Rock Fall Analysis[J].Rock Mechanics and Rock Engineering，1995，28（2）：111-124.

[13]Day R W.Case Studies of Rockfall in Soft Versus Hard Rock[J].Environmental and Engineering Geoscience，1997，3（1）：133-140.

[14]章广成，向欣，唐辉明.落石碰撞恢复系数的现场试验与数值计算[J].岩石力学与工程学报，2011，30（6）：1266-1273.Zhang Guangcheng，Xiang Xin，Tang Huiming.Field Test and Numerical Calculation of Restitution Coefficient of Rockfall Collision[J].Chinese Journal of Rock Mechanics and Engineering，2011，30（6）：1266-1273.

[15]Jones C L，Higgins J D，Andrew R D.Colorado Rockfall Simulation Program，Version 4.0（for Windows）[R].Colorado：Colorado Department of Transportation，Colorado school of Mines，Colorado Geological Survey，2000.

[16]Guzzetti F，Crosta G，Detti R.STONE：A Computer Program for the Three-Dimensional Simulation of Rock-Falls[J].Computers and Geosciences，2002，28（9）：1079-1093.

[17]Azzoni A，Barbera G，Zaninetti A.Analysis and Prediction of Rockfalls Using a Mathematical Model[J].International Journal of Rock Mechanics and MiningSciences and Geomechanics Abstracts，1996，33（4）：178.

[18]Choi B H，Pelinovsky E，Kim D C，et al.Two-and Three-Dimensional Computation of Solitary Wave Runup on Non-Plane Beach[J].Nonlin Processes Geophys，2008，15：489-502.

[19]Silvia B，Marco P.Shallow Water Numerical Model of the Wave Generated by the Vajont Landslide[J].Environmental Modelling ＆ Software，2011（26）：406-418.

[20]Montagna F，Bellotti G，Risio M D.3DNumerical Modeling of Landslide-Generated Tsunamis Around a Conical Island[J].Nat Hazards，2011（58）：591-608.

[21]Pastor M，Herreros I，Fernández M J A，et al.Modelling of Fast Catastrophic Landslides and Impulse Waves Induced by Them in Fjords，Lakes and Reservoirs[J].Engineering Geology，2009，109：124-134.

[22]Stéphane Abadie，Denis Morichon，Stéphan Grilli，et al.Numerical Simulation of Waves Generated by Landslides Using a Multiple-Fluid Navier-Stokes Model[J].Coastal Engineering，2010（57）：779-794.

[23]Huang B L，Chen L D，Peng X M，et，al.Assessment of the Risk of Rockfalls in Wu Gorge，Three Gorges，China[J].Landslides，2010，7（1）：1-11.

[24]Flow Science Inc.Flow-3DUser Manual[M].New Mexico：Flow Science Inc，2012.