全尺寸射孔完井水平井筒流动压降实验

魏建光，王小秋，陈海波，张权

（1. 东北石油大学石油工程学院；2. 中国石油大学（北京）石油工程学院；3. 大庆油田第三采油厂工程技术大队）

0 引言

射孔完井水平井筒变质量流与普通管流相比十分复杂，其复杂性主要体现在 2个方面：①射孔孔眼的存在使井筒管壁粗糙度增加，从而增大了井筒壁面摩擦压降；②壁面入流与主流混合后改变了井筒管壁附近边界层和主流速度剖面，进而改变了井筒压降。水平井筒复杂流动压降规律是水平井生产动态预测、井眼轨迹设计、完井参数优化设计、壁面入流控制方法选择的重要依据[1-4]。因此，国内外很多学者对射孔完井水平井筒单相流动压降规律进行了比较深入的实验研究[5-18]，但这些研究存在3点不足：①都是采用根据相似原理设计的小尺寸实验井段来模拟水平井筒，不能够同时实现几何相似、运动相似和动力相似，与水平井筒实际生产情况存在一定偏差；②大多数学者采用有机玻璃管模拟水平井筒且实验流体为清水，不能反映水平井筒实际生产情况；③没有系统详细地给出射孔相位、射孔孔径、射孔密度等参数对各种压降的影响规律。本文设计射孔完井水平井筒复杂流动实验系统，采用外径139.7 mm的壁面打孔套管模拟射孔完井水平井筒，通过模拟实验研究射孔参数（射孔相位、射孔孔径、射孔密度）对壁面摩擦压降、混合压降、总压降的影响规律，以及壁面注入比对总压降梯度、混合压降梯度、壁面摩擦压降梯度和加速度压降梯度的影响规律，为射孔完井水平井筒压降模型的建立提供科学依据。

1 实验

设计了射孔完井水平井筒复杂流动实验系统（见图1）。实验系统由3部分组成：模拟实验单元、实验流体供给与控制系统、数据采集分析系统。

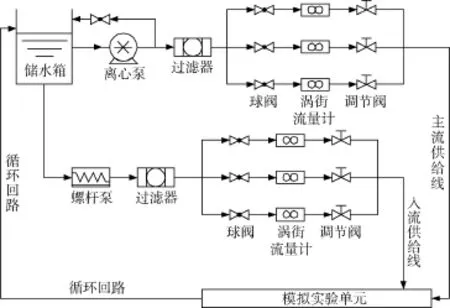
图1 射孔完井水平井筒复杂流动实验系统

模拟实验单元（见图2）中的实验井段为内径124.0 mm（外径139.7 mm）的套管，外套内径149.1 mm（外径 190.5 mm）的套管，环空缠有致密纱布。模拟实验单元长 6.5 m，两测压点间距离为 6.0 m。为提高测量精度，两测压点间压差利用柔软透明橡胶管测得，测量精度为 1 Pa。为了使壁面入流均匀，模拟实验单元两端各有 1个进液口（1个在上侧，1个在下侧）。

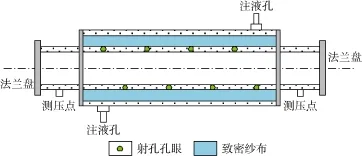
图2 模拟实验单元示意图

实验用黏度10 mPa·s左右的白油代替常规原油。每天开展实验之前均先测量室内温度和白油黏度，当室内温度和白油黏度与前一天基本一致时才开展实验。

设计了3种实验井段射孔相位：45°螺旋射孔（见图 3）、90°螺旋射孔（见图 4）、180°螺旋射孔（见图 5）。设计了3种射孔密度：8孔/m、16孔/m、24孔/m。设计了3种射孔孔径：10 mm、20 mm、30 mm。主流雷诺数设计为1 000～20 000，对应的流量为90～1 850 m3/d。壁面注入比（单位长度井筒壁面入流流量与主流流量的比值）设计为0.01%～10.00%。

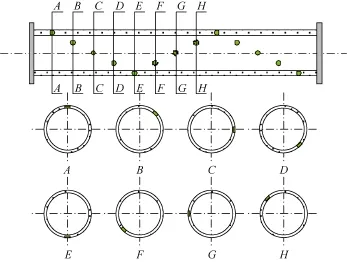
图3 45°相位螺旋射孔示意图

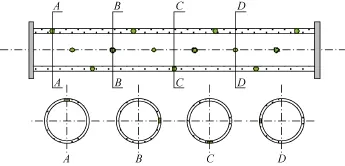
图4 90°相位螺旋射孔示意图

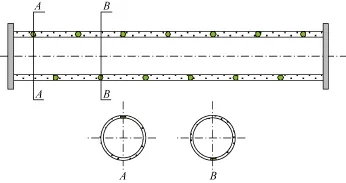
图5 180°相位螺旋射孔示意图

利用设计的实验系统，可以测得射孔套管液流的壁面摩擦压降和总压降。无壁面入流条件下模拟实验单元中两测压点间的压差，即为壁面摩擦压降；有壁面入流条件下模拟实验单元中两测压点间的压差，即为总压降。测得壁面摩擦压降和总压降后，根据动量守恒定律可计算出加速度压降，再用总压降减去壁面摩擦压降和加速度压降就可计算出混合压降。

2 实验结果

2.1 射孔参数对壁面摩擦压降的影响规律

图 6—图 8分别为无壁面入流时，不同射孔密度（射孔孔径为20 mm，射孔相位为90°）、不同射孔孔径（射孔密度为16孔/m，射孔相位为90°）、不同射孔相位（射孔密度为16孔/m，射孔孔径为20 mm）条件下射孔套管液流壁面摩擦压降梯度与主流雷诺数的关系曲线。

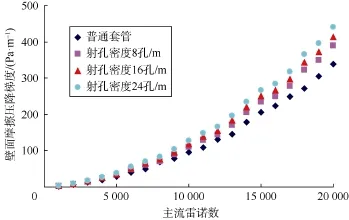
图6 不同射孔密度时壁面摩擦压降梯度与主流雷诺数关系

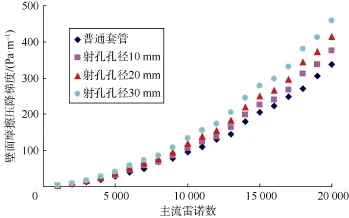
图7 不同射孔孔径时壁面摩擦压降梯度与主流雷诺数关系

由图6—图8可知，射孔密度、射孔孔径、射孔相位均对射孔套管液流的壁面摩擦压降有显著影响，随着射孔密度、射孔孔径、射孔相位的增大，射孔套管液流的壁面摩擦压降均增大。此外，无壁面入流时射孔套管液流的壁面摩擦压降比普通套管（没有射孔的套管）液流的壁面摩擦压降大，说明射孔孔眼的存在使套管的壁面粗糙度增大，进而导致壁面摩擦压降增大。

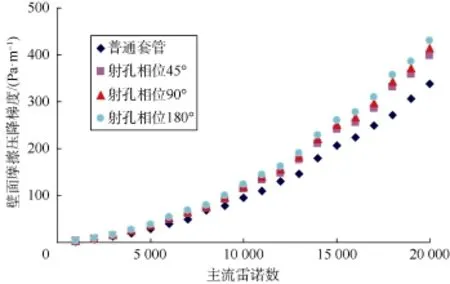
图8 不同射孔相位时壁面摩擦压降梯度与主流雷诺数关系

2.2 射孔参数对总压降的影响规律

图 9—图 11分别为射孔套管出口主流雷诺数为5 000时，不同射孔密度（射孔孔径为20 mm，射孔相位为90°）、不同射孔孔径（射孔密度为16孔/m，射孔相位为90°）、不同射孔相位（射孔密度为16孔/m，射孔孔径为20 mm）条件下射孔套管液流总压降梯度与壁面注入比的关系曲线。

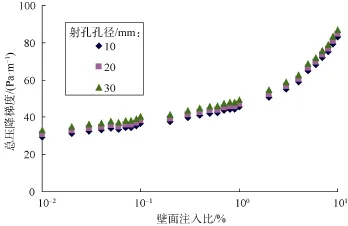
图10 不同射孔孔径时总压降梯度与壁面注入比关系

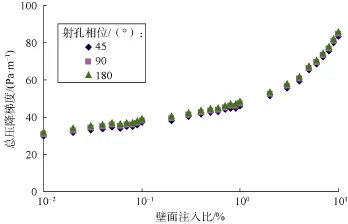
图11 不同射孔相位时总压降梯度与壁面注入比关系

由图9—图11可知，随着射孔密度、射孔孔径、射孔相位的增大，射孔套管液流的总压降均增大。此外，射孔套管出口主流雷诺数相同时，随着壁面注入比的增大，射孔套管液流的总压降增大。

2.3 射孔参数对混合压降的影响规律

图12—图14为射孔套管出口主流雷诺数为5 000时，不同射孔密度（射孔孔径为20 mm，射孔相位为90°）、不同射孔孔径（射孔密度为16孔/m，射孔相位为90°）、不同射孔相位（射孔密度为16孔/m，射孔孔径为20 mm）条件下射孔套管液流混合压降梯度与壁面注入比的关系曲线。

图12 不同射孔密度时混合压降梯度与壁面注入比关系

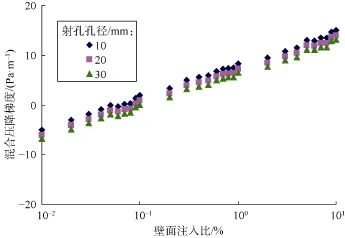
图13 不同射孔孔径时混合压降梯度与壁面注入比关系

图14 不同射孔相位时混合压降梯度与壁面注入比关系

由图12—图14可知，随着射孔密度、射孔孔径、射孔相位的增大，射孔套管液流的混合压降均减小。此外，射孔套管出口主流雷诺数相同时，随着壁面注入比的增大，射孔套管液流的混合压降增大，但壁面注入比对射孔套管液流混合压降的影响存在一个临界值（本研究条件下为 0.05%～0.10%）。当壁面注入比小于临界值时，射孔套管液流混合压降小于零，说明此时壁面入流的存在使射孔套管液流总压降减小；当壁面注入比大于临界值时，射孔套管液流混合压降大于零，说明此时壁面入流的存在使射孔套管液流总压降增大。壁面注入比临界值的大小主要受射孔密度和射孔孔径的影响，随着射孔密度和射孔孔径增大，临界壁面注入比增大。

2.4 壁面注入比对各种压降的影响规律

图 15、图 16分别为射孔套管出口主流雷诺数为5 000、15 000时射孔套管液流的总压降梯度、壁面摩擦压降梯度、混合压降梯度、加速度压降梯度与壁面注入比的关系曲线。可知，在两种主流雷诺数条件下，壁面注入比小于0.10%时，射孔套管液流的加速度压降都可以忽略；壁面注入比大于0.10%时，随着壁面注入比增大，射孔套管液流的加速度压降显著增加。此外，加速度压降受射孔套管出口主流雷诺数影响，主流雷诺数为5 000、壁面注入比为10.00%时的加速度压降与壁面摩擦压降接近；而主流雷诺数为15 000、壁面注入比为 10.00%时的加速度压降大于壁面摩擦压降。

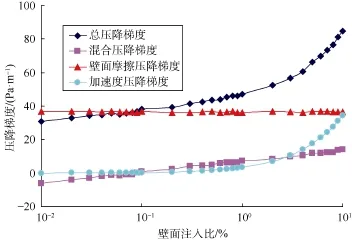
图15 主流雷诺数为5 000时各压降梯度与壁面注入比关系

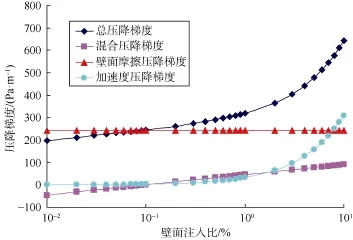
图16 主流雷诺数为15 000时各压降梯度与壁面注入比关系

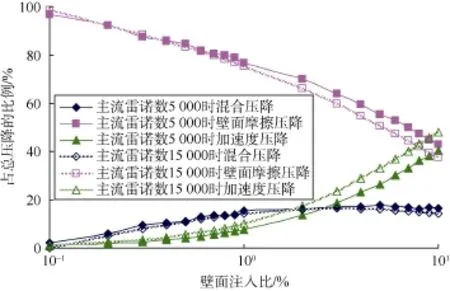
图17 各压降占总压降的比例与壁面注入比关系

图17 为射孔套管出口主流雷诺数分别为5 000和1 5000时射孔套管液流的混合压降、壁面摩擦压降、加速度压降占总压降的比例与壁面注入比的关系曲线。可知：①随着壁面注入比的增大，射孔套管液流的壁面摩擦压降占总压降的比例逐渐减小，加速度压降占总压降的比例逐渐增大。②壁面注入比小于1.00%时，混合压降占总压降的比例随壁面注入比的增大而增大；壁面注入比大于1.00%时，混合压降占总压降的比例基本保持不变（15%左右）。③壁面注入比小于0.10%时，两种主流雷诺数条件下，射孔套管液流的壁面摩擦压降占总压降的比例都在 97%左右，混合压降和加速度压降可以忽略。④壁面注入比小于1.00%时，壁面摩擦压降、混合压降、加速度压降占总压降的比例基本不受主流雷诺数影响。

3 结论

设计了射孔完井水平井筒复杂流动实验系统，采用外径139.7 mm的壁面打孔套管模拟射孔完井水平井筒，并用黏度 10 mPa·s左右的白油作为实验流体，能够比较真实地反映水平井筒实际生产情况。

研究了射孔参数对壁面摩擦压降、混合压降、总压降的影响规律。实验结果表明：随着射孔密度、射孔孔径、射孔相位的增大，射孔套管液流的壁面摩擦压降和总压降均增大，混合压降减小。

研究了壁面注入比对各种压降的影响规律。实验结果表明：①射孔套管出口主流雷诺数相同时，随着壁面注入比的增大，射孔套管液流的总压降和混合压降均增大。当壁面注入比小于临界值（本研究条件下为0.05%～0.10%）时，混合压降小于零，此时壁面入流的存在使总压降减小；当壁面注入比大于临界值时，混合压降大于零，此时壁面入流的存在使总压降增大。壁面注入比小于0.10%时，射孔套管液流的加速度压降可以忽略；壁面注入比大于0.10%时，随着壁面注入比增大，加速度压降显著增加。②随着壁面注入比的增大，射孔套管液流的壁面摩擦压降占总压降的比例逐渐减小，加速度压降占总压降的比例逐渐增大。壁面注入比小于1.00%时，混合压降占总压降的比例随壁面注入比的增大而增大；壁面注入比大于1.00%时，混合压降占总压降的比例基本保持不变。壁面注入比小于0.10%时，壁面摩擦压降占总压降的比例都在 97%左右，混合压降和加速度压降可以忽略。壁面注入比小于1.00%时，壁面摩擦压降、混合压降、加速度压降占总压降的比例基本不受主流雷诺数影响。

[1] 曾晓晶, 同登科. 水平井水平段最优长度设计方法改进[J]. 石油勘探与开发, 2011, 38(2)： 216-220.Zeng Xiaojing, Tong Dengke. An improvement of the design method of optimal horizontal wellbore length[J]. Petroleum Exploration and Development, 2011, 38(2)： 216-220.

[2] Asheim H, Kolnes J, Oudeman P. A flow resistance correlation for completed wellbore[J]. Journal of Petroleum Science and Engineering, 1992, 8(2)： 97-104.

[3] 周生田, 张琪, 李明忠, 等. 水平井筒变质量流体流动实验研究[J]. 石油大学学报： 自然科学版, 1998, 22(5)： 53-55.Zhou Shengtian, Zhang Qi, Li Mingzhong, et al. Experimental study on variable mass fluid flow in horizontal wells[J]. Journal of the University of Petroleum, China： Natural Science Edition, 1998, 22(5)：53-55.

[4] 张世明, 周英杰, 宋勇, 等. 鱼骨状分支水平井井形设计优化[J].石油勘探与开发, 2011, 38(5)： 606-612.Zhang Shiming, Zhou Yingjie, Song Yong, et al. Design optimization for the horizontal well pattern with herringbone-like laterals[J].Petroleum Exploration and Development, 2011, 38(5)： 606-612.

[5] Su Z, Gudmundsson J S. Friction factor of perforation roughness in pipes[R]. SPE 26521, 1993.

[6] Su Z, Gudmundsson J S. Pressure drop in perforated pipes：Experiments and analysis[R]. SPE 28800, 1994.

[7] Ihara M, Brill J P, Shoham O. Experimental and theoretical investigation of two-phase flow in horizontal wells[R]. SPE 24766, 1992.

[8] Ihara M, Shimizu N. Effect of accelerational pressure drop in a horizontal wellbore[R]. SPE 26519, 1993.

[9] Ihara M, Yanai K, Takao S. Two-phase flow in horizontal wells[J].SPE Production & Facilities, 1995, 10(4)： 249-256.

[10] Yuan H, Sarica C, Brill J P. Effect of perforation density on single phase liquid flow behavior in horizontal wells[R]. SPE 37109, 1996.

[11] Yuan H. Investigation of single phase liquid flow behavior in horizontal wells[D]. Tulsa： The University of Tulsa, 1997.

[12] Yuan H, Sarica C, Brill J P. Effect of completion geometry and phasing on single-phase liquid flow behavior in horizontal wells[R].SPE 48937, 1998.

[13] Ouyang L B. Single phase and multiphase fluid flow in horizontal wells[D]. Stanford： Stanford University, 1998.

[14] Ouyang L B, Petalas N, Arbabi S, et al. An experimental study of single-phase and two-phase fluid flow in horizontal wells[R]. SPE 46221, 1998.

[15] 庞伟, 陈德春, 张仲平, 等. 非均质油藏水平井分段变密度射孔优化模型[J]. 石油勘探与开发, 2012, 39(2)： 214-221.Pang Wei, Chen Dechun, Zhang Zhongping, et al. Segmentally variable density perforation optimization model for horizontal wells in heterogeneous reservoirs[J]. Petroleum Exploration and Development,2012, 39(2)： 214-221.

[16] 周生田, 张琪, 李明忠, 等. 水平井变质量流研究进展[J]. 力学进展, 2002, 32(1)： 119-127.Zhou Shengtian, Zhang Qi, Li Mingzhong, et al. The advances on the variable mass flow in horizontal wells[J]. Advances in Mechanics,2002, 32(1)： 119-127.

[17] 汪志明, 张松杰, 薛亮, 等. 水平井筒射孔完井变质量流动压降规律[J]. 石油钻采工艺, 2007, 29(3)： 4-7.Wang Zhiming, Zhang Songjie, Xue Liang, et al. Pressure drop of variable mass flow in perforation completion of horizontal wellbore[J]. Oil Drilling & Production Technology, 2007, 29(3)： 4-7.

[18] 汪志明, 肖京男, 王小秋, 等. 水平井变质量流动压降规律实验研究[J]. 实验流体力学, 2011, 25(5)： 26-29.Wang Zhiming, Xiao Jingnan, Wang Xiaoqiu, et al. Experimental study for pressure drop of variable mass flow in horizontal well[J].Journal of Experiments in Fluid Mechanics, 2011, 25(5)： 26-29.