基于元建模的裂缝性气藏累计产量预测

Seifi A，Kazemzadeh M B，Mohammadi H

（伊朗Amirkabir科技大学工业工程系）

0 引言

一般采用数值模拟方法预测油气藏的累计产量。数值模拟属于密集型计算过程，计算量大，采用元建模方法并建立合适的元模型，可以减小计算量、提高计算效率。元模型是一种代理数学方程，主要用于近似表示复杂体系内的输入-输出关系[1]。元建模基本步骤[1-6]包括：①定义输入变量及相应的输出响应；②进行实验设计（DoE），选择样本点，并确定各样本点的响应；③构建元模型，建立输入变量与输出响应之间的关系；④通过试验点验证元模型的准确性。

本文以伊朗南部某大型裂缝性气藏为例，基于元建模方法对该气藏在18年规划周期内的累计产量进行预测。建立3种不同的元模型（传统二次模型、乘性模型及径向基函数（RBF）模型），并利用基于数值模拟的气藏累计产量预测结果对3种模型进行验证和对比。

1 气藏基本参数估计及数值模拟

为了对元模型的准确性进行验证和对比，在建立元模型之前预先估算了气藏的基本参数（孔隙度、渗透率及含水饱和度）并对气藏进行了数值模拟。

本文研究对象为伊朗南部某大型裂缝性气藏。对该气藏进行网格划分，x、y、z方向的网格数分别为45、37和95，总网格数为158 175。对探井的FMI测井数据进行了解释和分析，计算了裂缝参数（方位角、倾角及密度），考虑裂缝参数的影响，采用序贯指示模拟（SIS）法和序贯高斯模拟（SGS）法[7]对各网格的孔隙度和渗透率进行了估算。

为了更真实地反应本文研究气藏的孔隙空间分布特征，首先用裂缝面模型对孔隙度模型进行了改进，即根据裂缝面模型求取孔隙度分布的变差函数，然后选用相关的变差函数估算各网格的孔隙度。采用序贯高斯模拟（SGS）法，共获得了孔隙度分布的30个模拟结果，并选择了拟合效果最佳的模拟结果。

获取了研究区13口井的岩心渗透率数据。基于2个水平方向（x，y方向）和1个垂直方向（z方向）的裂缝参数计算了渗透率修正系数，并生成了 x，y和z方向的变差函数。采用序贯指示模拟（SIS）法，对裂缝参数分布进行了模拟，进而得到考虑裂缝影响的渗透率模型。

对渗透率和孔隙度模型进行了三维可视化处理（见图 1），以直观显示储集层的连通性、阻流带发育情况及高孔高渗带的分布。

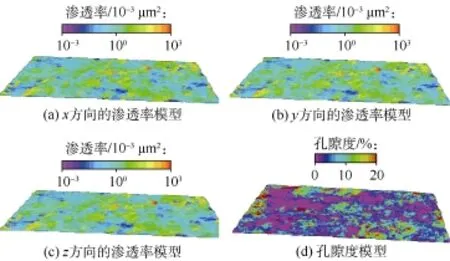
图1 x，y和z方向的渗透率模型及孔隙度模型

基于已估算的气藏基本参数，建立了该气藏的Eclipse数值模型，以对元模型进行验证和对比。采用Eclipse软件在5台并行PC机（CPU为双核Intel 3.4 GHz）上计算了1口井生产18年的累计产量，耗时超过15 h。如果对所有158 175个网格进行计算，将会耗费很长时间，而采用元建模的方法可以提高计算效率。

2 元建模

2.1 输入变量和输出响应

本文假定与气藏累计产量相关的参数为 x方向的渗透率（Kx）、y方向的渗透率（Ky）、z方向的渗透率（Kz）、孔隙度（φ）和含水饱和度（Sw），则气藏内某井18年内的累计产量可表示为：

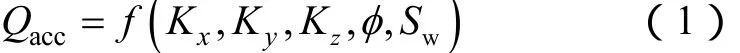
（3）式中，Y为输出响应，X为输入变量，F(X)为近似响应函数，ε为误差。本文建立了3种不同的元

因此，元建模的输入变量为Kx，Ky，Kz，φ和Sw，输出响应为Qacc。

2.2 实验设计

实验设计方法可分为两类：依赖于模型的设计和独立于模型的设计，一般情况下独立于模型的设计在确定性计算机实验中的应用效果更佳[8]。在独立于模型的实验设计中，最常用的最优性判断准则包括最大熵、均方误差、极大极小和极小极大 4种。本文采用最大熵设计方法[9-10]，最大熵设计是一种序贯方法，通过搜索参数空间寻找设计点，进而使相应设计点的实验提取信息（熵）最大化，可采用遗传算法[11]求解。

进行气藏元建模实验设计时，应考虑储集层特征[11]。由于元建模的目的是寻找累计产量最高的点，在对元模型进行验证时只考虑高潜力点，不考虑元模型在低潜力点的拟合效果。本文研究的气藏复杂且网格数量大，因此选用HIP经验函数（储量计算公式）排除研究空间内的低潜力点。HIP经验函数的表达式为：

利用HIP经验函数可以生成气藏网格空间的产能等值线（见图 2），以显示不同位置的产气潜力。初始设计点的位置选在等值线的峰值处。基于等值线图中的信息，选定了 200个高潜力点作为输入点。考虑到元模型内参数的数量及相互关系，为了满足估算模型参数所需的自由度，至少应开展25次实验，基于最大熵准则从200个高潜力点中选取25个点作为设计点[11]。

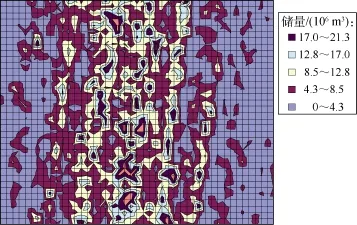
图2 由HIP经验函数生成的储量等值线图

2.3 元模型建立

元建模最关键的步骤是建立输入变量与输出响应之间的关系，即建立元模型。元模型的一般形式为：模型，包括传统二次模型、乘性模型和径向基函数（RBF）模型，并对3种模型进行验证和对比。

2.3.1 传统二次模型

传统二次模型的优点为：可以分别确认各因素的影响程度，有助于从模型中剔除影响较小的因素，继而生成更平滑的模型。用于计算气藏累计产量的二次模型可表示为：

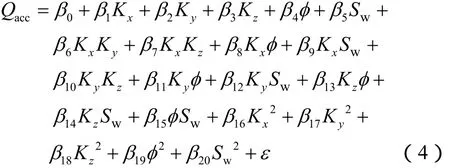
上述二次模型中共包含21个系数（β0～β20），部分系数不具有明显的统计意义，因而可以将相应的项从模型中去除，从而简化模型。为了确定各系数的重要性，定义原假设为 βi=0（i=0，1，…，20），备择假设为βi≠0，采用t检验法进行假设检验，显著性水平α取为 0.1。检验结果表明：仅有 7个系数（β0，β1，β3，β4，β5，β6，β7）对输出响应有显著影响。因此，二次模型可简化为：

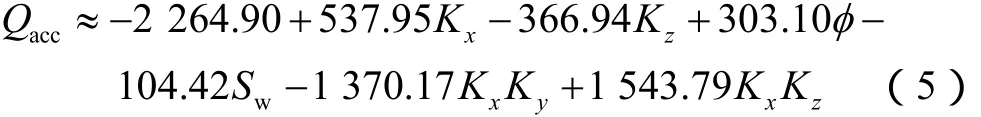
2.3.2 乘性模型

以乘性模型为基础，可构建一种近似表示输入变量与输出响应间关系的替代模型，该近似模型强调气藏静态参数间相互作用对气藏产量的影响。乘性模型中各因素的影响具有倍增性，例如，在任何给定点，如果含水饱和度高，即使渗透率和孔隙度很高，气藏产量仍然很低。因此，为了确保每口井均有较高的产量，泄气半径内的所有气藏参数均需有利于增产。构建乘性模型的思路与HIP经验函数一致。用于计算气藏累计产量的乘性模型可表示为：

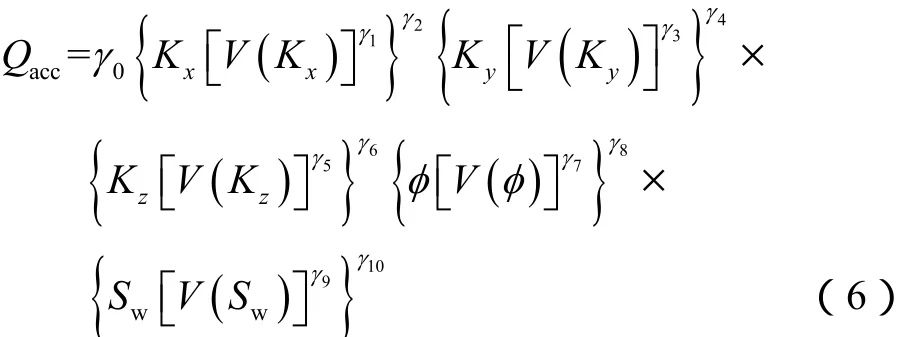
上述乘性模型中包含各气藏参数的方差（用 V(·)表示），以表征气藏物性垂向变化以及因对各参数属性模型进行网格粗化所导致的不确定性。模型中包含 11个系数（γ0～γ10），基于25个设计点的气藏数值模拟数据，采用非线性回归分析法，对各系数进行了估算。拟合后的乘性模型为：

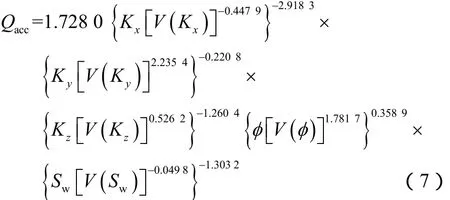
2.3.3 RBF模型

以径向基函数（RBF）模型表示输入变量与输出响应间的关系必须具备 2个主要条件：目标函数为噪声函数，且噪声因子的影响随着径向点与参考点间距离的增加而严格递减或递增。RBF模型中包含1个连接界面，以衔接输入变量与目标函数。用于计算气藏累计产量的RBF模型可表示为：

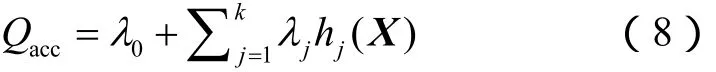
其中

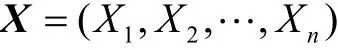
（8）式中，hj(X)为径向基函数，表示径向点（Aj）处属性向量Xj的非线性界面函数估计值。确定模型形式的关键在于选定合适的径向基函数，常用的标准径向基函数包括高斯RBF、薄板样条RBF、多二次RBF、逆多二次RBF等[12]。这些径向基函数各有优点，但高斯RBF的使用频率更高[12-15]。对本文的研究对象而言，随着与参考点（Ar）间距离的增大，径向点对目标函数的影响减弱，因此，高斯RBF是较好的选择，其表达式为：

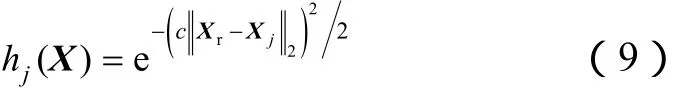
（9）式中，c是一个标量，可以通过获取更为精确的近似值的方式进行优化，且通常与模型中的一些方差相关。‖Xr-Xj‖2为Xr-Xj的欧氏范数，Xr为参考点处属性微量，Xr与Xj均为包含475个元素的长向量（5个气藏参数、95个层位）。

在建立本文所研究气藏的RBF模型时，某个设计点被视为参考点 Ar，邻近网格的位置可以被视为参考点周围的径向点Aj，图 3显示了给定的参考点周围的径向点分布情况。用于估算 RBF模型中各系数（λ0，λ1，…，λk）的数据集由 25个设计点及每个设计点周围的24个径向点的气藏参数组成，基于这些数据，采用线性回归分析方法即可估算模型中各系数。

2.4 元模型验证

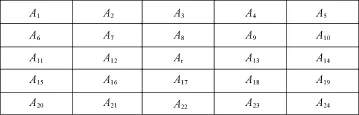
图3 参考点周围的径向点分布情况

表1为数值模拟得到的25个设计点累计产量（用Eclipse软件计算）以及采用3种元模型建模后求得的累计产量，表中的误差为各模型的输出响应（即累计产量）相对数值模拟计算结果的误差。为了检验各元模型的有效性，选择 7个试验点（在最小泄气半径范围内），分别采用数值模拟方法和3种元模型计算累计产量（见表2）。

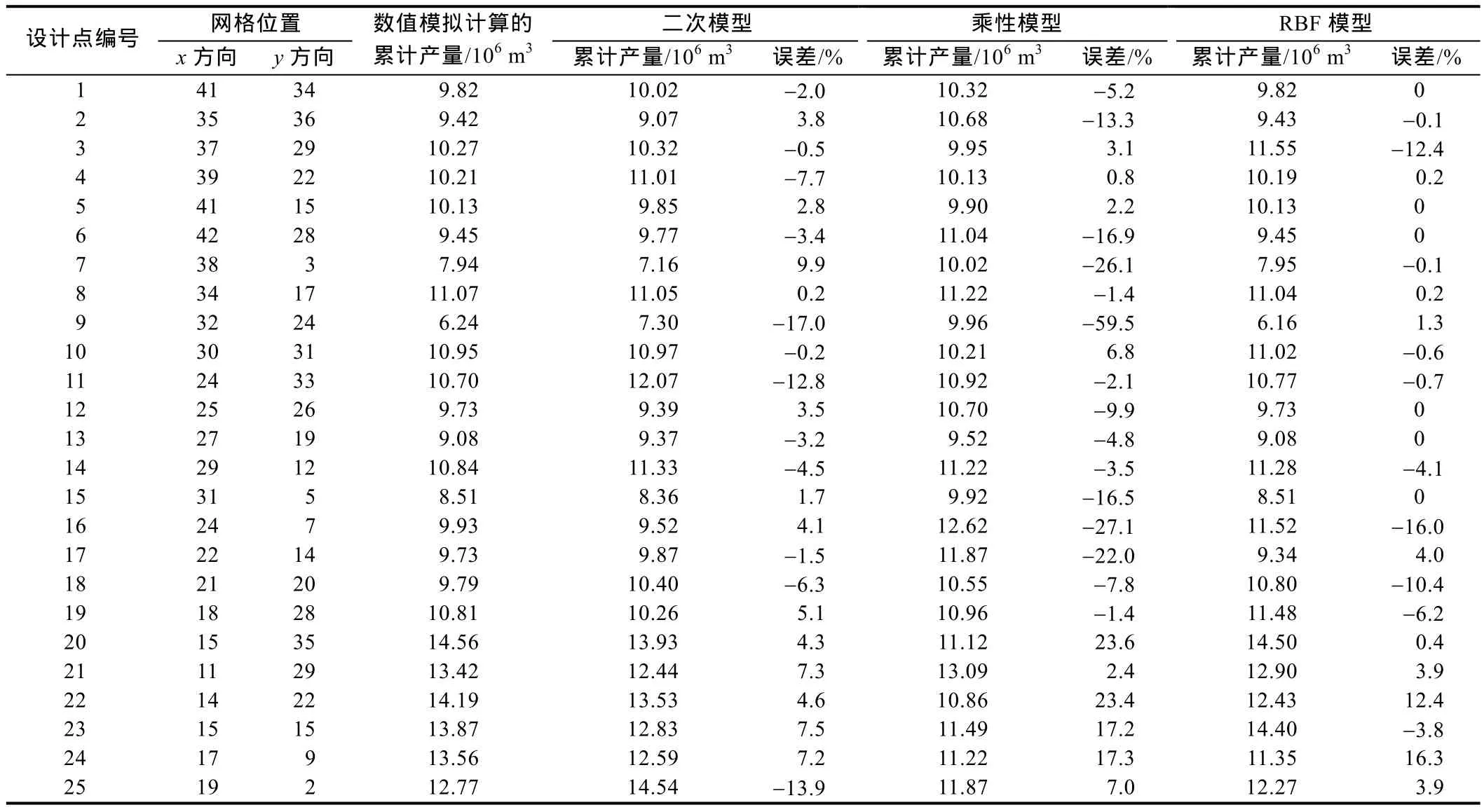
表1 设计点数值模拟和元建模计算的累计产量

表2 试验点数值模拟和元建模计算的累计产量

由表1可知：①在25个设计点，基于二次模型、乘性模型、RBF模型预测的累计产量均与数值模拟预测结果有较好的一致性，回归分析的复相关系数值分别为94.6%、96.6%和96.6%；②以25个设计点数值模拟预测累计产量为参照，RBF模型的预测准确性优于另外2种模型。

由表2可知：①在26号点，二次模型、乘性模型和 RBF模型的累计产量预测准确性都较差，说明 26号点为低潜力点，这与实际情况一致；②在 7个试验点，二次模型、乘性模型、RBF模型的平均误差分别为15.5%、14.1%和6.6%；③若剔除26号点，二次模型、乘性模型、RBF模型的平均误差分别降为7.6%、8.2%和1.6%。

综上所述，二次模型、乘性模型和RBF模型均有较好的累计产量预测准确性，RBF模型的累计产量预测准确性优于另外两种模型。主要原因可能是RBF模型的输入变量更多，因此，如果能获取各网格的气藏参数数据，RBF模型是累计产量预测的最佳选择。

2.5 元模型应用

利用上述 3种元模型，可在几秒钟内计算出整个气藏空间中任何位置的累计产量，如果采用数值模拟方法，则需耗时数月。图 4为基于二次模型求得的气藏累计产量等值线图，累计产量在12.8×106m3以上的区域为高潜力区，可作为建设生产井的备选区。

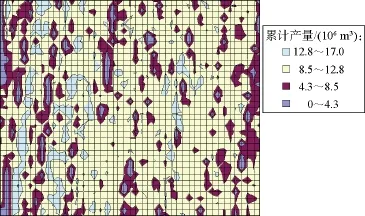
图4 基于二次模型求得的气藏累计产量等值线图

3 结论

在建立元模型之前预先估算了气藏的基本参数（孔隙度、渗透率及含水饱和度）并对气藏进行了数值模拟。

将气藏内某点18年规划周期内的累计产量表示为x方向的渗透率、y方向的渗透率、z方向的渗透率、孔隙度和含水饱和度的函数。采用HIP经验函数排除了研究空间内的低潜力点，并基于最大熵准则选取了25个高潜力点作为设计点。

建立了3种元模型（二次模型、乘性模型和RBF模型），基于各模型预测了25个设计点和7个试验点处的累计产量，并结合数值模拟预测结果进行了验证和对比。结果表明：与数值模拟方法相比，元建模方法的计算时间大幅缩短；各模型均有较好的累计产量预测准确性；RBF模型的累计产量预测准确性优于另外2种模型。

符号注释：

Kx——x方向的渗透率，10-3μm2；Ky——y 方向的渗透率，10-3μm2；Kz——z方向的渗透率，10-3μm2；φ——孔隙度，%；Sw——含水饱和度；Qacc——气藏某井18年内的累计产量，106m3；Vb——网格体积，m3；Y——输出响应；X——输入变量；F(X) ——近似响应函数；ε——误差；β0—β20——二次模型中的系数；V(·)——方差；γ0—γ10——乘性模型中的系数；λ0—λk——RBF模型中的系数；hj(X)——径向基函数；n——变量个数；k——参考点周围径向点个数；c——RBF模型中的标量；Xr——参考点 Ar处的属性向量；Xj——径向点 Aj处的属性向量。

[1] Güyagüler B. Optimization of well placement and assessment of uncertainty[D]. Stanford： Stanford University, 2002.

[2] 庞伟, 陈德春, 张仲平, 等. 非均质油藏水平井分段变密度射孔优化模型[J]. 石油勘探与开发, 2012, 39(2)： 214-221.Pang Wei, Chen Dechun, Zhang Zhongping, et al. Segmentally variable density perforation optimization model for horizontal wells in heterogeneous reservoirs[J]. Petroleum Exploration and Development,2012, 39(2)： 214-221.

[3] Yeten B, Durlofsky L J, Aziz K. Optimization of nonconventional well type, location and trajectory[R]. SPE 77565, 2002.

[4] Foroud T, Seifi A, Hassani H. Surrogate-based optimization of horizontal well placement in a mature oil reservoir[J]. Petroleum Science and Technology, 2012, 30(11)： 1091-1101.

[5] Mohammadi H, Seifi A, Foroud T. A robust Kriging model for predicting accumulative outflow from a mature reservoir considering a new horizontal well[J]. Journal of Petroleum Science and Engineering, 2012, 82/83： 113-119.

[6] 何东博, 王丽娟, 冀光, 等. 苏里格致密砂岩气田开发井距优化[J]. 石油勘探与开发, 2012, 39(4)： 458-464.He Dongbo, Wang Lijuan, Ji Guang, et al. Well spacing optimization for Sulige tight sand gas field, NW China[J]. Petroleum Exploration and Development, 2012, 39(4)： 458-464.

[7] Etminan A H, Seifi A. An improved model for geostatistical simulation of fracture parameters and their effect on static and dynamic models[J]. The Open Petroleum Engineering Journal, 2008, 1： 47-57.

[8] Mckay M D, Beckman R J, Conover W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 2000, 42(1)： 55-61.

[9] Sacks J, Welch W, Mitchell T, et al. Design and analysis of computer experiments (with discussion)[J]. Statist Sci, 1989, 4(4)： 409-423.

[10] Ko C W, Lee J, Queyranne M. An exact algorithm for maximum entropy sampling[J]. Operations Research, 1995, 43(4)： 684-691.

[11] Seifi A, Karimifar M J. Entropy based spatial design： A genetic algorithm approach (case study)[J]. World Academy of Science,Engineering and Technology, 2008, 45： 637-646.

[12] Chen V C P, Tsui K L, Barton R R, et al. A review on design,modeling and applications of computer experiments[J]. IIE Transactions,2006, 38(4)： 273-291.

[13] Ball K, Sivakumar N, Ward J D. On the sensitivity of radial basis interpolation to minimal data separation distance[J]. Constructive Approximation, 1992, 8(4)： 401-426.

[14] Venkataraman R. Application of the method of experimental design to quantify uncertainty in production profiles[R]. SPE 59422, 2000.

[15] Jakobsson S, Patriksson M, Rudholm J, et al. A method for simulation based optimization using radial basis functions[J].Optimization and Engineering, 2010, 11(4)： 501-532.