基于主成分分析的人工智能台风路径预报模型

黄小燕 金龙

1南京信息工程大学大气科学学院，南京210044

2广西壮族自治区气象减灾研究所，南宁530022

3广西壮族自治区气候中心，南宁530022

1 引言

台风是影响我国的重要灾害性天气系统之一，往往会造成严重的经济损失和人员伤亡。所以对台风路径的预报，历来受到人们的关注。对此国内外进行了许多的研究，建立了各种预报方法，其中最主要的是数值模式的动力预报和客观统计预报，主观经验预报等三种方法（魏鼎文和张捷迁，1978；倪允琪等，1981；金一鸣，1983）。目前气象业务上的台风移动路径短期预报一般运用统计模式建立预报方程，常用的数学建模方法主要是多元分析和时间序列分析方法等（周家斌和黄嘉佑，1997；丁裕国等，2002），其主要特点是对某个气象预报对象，建立一个统计预报方程对预报对象的未来状况做出预报计算。

台风路径的变化受到台风环境场和台风系统内部的热力、动力等多种因素的综合影响，十分复杂，因此传统的线性预报方法对于提高台风路径的预报并不是太明显。近年来，随着人工智能技术的发展，人工神经网络方法在很多学科领域取得了一些很好的研究成果（严军和刘健文，2005；陈刚毅等，2005；金龙等，2000；刘妹琴等，2005；哈斯巴干等，2004；李爱军等，2003），而遗传算法是近年来人工智能技术领域十分广泛采用的一种基于自然选择和自然遗传的全局优化算法（洪梅等，2007；胡娅敏等，2006；Zheng et al.，2003；郭章林等，2004）。遗传算法的重要特点是，通过模仿生物进化过程，采用选择、交叉和变异三种遗传进化操作，在遗传种群的个体间进行信息交换，不断产生新的优良种群，是一种不依赖于梯度信息的群体搜索计算方法，对于复杂和非线性问题的求解十分有效（Haupt et al.，2006；张韧等，2008）。另一方面，由于实际的气象预报建模研究，其预报模型的预报效果，除了与线性或非线性的预报建模数学方法有关联外，模型输入所包含的信息不同是否对预报模型有影响也是我们需要重点考虑的问题。一般而言，在同样的数学预报建模方法中，模型输入能包含有更多的有效预报信息，则一定能获得更好的预报效果。另一方面，目前有关神经网络集合预报方法的研究与应用在其它学科已取得了一些有效的研究成果（周志华和陈世福，2002；王正群等，2005）。而本文尝试以遗传算法与神经网络相结合的方法为基础，进行不同预报模型输入的预报建模试验研究，探索如何通过对预报因子群进行特征提取和预报因子方差贡献技术相结合的方法进行气象预报因子数据的信息挖掘，进行遗传—神经网络的台风路径集合预报模型研究。

2 基于主成分分析的遗传—神经网络集合预报模型原理和方法

由于人工神经网络的非线性气象集合预报建模方法，首先必须构造出合理的众多神经网络个体，由这些个体作集合，建立集合预报模型。为此，本文是以BP神经网络作为基本模型，进一步结合遗传算法来构建一种非线性智能计算的台风路径集合预报方法。

2.1 遗传—神经网络集合预报模型原理

2.1.1 基本模型

本文在设计采用遗传算法构建遗传—神经网络集合预报模型的集合成员个体时，神经网络的基本模型是采用一个三层BP网络，该模型的算法详见金龙等（2003）的文献，其主要计算过程可以概括为：

（1）随机给出输入层到隐层，隐层到输出层连接权和阀值，设定模型的总体收敛误差ε。

（2）根据学习矩阵样本，对网络进行有导师学习训练，计算网络的实际输入与期望输出的误差，并采用前馈网络的误差逆传播学习算法，调整输入层到隐层，隐层到输出层的连接权系数。

（3）当模型的计算输出误差＞ε时，转到（2）步，否则训练结束，并根据网络连接权、阀值和预测样本的预报因子，计算预报值。

2.1.2 编码方法

以上述三层网络为基本模型，采用二进制和实数的混合编码方法，对BP网络模型的各层节点、连接权、阀值按顺序进行编码，形成一条染色体，即遗传个体。每一个遗传个体（即每一条染色体）为一种可能的优化个体。进一步在编码空间中，随机生成一个初始的遗传种群。

2.1.3 适应度函数计算

将遗传种群（设种群的遗传个体数为m）中的遗传个体解码为神经网络的隐节点、连接权、输入训练样本计算隐层输出：

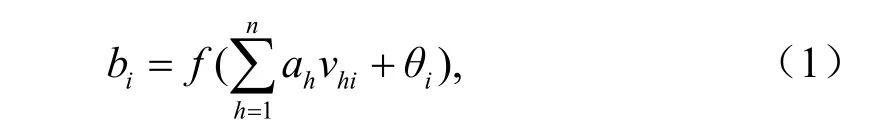
其中：i= 1,2,… ,p（其中p是隐节点个数），ah为模式输入，h=1, 2, …,n,n为输入层节点，初始时刻vhi为一组给定的随机小量，激活值函数为 sigmoid函数。计算网络输出层单元的激活值函数：

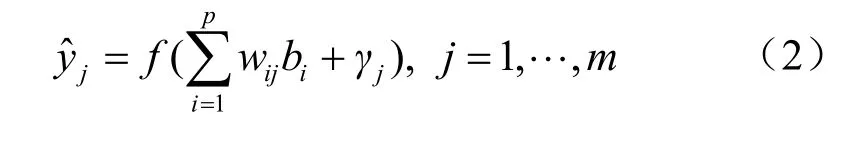
其中，vhi和wij分别为输入层至隐层和隐层至输出层的连接权系数矩阵，θi和γi分别为相应的阀值，f为转移函数。进一步计算网络的总体误差：

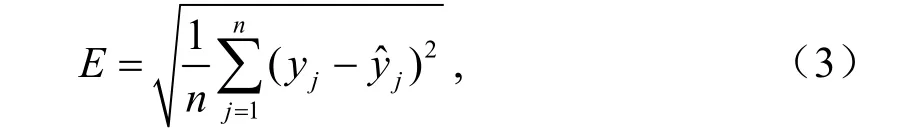
其中n为训练集样本数，定义适应度函数：可以计算出每个遗传个体的适应度。

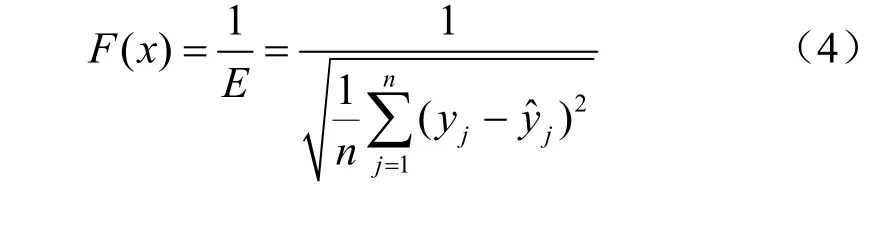
2.1.4 进化操作计算

根据遗传个体的适应度，采用选择、交叉和变异三个遗传算子对遗传种群作进化操作。其中选择算子采用轮盘选择，进一步以（5）式计算出每个遗传个体被选中的概率为：

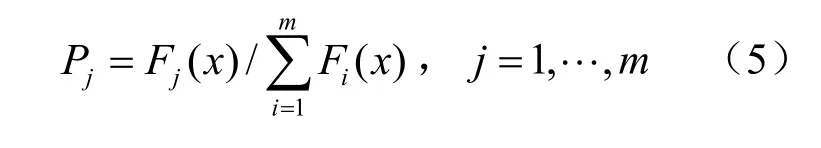
其中Fi(x)是第j个个体的适应度，m为种群的遗传个体数。使得适应度大的遗传个体能以较大概率被遗传到下一代。交叉算子以概率Pc进行多点交叉，产生新的遗传个体。变异算子则是以概率Pm对遗传个体的基因与其它遗传个体作等位的基因替换，形成新的遗传个体。如果在变异操作时，当某个遗传个体的神经元被变异删除时，则相应的有关权重系数码被设置为 0，而当变异操作运算增加某个神经元时，则随机产生有关的初始化权系数编码。

利用上述三个遗传算子进行进化操作计算从而形成新一代遗传种群。以此进行反复进化操作，每进行一次遗传操作，种群就进化一代，一直进化到N代。在进化到N代（事先设定）后，进化计算结束。将遗传种群的每一个遗传个体解码，可以得到m个神经网络模型的连接权和隐节点，从而获得可供集合预报建模的m个集合成员。对于这m个集合成员，本文将采用算术平均法对m个集合成员进行集合预报建模，即对每个神经网络个体给予相同的权重，将每个神经网络的预测值作累加得到遗传—神经网络集合预报模型的集合预报值。图1为遗传—神经网络集成预报建模流程图。

2.2 模型输入的特征提取方法

在台风路径预报中，一般能找到数目非常多的气候持续因子和动力因子，但是在实际预报中，这些方法（Jin et al.，2008；陈国良等，1995；Bessafi et al.，2002）都是采用逐步回归方法，从中选择8～10个左右的预报因子，来建立台风路径统计预报模型，而被逐步回归方法筛选、剔除的其余众多预报因子无法作为模型输入，其有用的预报信息被完全丢弃。本文尝试先用逐步回归方法对全部初选预报因子进行筛选后，进一步利用主成分分析（Principal component analysis，PCA）的特征提取方法（施能，2008），对被逐步回归方法筛选后的剩余的预报因子群进行预报信息的提取，并作为另一部分的模型输入，以改进一般集合预报模型的预报效果。

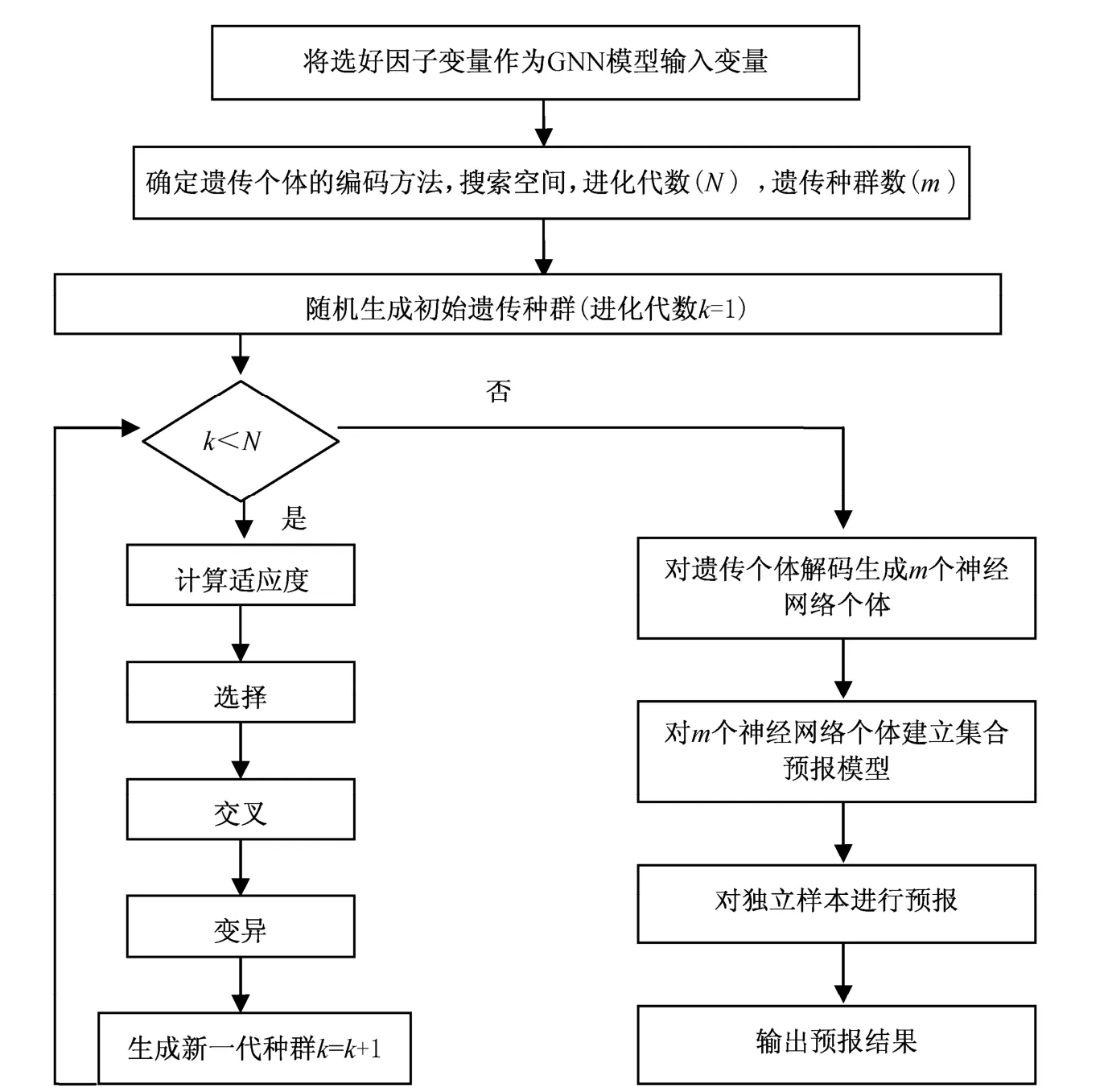
图1 遗传—神经网络方法预报建模计算流程Fig.1 Calculation process of the genetic neural network (GNN) prediction modeling

主成分分析是一种可以将多维向量空间场资料压缩到少数几个主要模态的特征提取方法，该方法已在许多学科领域得到了广泛的应用。在大气学科中，也经常利用主成分分析方法，进行天气气候特征分析及预报因子场的计算分析（周秉荣等，2009；郭品文等，2008；邓爱军等，1989）。采用主成分计算方法（施能，2008），可以将原来逐步回归筛选后的大量气候持续因子和动力因子压缩成少数几个相关系数和方差贡献及其累积方差贡献都很高的主成分因子，作为神经网络集合预报模型输入的一部分。并且由于主成分因子间是正交的，不会产生复共线性影响。

3 台风路径的人工智能预报试验

3.1 资料

在进行南海台风路径预报试验时，台风资料是采用中国气象局编辑出版的1980～2010年31年《热带气旋年鉴》资料。所讨论的南海台风是指123°E以西，10°～23.5°N的南中国海海域，盛夏的6、7、8和9月是台风最活跃的季节，因此挑选6～9月份在此海域生成或进入这一海域具有48小时以上生命史（主要是因为气候持续法预报建模需要台风前24小时的样本资料）的台风个例，并规定台风从进入该海域范围的第一点开始（在此海域生成也一样），每隔6小时作为一个统计样本。考虑到6～9月份的不同月内各气候因子对未来台风移动路径的变化均会有不同的影响，以及各月的样本个例都较多，因而采用了分月建立台风路径集合预报模型的方法。为了能对预报建模方法进行比较严格检验，统一取1980～2000年21年的台风个例用于试验的建模样本，而余下10年的台风个例则用于独立样本作预报检验。表 1为各月用于预报试验的台风个数和台风样本数。

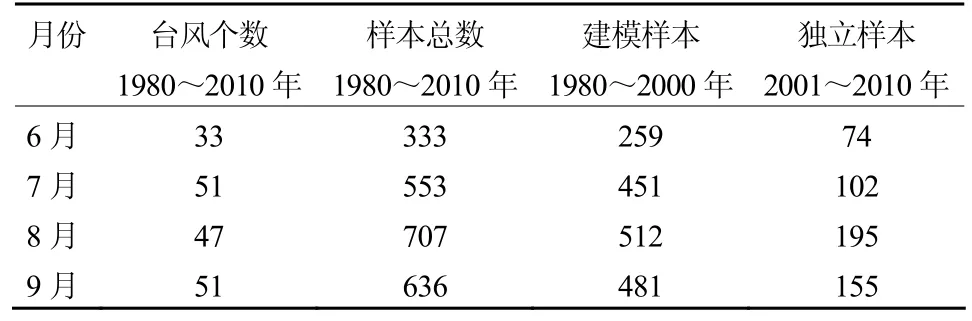
表1 1980～2010年6～9月台风个数和台风样本数Table 1 The number of typhoons and samples from June to September during 1980−2010

3.2 预报因子的初选

在采用统计预报方法进行台风路径预报时，预报因子的选择是一个重要问题，由一般的天气学分析知道，台风移动路径变化不仅受大气环流的影响，同时也与其前期位置、路径变化等诸多因素有关。由于台风路径的未来变化与台风自身前期的强度、台风所处经度、纬度及这些特征量的变化率有关，这是台风气候持续预报方法的依据。本文在建立南海台风路径预报模型时，首先是根据气候持续法原理，以相关系数达到0.15以上作为标准来选取气候持续因子，并以达到或超过0.01置信度水平作为入选标准。利用 6～9月份南海台风的建模样本资料，在实际建立预报方程时，先对南海台风的历史活动规律、初始时刻和各种前期运动特征进行详细地统计分析，进而找出影响台风未来路径的各种气候学和持续性因子。根据分析，我们采用的气候因子主要包括所在地区台风发生的频数，以及台风转向位置及其距离等等；而前期的经、纬度位置及变化，风速强度及变化等等作为重要的持续因子。

传统的台风路径统计预报方法大多是建立在各种初始因子场与台风路径的统计关系之上，而台风在移动过程中其内力及外部环境场都会发生非线性的变化，应用初始场预报因子的预报模式不能处理大气变化的非线性性质，因而预报能力较差。为此，本文在开展台风移动路径预报方法研究时，在气候持续因子的基础上，将NCEP/NCAR全球再分析资料的物理量场作为初选动力因子。数值预报产品物理量因子的选取是在台风周围 15×15个格点范围内的区域。通过与预报对象进行场相关普查，将成片（≥10个格点）稳定的高相关（相关系数≥0.3）格点作为预报因子的选择区，在区内选3个相邻格点的最大平均值作为该相关区的代表值，作为待选因子。这些动力因子主要反映台风本身内部结构变化的因子，包括：各层的垂直风切变、散度和涡度；反映环境流场与台风环流相互作用的因子，包括：水平风切变、各层高度差、温度场、高度场、东西风场、南北风场等等。

3.3 台风路径的人工智能集合预报

由于遗传—神经网络的集合预报方法本身并不具备选择因子的能力，而运用该方法进行建模预报时，模型输入因子的选择又是非常的重要，要尽可能避免不良因子的干扰，选择起关键作用的因子。逐步回归筛选出的因子建立的预测模型，具有较好的预测能力，本文首先运用回归方法选择因子。经过统计发现，6～9月份被逐步回归所选入方程的台风路径预报因子并不尽相同，而台风前期的位置及其速率等气候持续因子是最容易被选入方程的；副高对台风的移速及其转向等影响都比较大，因而动力因子中的高度场以及低层到高层的风场、涡度和散度等因子也比较容易被选入方程。

由于持续因子加上数值预报产品物理量动力因子的数量众多，经过逐步回归筛选后，剔除了大量的因子，在剩余的众多因子中，必定存在着大量对于预报量还有很大贡献的因子。为了有效利用被逐步回归方法剔除的台风预报因子所包含的预报信息，同时考虑到台风路径的预报因子的非线性性质，采用主成分分析方法对这部分被舍弃的因子进行特征提取。用主成分分析，主要是想能够用较少的综合指标（主成分）来代替多变量的因子矩阵，即达到降低维数的目的。虽然多变量样本无疑会提供更丰富的信息，但也在一定程度上增加了数据收集工作量，更重要的是由于多因子变量之间往往存在一定的相关关系、即复共线性关系，而主成分分析法的主成分是正交的。从统计学观点上看（丁裕国和吴息，1998），主成分分析方法不仅仅是正交函数逼近的问题，而且是可以从具有随机噪声干扰的气象场提取主要信号特征，排除随机干扰的统计分析方法。

本文在采用主成分分析方法对剩余因子提取主成分时，根据各个主成分与预报量的相关系数（≥0.2）及其方差贡献程度, 提取了若干个包含原数据较多信息的主成分与用逐步回归方法选入的预报因子一起作为神经网络集合预报模型的模型输入。以6月份的经度和纬度预报为例，具体做法为：

由于6月份的经度预报运用逐步回归方法已经选入了21个预报因子，还剩余93个经度预报因子，剩余因子的样本长度为259个，首先对93个剩余因子作主成分分析计算，得到93个样本长度为259的主成分（时间系数），然后加上第260个预报样本，对预报因子的260个样本进行展开，得到第260个样本的主成分，以此类推可以得到第261～333个样本的主成分。用这种方法求得的主成分具有实际预报意义，因为实际业务预报中知道的是前期预报因子的值，利用前期预报因子建立预报模型即可进行预报。通过上述主成分的计算，首先将93个主成分进行显著性检验，因为主成分分析的本质是将一个物理量场的演变分解成各正交模态的独立演变过程，故该过程就反映了各独立因子对该物理量演变的影响和贡献，一般来说，因子数量越多，主成分分析的收敛速度就越慢，对于分解出的主成分因子究竟是有物理意义的信息还是影响预报效果的噪音，应该进行显著性检验。在此采用North等（1982）提出的计算特征值误差范围的方法来进行显著性检验，经计算，93个主成分因子的前15个因子都通过了显著性检验。进一步求出通过显著性检验的各个主成分因子的方差贡献（比重），挑选出方差贡献大的前几个主成分因子与预报量（要预报的未来24小时的台风经度或纬度）进行相关计算。进一步取相关较高（≥0.2）并且方差贡献相对也较大的主成分与之前逐步回归选取的预报因子一起作为遗传—神经网络的集合预报模型的因子矩阵。这些方差贡献大且相关高的入选因子能更好地反映全部因子的预报信息，从而预报效果也会更好。对于 6月份纬度所剩余的 124个预报因子也采取同样的处理方式。这样各月所入选的主成分因子与预报量的相关情况及其方差贡献分别如表2所示。

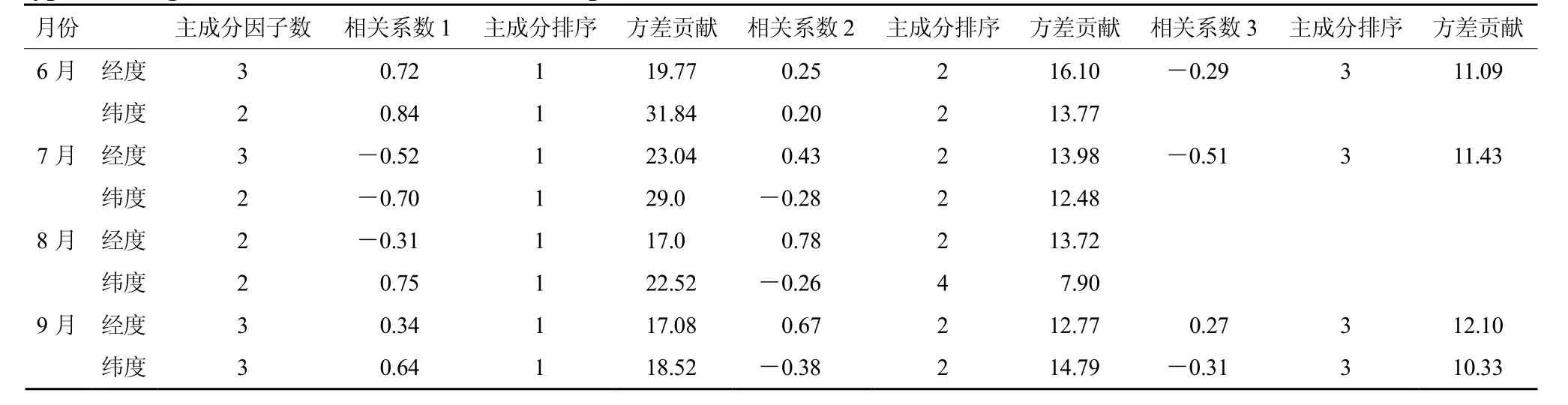
表2 6～9月台风经度和纬度入选的主成分因子相关系数及方差贡献Table 2 The correlation coefficients and variance contribution of the principal components factor selected into equations of typhoon longitude and latitude from June to September

本文在进行台风路径集合预报试验时，集合预报成员的生成是采用2.1节介绍的遗传—神经网络集合个体生成方法，分别以各月的经度和纬度选取的预报因子为基础建立相应的遗传—神经网络集合预报模型。其中遗传算法的进化计算过程中所有参数统一为：初始遗传种群数取 50，进化代数为50代。遗传操作的选择算子采用轮盘选择方法，交叉算子为多点交叉，其中控制码交叉概率取 0.9；阀值和权系数交叉概率取 0.6；变异算子为基本位变异操作，其变异概率均取0.05。神经网络的输入节点为各方程的预报因子数，输入节点为 1，并以输入节点的0.5～1.5倍作为神经网络模型结构的搜索空间，网络连接权的解空间设定为[0，1]。网络训练次数为200次，学习因子和动量因子取0.5。进化计算结束后，对50个遗传个体解码，得到50个神经网络集合预报个体。对这些集合预报个体，分别给予相同的权重，并运用算术平均法对它们进行集合预报建模，建立最终的集合预报模型。同样，利用这个集合预报模型，分别对6月份台风经度和纬度的 74个独立预报样本作预报检验。在集合预报模型对 74个独立预报样本进行预报试验时，先用259个建模样本建立预报模型对第1个独立样本作预报，然后，再以259个建模样本加上前面第1个独立样本，以260个样本作为建模样本，对第2个独立样本进行预报，……，以此类推，最后是用259加73个样本即332个样本作为建模样本对最后一个（第333个）独立样本作预报，并且所有的逐次预报中，遗传算法和神经网络的所有参数保持相同，这样可以使独立样本的预报与实际预报一致。表3为6～9月台风路径独立样本的遗传—神经网络集合预报模型的预报误差情况。

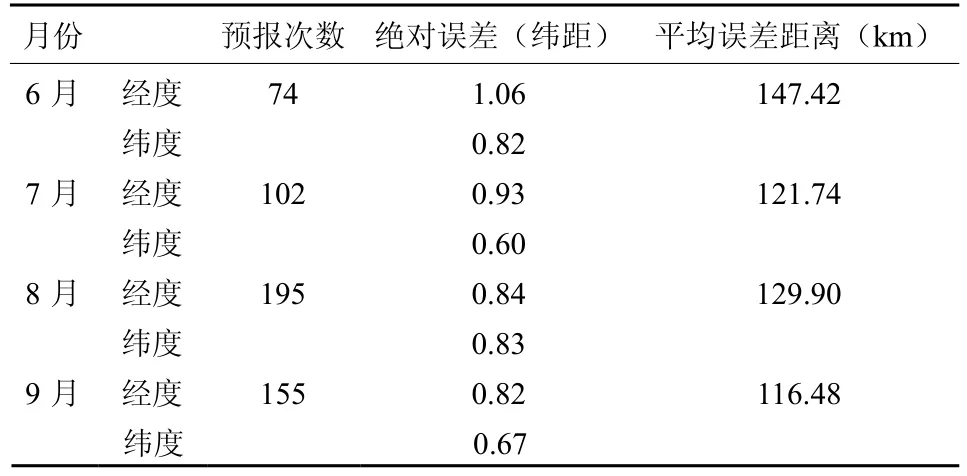
表3 遗传—神经网络集合预报模型台风路径独立预报样本的误差统计Table 3 The error statistics of typhoon track of the independent samples for ensemble prediction model

3.4 与气候持续法的对比分析

目前国内外的一些动力模式和统计—动力相结合的预报方法在台风路径的业务预报中获得了一定的成功和改进（Demarid and Kaplan，1991；吕纯濂等，1996），但是相对而言，对于台风路径的预报水平比简单的气候持续法（CLIPER或PC）改进不大（Meng et al.，2002），且台风路径的客观预报工具也不多，最普遍使用的是气候持续法。CLIPER法是一种台风移动路径预报的常用方法，它一般是以台风前期的位置和强度变化等作为主要的预报因子。本文以CLIPER法的台风预报结果作为比较对象，一则是考虑CLIPER法比较客观，没有可调参数便于比较，另外如果本文构建的这种新的人工智能集合预报方法比CLIPER法有更好的预报精度，也可以为台风路径客观预报提供新的预报工具和预报建模方法。

目前，国内外广泛采用的以台风气候持续因子建立的台风客观预报方法（Bessafi et al.，2002；Aberson et al.，2003），大多是采用回归分析方法建立预报方程。由于回归分析方法没有可调参数，建模方法客观，唯一不确定的是在面对初选得到的众多预报因子时，选取不同的F值，会有不同的预报因子组合得到相应不同的预报方程，这些不同预报方程的预报能力是有差异的。为了能进行比较客观的对比分析研究，首先根据初选得到的气候持续因子，选取与在集合预报试验中逐步回归方法所采用的同一F值来进行筛选，建立各月台风经度和纬度的气候持续预报方程，并将各月台风路径的经度和纬度预报方程分别对独立样本进行预报检验，表 4为 6～9月份台风路径独立样本的气候持续预报模型的预报误差情况。

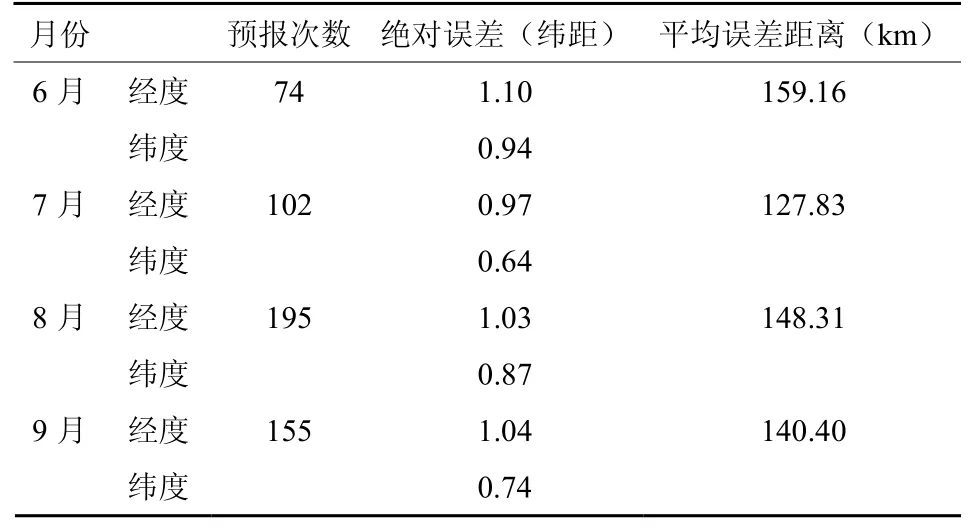
表4 气候持续预报模型台风路径独立预报样本的误差统计Table 4 The error statistics of typhoon track of the independent samples for climatology persistence (CLIPER)model

表5和图2分别是气候持续预报模式和遗传—神经网络集合预报模型 6～9月份台风移动路径独立预报样本平均绝对误差统计的结果，由统计结果的对比分析可以看出，虽然两种预报模型的预报建模样本完全相同，独立样本也完全相同，但是遗传—神经网络的人工智能集合预报模型比传统的气候持续法预报能力显著提高。进一步对各月台风路径独立样本的预报误差作统计发现，遗传—神经网络集合预报模型台风路径预报的平均绝对误差比气候持续法预报模型的预报结果明显减小，6～9月台风路径独立样本的各月预报平均绝对误差分别下降 7.4%，4.8%，12.4%，17.0%。这主要是因为气候持续法预报方程是采用线性回归分析方法建立的预报方程，而神经网络方法是一种人工智能的非线性预报建模方法，具有很强的非线性映射和自适应学习能力，可以更好地反映台风路径的非线性变化特点，而且由于加入了动力预报因子，并采用主成分分析方法进行因子选取，模型的因子矩阵具有了更为丰富的预报信息，因此独立样本预报的平均绝对误差明显下降。

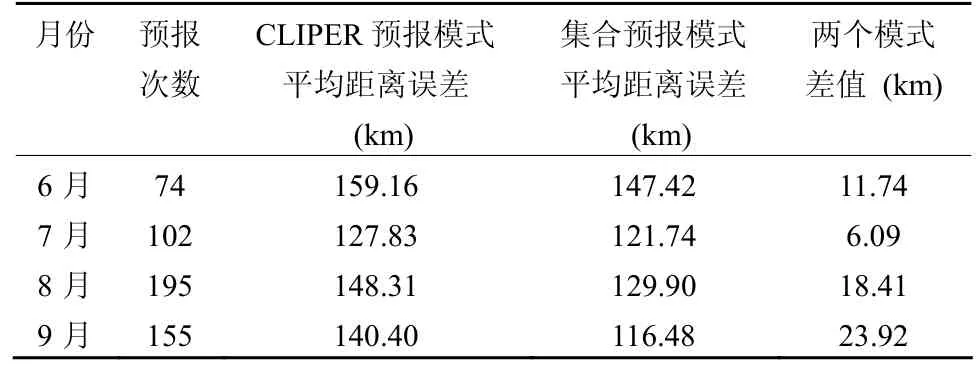
表5 集合预报模型与气候持续预报模型台风路径独立预报样本的误差统计及比较Table 5 The error statistics and comparison of typhoon track of the independent samples for GNNEP model and CLIPER model

3.5 与用主成分分析方法直接选取因子进行预报试验的对比分析

另外，为了更进一步比较本文运用逐步回归与主成分分析相结合的方法对预报因子进行处理的优越性，文章利用主成分分析的特征提取方法直接对所有初选预报因子进行选取，然后运用逐步回归和遗传—神经网络方法对同样的台风路径建模样本和独立预报样本进行计算分析。即对于各月所初选的所有气候持续因子和动力因子，直接进行主成分分析，然后完全按照上述选取主成分的原则选入主分量作为预报因子代入逐步回归方程和遗传—神经网络模型进行计算。为了客观进行对比分析，在进行计算时，和上述新方案的计算过程一样，对独立预报样本也采取了逐次计算的方式；而对于遗传—神经网络模型，其参数设置及其计算过程也完全与新方案的一致。由表6的统计结果可以看到，仅仅采用主成分分析方法选取因子所进行的两个预报试验，在初选预报因子，预报建模样本及其独立预报样本完全一致的情况下比本文新方案所预报的台风路径独立预报样本的平均绝对误差增大了很多，预报效果很差。主要是因为新方案中所运用的逐步回归方法能够比较有效地把对预报量预报贡献大的一些因子自动提取出来，对于剩下的因子，运用主成分分析方法进行主成分提取加入因子矩阵中又是一个有益的补充，因而预报效果好。

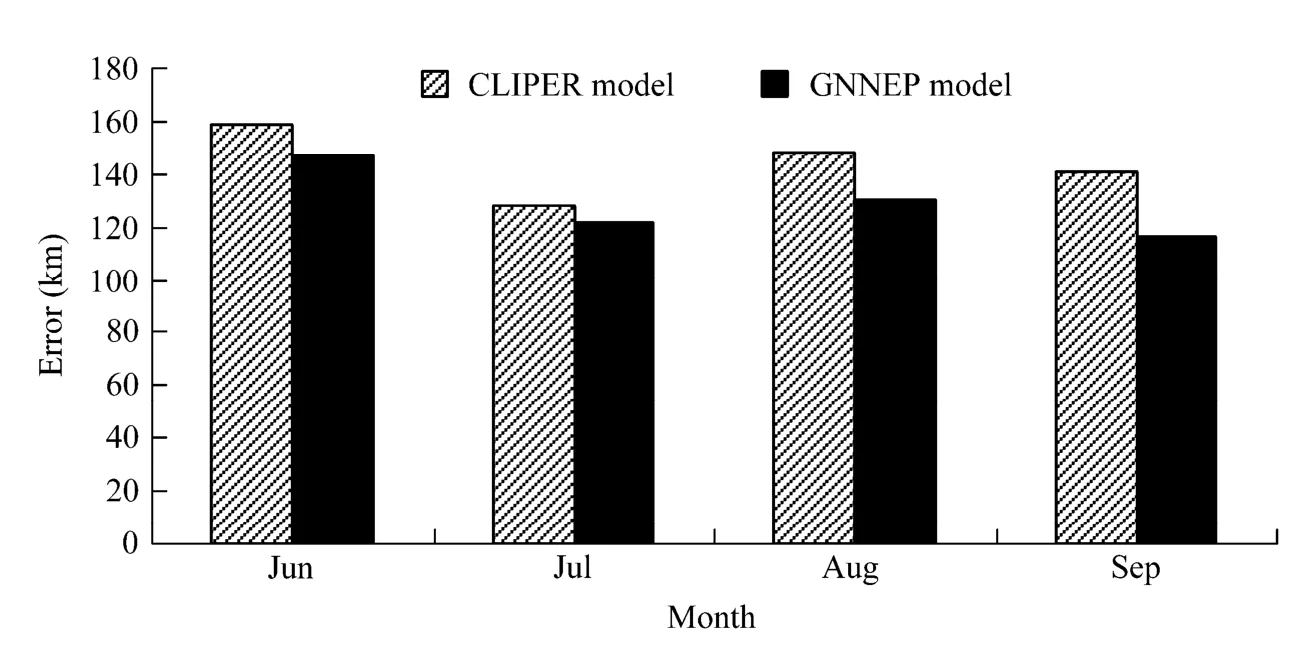
图2 2001～2010年6～9月集合预报模式与CLIPER预报模式台风独立样本预报平均绝对误差比较Fig.2 Comparison of the average absolute errors of the independent samples of the GNNEP model and CLIPER model from June to September in the period 2001−2010

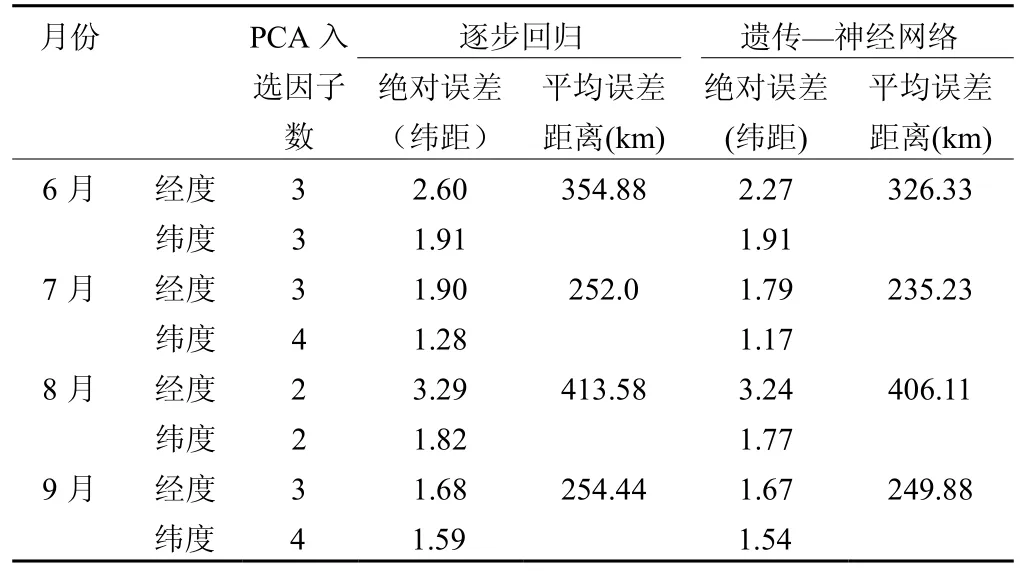
表6 主成分分析直接选因子的两个预报模型对台风路径独立样本预报的误差结果统计Table 6 The error statistics of typhoon track of independent samples of the two models which predictors was selected by PCA directly

3.6 预报技巧水平

此外，为了进一步考察这种新的遗传—神经网络集合预报模型输入构建方法，对实际业务预报是否具有预报技巧，论文运用预报技巧水平公式计算了各月预报的技巧水平（黄小燕和金龙，2007），可以得到论文所应用的新方案相对于相同时次气候持续法的预报技巧水平分别为：6月份 7.38，7月份4.76，8月份12.41，9月份17.04。可以看到，虽然用的是同一种方法，但是由于各月的入选因子不同，影响台风的各种影响要素也不同，因而各月的预报技巧水平存在差异，8月份和9月份的预报技巧相对较高，普查发现，2001～2010年的独立样本中，8月份和9月份台风的异常路径相对较多，气候持续法对于这种异常路径的预报能力一般比较弱，而本文运用遗传—神经网络方法处理这种异常路径（非线性）的能力相对较好，因而能取得更好的预报效果。进一步由图3的预报技巧水平分析得到，6～9月份基于主成分分析的遗传—神经网络集合预报模型的台风路径预报的预报技巧相对于气候持续法均为正的预报技巧水平，说明新的模型具备一定的预报能力，而且本文在建立遗传—神经网络的集合预报模型时，所有参数都取固定，从而使预报具有很好的客观性。

3.7 实际预报

在新模型对 2001～2010年所有的独立样本进行实际预报检验中，我们挑选了其中的两个台风个例来进行分析。0907号台风 “Goni” 于 2009年 7月 31日 20时在南海生成，是较为典型的异常路径，它在广东沿海登陆后发生转向进入了北部湾海面，此后一直绕着海南岛西面行进，此转向路径给实际预报造成了一定的困难，从图4的台风 “Goni”预报路径与实况的比较图来看，本文运用的新模型对此转向台风有一定的预报能力，转向的趋势基本上都能预报出来，误差较小。

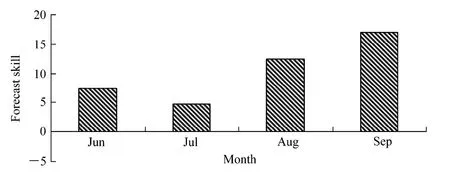
图3 2001～2010年6～9月台风集合预报模式相对于气候持续法的预报技巧水平Fig.3 The forecast skill of the GNNEP model relative to the CLIPER model from June to September in the period 2001−2010

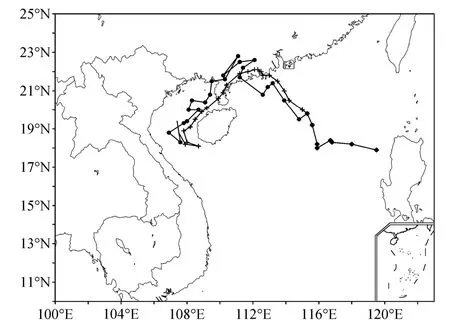
图4 0907台风 “Goni” 预报路径与实况的比较（加黑点标志为实况路径，加“+”标志为预报路径）Fig.4 Comparison of the forecasted and observed paths of typhoon 0907“Goni” (line with dots is the observed path, line with “+” is the forecast path)

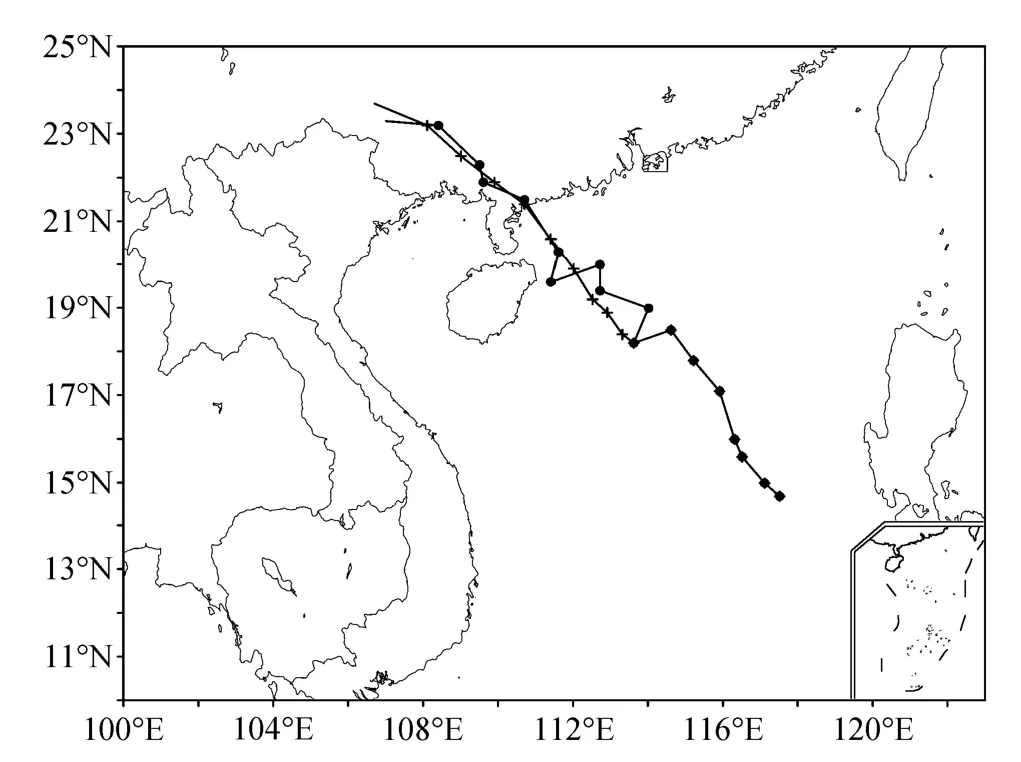
图5 1003号台风 “灿都” 预报路径与实况的比较（加黑点标志为实况路径，加 “+” 标志为预报路径）Fig.5 Comparison of the forecasted and observed paths of typhoon 1003“Chanthu” (line with dots is the observed path, line “+” is the forecast path)

图5是1003号台风 “灿都” 预报路径与实况的比较图，“灿都” 路径呈西北走向，稳定少动，它在广东廉江市登陆后，继续西北行进入广西，进而在广西百色市境内减弱消失，这样的路径，一般在南海台风中是比较多见的。从图中可以看到，新模型的预测能力也较好，台风登陆地点预报准确，整个路径的预报误差控制在较少的范围内。

进一步由表7的三种预报模型对这两个台风预报的结果进行对比分析得到，新模型对 0907号台风的预报是从8月3日02时开始的，每隔6小时进行预报，共23次，模式的预报误差约为95.93 km，运用气候持续法对同样的台风样本进行预报，结果为136.93 km，比新模型的预报误差增加了41 km；而直接采用主成分分析方法选择因子进行的预报结果为170.64km，误差比新模型增加了近一倍，预报效果较差，与试验结果一致。另外，三种预报模型对 1003号台风的预报结果也同样如此，其中的新模型预报误差相对都是最小的。从比较的结果可以得出，新模型对的预报能力较其它两种方法的预报能力明显偏高。

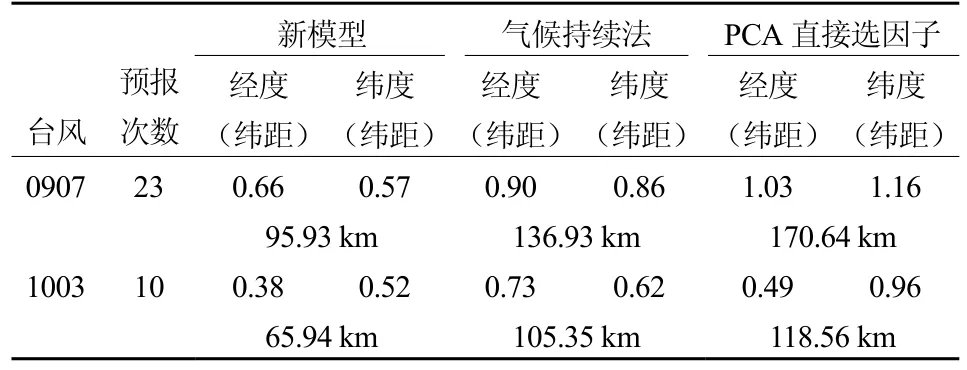
表7 三种预报模型分别对0907、1003号台风的实际预报结果Table 7 The actual forecast results of typhoons 0907 and 1003 by three typhoon forecasting models

4 小结

（1）一般的统计预报建模方法预报效果的好坏，很重要的是取决于预报因子的选取，即这些因子是否真正能从多方面来反映与预报量的关系。本文在台风路径的因子初选中，基于各种影响要素的考虑，在传统考虑的气候持续因子的基础上，加入了数值预报产品动力预报因子，这既包含了反映预报量前期的强度、位置变化等重要因素，又包含了大气环境场物理量中对预报量有影响的外部因子，从而在因子矩阵中增加了更为丰富的预报信息。

（2）由本文给出的南海台风路径短期天气预报的遗传—神经网络集合预报模型，在初选预报因子、预报建模样本数及遗传进化计算所有参数、神经网络模型训练次数等完全相同的情况，对多模型大样本的台风路径集合预报试验结果表明，通过对逐步回归方法选择预报因子后，再对剔除的预报因子采用主成分分析提取与预报量相关高的特征分量作为另一部分模型输入，可以充分有效地挖掘全部预报因子的预报信息。并且由于用主成分分析，可以对原数量较多的相关预报因子作有效的降维处理，将原因子场的有效预报信息浓缩到与相关较高并且方差贡献大的少数几个主分量上。以这样的主分量加入预报模型，不仅可以构造较小的网络结构，同时也不丢弃任何有效的预报信息，从而可以有效提高神经网络预报模型的预报精度。

（3）遗传—神经网络集合预报模型的是由多个神经网络个体预报结果合成，而神经网络方法是一种人工智能的非线性预报建模方法，具有很强的非线性映射和自适应学习能力，可以更好地反映台风路径的非线性变化特点。集合模型的各个神经网络个体的网络结构，是通过遗传算法的优化计算确定的，因此，该集合预报模型的泛化能力显著提高，具有较好的实用性和推广价值。

（4）在建模样本数，独立预报样本完全相同的情况下，本文新方案对各月台风路径的预报精度不仅比传统的气候持续法预报方程有显著提高，而且比直接运用主成分分析方法选取因子直接进行逐步回归和遗传—神经网络计算也有明显改进。另外，通过计算表明，新方案对各月的预报均为正的预报技巧水平，实际预报也显示了较好的预报效果，说明该方法有直接进行业务应用预报的能力。

（References）

Aberson S D, Sampson C R.2003.On the predictability of tropical cyclone tracks in the Northwest Pacific basin [J].Mon Wea Rev, 131 (7):1491–1497.

Bessafi M A, Lasserre-Bigorry C J, Neumann F, et al.2002.Statistical prediction of tropical cyclone motion: An analog-CLIPER approach [J].Wea.Forecasting, 17: 821–831.

陈刚毅, 丁旭羲, 赵丽妍.2005.用模糊神经网络自动识别云的技术研究 [J].大气科学, 29 (5): 837–844.Chen Gangyi, Ding Xuxi, Zhao Liyan.2005.An automatic pattern recognition techniques of cloud based on fuzzy neural network [J].Chinese Journal of Atmospheric Sciences (in Chinese), 29 (5): 837–844.

陈国良, 王熙法, 庄镇泉, 等.1995.遗传算法及其应用 [M].北京: 人民邮电出版社, 28–127.Chen Guoliang, Wang Xifa, Zhuang Zhenquan,et al.1995.Genetic Algorithms and Its Application (in Chinese) [M].Beijng: People’s Posts and Telecommunications Press, 28–127.

Demarid M, Kaplan J.1991.A statistical model for predicting tropical cyclone intensity change [C] //19th Conference on Hurricanes and Tropical Meteorology.Miami, Florida, AMS, 521–526.

丁裕国, 吴息.1998.经验正交函数展开气象场收敛性的研究 [J].热带气象学报, 4 (4): 316–326.Ding Yuguo, Wu Xi.1998.Study the convergence for the expansion of meteorological fields with empirical orthogonal functions [J].Journal of Tropical Meteorology (in Chinese), 4(4): 316–326.

丁裕国, 程正泉, 程炳岩.2002.MSSA-SVD典型回归模型及应用于ENSO 预报的试验 [J].气象学报, 60 (3): 361–369.Ding Yuguo,Cheng Zhengquan, Cheng Bingyan.2002.A prediction experiment by using the generalized canonical mixed regression on model based on MSSA-SVD for ENSO [J].Acta Meteorologica Sinica (in Chinese), 60(3): 361–369.

邓爱军, 陶诗言, 陈烈庭.1989.我国汛期降水的EOF分析 [J].大气科学, 13 (3): 289–295.Deng Aijun, Tao Shiyan, Chen Lieting.1989.The EOF analysis of rainfall in China during monsoon season [J].Chinese Journal of Atmospheric Sciences (in Chinese), 13 (3): 289–295.

郭品文, 居丽丽, 徐同.2008.非线性主成分分析在中国四季降水异常分布中的应用 [J].南京气象学院学报, 31 (4): 460–467.Guo Pinwen,Ju Lili, Xu Tong.2008.Application of nonlinear principal component analysis to seasonal precipitation anomaly over China [J].Journal of Nanjing Institute of Meteorology (in Chinese), 31 (4): 460–467.

郭章林, 刘明广, 解德才.2004.震灾经济损失评估的遗传神经网络模型 [J].自然灾害学报, 13 (6): 92–96.Guo Zhanglin, Liu Mingguang,Xie Decai.2004.Genetic algorithm-neural network-based economic losses assessment of seismic disaster [J].Journal of Natural Disasters (in Chinese), 13 (6): 92–96.

Haupt S E, Young G S, Allen C T.2006.Validation of a receptor-dispersion model coupled with a genetic algorithm using synthetic data [J].Journal of Applied Meteorology and Climatology, 45 (3): 476–490.

哈斯巴干, 马建文, 李启青, 等.2004.容差粗糙集与神经网络结合的遥感数据分类方法 [J].中国科学D辑, 34 (10): 967–974.Hasi Bagan,Ma Jianwen, Li Qiqing, et al.2004.Classification the remote sensing data with the method of combined the tolerance rough set and neural network[J].Science in China Series D (in Chinese), 34 (10): 967–974.

黄小燕, 金龙.2007.条件数在台风移动路径预报中的应用 [J].自然灾害学报, 16 (3): 35–40.Huang Xiaoyan, Jin Long.2007.Application of condition number in forecasting typhoon motion [J].Journal of Natural Disasters (in Chinese), 16 (3): 35–40.

胡娅敏, 丁一汇, 沈桐立.2006.基于遗传算法的四维变分资料同化技术的研究 [J].大气科学, 30 (2): 248–256.Hu Yamin, Ding Yihui,Shen Tongli.2006.A research of four-dimensional variational dataassimilation based on genetic algorithm [J].Chinese Journal of Atmospheric Sciences (in Chinese), 30 (2): 248–256.

洪梅, 张韧, 吴国雄, 等.2007.用遗传算法重构副热带高压特征指数的非线性动力模型 [J].大气科学, 31 (2): 346–352.Hong Mei, Zhang Ren, Wu Gguxiong, et al.2007.A non-linear dynamic system reconstruction of the subtropical high characteristic index based on genetic algorithm [J].Chinese Journal of Atmospheric Sciences (in Chinese), 31 (2): 346–352.

金龙, 秦伟良, 姚华栋.2000.多步预测的小波神经网络预报模型 [J].大气科学, 24 (1): 79–86.Jin Long, Qin Weiliang, Yao Huadong.2000.A multi-step prediction model of wavelet neural network [J].Chinese Journal of Atmospheric Sciences (in Chinese), 24 (1): 79–86.

金龙, 罗莹, 李永华.2003.长期天气的人工神经网络混合预报模型研究 [J].系统工程学报, 118 (4): 331–336.Jin Long, Luo Ying, Li Yonghua.2003.Study on mixed prediction model of artificial neural network for long-range weather [J].Journal of Systems Engineering (in Chinese), 118 (4): 331–336.

Jin L, Yao C, Huang X Y.2008.A nonlinear artificial intelligence ensemble prediction model for typhoon intensity [J].Mon Wea Rev, 136: 4541–4554.

金一鸣.1983.多预报量双重筛选逐步回归在台风路径预报中的应用[J].大气科学, 7 (2): 235–238.Jin Yiming.1983.Double filter the many predictors by stepwise regression for typhoon tracks forecasting [J].Chinese Journal of Atmospheric Sciences (in Chinese), 7 (2): 235–238.

李爱军, 李贺军, 李克智, 等.2003.C/C复合材料CVI工艺人工神经网络建模 [J].中国科学E辑, 33 (3): 209–216.Li Aijun, Li Hejun, Li Kezhi, et al., 2003.Modeling of isothermal CVI process of C/C composites by artificial neural network [J].Science in China (Series E)(in Chinese), 33 (3): 209–216.

刘妹琴.2005.离散时滞标准神经网络模型及其应用 [J].中国科学E辑,35 (10): 1031–1048.Liu Meiqin.2005.Standard discrete time-delay neural network model and its application [J].Science in China Series E(in Chinese), 35 (10): 1031–1048.

吕纯濂, 陈舜华, 朱永提.1996.多维动态关联模型在台风路径、强度和风速同时预报中的应用研究 [J].气象学报, 54 (6): 737–744.Lü Chunlian, Chen Shunhua, Zhu Yongti.1996.Research and apply multiple dynamic interdependent model (MDIM) to predict typhoon track、intensity and wind-speed [J].Acta Meteorologica Sinica (in Chinese), 54(6): 737–744.

倪允琪, 金汉良, 薛家元.1981.西太平洋台风路径业务数值预告模式及其初步使用结果 [J].大气科学, 5 (3): 281–291.Ni Yinqi, Jin Hanliang, Que Jiayuan.1981.An operational numerical forecasting scheme of typhoon tracks over the western Pacific and its preliminary results [J].Chinese Journal of Atmospheric Sciences (in Chinese), 5 (3):281–291.

Meng Z Y, Chen L S, Xu X D.2002.Recent progress on tropical cyclone research in China [J].Advances in Atmospheric Science, 19 (1): 103–110.

North G R, Bell T L, Cahalan R F, et al.1982.Sampling errors in the estimation of empirical orthogonal function [J].Mon Wea Rev, 110:699–706.

施能.2008.气象科研与预报中的多元分析方法 [M].北京: 气象出版社, 72–114.Shi Neng.2008.Multiple Analysis Method in Scientific Research and Forecast of Meteorology (in Chinese) [M].Beijing: China Meteorological Press, 72–114.

王正群, 陈世福, 陈兆乾.2005.并行学习神经网络集成方法 [J].计算机学报, 28 (3): 402–408.Wang Zhengqun, Chen Shifu, Chen Zhaoqian.2005.A parallel learning approach for neural network ensemble [J].Chinese Journal of Computers (in Chinese), 28 (3): 402–408.

魏鼎文, 张捷迁.1978.台风路径的某些模拟实验研究 [J].大气科学, 2(3): 290–296.Wei Dingwen, Zhang Jieqian.1978.Some of the simulation experiment for typhoon tracks [J].Chinese Journal of Atmospheric Sciences (in Chinese), 2 (3): 290–296.

严军, 刘健文.2005.基于神经网络奇异谱分析的 ENSO 指数预测 [J].大气科学, 29 (4): 620–626.Yan Jun, Liu Jianwen.2005.A study of ENSO index prediction based on neural network singular spectrum analysis [J].Chinese Journal of Atmospheric Sciences (in Chinese), 29 (4):620–626.

张韧, 洪梅, 王辉赞, 等.2008.基于遗传算法优化的ENSO指数的动力预报模型反演 [J].地球物理学报, 51 (5): 1346–1353.Zhang Ren,Hong Mei, Wang Huizhan, et al.2008.Retrieval of the non-linear dynamic forecast model of El Nino/La Nina index based on the genetic algorithm optimization [J].Chinese Journal of Geophysics (in Chinese),51 (5): 1346–1353.

Zheng Deling, Liang Ruixin, Zhou Ying, et al.2003.A chaos genetic algorithm for optimizing an artificial neural network of prediction silicon content in Hot Metal [J].Journal of University of Science and Technology Beijing, 10 (2): 68: 68–71.

周家斌, 黄嘉佑.1997.近年来中国统计气象学的新进展 [J].气象学报,55: 297–305.Zhou Jiabin, Huang Jiayou.1997.The new development of meteorology in recent years in China [J].Acta Meteorologica Sinica (in Chinese), 55: 297–305.

周秉荣, 李凤霞, 申双和, 等.2009.从MODIS资料提取土壤湿度信息的主成分分析方法[J].应用气象学报, 20 (1): 114–118.Zhou Bingrong, Li Fengxia, Shen Shuanghe, et al.2009.Principal component analysis method acquiring soil moisture information from MODIS data[J].Journal of Applied Meteorological Science (in Chinese), 20 (1):114–118.

周志华, 陈世福.2002.神经网络集成 [J].计算机学报, 25 (1): 1–8.Zhou Zhihua, Chen Shifu.2002.Neural network ensemble [J].Chinese Journal of Computers (in Chinese), 25 (1): 1–8.