基本气流和边界层顶高度对低纬大气数值模拟的影响

王鹏飞 黄平 顾雷 黄荣辉

1中国科学院大气物理研究所季风系统研究中心，北京100190

2中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京100029

3中国民用航空局空中交通管理局航空气象中心，北京100122

1 引言

热带大气中水汽充足，经常处于不稳定状态，积云对流活动频繁，对流导致的加热反馈成为热带大气运动的重要物理过程。Madden and Julian（1971）通过资料分析指出赤道附近存在大气低频振荡，但未做动力学研究，Lindzen（1974）提出了波动—CISK（Convective Instability of the Second Kind）理论，Chang（1977）认为热带大气低频振荡可以用粘性重力内波做动力学解释，Lau and Chan（1985）使用资料分析研究了低频振荡的性质，进而 Lau and Peng（1987）引入了动力学模型对其进行了研究。Hayashi（1970）与 Takahashi（1987）研究了热带对流反馈对热带大气的 30～60天振荡的激发作用。李崇银（1985）把CISK机制引入30～60 天振荡起源的研究, 并定义为移动 CISK波；Huang（1994）研究了30～60 天振荡、沃克环流和北半球夏季热带西太平洋对流活动之间的关系，指出 30～60天振荡的年际变化与热带西太平洋的对流活动紧密相关。

Miyahara（1987）所使用的 CISK机制的数值模式是研究热带地区的低频振荡的结构、特征和激发机制的一种常用模式，他的模拟结果表明了外源强迫对激发大气低频振荡的重要性，得到了 20天左右的周期低频振荡。刘爱弟和黄荣辉（1994）用此模式研究了热带大气 30～60天振荡的动力学机制，通过改变加热分布形式、设置快变热源与缓变热源，发现热带大气 30～60天振荡是大尺度环流与热带对流活动相互作用产生的，对流活动对热带大气 30～60天振荡有着重要影响；崔雪峰和黄荣辉（2002）通过改变热源位置和大小，分别放在热带太平洋、热带印度洋进行了数值试验，发现热源的纬向位置没有明显影响，而尺度大小对振荡的周期有影响；顾雷（2006）将热源位置放在热带西太平洋，进而研究了低频振荡和南海季风进退之间的关系。

另外一些研究者通过简化模型，从理论上分析了流场切变等对低频振荡的影响（赵强和刘式适，2001）。沈新勇等（2006）的研究结果表明，基本气流的水平切变对赤道大气波动起到促进不稳定发生的作用，但是对赤道大气Kelvin波的频率、稳定性以及传播的相速度并不起作用。基本气流的水平切变使得相对于基本气流向东传播的重力波相速度减慢，同时使得相对于基本气流向西传播的重力波的相速度加快，而且造成相对于基本气流向西传播的 Rossby波相速度减慢。基本气流的水平切变对于对赤道混合 Rossby—重力波的影响主要取决于纬向波数值的范围大小。当纬向波数k值较小时，基本气流的水平切变使得相对于基本气流向西传播的混合Rossby—重力波相速度加快；而当纬向波数k值较大时，则使得相对于基本气流向西传播的混合Rossby—重力波相速度减慢。巢纪平（2009）的书中较全面地回顾了基本流对赤道波动的影响，指出当扰动在背景场中发展时，扰动场和背景场的非线性作用可以将扰动的动量通量转换为背景场的动量，从而改变背景场的平均流速，或其他物理量。

数值结果表明低频振荡的周期和激发机制中仍存在不确定性，而其中参数化项——边界层顶的高度误差对低频振荡的数值模拟是否会产生影响尚无明确的结论。水平基本气流对低频振荡的影响已经有了一些使用简化模式的理论推导，但是这些研究所用的模型较简单，没有考虑水平扩散和垂直扩散的因素，也没有经过数值试验的验证。因此，能否在 Miyahara模型的基础上通过数值模拟来研究对流热源与基本气流的相互作用，是一个很有意义的科学问题。

2 热带含CISK机制的模式方程组和有关参数

2.1 模式方程组

Miyahara（1987）模式方程如下：

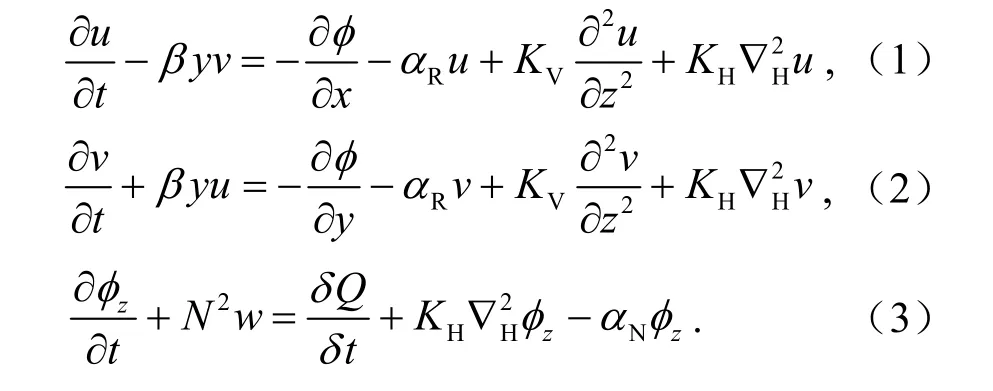
此模式在垂直方向使用的是对数压力坐标z=-Hln(pp0)，当基态取为等温大气时（在等温大气中对数压力坐标和普通z坐标相等），利用等温大气中的密度关系ρ=ρ0exp(-zH)，可以将连续方程写为：

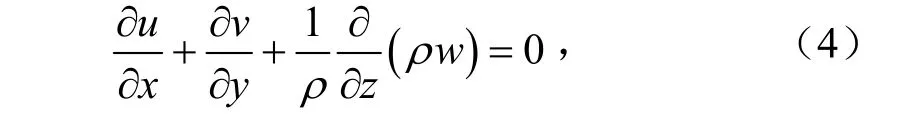
其中公式（3）是由静力平衡关系∂φ∂z=RTH和热力学方程：

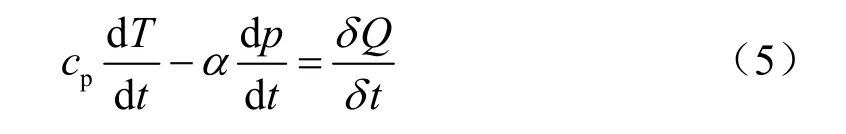
（含扩散项的形式为：∂T/∂t+N2w=1/cpδQ/δt+K-αNT）联立得到。方程中，u，v分别代表扰动风场的纬向和经向分量，φ为高度场，w代表垂直扰动运动,φz=∂φ∂z，αR和αN分别为Rayleigh摩擦系数和牛顿冷却系数，本文中αR=αN=4.8×10-6s-1，N是布伦特—维亚赛拉频率，取为常数 (1.0×10-2s-2)，KH、KV分别为水平和垂直扩散系数，分别取为1.0×106m2s–1和5.0 m2s–1，β取2.28×10-11，Q为热源强迫。

公式（1～4）共 4个方程，求解的变量为u,v,w,φ，方程组是闭合的，一般只能用数值方法求解。

为了在热力学方程公式（3）中引入 CISK机制，把热源强迫项分成外部强迫热源KJ/H和对流活动产生的潜热热源两部分。对于对流活动所产生的潜热用一个简单的参数化方案表示，即设它和边界层顶的垂直速度成正比，这样，热力学方程可写为：

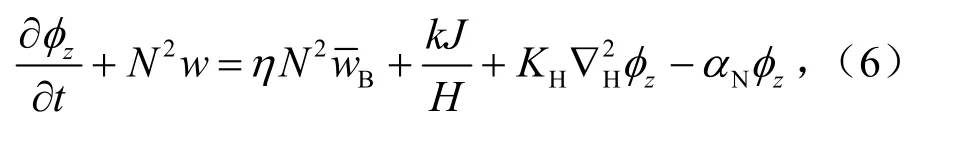
其中H是模式中大气层高度，计算中取H=7994 m；η(x,y,z)是CISK机制的比例参数；k=R/cp=0.286，R是气体常数。

2.2 有关参数

由于高海温（SST）区域的对流活动比低 SST区域的对流活动强, 因而与凝结过程有关的内部加热在高SST区域也要比低SST区域的强, 它在印度洋到赤道中太平洋地区是比较强的。故取内加热（即由对流活动引起的加热）的参数为：

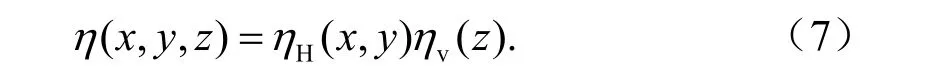
水平加热量ηH(x,y)的表达式为：

式中取a=15000 km，b=4000 km，c=13000 km，即强对流活动区域位于赤道印度洋和赤道西太平洋上空，并取为对赤道对称，而垂直加热参量ηv(z)用下面公式计算:

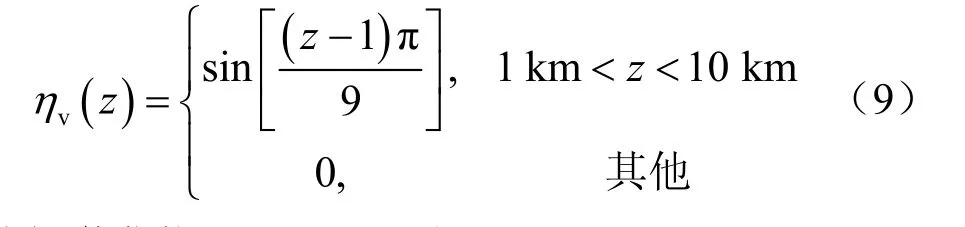
外部激发热源J可以写成：

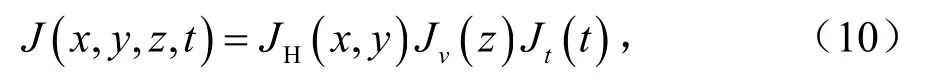
其中

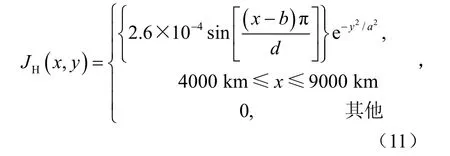
d=5000 km，即外部触发热源位于赤道西印度洋（经度约40°～90°E），取关于赤道对称。对系统而言，它是一个比内部热源要小得多的触发热源，定期对大气进行扰动。为了方便研究，外部热源的垂直结构取成与内部热源相同，即Jv(z) =ηv(z)。Jt(t)表示触发热源随时间的分布, 设它随时间呈周期性振荡, 取周期为4 d，这比大气季节内振荡的周期要小的多，公式为：

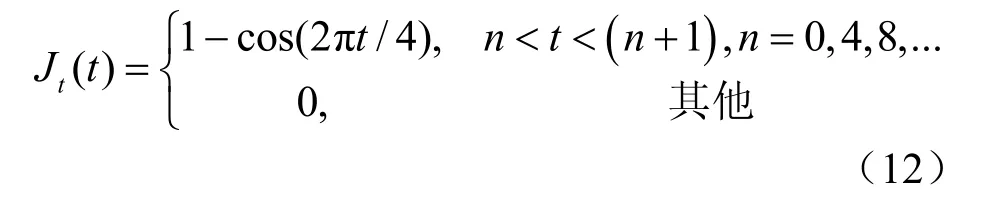
模式积分的范围为经向从32°S到32°N，纬向从0°到 360°E，水平网格间距 Δx=625 km,Δy=440 km, Δt= 600 s在垂直方向上用如下转换公式把大气分成10层。

表1 每一层在z坐标中的高度值Table 1 The height of vertical level in z coordinate

其中，H0=1.0 km ，r=0.34，垂直间距Δζ=1.0，模式每一层在z坐标系中的高度见表1。

模式中w的计算位于两层的中间，(x,y)是边界层顶（这里取边界层顶z=1.03 km）垂直速度进行平滑得到的平均值。

2.3 边界条件和积分方案

在模式中，积分区域假定为一个沿x方向延伸的通道，东西方向 65个格点，周期边条件；南北方向17个网格点，而在边界y=±3520 km即32°S和32°N处取为刚壁条件。

当z= 0时，模式的底边界取为：

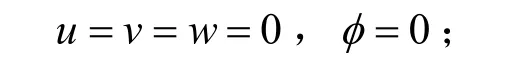
当z= 28.96 km 时，模式上边界条件取为：

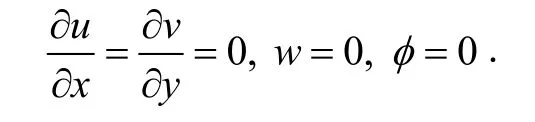
方程（1）、（2）、（3）、（6）的时间积分方案采用如下差分格式:

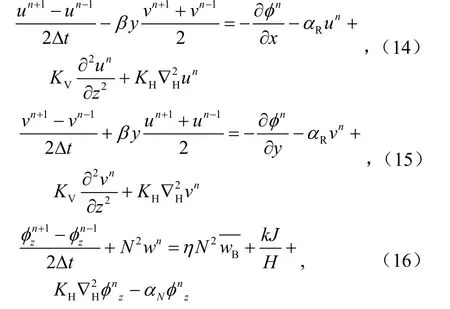
其中un表示第n个时间点上的数值，时间步长为600 s。模式选取了三时间层的蛙跳格式，将科氏力项写为隐式，但仍能够显式求解，由于引入了三时间层的格式，所以加入了时间滤波，模式启动时，风场和位势场的初值取为零。模式以 Fortran语言编写，调用Netcdf库，输出文件为nc格式。

图1中给出了模式计算100天所得到的u风场和边界层顶的垂直速度扰动传播，可以看到，模式基本能够模拟出 50～60天的周期振荡现象，说明模式运行正确，可以用来进行下一步的试验。

3 基本气流的作用

3.1 方程组的变化

本节在公式（1）、（2）、（6）、（4）的基础上研究基本气流的影响，加入东西方向且定常的基本气流（参照沈新勇等，2006），扰动项的形式变为：

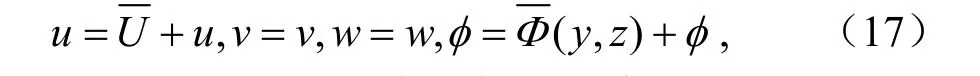
假定小扰动和基本态都满足静力平衡，且满足地转平衡，利用关系式：

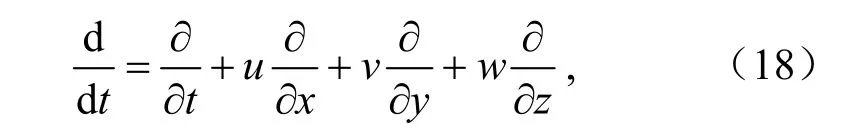
以及=-∂∂y，可以得到加入基本气流后的扰动方程组为：

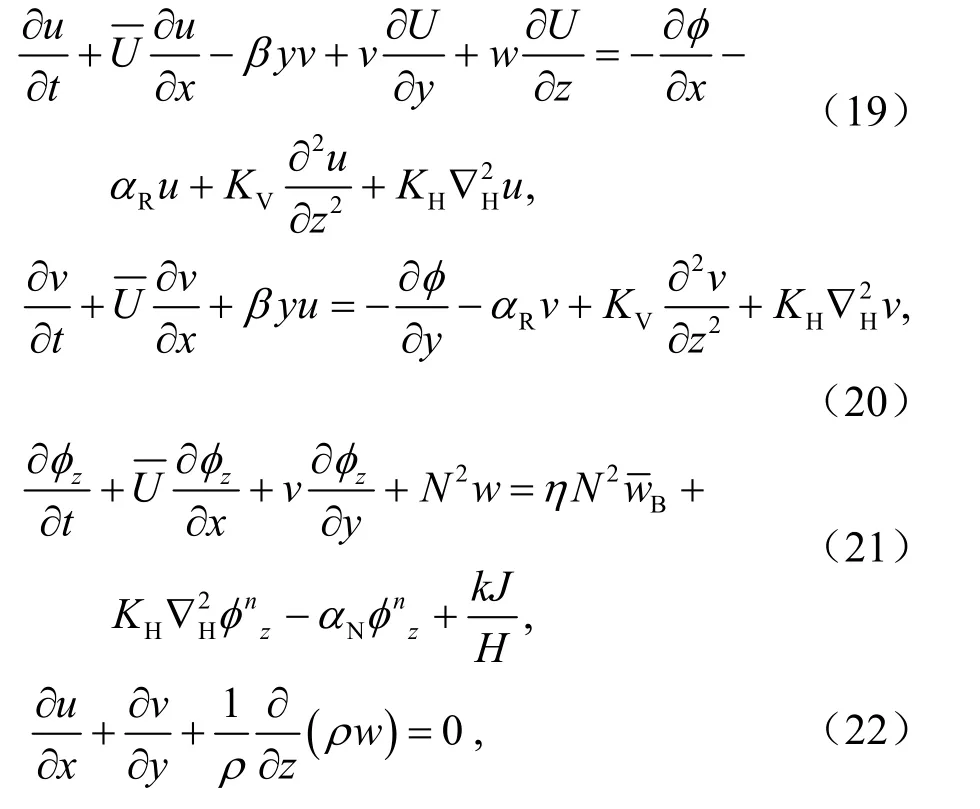
若的分布与y,z无关，式（19）化为：

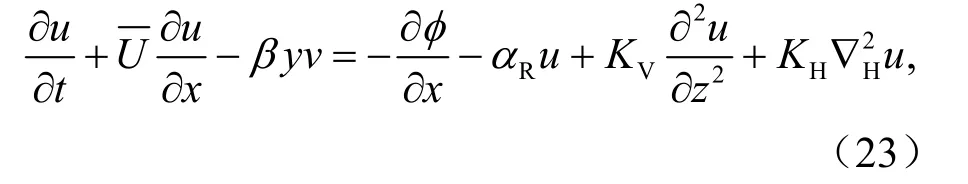
而式（21）中的v∂φy=v∂2∂z=(∂),利用地转平衡关系：∂=，可得v∂∂y=vβyz。因此, 式（21）化为：

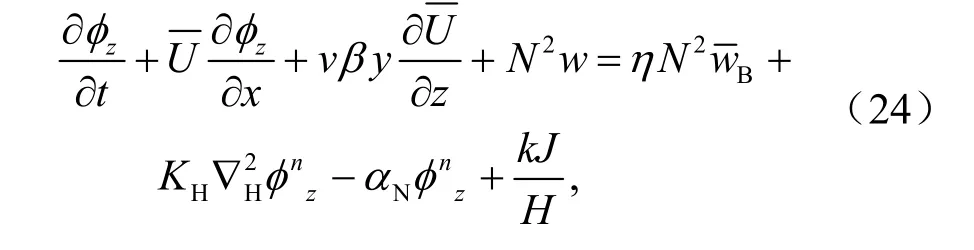
因的分布与 ,yz无关，式（24）可进一步化为：

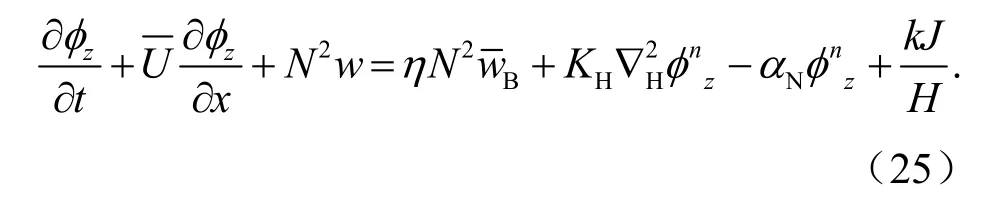
计算时，选取=常数（为了书写方便，以下以U代替），然后用（23）、（20）、（22）、（25）所构成的方程组进行模拟。

3.2 低频振荡的变化

图2为加入了水平流场后，模式计算100 d所得到的风场和边界层顶的垂直速度扰动传播，可见模拟出的振荡周期与图1相比发生了显著变化，振荡周期有缩短的趋势，为 30天左右的周期，这表明基本气流和对流潜热的相互作用可以改变低频振荡的性质。

图 3为进一步改变水平风速，当U=－1 m/s（东风）时得到的一个扰动发展图，可见当水平风速为东风时，振荡周期有加大的趋势，甚至可达70～80 d。

表2中列出了一些基于Miyahara (1987) 模式的研究中所使用的计算参数和得到的振荡周期、发生时间等结果，从表中的数据可以发现计算参数的选取对结果影响比较显著。

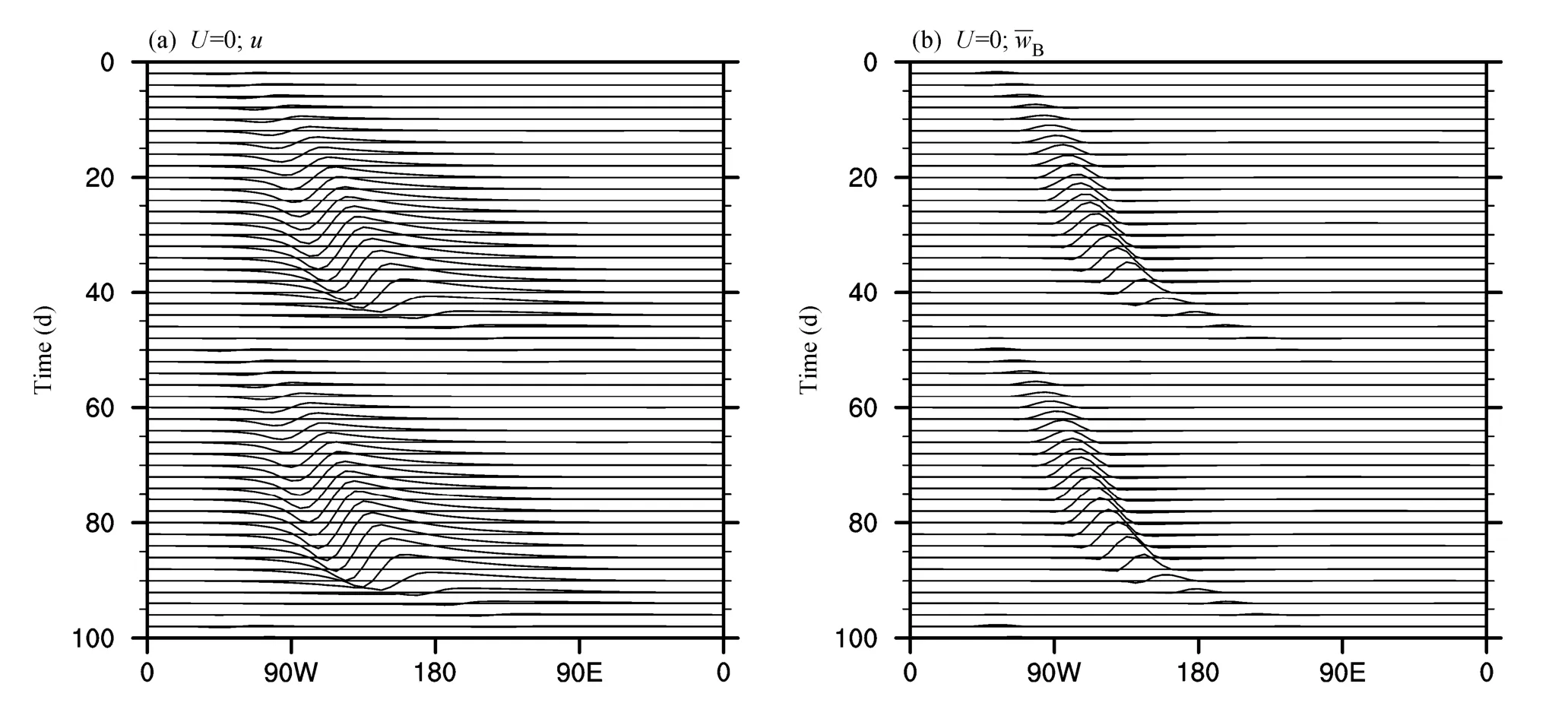
图1 （a）赤道上空9.8 km处每两天的纬向风u随经度的分布；（b）赤道上空1.03 km处每两天的垂直速度随经度的分布Fig.1 (a) The horizontal wind speed uversus longitude, the time interval is 2 d and the vertical level is at 9.8 km above the equator; (b) the verticalwind speed versus longitude, the time interval is 2 d and the boundary layer top is at 1.03 km above the equator

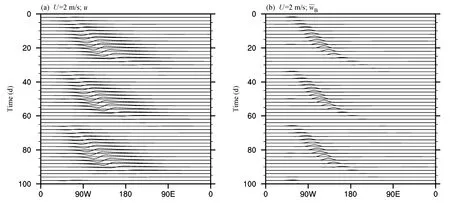
图2 当水平风速U=2 m/s时模拟得到的数值解：（a）赤道上空9.8 km处每两天的纬向风u随经度的分布；（b）赤道上空1.03 km处每两天的垂直速度随经度的分布Fig.2 The numerical simulation with basic flow U = 2 m/s: (a) The horizontal wind speed uversus longitude, the time interval is 2 d and the vertical level is at 9.8 km above equator; (b) the vertical wind speedversus longitude, the time interval is 2 d and the boundary layer top is at 1.03 km above equator

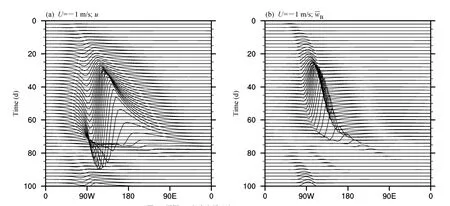
图3 同图2，但为水平风速U=－1 m/sFig.3 Same as Fig.2, but with basic flow U =－1 m/s

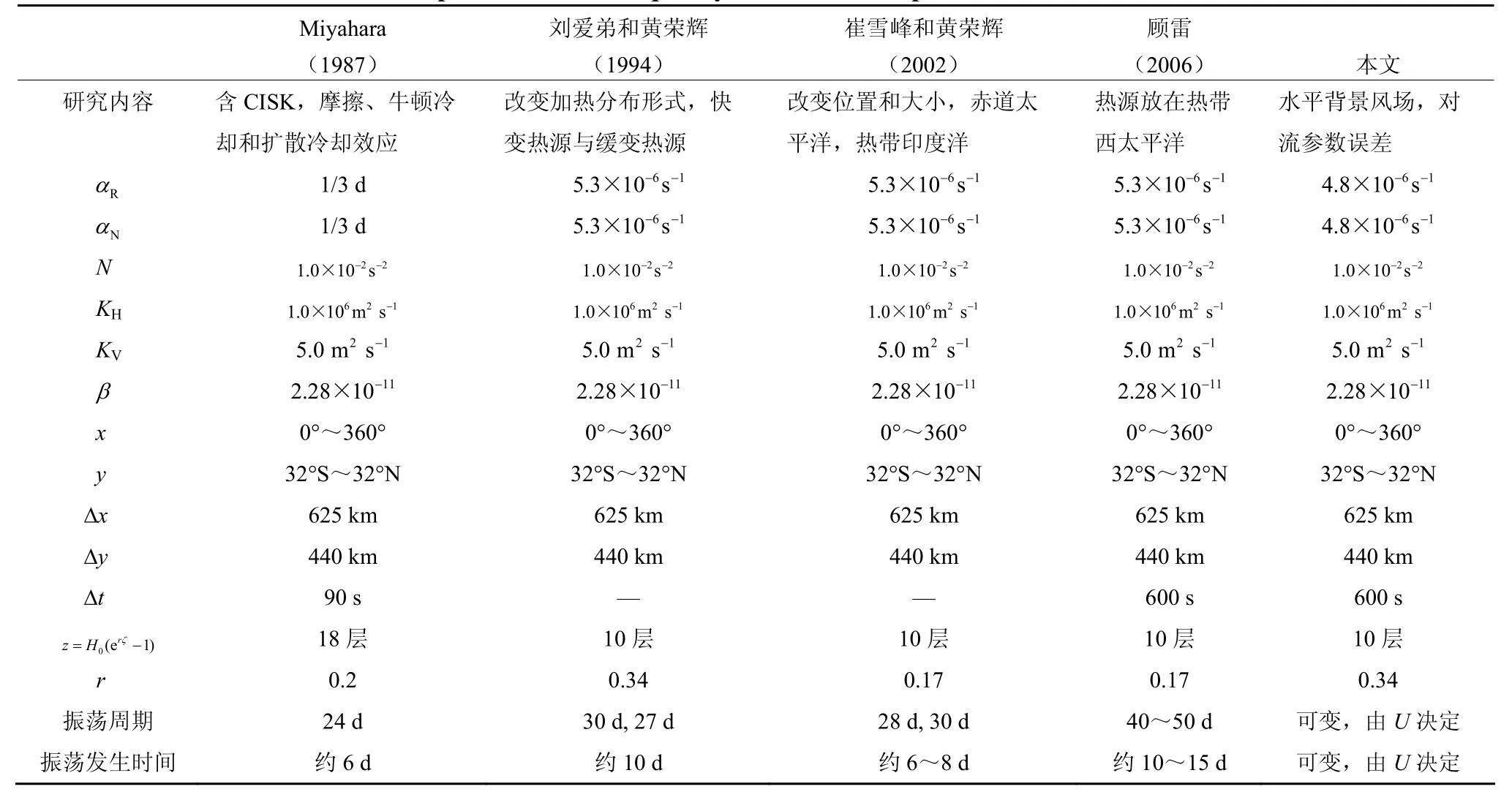
表2 一些研究中计算所用参数和得到的低频振荡周期Table 2 The periods of low-frequency oscillation and parameters in some studies

4 边界层顶参数化误差的影响

模式的参数化主要针对 η 和J，在整个模式中，除了加热项JH(x,y)和反馈项ηH(x,y)(x,y)外都是线性的，因此(x,y)的选择就很重要。模式中w的计算位于两层的中间，w层的数值见表 1，(x,y)是边界层顶（1030 m）垂直速度进行平滑得到的平均值，计算公式为：

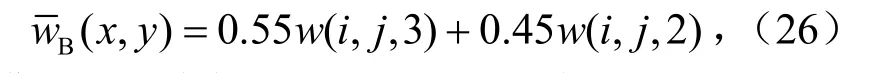
即是模式w层中第二层（665 m）和第三层（1340 m）垂直速度的线性拟合，对不同的分层，比例系数有不同。ηH(x,y)(x,y)这项的在计算时一般来说减小η和减小值的选取可取的相同的效果，但是的水平分布和η有差别，而且它们的变化在数值上有差别，一般先选取再确定η。

1）当边界层顶的选取出现误差时，例如(x,y)位于 1070 m，此时计算公式变为：(x,y) =0.60w(i,j, 3) +0.40w(i,j,2)，其它各项参数保持不变，得到的模拟结果如图4。图4中的风场在计算10 d后传播到80°～90°E 附近，此后扰动增长过快，扰动是不继续传播，而是出现了持续增长、数值解发散的现象，边界层顶的速度也是这样的变化趋势。

2）当边界层顶的选取为(x,y)位于1000 m时，计算公式变为：(x,y) =0.50w(i,j, 3) +0.50w(i,j,2)，其它各项参数保持不变，得到的模拟结果如图5。图5中的风场与图1相比扰动的振幅过小，扰动传播消失得很快，新的扰动又很快的发生，但振幅仍较小，如此循环。同样，边界层顶的速度也是具有振幅小，消失快的特点。

综合上述试验，如果选取过大，就会出 现扰动增长过快的现象，传播到 80°～90°E附近后，扰动不继续传播，而是无限增长。反之，选取过小时扰动增长太小，且衰减加快，扰动传播不远便耗散到零。

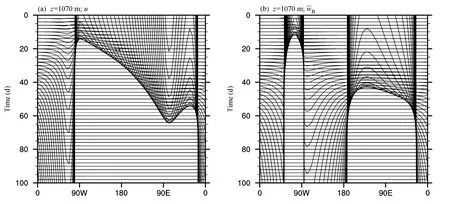
图4 同图1，但边界层顶取为z =1070 mFig.4 Same as Fig.1, but for boundary layer top z =1070 m

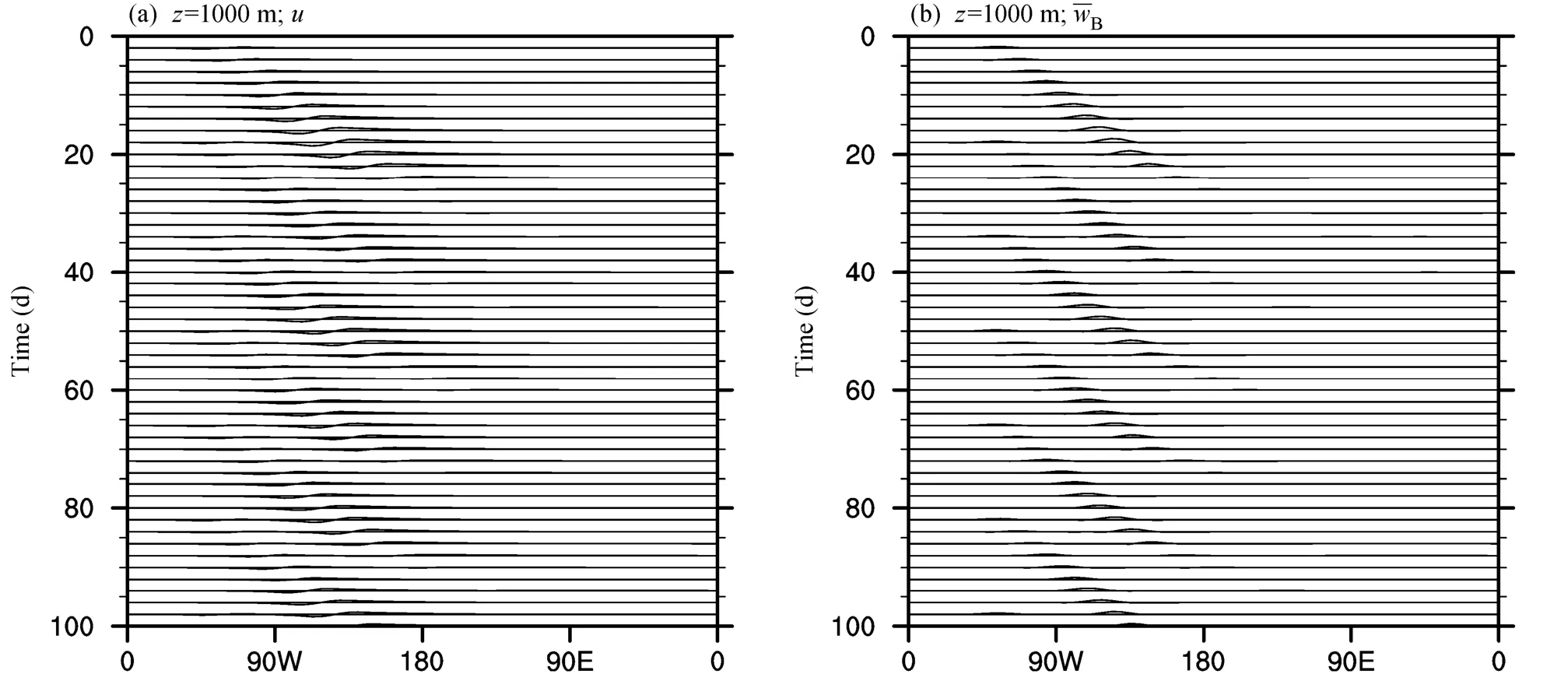
图5 同图1，但边界层顶取为z =1000 mFig.5 Same as Fig.1, but for boundary layer top z =1000 m

5 结论和讨论

本文以Miyahara所引入的CISK机制的热带简单大气扰动数值模式为基础，并加入了基本气流研究了边界层顶参数化误差对热带低频振荡模拟结果的影响。

当模式的边界层顶选取出现误差时，模拟结果会出现变化，研究发现ηH(x,y(x,y)的选取对低频振荡的模拟很重要，当边界层顶取得比标准值高时，出现扰动增长过快的现象，传播到 80°～90°E附近后，扰动不继续传播，而是无限增长。当边界层顶取得比标准值低时，扰动增长太小，且衰减加快，扰动传播不远便耗散到零。

此外，研究了在扰动方程中，基本气流对低频振荡数值模拟的影响。结果显示，当背景场为均匀U风场时，振荡周期和振荡发生时间随U的增加而减小，当U=2 m/s时，周期从 50～60 d减小到30 d；当U减小到U=－1 m/s时，振荡周期增加为70～80 d。由于低频振荡有从西向东传的趋势，因此当加入西风气流时，扰动向东传的速度加快是可以理解的，反之东风气流会抑制扰动东传的速度，使振荡周期增加。

波动CISK受到的水平基本气流影响应该包括纬向气流和经向气流两个方向，以往的研究中讨论纬向基本气流的较多，本文也是对纬向气流进行的讨论，但经向基本气流的作用可能也有很大的影响，例如李艳杰和李建平（2012）对球坐标下经向气流对行星波传播的影响进行了研究，发现经向基流使得定常波可以穿越东风带，在南北两半球间传播，为东西风带之间的相互作用提供了理论解释。因此，在波动CISK模式中考虑经向基本气流的作用，是需要在今后做进一步研究的。

（References）

巢纪平.2009.热带大气和海洋动力学 [M].北京: 气象出版社, 433pp.Chao J P.2009.The Dynamics of Tropical Atmosphere and Ocean (in Chinese) [M].Beijing: China Meteorological Press, 433pp.

Chang C P.1977.Viscous internal gravity waves and low-frequency oscillations in the tropics [J].J.Atmos.Sci., 34: 901–910.

崔雪峰, 黄荣辉.2002.热带强对流区域的位置和水平尺度对大气低频振荡的影响 [J].中国科学院研究生院学报, 19 (1): 49–58.Cui X F,Huang R H.2002.Impact of position and horizontal-scale of strong convection area on the low-frequency oscillation in the tropical atmosphere [J].Journal of the Graduate School of the Chinese Academy of Sciences (in Chinese), 19 (1): 49–58.

顾雷.2006.东亚夏季风爆发和推进过程的年际变化及其与春季热带西太平洋热力状态的关系 [D].中国科学院大气物理研究所博士论文.Gu L.2006.The interannual variation of eastern Asian summer monsoon onset and the relationship with the thermal state of tropical western Pacific Ocean [D].Ph.D.dissertation (in Chinese), Institute of Atmospheric Physics, Chinese Academy of Sciences.

Hayashi Y.1970.A theory of large-scale equatorial waves generated by condensation heat and accelerating the zonal wind [J].J.Meteor.Soc.Japan, 48: 140–160.

Huang R H.1994.Interactions between the 30-60 day oscillation, the Walker circulation and the convective activities in the tropical western Pacific and their relations to the interannual oscillation [J].Adv.Atmos.Sci., 11: 367–384.

Lau K M, Chan P H.1985.Aspects of the 40–50 day oscillation during the northern winter as inferred from outgoing longwave radiation [J].Mon.Wea.Rev., 113: 1889–1909.

Lau K M, Peng L.1987.Origin of low-frequency (intraseasonal)oscillations in the tropical atmosphere.Part I: Basic theory [J].J.Atmos.Sci., 44: 950–972.

李崇银.1985.南亚夏季风槽脊和热带气旋的活动与移动性CISK波 [J].中国科学（B 辑）: 15 (7): 668–675.Li C Y.1985.Actions of summer monsoon troughs (ridges) and tropical cyclones over South Asia and the moving CISK mode [J].Science in China (Ser.B) (in Chinese), 15 (7):668–675.

李艳杰, 李建平.2012.水平非均匀基流中行星波的传播 [J].地球物理学报, 55 (2): 361–371.Li Y J, Li J P.2012.Propagation of planetary waves in the horizontal non-uniform basic flow [J].Chinese Journal of Geophysics (in Chinese), 55 (2): 361–371.

Lindzen R S.1974.Wave-CISK in the tropics [J].J.Atmos.Sci., 31:156–179.

刘爱弟, 黄荣辉.1994.关于热带大气低频振荡的一个简单模式与数值模拟 [J].大气科学, 18 (3): 263–273.Liu A D, Huang R H.1994.A simple model and numerical simulation of low-frequency oscillation in the tropical atmosphere [J].Chinese Journal of Atmospheric Sciences (in Chinese), 18 (3): 263–273.

Madden R A, Julian P R.1971.Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific [J].J.Atmos.Sci., 28: 702–708.

Miyahara S.1987.A simple model of the tropical intraseasonal oscillation[J].J.Meteor.Soc.Japan, 65: 341–351.

沈新勇, 赵南, 何金海, 等.2006.切变基流对赤道大气波动稳定性的作用 [J].南京气象学院学报, 29 (4): 462–469.Shen X Y, Zhao N, He J H, et al.2006.Effects of shear flow on the stability of equatorial atmospheric waves [J].Journal of Nanjing Institute of Meteorology (in Chinese), 29 (4): 462–469.

Takahashi M.1987.A theory of the slow phase speed of the intraseasonal oscillation using the wave-CISK [J].J.Met.Soc.Japan, 65: 43–49.

赵强, 刘式适.2001.基本流场切变对赤道长Rossby波的影响 [J].气象学报, 59 (1): 23–30.Zhao Q, Liu S K.2001.Influence of the sheared basic flows on long equatorial Rossby waves [J].Acta Meteorologica Sinica (in Chinese), 59 (1): 23–30.