内蒙古呼和浩特市承压地下水水位监测网优化

屈泽伟, 张翼龙, 王贵玲*, 余 楚, 何雨江

1)中国地质大学(武汉)环境学院, 湖北武汉 430074;

2)中国地质科学院水文地质环境地质研究所, 河北石家庄 050800

内蒙古呼和浩特市承压地下水水位监测网优化

屈泽伟1), 张翼龙2), 王贵玲2)*, 余 楚2), 何雨江2)

1)中国地质大学(武汉)环境学院, 湖北武汉 430074;

2)中国地质科学院水文地质环境地质研究所, 河北石家庄 050800

定量评价地下水监测网的合理性对于准确、经济地获取高质量的监测数据尤为重要。本文针对呼和浩特市平原区现行承压水监测网, 以估计误差标准差作为衡量监测网合理与否的特征参数, 借助 ArcGIS地学统计模块, 利用普通Kriging插值模型, 对待测点进行插值, 获取估计误差标准差等值线图。结果表明: 监测水位估计误差标准差范围由优化前的0.47～4.44变为优化后的0.5～0.8(除研究区西南边界附近外), 研究区整体估计误差标准差显著减小, 且全区范围内变幅较小。优化后的监测网在满足监测精度需要的同时, 能够较大程度节省监测网的运行费用。研究成果为呼和浩特市平原区承压水水位监测提供一个较优化的监测网布设方案, 进而为研究区承压地下水的合理开发利用以及相关环境地质问题提供真实可靠的数据支撑, 具有重要的应用价值。

承压水; 地下水监测网; Kriging插值模型; 估计误差标准差

地下水动态监测是从地下水系统中提取信息的有效方法, 这些信息能正确地反映地下水系统中水位、水量等要素的时、空分布, 为地下水的合理开发利用和科学管理提供依据。随着地下水不合理的开发利用, 引发的环境问题日趋突出, 提高地下水监测网监测能力和监测质量已成为一种必然要求,这使得地下水监测网在地质环境工作中变得愈发重要(张翼龙等, 2012; 杨奉光, 2006; 周仰效等,2007)。

然而, 目前我国所运行的地下水监测网存在许多不足: 监测井点几何位置、分布密度的确定缺乏足够的科学依据; 监测井网不能满足地下水动态的监测要求; 监测数据丰富但有效信息匮乏等。如何能经济、合理、准确地获取满足一定条件的地下水动态资料成为目前亟待解决的问题(陈家军等, 1998;董殿伟等, 2007; 蒋庆, 2008; 邱元峰等, 2002; 郭占荣等, 1998; 陈植华, 2001; 梁国玲等, 2007)。

上述问题在呼和浩特市现行承压水监测网运作过程中反映突出。为更科学、经济地布设监测井网, 获取信息含量高的监测数据, 本文利用普通Kriging插值法对研究区承压水水位监测网进行优化配置。

1 研究区地下水水位监测网的现状

呼和浩特市自20世纪 60年代初以来, 就开始在城市水源地附近建立地下水监测网, 积累了大量的地下水动态监测资料。目前, 研究区范围内共有承压水水位监测井40眼(张翼龙, 2012)。

目前研究区现有监测网存在的主要问题如下:

(1)监测井空间布局的随意性和监测井数量不合理性

监测井布设位置随机性强, 主要表现在监测井密集于西北部的城区, 而在偏离城区的东部、南部区域缺少甚至没有监测井, 这就造成了局部信息冗杂而整体有效信息匮乏的尴尬局面。

(2)监测网不能应对特殊水文地质边界的变化

受人类活动大量开采承压地下水的影响, 研究区承压水天然流场已被分解成两个局部地下水流动系统, 仅依靠目前的监测网无法掌握区域上地下水流系统变化的情况, 同时也无法掌控淤泥层边界、无压区边界以及城区局部降落漏斗边界的变化情况。

针对以上问题, 为获得包含更多有效信息的监测数据, 必须对现有监测网进行优化。

2 Kriging插值模型

2.1 原理

Kriging法是建立在地质统计学基础上的一种方法, 区域化变量和半方差是Kriging插值法的基础,它是一种对时、空分布变量求最优、线性、无偏内插估计的方法(陶月赞等, 2003; Matheron, 1973)。根据已知监测井的数据, 对其进行结构性分析后, 利用待测点周围监测井的已知数据和被赋予的权系数,进行加权平均来获得待测点的数值(何雨江等,2010)。

Kriging模型:

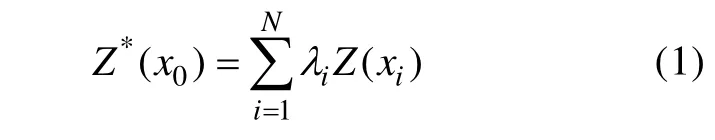
式中:Z*(x0)为区域化变量在x0点处的估计值;λi为Kriging权系数。

利用式(1), 在保证无偏性和最优性的前提下,结合协方差定义, 并引入拉格朗日算法, 可得:

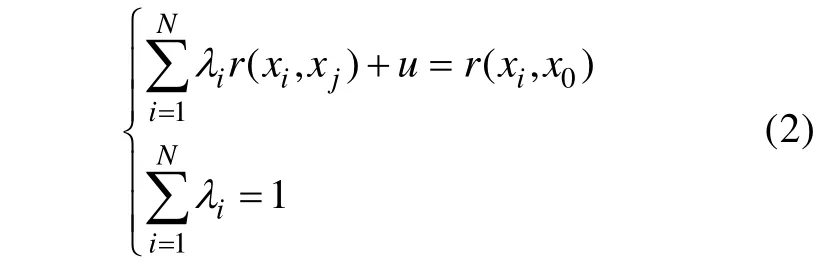
式中:r(xi,xj)为变差函数;u为拉格朗日算子。

利用式(2)并注意方差函数、协方差函数、变差函数在本征条件下的转换关系, 可得计算误差的理论方差为:

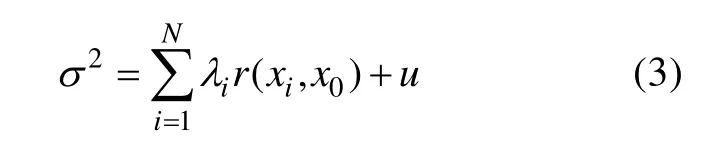
根据实际需要给定方差临界值σ02, 用现有监测井算出各处理论上的σ2, 当σ2<σ02时, 表示井网密度偏大, 需减少井点。当σ2>σ02时, 表示井网密度偏小, 需增加井点。

2.2 变差函数

变差函数既能描述区域化变量的空间结构性,又能描述随机性, 它是地质统计学计算的基本工具。理论上变差函数的表达式:

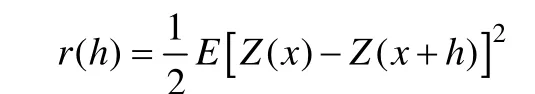
其中r(h)是两个变量的交互半方差值(周在明等, 2011)。

当监测点间距为h的数据对有M个时, 由xi及xi+h点的实测值计算变差函数为:

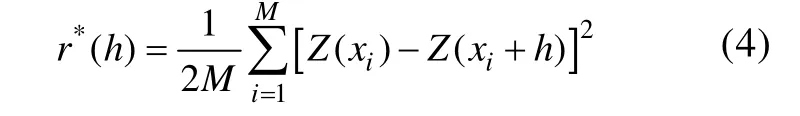
利用式(4)计算不同h对应的r*(h), 再根据最佳曲线拟合原理进行曲线拟合得到r*(h)关于h的最佳拟合曲线。常见的变差函数模型有: 球状模型、高斯模型、指数模型。在计算变差函数的过程中要与具体的地质条件相结合(矫希国, 1997)。

2.3 阶数N的确定

在采用 Kriging法对某点地下水位进行估计时,理论上整个研究区内地下水位均需要参与计算。但实际上, 某一点地下水位只与相近区域的地下水位值有关, 距离越远相关关系越小, 若所有点的地下水位值均参与计算容易产生病态, 为了避免这种现象的发生, 研究中常采用“内圈层”的 2到 5个监测点进行计算(刘治政等, 2010; 杨超, 2010)。

2.4 理论估计误差标准差的确定

在分析地下水监测网密度时, 对于临界方差值的选取, 目前我国尚无相应规范规定, 在实际应用中, 一般认为当监测点的误差理论方差在0.5～0.6之间时, 即理论估计误差标准差在0.7～0.8之间, 地下水监测网的密度能够满足实际需要且监测网的运行费用降到最低(杨超, 2010)。

3 呼和浩特市承压地下水监测网优化

3.1 研究区概况

研究区位于呼和浩特市大黑河冲湖积平原淤泥层界限内, 属于双层结构含水层系统即分为上部浅层地下水和下部深层承压水, 地势由北东向南西逐渐倾斜, 区内的主要河流为大黑河、小黑河。

研究区内深层承压含水层主要为第四纪中更新统下段( Q1)含水层, 其分布面积为 1084 km2, 上覆中更新统上段( Q2)湖积相淤泥质层, 其分布稳定、

2连续, 埋藏深度由东北部的20～25 m增加至西南部的40 m左右。连续、巨厚、稳定的淤泥质隔水层为承压水水质仍能基本保持天然的优质状态, 起到了极其重要的保护作用。含水层介质以湖滨相粗碎屑物为主, 含水层颗粒粗, 厚度大, 单井出水量大, 为具有区域供水意义的含水层, 是呼和浩特市城区主要地下水开采层。由于北部山前单层结构含水层系统地下水位大幅下降, 低于隔水层顶板的顶界, 浅水含水层在北部呈“无压”状态, “无压”区面积约 21 km2(见图 3)。

研究区内深层承压含水层系统主要补给源为东部、北部山前侧向径流, 其排泄主要为人工开采。地下水位动态主要受人工开采影响, 其次为山前潜水侧向径流补给的影响。

3.2 承压地下水监测网优化

3.2.1 变差函数的确定

根据研究区现有40眼承压井2010年的承压水水位统测资料(张翼龙, 2012), 利用 ArcGIS地学统计模块中Kriging插值模型, 通过选取不同模型以调参的方式对变差函数进行多次人工拟合后, 得到高斯模型拟合的效果最好(图1)。

为了保证拟合的效果, 进行了交互检验, 结果见表1。

从表 1可以看出: 由于标准平均值接近于零,说明不存在系统偏差, 平均标准误差和均方根接近,说明拟合的精度较好, 拟合各项指标如表2所示:

综上, 最终确定变差函数为:

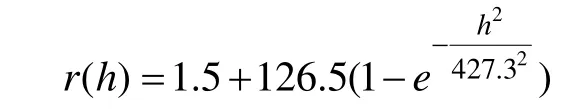
3.2.2 增(减)监测井前后估计误差计算

利用 ArcGIS软件地学统计模块, 通过 Kriging插值模型分别对研究区现有监测井网和重新布设后监测井网进行检验分析评价, 估计任一点估计误差的标准差, 进而得到估计误差标准差等值线图(图 2和图4)。由2

σ的表达式可以看出, 估计误差标准差仅与变差函数的类型和监测井点的位置有关, 而变差函数反应地下水系统的结构性特点, 对于特定的水文地质条件, 变差函数是一定的。那么估计误差标准差仅与监测井点的位置和数量有关, 并与监测井点分布密度呈反向关系, 即在监测井点密度大的地方, 其值偏小; 反之则偏大。这就为确定监测网最佳布设提供了理论依据。

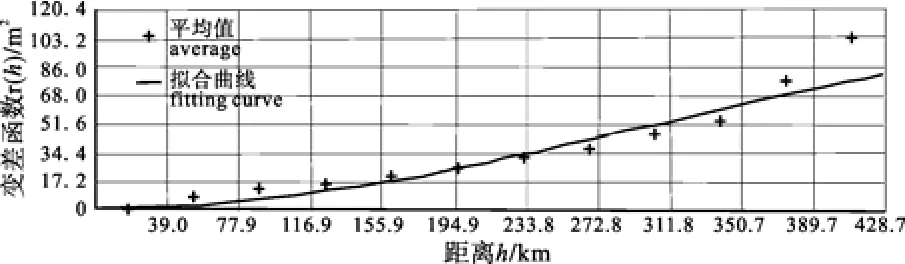
图1 变差函数拟合曲线图Fig. 1 Fitting curve of variation function

表1 交互检验结果Table 1 Results of cross validation

表2 研究区域变差函数参数表Table 2 Parameters of the variogram

由图2可以看出由呼和浩特市平原区现行承压地下水监测网监测地下水位估计误差标准差整体偏大, 而局部偏小, 计算结果在0.47～4.44之间。尤其是以城区为界限表现得更明显, 在西北部城区范围内估计误差标准差偏小, 而其它地区偏大, 这就说明研究区范围内监测井分布极为不均匀, 其分布密度在局部偏大, 而整体偏小。

区域优化目标: 优化后的监测网能在满足监测精度需要的同时, 较大程度上节省监测网的运行费用; 并能及时获取承压地下水水位动态监测数据,为呼和浩特市平原区承压地下水系统科学管理以及环境地质问题的防治提供科学依据。

为此, 在最大程度利用现有监测井的原则下,对研究区内监测井进行重新布设(图3), 保留现有监测井20眼, 在相应的位置增加监测井59眼, 共79眼, 布置原则:

①尽可能保证监测井在研究区内均匀分布;

②布设的监测井应尽量避开开采井, 以避免由于开采造成地下水水位波动的影响;

③于淤泥层边界处, 在现有监测井基础上增设新的监测井(Zc1、Zc10、Zc11、Zc17、Zc24、Zc30、Zc36、Zc37、Zc40、Zc43、Zc46、Zc39、Zc35、Zc29、Zc42、Zc43、Zc44、Zc45、Zc5、Zc2), 以共同监测淤泥层边界(即承压水边界)的迁移变化情况;

④于无压区边界处, 在现有监测井基础上增设新的监测井(Zc1、Zc2、Zc3、Zc4、Zc5、Zc6), 以监测无压区边界的变化情况;

⑤于城区地下水水位降落漏斗处, 按十字形布设 4条监测线(1-1、2-2、3-3、4-4), 并在现有监测井的基础上, 增设新的监测井(Zc8、Zc6、Zc1、Zc17),以共同监测降落漏斗的发展趋势;

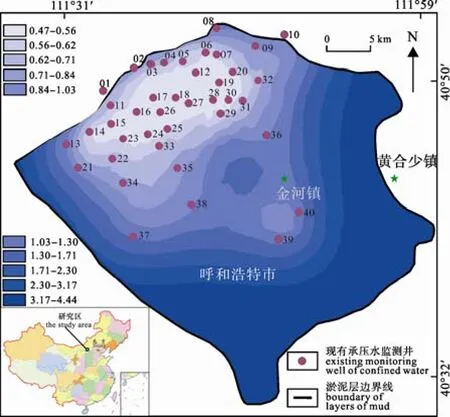
图2 优化前估计误差标准差等值线图Fig. 2 Contour diagram of the standard deviation of estimation error before optimization

⑥于地下水流动系统分水岭处东西向布设一条监测线(5-5), 并在现有监测井基础上于该监测线上或附近增设新监测井(Zc18、Zc19、Zc20、Zc21、Zc22、Zc23、Zc24、Zc25、Zc26、Zc27、Zc28、Zc42), 以共同监测承压地下水流场分水岭的迁移变化情况。

⑦在工作区东部、南部单一结构潜水区增设新的监测井(Zc47、Zc48、Zc49、Zc50、Zc51、Zc52、Zc53、Zc54、Zc55、Zc56、Zc57、Zc58、Zc59), 用以计算研究区内深层承压水从单一结构潜水区获得的地下水补给量, 从而在整体上把握工作区承压地下水流动系统的变化情况。

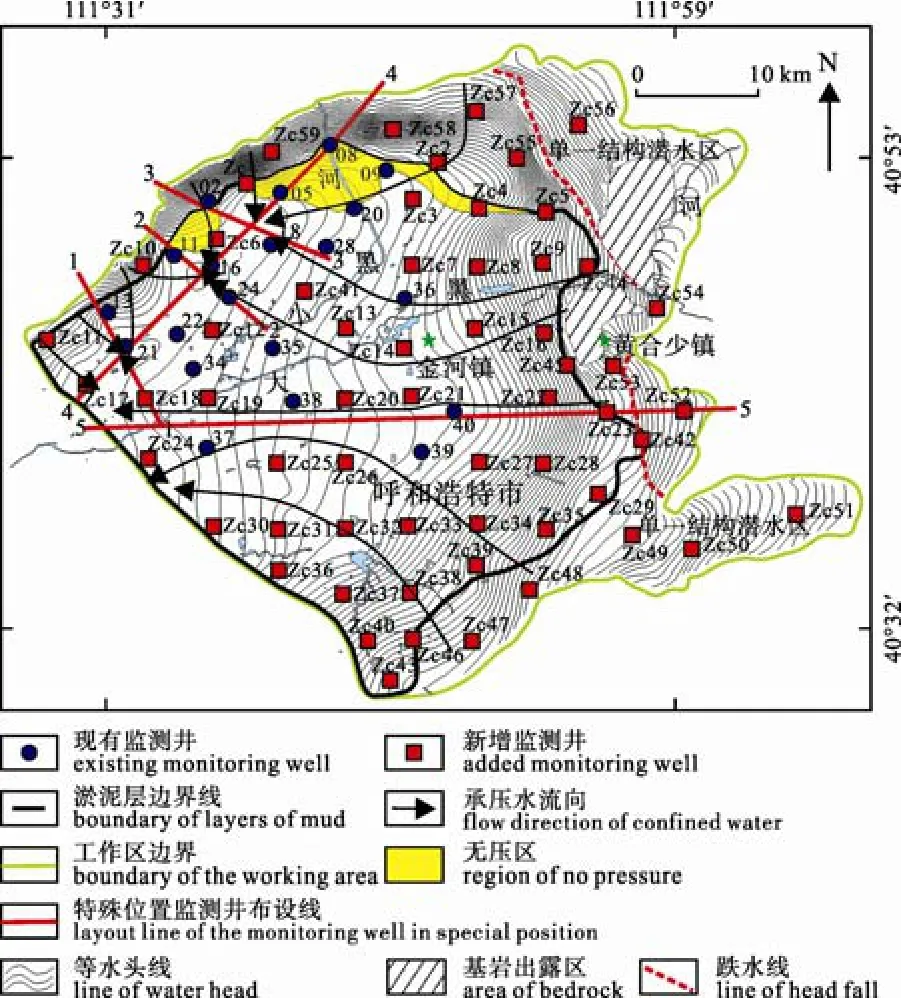
图3 优化后监测井分布图Fig. 3 The distribution of monitoring wells after optimization

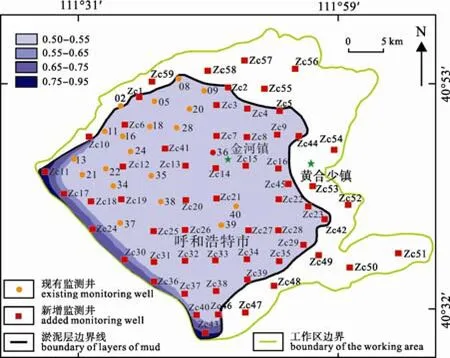
图4 优化后估计误差标准差等值线图Fig. 4 Contour diagram of the standard deviation of estimation error after optimization

由图4可见依据上述原则对呼和浩特市平原淤泥层边界内的监测井网进行重新优化布设后, 全区内估计误差标准差明显减少, 且在研究区大部分范围内估计误差标准差处于0.5～0.8之间, 能满足实际监测需要。

另外, 处于淤泥层内边界附近的监测井点处的估计误差标准差大于 0.8, 可能的原因是: 由于四方搜索法要求利用“内圈层”2～5个相关监测井, 而这些点处于研究区边缘, 在计算过程中会产生病态方程, 从而需要缩减 N数, 导致出现较大估计误差标准差, 这是不可避免的。

总体上, 对比优化前后的全区估计误差标准差,可以看出优化后的监测井网更为合理。

4 结论

本文借助ArcGIS地学统计模块, 在对呼和浩特市平原区现行承压地下水监测网进行定量评价的基础上, 根据区域优化目标和井位布置原则对其实施优化, 得到如下结论:

1)呼和浩特市平原区现行承压水水位监测网缺乏合理性, 估计误差标准差在监测井集中的地方小,能满足实际监测精度的需要, 但同时因监测网井点密度大, 加大了监测网运行成本。在监测井少甚至没有监测井的地方估计误差标准差相当大, 无法满足实际监测需要。

2)针对上述不足, 本文提出具体优化原则, 得到较为合理的承压水水位监测网优化方案: 保留现有监测井20眼, 在相应位置增设新监测井59眼, 共79眼监测井。优化后的监测网监测水位估计误差标准差较优化前显著减小, 且在全区内变化较小。其值范围在 0.5～0.8之间(研究区西南边界附近除外),能在较大程度上节省监测网运行成本, 并同时满足实际监测精度的需要。

陈家军, 王红旗, 张征, 王金生. 1998. 地质统计学方法在地下水水位估值中应用[J]. 水文地质工程地质, (6): 7-10.

陈植华. 2001. 地下水观测网的若干问题与基于信息熵的研究方法[J]. 地学前缘, 8(1): 135-142.

董殿伟, 林沛, 晏婴, 刘久荣, 叶超, 郑跃军, 万利勤, 李文鹏,周仰效. 2007. 北京平原地下水水位监测网优化[J]. 水文地质工程地质, 34(1): 10-19.

郭占荣, 刘志明, 朱延华. 1998. 克立格法在地下水观测网优化设计中的应用[J]. 地球学报, 19(4): 429-433.

何雨江, 靳孟贵, 刘延锋, 汪丙国. 2010. 南疆棉田表层土壤盐分的空间变异特征分析与应用[J]. 地质科技情报, 29(6):90-92.

蒋庆. 2008. 地下水时空变化及监测网多目标优化研究[D]. 武汉:华中科技大学.

矫希国. 1997. 变差函数参数的计算[J]. 地质论评, 43(6):659-663.

刘治政, 吴晓东, 林洪孝. 2010. Kriging插值模型在地下水位监测网优化中的应用[J]. 人民长江, 41(9): 14-17.

梁国玲, 张永波, 张礼中, 周小元, 张春英. 2007. 基于GIS的中国地下水资源空间数据库建设[J]. 地球学报, 28(6):572-578.

邱元峰, 罗金耀, 孟戈. 2002. 地下水观测井网优化设计[J]. 水文地质工程地质, (6): 38-41.

陶月赞, 郑恒强, 汪学福. 2003. 用Kriging方法评价地下水监测网密度[J]. 水文, 23(2): 46-48.

杨奉光. 2006. 乌鲁木齐河区域地下水监测网优化[D]. 乌鲁木齐:新疆大学.

杨超. 2010. 银川平原地下水水位监测网优化设计[D]. 西安: 长安大学.

张翼龙. 2012. 呼和浩特市(市区)地下水资源保护与开发利用调查评价项目成果报告[R]. 石家庄: 中国地质科学院水文地质环境地质研究所.

张翼龙, 陈宗宇, 曹文庚, 李政红, 王文中, 王丽娟, 于娟, 刘君.2012. DRASTIC与同位素方法在内蒙古呼和浩特市地下水防污性评价中的应用[J]. 地球学报, 33(5): 819-825.

周仰效, 李文鹏. 2007. 区域地下水位监测网优化设计方法[J].水文地质工程地质, (1): 1-9.

周在明, 张光辉, 王金哲, 严明疆. 2011. 环渤海低平原水土盐分与水位埋深的空间变异及协同克立格估值[J]. 地球学报,32(4): 493-499.

CHEN Jia-jun, WANG Hong-qi, ZHANG Zheng, WANG Jin-sheng.1998. Geostatistical approach to groundwater level estimation[J]. Hydrogeology & Engineering Geology, (6): 7-10(in Chinese with English abstract).

CHEN Zhi-hua. 2001. Some confusions in groundwater monitoring network and the entropy method[J]. Earth Science Frontiers,8(1): 135-142(in Chinese with English abstract).

DONG Dian-wei, LIN Pei, YAN Ying, LIU Jiu-rong, YE Chao,ZHENG Yue-jun, WAN Li-qin, LI Wen-peng, ZHOU Yang-xiao. 2007. Optimum design of groundwater level monitoring network of Beijing Plain[J]. Hydrogeology & Engineering Geology, 34(1): 10-19(in Chinese with English abstract).

GUO Zhan-rong, LIU Zhi-ming, ZHU Yan-hua. 1998. The Application of Kriging Estimation to the Optimal Design of Groundwater Observation Network[J]. Acta Geoscientica Sinica,19(4): 429-433(in Chinese with English abstract).

HE Yu-jiang, JIN Meng-gui, LIU Yan-feng, WANG Bing-guo. 2010.Spatial variability of soil salt on the surface of cotton fields in the south of Xinjiang[J]. Geological Science and Technology Information, 29(6): 90-92(in Chinese with English abstract).

JIANG Qing. 2008. Research on Spatio-temporal Changes of the Groundwater and Monitoring Network Muti-objective Optimization[D]. Wuhan: Huazhong University of Science and Technology(in Chinese with English abstract).

JIAO Xi-guo. 1997. A new method for calculating parameters of the variogram[J]. Geological Review, 43(6): 659-663(in Chinese with English abstract).

LIU Zhi-zheng, WU Xiao-dong, LIN Hong-xiao. 2010. Kriging interpolation model and its application in optimization of groundwater level monitoring network[J]. Yangtze River,41(9): 14-17(in Chinese with English abstract).

LIANG Guo-ling, ZHANG Yong-bo, ZHANG Li-zhong, ZHOU Xiao-yuan, ZHANG Chun-ying. 2007. The Construction of Spatial Database for Groundwater Resourcein China Based on GIS[J]. Acta Geoscientica Sinica, 28(6): 572-578(in Chinese with English abstract).

MATHERON G. 1973. The intrinsic random function and their applications[J]. Advances in Applied Probability, 5: 429-468.

QIU Yuan-feng, LUO Jin-yao, MENG Ge. 2002. Optimal design of the groundwater observation-wells network[J]. Hydrogeology& Engineering Geology, (6): 38-41(in Chinese with English abstract).

TAO Yue-zan, ZHENG Heng-qiang, WANG Xue-fu. 2003. Assessment for Density of Groundwater Network using Kriging[J]. Hydrology, 23(2): 46-48(in Chinese with English abstract).

YANG Feng-guang. 2006. Design of a groundwater level monitoring network for Urumqi river aera[D]. Urumqi: Xinjiang University(in Chinese with English abstract).

YANG Chao. 2010. Optimum design of groundwater level monitoring network of Yinchuan plain[D]. Xi’an: Chang’an University(in Chinese with English abstract).

ZHANG Yi-long. 2012. Report of Hohhot (urban area), groundwater resource protection and development and utilization of the investigation and evaluation[R]. Shijiazhuang: Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Sciences(in Chinese).

ZHANG Yi-long, CHEN Zong-yu, CAO Wen-geng, LI Zheng-hong,WANG Wen-zhong, WANG Li-juan, YU Juan, LIU Jun. 2012.The Application of DRASTIC and Isotope Method to the Evaluation of Groundwater Vulnerability in Hohhot, Inner Mongolia[J]. Acta Geoscientica Sinica, 33(5): 819-825(in Chinese with English abstract).

ZHOU Yang-xiao, LI Wen-peng. 2007. Design of regional groundwater level monitoring networks[J]. Hydrogeology & Engineering Geology, (1): 1-9(in Chinese with English abstract).

ZHOU Zai-ming, ZHANG Guang-hui, WANG Jin-zhe, YAN Ming-jiang. 2011. Spatial Variability of Soil Salinity, Total Dissolved Solid and Groundwater Depth Based on Cokriging in the Low Plain around the Bohai Sea[J]. Acta Geoscientica Sinica, 32(4): 493-499(in Chinese with English abstract).

The Optimization of Monitoring Networks for Confined Water in Hohhot, Inner Mongolia

QU Ze-wei1), ZHANG Yi-long2), WANG Gui-ling2)*, YU Chu2), HE Yu-jiang2)
1)School of Environmental Studies, China University of Geosciences(Wuhan), Wuhan, Hubei430074;
2)Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Sciences,Shijiazhuang, Hebei050800

The quantitative evaluation of the rationality of the groundwater monitoring network is particularly important for the precise acquisition of high quality monitoring data. In this paper, the existing monitoring networks for confined water in Hohhot plain area was chosen as the research target and the standard deviation of estimation error was adopted as the parameter for evaluating the rationality of the monitoring networks. With the aid of ArcGIS geological statistical module, the interpolation was performed on the study points by dint of Kriging interpolation model to acquire the contour line of the standard deviation of the estimation error. The results show that the standard deviation of the estimation error of the monitoring water level changed from 0.47～4.44 (before optimization) to 0.5～0.8 (after optimization, except for the area near the southwest boundary of the study area).The overall standard deviation of the estimation error significantly decreased. The optimized monitoring network can satisfy the monitoring accuracy and, at the same time, the operation cost of the monitoring network can be reduced to a large extent. The research results can preliminarily provide a better optimizing monitoring well layout scheme for the confined water-level monitoring of the Hohhot plain, and can provide reliable scientific

data for future research on the rational development and utilization of confined water and the related environmental-geological problems, which will be of high practical importance.

confined water; groundwater monitoring network; Kriging interpolation model; standard deviation of estimation error

P641.132; O241.3

A

10.3975/cagsb.2013.02.09

本文由国家973项目“华北平原地下水演变机制与调控”(编号: 2010CB428802)和中国地质调查局地质大调查项目“全国地下水资源及其环境问题调查评价”子项目“河套平原地下水资源及其环境问题调查评价”(编号: 1212010913010)联合资助。

2012-08-26; 改回日期: 2012-11-12。责任编辑: 张改侠。

屈泽伟, 男, 1986年生。硕士研究生。主要从事地下水科学与环境方面的研究。E-mail: qzw_cug@126.com。

*通讯作者: 王贵玲, 男, 1964年生。研究员, 博士生导师。主要从事水资源与地热研究。E-mail: guilingw@163.com。