基于熵权模糊物元的武广客专引入长沙铁路枢纽方案

王顺利，王正彬

(西南交通大学峨眉校区 交通运输系，四川 峨眉 614202)*

0 引言

客运专线引入铁路枢纽站址方案的比选，有些指标可以定量衡量，而有些指标只能通过人们的主观判断，它们的共同点是不确定性和模糊性.模糊综合评价是以模糊数学为基础，应用模糊关系合成原理，将一些边界不清，不易定量的因素定量化，进行综合评价的一种方法［1］.在模糊综合评价法中，各指标的权重不好确定，传统的方法往往依靠专家的经验来判断，掺杂了大量主观因素，从而导致最后的评判结果可能与实际相背离［2］.

熵权法根据各评价指标数值的变异程度所反映的信息量大小来确定权重，将主观判断与客观计算相结合，避免了权重的主观性，增加了权重的可信度［3］.本文在模糊物元分析的基础上结合熵理论，建立基于熵权的模糊物元评价模型，有效避免了评价标准的不确定性，对方案进行有效且全面的比选.

1 熵权模糊元模型

1.1 模糊物元评价集

任何事物(R)可以用“事物(M)、特征(C)、量值(x)”三个要素加以描述，若三要素中的量值(x)具有模糊性，则称R为模糊物元.某事物R有m个事物(M)，事物(M)有n个特征C1、C2，…，Cn及相应的量值x1，x2，…，xn，则构成m个事物n维复合模糊物元Rmn:

1.2 从优隶属度

在方案的评价指标体系中，由于各评价指标采用的量纲不同，不能直接通过评价指标值进行方案的综合评价和排序，故需要先对各评价指标的量值进行统一处理，对评价指标进行规范.各项评价指标相应的模糊量，从属于标准方案各对应评价指标相应的模糊量值隶属程度，称为从优隶属度［4-5］.各备选方案的评价指标并不是越大越好，评价指标分为成本性指标和收益性指标，成本性指标越小越好，收益性指标越大越好，根据评价指标的不同对Rmn进行标准化处理.

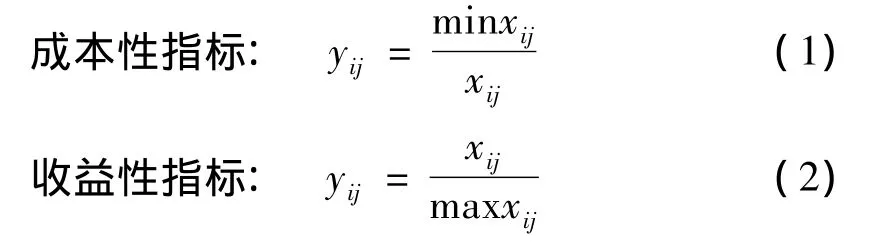
1.3 差平方模糊物元

在各评价指标中，最优的量值处理后为1，则用其他量值减去1后取平方，则构成了模糊物元的差平方矩阵R△mn.

计算评价指标的熵

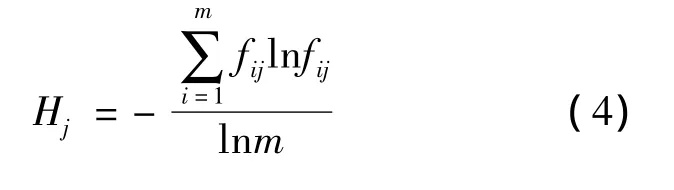
且

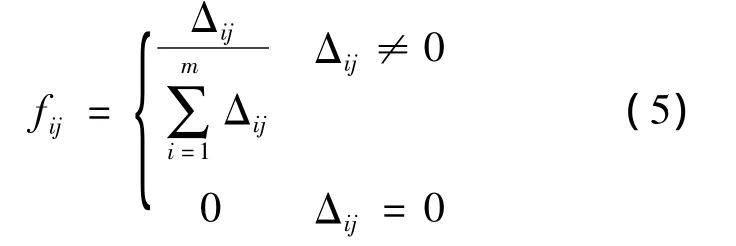
计算评价指标的权重

且

计算贴近度并对方案排序

贴近度是指评价样本与标准样本两者相互接近的程度，其值越大表示两者越接近，反之则相离较远，可以根据贴近度的大小对各方案进行优劣排序.可用于物元贴近度有欧氏贴近度、海明贴近度、测度贴近度等多种，考虑到具体评价意义，本文计算各评价方案的欧氏贴近度，并按照欧氏贴近度的大小对各方案进行排序，从而确定最优的评价方案.

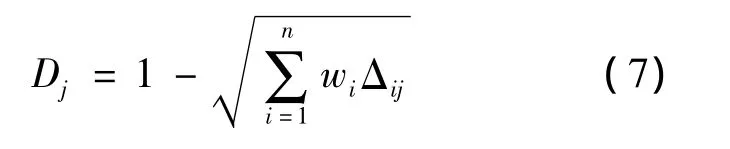
2 选址方案比选

武广客运专线引入长沙枢纽的客运站选址，经过现场勘查和实际比对，可得到3个备选站址方案，即引入既有长沙站方案(方案I)、长沙东站地址方案(方案II)、长沙南站址方案(方案II)［6］.

2.1 评价指标体系建立

对3个备选方案，遵循科学性和可操作性相结合、系统性与层次性相结合，重要性与全面性相结合，本文对武广客专引入长沙枢纽构建了工程投资、发展余地、拆迁量、与城市规划相配合等11个评价指标，并对各评价指标赋值，如附表所示.

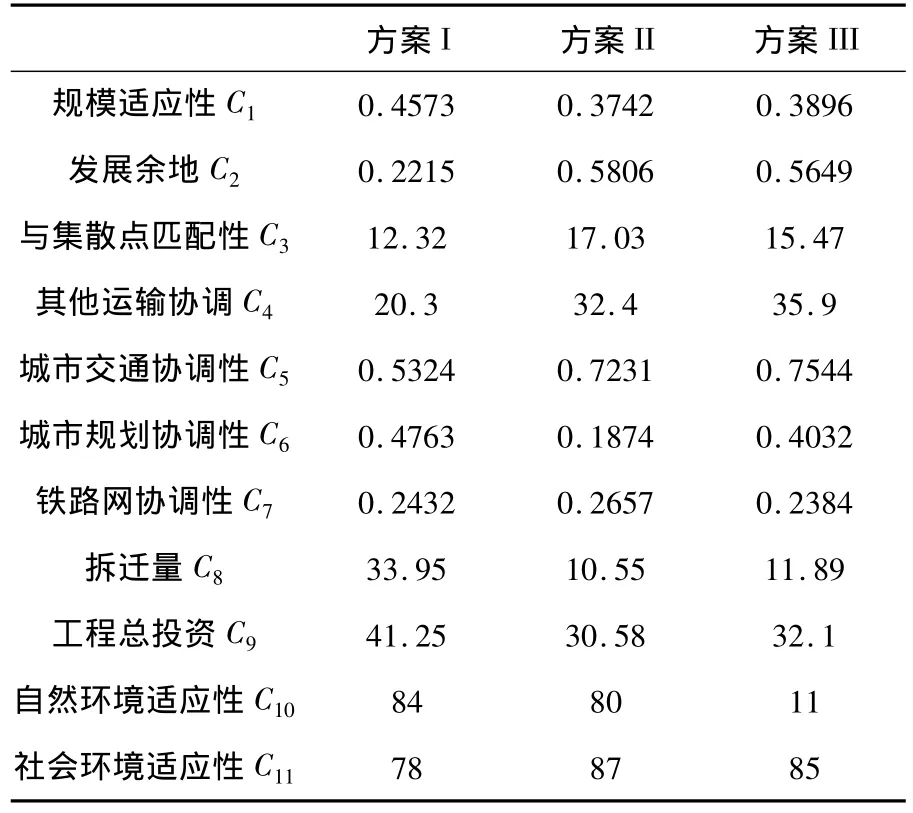
附表 3个备选方案的评价指标值

2.2 根据从优隶属度构建标准模糊元矩阵

在11个评价指标体系中，规模适应性C1、与集散点匹配性C3、其他运输协调C4、城市交通协调性C5、城市规划协调性C6、拆迁量C8、工程总投资C9越小越优;发展余地C2、铁路网协调性C7、自然环境适应性C10、社会环境适应性C11越小越优.根据式(6)、(7)建立标准模糊元矩阵.

根据R，构建差平方矩阵R△，如下所示:

2.3 确定评级指标权重系数并确定最优方案

根据公式(4)、(5)、(6)计算评价指标的熵Hj、熵权 wj.

根据式(7)可分别计算出三个方案的欧氏贴近度，对三个方案按欧氏贴近度进行排序:方案Ⅰ、Ⅱ、Ⅲ的欧氏贴近度分别为0.622、0.875、0.812;排序分别为 3、1、2.

由结果可知，方案Ⅱ为最优方案.

3 结论

熵权模糊元分析法应用于客运专线引入铁路枢纽客运站选址，应用熵权法计算评价指标的权重，减少了人为因素对评价结果的干扰，最后通过计算欧氏贴近度来实现评价方案的排序，选出最优方案.

［1］曾蓉，陈洪凯.熵权模糊综合评价法在公路洪灾危险性评价中的应用［J］.重庆交通大学学报(自然科学版)，2010，29(4):587-591.

［2］李琼.客运专线引入枢纽方案及站址问题研究［D］.成都:西南交通大学，2010.

［3］潘巧玲，焦永兰.基于集对分析的客运专线引入铁路枢纽客运站站选址方案比选［J］.中国铁道科学，2009(5):125-129.

［4］何磷，广晓平.基于熵权模糊元分析的客运专线引入铁路枢纽的客运站选址方案研究［J］.兰州交通大学学报，2010(8):126-129.

［5］罗君君，郑俊杰，孙玲.公路软基处理方案优选的熵权模糊元决策法［J］.铁道科学与工程学报，2008，5(4):20-24.

［6］张鑫，蔡焕杰.基于熵权模糊元模型在节水灌溉项目评价中的应用［J］.节水灌溉，2009(1):5-8.