基于Adams积分的GLONASS卫星位置解算
2013-09-19饶才杰白志强
吕 达,饶才杰,刘 岩,白志强
(中国航天科工信息技术研究院,北京100070)
0 引言
组合GPS/GLONASS增加了观测卫星的个数,提高了卫星的可用性,改善了卫星定位的几何结构,通过融合可以提高定位精度和可用性,解决GPS网络RTK定位中困难地区的定位问题,具有重要应用价值[1,2]。因此,研究 GLONASS 系统定位尤其是组合定位有重要实用价值。如何根据GLONASS广播星历进行卫星位置计算是组合定位的重要一环。GLONASS广播导航电文没有给出开普勒轨道参数,对于一个给定的时刻,不能通过最新的导航电文参考时刻的开普勒轨道参数直接计算卫星位置。GLONASS导航电文给出的是PZ-90坐标系下参考时刻卫星的运动状态向量,包括参考时刻卫星的位置、速度和日月摄动加速度等,每30 min更新一次,这决定了对于某一时刻的卫星位置,需要以上述的卫星运动状态向量为初值,采用受力模型通过积分得到[3]。
大量的国外文献对GPS卫星位置的计算方法进行了阐述,但对GLONASS卫星位置计算方法的研究较少。目前GLONASS卫星轨道数值积分方法主要有龙格—库塔法(Runge-Kutta),其中以四阶龙格—库塔法最为常用(简称R-K法)。文献[4]等推导了GLONASS卫星在地固坐标系中的运动方程,并简要介绍了利用龙格—库塔法进行轨道积分的数值结果;文献[5]对龙格—库塔法进行了分析;文献[6]利用龙格—库塔法实现了GLONASS卫星轨道求解;文献[7]完成了定步长龙格—库塔法的计算程序。但是,龙格—库塔法在计算某一时刻卫星位置和速度时只用到前一步的信息,为了保证定位精度,需要多次重新计算多个点处的函数值[8],计算量较大。这里采用基于Adams预测校正公式的GLONASS卫星轨道积分法来实现GLONASS卫星位置解算,该方法通过较多地利用前面几步的已知信息,在保证较高精度的前提下,运算量降低为龙格—库塔法的50%,同时稳定性更好。实验结果表明,新方法是一种求解GLONASS卫星位置的有效方法。
1 卫星的运动方程
GLONASS卫星在 PZ-90坐标系下的运动方程为[3]:

式中,x,y,z分别表示卫星在PZ-90坐标系下的坐标;vx,vy,vz分别表示3个方向的卫星速度;地球引力常量μ=398 600.44 km3/s2;卫星到地球质心的距离r=;地球的长半轴ae=6 378.136 km;地球重力位第二带谐系数=0.001 082 63;地球自转速度 ω =0.000 072 921 15 rad/s;为日月摄动加速度。t时刻式(1)的函数形式可以表示为:
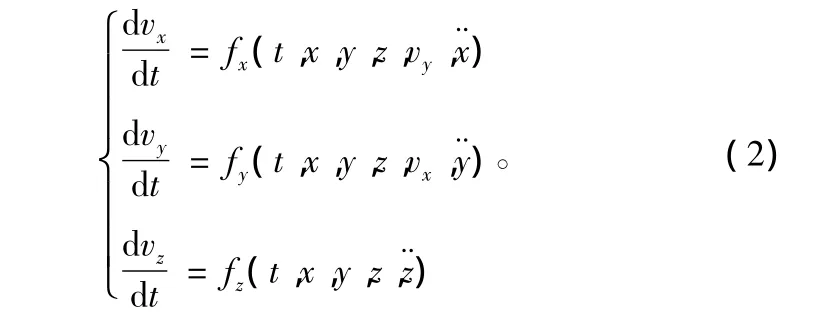
2 Adams卫星位置计算方法
GLONASS卫星运动方程在 x,y,z三方向的分式均可以抽象成如下微分方程:

其等价的积分方程为:

采用插值多项式代P(t)替上式右端的被积函数,从而使其离散化以得到数值公式:

则 Adams显式公式为[8]:

Adams隐式公式为[8]:
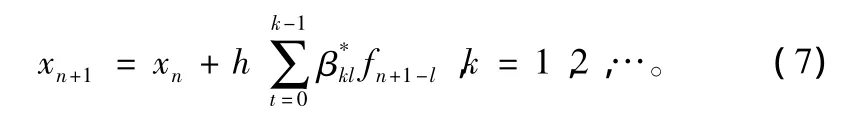
本文研究应用 Adams线性多步法来进行GLONASS卫星位置解算,通过较多地利用前面几步的已知信息,来构造计算量小、精度高的GLONASS卫星位置解算的新算法。Adams性多步公式包括隐式方法和显式方法,同阶的隐式公式比显式公式精确,而且稳定性也好。这里将四步四阶显示公式作为预测公式,将三步四阶隐式公式作为校正公式联合使用,如式(8)所示:

截断误差分别为:

用局部截断误差进一步修正预测值和校正值,可以得到更精确的预测—校正公式:

将GLONASS卫星的加速度值代入式(8)进行积分,就得到了GLONASS卫星的速度,对速度值进一步积分,就可以得到GLONASS卫星的位置坐标。采用修正后的预测校正公式(10)可以进一步减小截断误差。
3 Adams积分法与龙格—库塔法比较
Adams算法的计算量大约是R-K方法的50%。采用四阶龙格—库塔法进行一步积分运算公式如下:
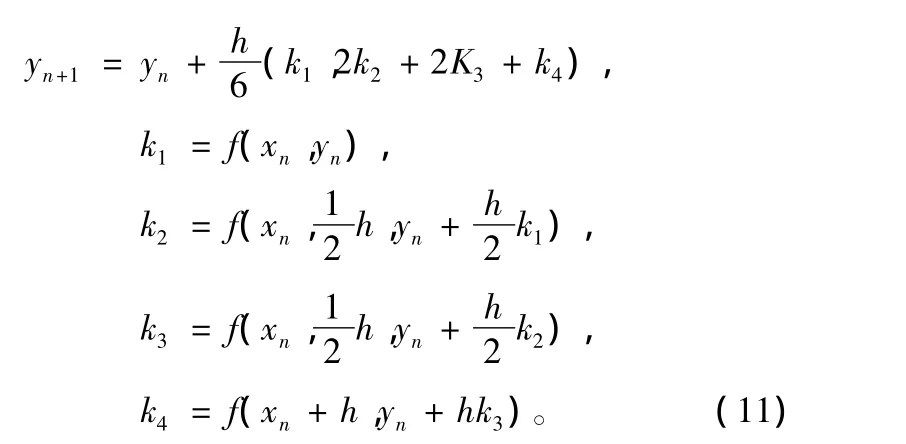
使用龙格—库塔法由yn计算yn+1时,只用到前一步的信息yn,为了提高运算精度,需要重新计算4次函数值f(x)。采用Adams由yn计算yn+1时,用到前4 步的信息 yn-3、yn-2、yn-1和 yn,只需分别计算1次函数值f(x)、f(x+1),运算量相当于计算2次函数值f(x)。由于计算函数值f(x)(即加速度)是GLONASS轨道积分过程中运算量较大的部分,所以Adams算法运算量大约是龙格—库塔法的50%。
使用Adams预测校正公式可以达到龙格—库塔法相同的精度,使用修正Adams预测校正公式的精度可以比R-K方法高一阶,使预测校正公式的截断误差达到o(h6)。
4 实验结果及分析
选取2009年8月29日23:45至2009年8月31日16:45每间隔半小时共82个时刻,GLONASS 2号卫星的广播星历作为实验数据。
分别使用Adams方法与R-K方法,以2009年8月29日23:45至2009年8月31日15:45每半小时间隔的参考时间向前轨道积分30 min,得到2009年8月30日00:15至2009年8月31日16:15半小时间隔的共81个时刻的,GLONASS 2号卫星位置的X、Y、Z坐标,再将计算结果与广播星历里给出的卫星坐标进行比较,得到二者差值的统计结果如表1所示。
分别使用Adams方法与R-K方法,以2009年8月29日23:45至2009年8月31日15:15每半小时间隔的参考时间向前轨道积分60 min,得到2009年8月30日00:45至2009年8月31日16:15半小时间隔的共80个时刻的GLONASS 2号卫星位置的X、Y、Z坐标,再将计算结果与广播星历里给出的卫星坐标进行比较,得到二者差值的统计结果如表2所示。

表1 30 min轨道积分结果 (单位:m)
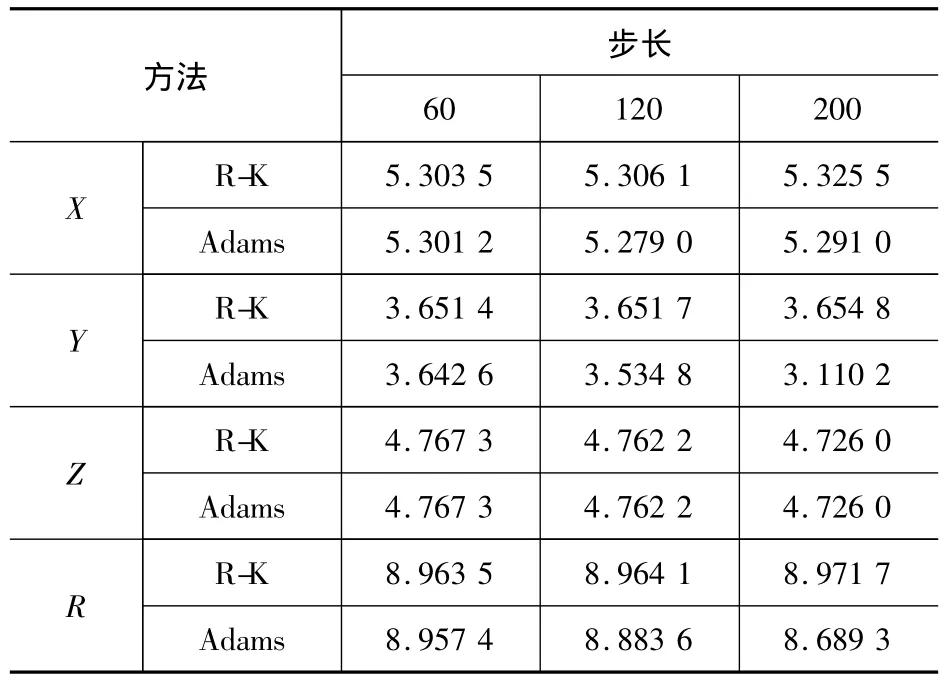
表2 60 min轨道积分结果 (单位:m)
对试验数据分析如下:
①向前积分30 min,选取不同步长对2种算法的误差影响不大,2种算法误差都比较小,但Adams算法比R-K算法误差的均值要小。向前积分60 min,Adams算法优势更加明显,如以200为步长积分时,R-K算法距离误差均值为 8.971 7,而Adams法为 8.689 3。
②随着积分时间延长,2种算法的误差随之增大,但Adams算法的均值误差小于R-K算法,且随着积分时间越长越明显,说明Adams算法稳定性[8]优于R-K算法。
③采用R-K方法进行一步积分,需要计算4次三维方向的加速度;采用Adams进行一次运算,只需要计算2次;由于轨道积分运算的代价主要取决于计算加速度的次数,所以Adams算法的运算量约为R-K算法的50%。
5 结束语
采用了Adams预测校正公式进行GLONASS卫星位置解算,并采用GLONASS的广播星历对新算法和R-K算法的积分结果和运算效率进行分析,证明了所提方法是一种有效的GLONASS卫星位置解算方法。与四阶R-K算法相比,新算法精度高、稳定性好,而且运算量降低了50%。采用基于Adams预测校正公式的GLONASS卫星轨道积分法进行GLONASS位置解算,对确保多系统兼容GNSS接收机的精度、实时性等方面有重要意义。
[1]Bruyninx Carine.Comparing GPS – only with GPS+GLONASS Positioning in a Regional Permanent GNSS Network[J].GPS Solutions,2007,11(2):97-106.
[2]Alexei E Zinoviev.Using GLONASS in Combined GNSS Receivers:Current Status[C]∥ION GNSS 18th International Technical Meeting of the Satellite Division.Long Beach,CA,USA,2005:1 046-1 057.
[3]ICD-GLONASS.GLONASSInterface Control Document Version 5.1,ICD 2008E[M].Moscow:Coordination Scientific Information Center,2008.
[4]葛茂荣,过静珺,葛胜杰.GLONASS卫星坐标的计算方法[J].测绘通报,1999(2):2-4.
[5]杨 剑,王泽民,孟 泱,等.GLONASS卫星轨道积分算法分析[J].武汉大学学报:信息科学版,2006,31(7):613-615.
[6]李建文.GLONASS卫星导航系统及GPS/GLONASS组合应用研究[D].郑州:信息工程大学,2001:25-29.
[7]葛 奎,王解先.GLONASS卫星位置计算与程序实现[J].测绘与空间地理信息,2009,32(2):137-140.
[8]丁丽娟,程杞元.数值计算方法[M].北京理工大学出版社,2008:241-246.
