基于能量法的高速叶轮热耗散研究

高 兴, 黄 科, 段 浩



基于能量法的高速叶轮热耗散研究

高 兴, 黄 科, 段 浩

(中国船舶重工集团公司第705研究所昆明分部, 云南昆明, 650118)

涡轮机叶轮的高速转动过程是能量耗散过程, 温度变化是研究塑性变形能量耗散的重要参量。本文对真空试验台中的高速叶轮进行研究, 通过建立的模型用解析方法分析其应变能与热能耗散的联系。得出了弹性应变能和塑性应变能分别对叶轮热耗散过程的影响。从试验中观察得到的温度变化现象验证了计算结果的有效性, 为系统分析叶轮在实际工况中的热耗散作用提供了理论依据和支持。

涡轮机叶轮; 能量法; 热耗散; 应变能

0 引言

1870年, Tresca第1次用文字详细记录了塑性变形过程中产生的热能。后来的许多学者在研究后发现, 塑性变形过程是一个从稳定状态, 经历不稳定平衡态失稳, 再到新的稳定态的过程。因此, 这样耗散结构中的能量耗散是伴随着材料塑性变形损伤过程中的非平衡不可逆变化而必然产生的, 在宏观上则表现为热耗散。热耗散的多少能够反应材料不同的破坏过程中的差异, 同时也能够体现材料变形损伤过程中的不可逆性。而叶轮在高速转动过程中, 其转动过程也是一个能量耗散的过程。能量耗散形式主要包括内耗热和储能两部分。

材料形变过程中的内耗热是由内摩擦引起的, 即一部分晶粒相对于另一部分的晶内剪切移动、摩擦而产生热。国内外学者对研究变形过程中的热现象都展开了系统研究。Hopkinson和Williams在试验中发现热耗散能量与静态过程迟滞能存在差异[3] 。Clarebrough 等通过各种试验证实了在此过程中储能的存在。Wong等将有限差分法和最小二乘原理结合起来计算热耗散, 并将其用于非稳态的问题[5] 。Harry研究了钢在扭转状态下的热响应, 发现热耗散量是应力幅的函数[6] 。姚磊江等通过用热敏电阻对高强度钢、铝合金和钛合金这3种材料疲劳过程的能量耗散与热发射进行分析, 研究了在此过程中的热发射规律。Taylor和Farren测量了材料塑性变形过程中的热产生, 发现热耗散率与塑性功率的比值约为0.9。Golos和Ellyin用包括塑性应变能和弹性应变能的总应变能作为损伤参量进行能量耗散研究[7] 。

本文旨在通过对叶轮在高速试验台中塑性变形中热能耗散的研究, 初步探讨叶轮损伤变形过程中的生热机理, 同时对由内耗热作用引起的叶轮温度场的变化进行理论计算, 通过与测量所得的试验数据进行对照, 研究工程金属在高速转动过程中的温度变化现象。

1 叶轮变形过程中的能量描述

叶轮在转动过程中, 在材料的应力应变曲线的不同阶段, 能量的累积及热耗散的规律是不一样的。在开始屈服阶段, 显微结构的变化比较剧烈, 产生大量不可逆的畸变组织, 能量较多地存储于晶格缺陷中。进入稳定阶段后, 显微结构趋于稳定变化, 并且随着变形过程的深入, 部分畸变组织有可能在变形过程中湮灭, 以热量的形式释放出自由能, 当达到一种饱和状态, 即新生的畸变组织与消失的畸变组织数量相等, 全部变形能转化成热能。但由于微裂纹的存在, 完全饱和状态很难完全达到, 在实际中温度还是会存在持续呈现微小上升。总而言之, 在材料的塑性变形过程中, 材料的温度升高和材料的变形能是正相关的。在叶轮的转动过程中, 当旋转角速度达到发生塑性变形的临界点以后, 随着转速的提高, 塑性变形在整个叶轮盘面呈不断上升的趋势, 材料的变形能和内能也会随之增大, 温度也相应地呈持续上升的过程。消耗于塑性变形的能量绝大部分转化成了热, 另一部分与晶格缺陷有关的能量以形变累积能即储能的形式残留在形变金属中, 从而引起材料物理性能的改变。

关于在金属塑性变形中热耗散与形变积累能之间的关系, 众多学者都通过理论计算或者试验研究认定, 在塑性变形过程中约有90%左右的能量转化为材料的内耗热, 而另外10%的能量以储能的形式造成了金属的裂纹和损伤。在本文用到的超速试验模型中, 可以清晰地看到叶轮由于变形能的破坏而产生的鱼鳞状变形损伤。

能量储存有多种机制, 包括点阵畸变(弹性应变能)和点阵缺陷。其中点阵缺陷占绝大部分。材料的点阵缺陷主要包括位错、空位、形变晶界等。由于点阵缺陷的形成和分布非常复杂, 并且各种缺陷之间还存在复杂的相互作用, 因此从微观角度去研究材料的能量状态是不现实的。但是由于能量守恒原理, 可以从宏观角度对叶轮塑性变形中的热耗散进行研究。Koh等用总应变能密度代替塑性应变能密度。总应变能密度包括塑性应变能密度和与拉应力相关的弹性应变能密度, 并得到以下的能量关系

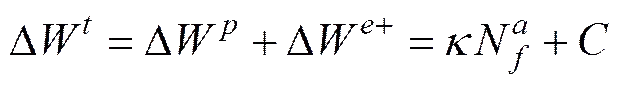
从宏观上讲, 材料塑性变形过程的能量耗散可以表示为以下的能量平衡方程

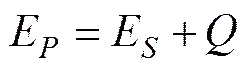
根据Wong以及Taylor和Farren等学者的研究认为, 约有90%的塑性变形能转化为了叶轮的热能; 另外10%的储能造成了金属的裂纹和损伤。在本文的计算中, 由于叶轮的转动在真空试验台中进行, 整个系统与外界无能量交换, 所以在度量系统热能的时候可以测量叶轮自身的温度而得到。

这样, 构建出另一个能量方程

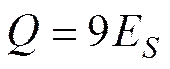
在本文所考虑的叶轮计算模型中, 叶轮(如图3所示)在真空试验台中的转速为5233rad/s, 在此转速下, 叶轮产生了塑性变形区和弹性变形区(如图4所示)。

图3 试验中的叶轮模型

Fig. 3 Impeller model for experiment

根据叶轮的不同变形区域, 把叶轮分为以下塑性变形区和弹性变形区, 可以把总的变形能细分为塑性变形区内的弹性应变能、塑性应变能以及弹性区内的弹性应变能, 分别进行分析计算。

Table 69 理论分析

在研究叶轮在高转速下能量耗散问题时, 要用到叶轮的自身参数(如表1所示)和已经得到的叶轮变形的解析解或近似解。由于叶轮所用钛合金的热膨胀系数极小, 在测量叶轮转动过程中的结构变化和体积变化时可以忽略热膨胀变形的影响, 近似地认为热耗散只对由弹/塑性变形引起的热力学内变量有关。这样就可以直接利用能量法中应力应变与变形能之间的关系对叶轮的变形能及内能进行解析计算。

表1 叶轮主要参数

由于计算弹性应力应变和塑性应变需要采用不同的计算公式, 故分开计算叶轮的应变能, 从而求得叶轮的内能。通过应力应变曲线(如图5所示)中对不同单元段的应力应变进行积分可以求得各自的变形能。

其中弹性应变能由两部分组成, 一是叶片塑性变形区内低于屈服极限而具有弹性应变, 利用图5中左图所示应力应变曲线, 这一部分的能量用以下解析方法即可求得

(6)

则

···

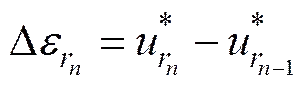
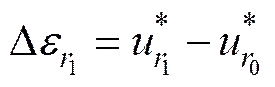
(8)

如图5中图所示, 从而可以得到弹性区内的弹性变形能

(10)

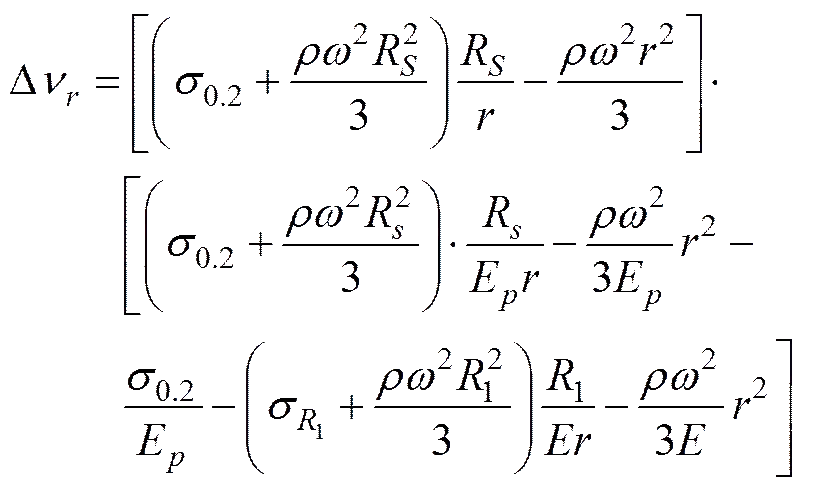
叶轮盘面半径从到R的区域对进行积分, 得到整个叶轮在转动过程中的塑性变形能的大小

(12)

3 实例计算

经过对叶轮变形能的理论分析, 得到如下3个计算弹性应变能和塑性应变能的公式。

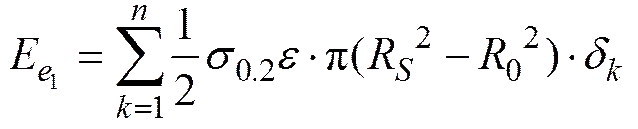
(14)

(15)

经简化, 略去高阶小量, 计算后得到

(17)

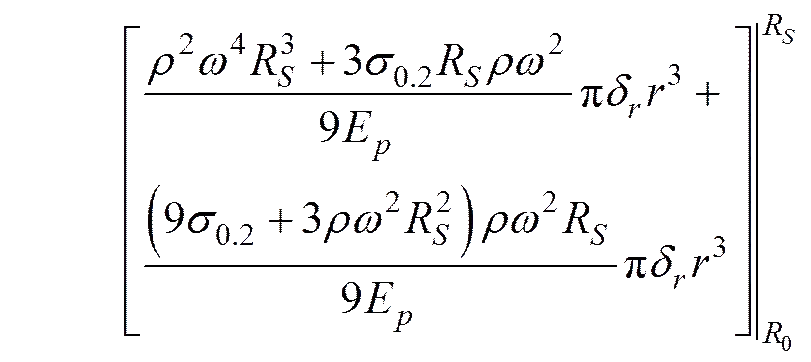
根据热耗散与应变能之间的关系

(19)

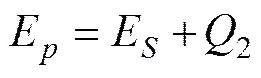
(21)

Liaw P K和Yang B等提出当没有外部热源的作用时, 金属在弹/塑性变形过程中的温度变化受热弹性效应、塑性响应和热传导3个方面的影响。Luong M P, La Rosa G和Risitano A等从试验中发现, 在塑性功占主导地位的情况下, 若加载频率一定, 当载荷对应的应力水平低于材料相应的疲劳耐久极限时, 材料表现的宏观温度变化不太明显; 当高于时, 其温度变化可以分为3个特征明显的阶段, 如图6所示。

图中: 第1阶段为初始升温阶段, 此阶段大部分热量耗散用于提高材料温度, 温度上升较快, 直至稳定, 进而可求得叶轮温度升高; 第2阶段为温度稳定阶段, 这一阶段的温度耗散主要用于和周围环境进行热交换。但由于超速试验在真空试验台中进行, 与周围环境没有热交换, 所以几乎没有温度稳定的阶段; 第3阶段为材料损伤发生时的快速升温阶段, 这一阶段中金属裂纹进入拓展阶段, 由于裂尖的能量快速释放, 导致材料表明温度在很短时间内快速上升。

不考虑第2阶段的对流和热传递影响, 得到在真空试验台中的叶轮温度变化曲线见图7。

由于在真空试验台中叶轮温度变化的特殊性, 在应用能量法进行求解系统温度升高的能量控制方程中, 可以忽略对流换热量等项的影响, 直接应用固体材料的热传导效应相关的各向同性材料在绝热条件下的热能公式

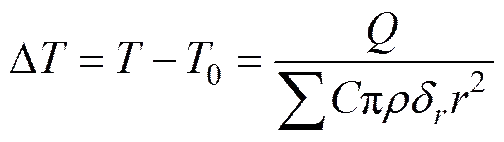
4 试验验证

在真空试验台上对涡轮机叶轮进行超速试验如图8所示, 当转速为5 233 rad/s时, 得到叶轮的径向变形量随着半径的增大而逐渐加大, 并且随着转速不断提高, 温度变化十分显著。所得叶轮超速试验结果见表2所示。

表2 叶轮超速试验结果

5 结论

1) 通过计算可以看出, 由弹性应变能引起的点阵畸变在总储能中所占的比例很小, 约占3%左右。因此, 储能大部分是由于点阵缺陷引起的。叶轮生热主要与塑性变形等非弹性行为有关。这部分能量是构成叶轮破坏损伤的根源所在。在与外界无热交换的条件下, 由材料晶体结构间内摩擦引起的热耗散与材料塑性应变能存在严格正相关。在材料裂纹拓展阶段, 残余变形量的大小可以通过对温度的测量而近似得到。

2) 文章利用能量法的原理在能量控制方程中计算得到叶轮的温度升高为, 与超速试验的实测结果相对照, 两者偏差小于2.3%。说明本文中基于能量法的叶轮温度计算模型能有效地为研究叶轮转动过程中的能量特性提供分析依据。

3) 在真空试验台中, 叶轮在高速转动中所具有变形能全部转化成内能, 本文用解析法得到的叶轮的温度变化值在实际工况中也可作为计算叶轮温度的依据。因温度场与应变场在材料仅发生弹性应变时并无直接联系, 一旦塑性变形引起材料显微结构变化, 材料在承受载荷吸收机械能的过程中, 可激发损伤区域造成大量的热产生。迅速产生的大量热能与周围的环境的热交换并不能在短时间内有明显体现, 故此方法可作为分析叶轮高速转动中产生热能和温度变化的理论基础。

[1] Bell J. The Experimental Foundations of Solid Mechanics [M]. New York: Springer-Verlag, 1973.

[2] 姚磊江, 童小燕, 吕胜利. 金属低周疲劳的能耗耗散与热发射[J]. 机械科学与技术, 2003, 22(5): 709-801.Yao Lei-jiang, Tong Xiao-yan, Lü Sheng-li. On Energy Dissipation and Thermal Emission of Metals Under Low Cycle Fatigue [J]. Mechanical Science and Technology, 2003, 22(5): 709-801.

[3] Hopkinson B, Williams G T. The Elastic Hysteresis of Steel[C]//Proceedingsof Royal Society, 1912: 10-17.

[4] Clarebrough L M, Hargreaves M E. Energy Stored During Torsional Oscillation[J]. Mechanics Physical Solid, 1962(10): 235-240.

[5] Wong A K, Kirby C. A Hybird Numerical/Experimental Technique for Determine the Heat Dissipated During Low Cycle Fatigue[J]. Engineering Fracture Mechanics, 1990, 37(3): 453-493.

[6] Harry R, Joubet F, Gomaa A. Measuring the Actual Endurance Limit of One Specimen Using a Non Destructive Method[J]. Journal of Engineering Material Technology, ASME, 1981, 103(1): 71-76.

[7] Golos K, Ellyin F. Total Strain Energy Density Theory as a Fatigue Damage Parameter. Advances in Fatigue Science and Technology[C]//Proceedings of NATO Advanced Study Institute, Alvor, Portugal, 1989: 849-853.

[8] 童小燕, 王德俊, 徐灏. 低周疲劳损伤过程的自热温升变化特征[J]. 金属学报, 1991, 27(2): 149-152.Tong Xiao-yan, Wang De-jun, Xu Hao. Infrared Detection of Self-heating Process During Low Cycle Fatigue Damage[J]. Acta Metallurgica Sinica, 1991, 27(2): 149-152.

[9] Koh S K. Fatigue Damage Evaluation of a High Pressure Tube Steel Using Cyclic Strain Energy Density[J]. Interna- tional Journal of Pressure Vessels and Piping, 2002, 79(12): 791-798.

[10] 童小燕, 王德俊, 徐灏. 疲劳损伤过程的热能耗散分析[J]. 金属学报, 1992, 28(4): 163-169.Tong Xiao-yan, Wang De-jun, Xu Hao. Heat Energy Dissi- pation in Fatigue Damage Process of Materials[J]. Acta Metallurgica Sinica, 1992, 28(4): 163-169.

[11] 冯明珲, 吕和祥, 郭宇峰. 粘弹塑性统一本构模型理论[J]. 计算力学学报, 2001, 18(4): 424-434.Feng Ming-hui, LÜ He-xiang , Guo Yu-feng. A Theory of the Visco-elastic-plastic Unifield Constitutive Model and the Comparison with Others[J]. Chinese Journal of Computa- tional Mechanics, 2001, 18 (4): 424-434.

[12] 丁晓玲, 刘建林, 刘刚. 从宏观和微观来看内能与应变能[J]. 沈阳工程学院学报(自然科学版), 2006, 2(1): 27-28. Ding Xiao-ling, Liu Jian-lin, Liu Gang. View on Internal Energy and Strain Energy Form Macroscopy and Micro- scopy[J]. Journal of Shenyang Institute of Engineering (Natural Science), 2006, 2(1): 27-28.

[13] 汤安民, 李智慧. 对弹性力学势能原理等价性提法的商榷[J]. 西安理工大学学报, 2012, 28(3): 326-329.Tang An-min, Li Zhi-hui. Discussions on the Equivalence of Potential Energy Principle in Elastic Mechanics[J]. Journal of Xi′an University of Technology, 2012, 28(3): 326-329.

[14] 甘露萍, 黄洪钟, 袁容, 等. 基于总应变能密度的轮盘低周疲劳寿命模型及可靠性研究[J]. 中国科技论文, 2012, 7(8): 616-621.Gan Lu-ping, Huang Hong-zhong, Yuan Rong, et al. Low Cyclic Fatigue Life Model and Reliability Analysis of Turbine Disks Using Total Strain Energy Density[J]. China Sciencepaper, 2012, 7(8): 616-621.

[15] 安虎平, 芮执元, 王锐锋, 等. 基于最小能量法的高速切削锯齿状切屑变形分析[J]. 工具技术, 2012, 46(10): 7-10.An Hu-ping, Rui Zhi-yuan, Wang Rui-feng, et al. Analysis for Deformation of Serrated Chips Formed during High Speed Machining Based on Minimum Energy Consumed[J]. Tool Engineering, 2012, 46(10): 7-10.

[16] 徐楠, 陈举华. 局部应力应变疲劳的能量方法[J]. 山东大学学报(工学版), 2006, 36(1): 15-18.Xu Nan, Chen Ju-hua. Energy Method of Local Stress and Strain Fatigue[J]. Journal of Shandong University(Enginee- ring Science), 2006, 36(1): 15-18.

[17] 刘浩, 赵军, 丁桦. 疲劳过程中生热机理的实验探讨[J]. 实验力学, 2008, 23(1): 1-8.Liu Hao, Zhao Jun, Ding Hua. Experimental Study on Heat Production Mechanism during Fatigue Process[J]. Journal of Experimental Mechanics, 2008, 23(1): 1-8.

[18] 童小燕, 姚磊江, 吕胜利. 疲劳能量方法研究回顾[J]. 机械强度, 2004, 26(S): 216-221.Tong Xiao-yan, Yao Lei-jiang, Lü Sheng-li. Review on Fatigue Energy Theory[J]. Journal of Mechanical Strength, 2004, 26(S): 216-221.

(责任编辑: 陈 曦)

Thermal Dissipation Analysis of High-speed Turbine Impeller Based on Energy Method

GAO Xing, HUANG Ke, DUAN Hao

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

Operation of high-speed turbine impeller dissipates energy. The variation of temperature is a key parameter for analyzing energy dissipation in its plastic deformation. This paper analyzes the relation between strain energy and heat dissipation of a high-speed turbine impeller on a vacuum test-bed via an established model by using analytical method, and obtains the effects of elastic strain energy and plastic strain energy on heat dissipation of the impeller. The temperature variation observed in experiment validates the computational result, which can provide theoretical reference to systemically analyze thermal dissipation in actual working conditions.

turbine impeller; energy method; heat dissipation; strain energy

TJ635;TH313

A

1673-1948(2013)03-0206-07

2013-03-05;

2013-05-28.

高 兴(1986-), 男, 在读硕士, 主要研究方向为水下发射技术.