爆炸破片对防护液舱的穿透效应*
2013-09-19孔祥韶吴卫国李晓彬徐双喜
孔祥韶,吴卫国,李 俊,李晓彬,徐双喜
(武汉理工大学交通学院,湖北 武汉 430063)
大型水面舰船舷侧均设有防护液舱,其主要作用是防御反舰武器对内部重要舱室的破坏。高速破片穿过液舱的过程可分为4个阶段[1],即穿透液舱外板、破片在液体中运动、形成气穴和穿透液舱内板。破片穿透过程中与舱内液体的作用机理非常复杂,近期的研究主要集中在破片在液体中运动时产生的冲击波、压力、气穴、破片速度衰减等特性,以及液舱舱壁的变形和破坏情况。M.Lee等[2]研究了高速物体入水产生的压力波的传播,建立了理论计算模型;D.Townsend等[3]通过系列实验,研究了液体容器在高速破片冲击下的破坏情况。D.Varas等[1]研究了不同液位的容器在高速破片打击下的响应,并采用LS-DYNA中的ALE和SPH方法模拟了实验过程,验证了数值计算方法的有效性和准确性[4]。此外,M.Nishida等[5]、P.J.Disimile等[6]、J.P.Brog等[7-9]、N.Lecysyn等[10-12]有针对性地开展了大量的实验、理论分析和数值计算。
目前的研究主要是针对单个破片穿透液体容器的过程。本文中对破片穿过液舱的过程进行数值计算,分析单发和双发破片的速度衰减规律、舱内液体的响应及液舱内外板的变形和破坏,重点讨论破片间距离对上述方面的影响,进一步探讨液舱对破片群的防御能力。在此基础上,对防护液舱的设计提出有参考价值的建议。
1 反舰导弹战斗部破片特性
当导弹战斗部在舰艇舱室内部爆炸时,战斗部壳体在爆轰产物作用下将发生膨胀、破裂,形成大量大小不等的高速破片。以某反舰导弹为对象,其战斗部技术参数为:全长,624.2mm;总质量,230kg;装药长度,484.2mm;装药直径,374.4mm;装药质量,89.1kg;装药种类,B炸药。
战斗部爆炸产生的破片平均速度可采用Gurney公式[13]计算得到,即:

破片质量的计算最常用的是Mott公式:
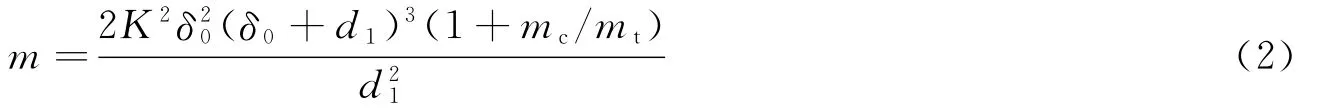
式中:mt为战斗部有效段壳体质量,kg;mc为装药质量,kg;m 为破片的平均质量,kg;δ0为弹壳壁厚,m;d1为弹壳内直径,m;K 为取决于炸药的系数,kg0.5·m-1.5,B类炸药的 K=8.91kg0.5·m-1.5。
将相关参数代入式(2),得战斗部爆炸产生的破片平均质量m=27.5g。
2 液舱对爆炸破片的防御作用
2.1 破片在液体中的运动规律
破片在无反射边界液体中运动时,描述破片的运动方程如下:

式中:m为破片的质量,v为破片的速度,ρl为液体的密度,A 为破片与液体的接触面积,Cx(t)为破片的阻力系数。
由式(3)可解得破片在液体中运动时不同时刻的速度可表示为:

式中:d为球形破片直径,ρ为破片材料密度,v1为破片穿透液舱外板后的速度。
2.2 液体中的冲击波
破片穿透液舱外板后与舱内液体发生相互作用,将破片的动能传递给部分液体,使舱内液体中产生冲击波。P.C.Chou等[14]给出了破片撞击液体产生的冲击波随时间的传播距离R(m)和冲击波速度us(m/s)的计算公式分别为:
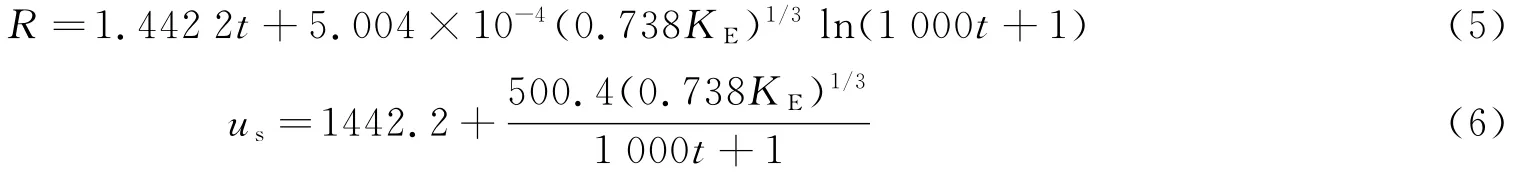
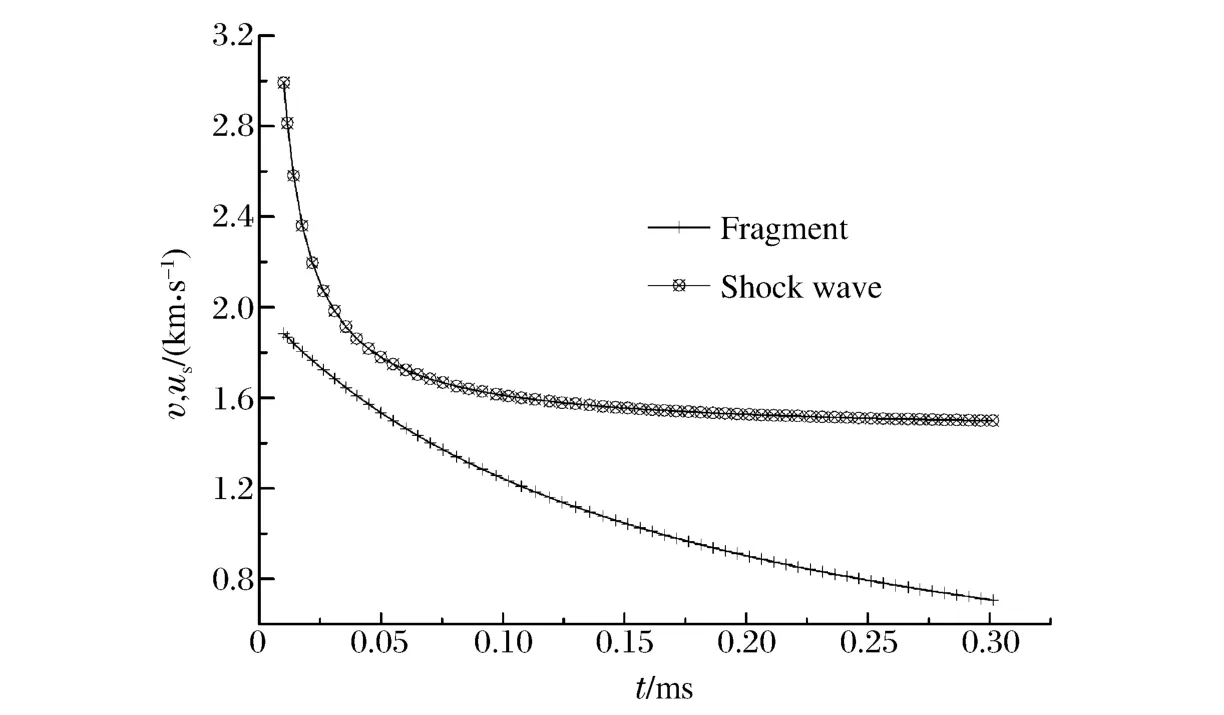
图1 液体中破片和冲击波的速度衰减曲线Fig.1 Velocity attenuation curves of fragment and shock wave
式中:KE为破片入水时的动能,J;t为破片在液舱中的运动时间,s。
根据式(4)和(6)可得到质量m=27.5g、初速度v0=2km/s的球形破片及破片在液体中形成的冲击波的速度衰减曲线,如图1所示。破片撞击液体时形成的冲击波初始速度很高,之后迅速衰减。在破片与液体接触后的0.05ms内,冲击波速度衰减比破片速度衰减更快,两者的速度差减小。但之后,随着破片的动能逐渐传递到液体中,其速度衰减更明显,冲击波速度衰减趋势逐渐变缓。
3 爆炸破片对液舱的穿透过程
3.1 数值计算方法验证
本文中采用AUTODYN中的SPH求解器对破片穿透液舱的过程进行数值计算。为了验证本文中计算方法的有效性和准确性,对文献[4]中的实验过程进行数值模拟,并将计算结果与实验结果进行对比。实验有2个工况,破片初速度分别为600和900m/s。数值计算模型的几何尺寸及相关材料参数与文献[4]中的一致,本文中对容器内液体用SPH描述,球形粒子直径为2.2mm,共有393 040个粒子,计算过程采用8个并行模块。计算结果与实验数据的对比如图2所示。从图2可以看出,数值模拟较准确地捕捉到了破片穿透过程中舱内液体压力ps的变化规律,但计算得到的压力峰值较实验结果小,主要是因为数值计算得到的压力是测点周围单元的平均压力。
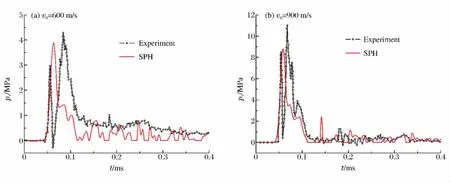
图2 在2种不同破片初始速度情况下,计算得到的P1点压力与实验结果的比较Fig.2 Calculated pressures at test point P1compared with experimental ones at two different initial velocities of fragment
3.2 数值计算模型
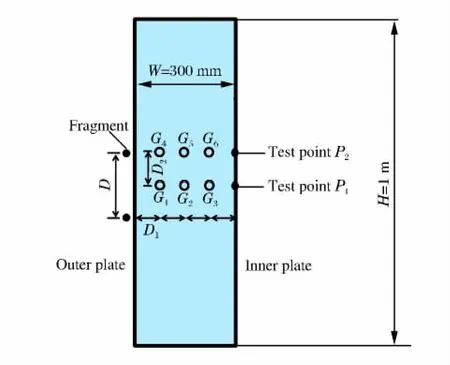
图3 液舱尺寸Fig.3 Dimension of liquid-filled cabin
本文中数值计算模型的具体尺寸如图3所示,测点G1~G6布置在舱内液体中,测点P1、P2布置在液舱内板上,D1=75mm,D2=100mm。液舱板的厚度均为5mm,材料为船用945钢。根据第1节中对反舰武器战斗部破片特性的分析结果,打击液舱所用的球形破片的质量为27.5g,入射速度v0=2km/s,破片材料为TC4。假设破片为球形且穿透液舱过程中不发生变形,则半径r=9.44mm。对舱内的液体采用SPH粒子离散,对液舱板和破片采用Lagrange体单元模拟。液体的状态方程及相关参数与文献[4]中的相同,对液舱板和破片采用Johnson-Cook本构模型,文献[15]中给出了船用945钢和TC4材料Johnson-Cook本构模型的具体参数。在计算过程中,单发破片的入射点在液舱几何中心位置,双发破片以液舱上下中心位置对称。
3.3 单个破片穿透液舱
单个爆炸破片穿透液舱的过程如图4所示,破片穿透液舱外板后冲击舱内液体,形成了半球形的冲击波并向外传播,直到冲击波在液舱内板处形成反射;此时,液舱内板在冲击波压力作用下产生变形,反射冲击波最后将作用在液舱外板上,使得外板的变形增大。破片继续在液体中运动,受到液体的阻力作用,速度迅速衰减;同时破片周围的液体受到破片的持续推动作用。破片靠近液舱内板时压缩两者之间的液体,对液舱内板产生局部压力。最后,破片穿透已有预加应力的液舱内板。
高速破片撞击舱内液体时产生的冲击波峰值压力p很高,离液舱外板10mm处的冲击波峰值压力达到5.280GPa,但随着传播距离的增加而迅速衰减,如图5所示,当冲击波传播至液舱内板附近时,其峰值压力降至0.288GPa。从冲击波峰值压力的变化趋势来看,随传播距离的增加,其压力峰值负增量逐渐减小。
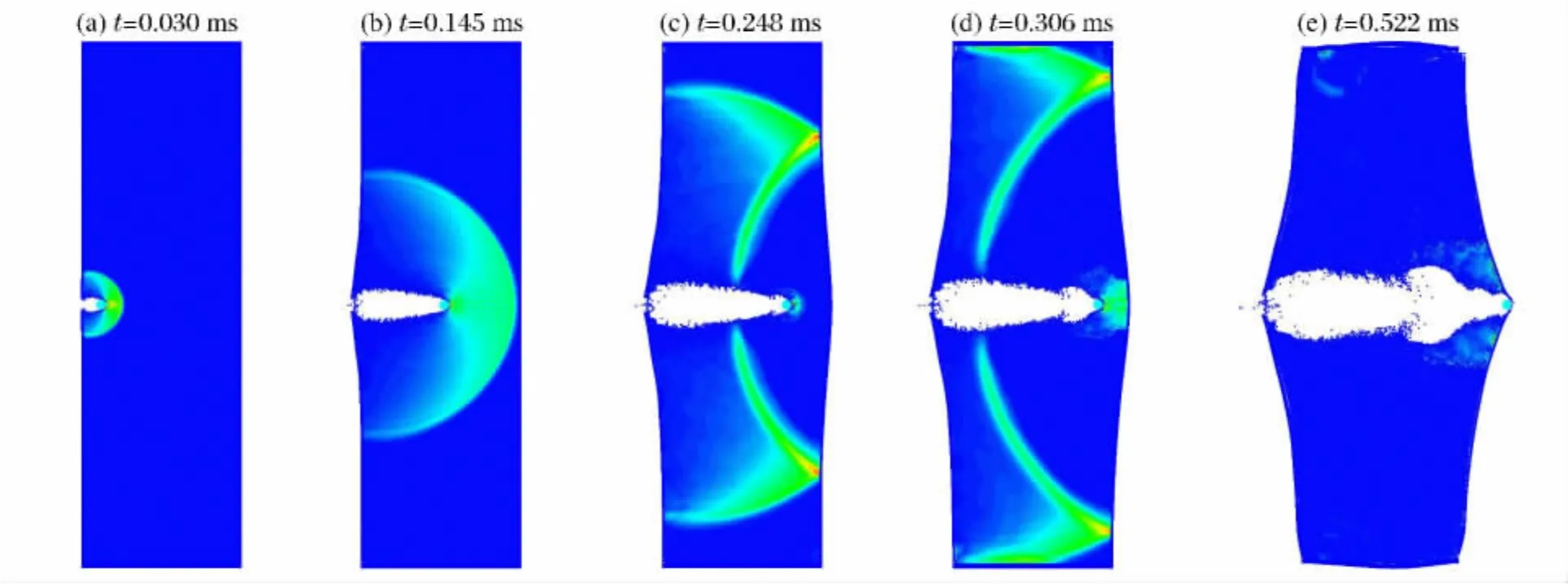
图4 单个爆炸破片对液舱的穿透过程Fig.4 Process of single fragment penetrating liquid-filled cabin
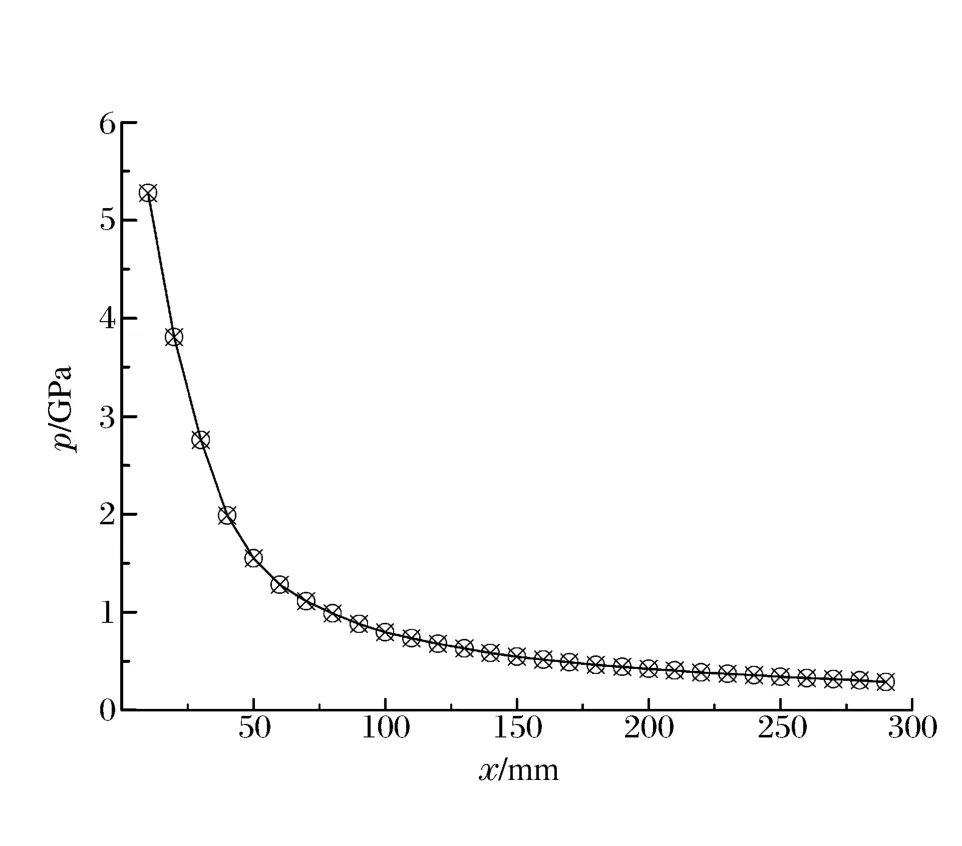
图5 冲击波峰值压力与传播距离的关系曲线Fig.5 Overpressure varied with propagation distance
破片穿透过程中速度衰减曲线如图6所示,该曲线包含5个典型特征,即破片穿透液舱外板、破片在液体中运动、遭遇反射冲击波、遭遇反射冲击波后在液舱中运动、穿透液舱内板。破片穿透液舱外板和内板过程的速度降分别为281.3和76.1m/s。另外,破片在运动过程中遭遇反射冲击波后,其速度衰减曲线近似为线性(图中虚直线为参考线),直至与液舱内板发生接触穿甲作用。
液舱内板测点P1和P2的速度响应如图7所示,当冲击波传播至液舱内板并形成反射时,液舱内板在较短时间内发生运动响应。对于测点P1,在0.19~0.28ms内速度相对稳定。随着破片与液舱内板之间相对距离的减小,液舱内板测点P1处受到局部压力作用,如图4(d)所示,以至于该测点在0.28ms后速度响应明显增大。而测点P2(与测点P1的距离为100mm)的速度响应相对平缓,即液舱内板在局部压力作用下出现明显局部变形。
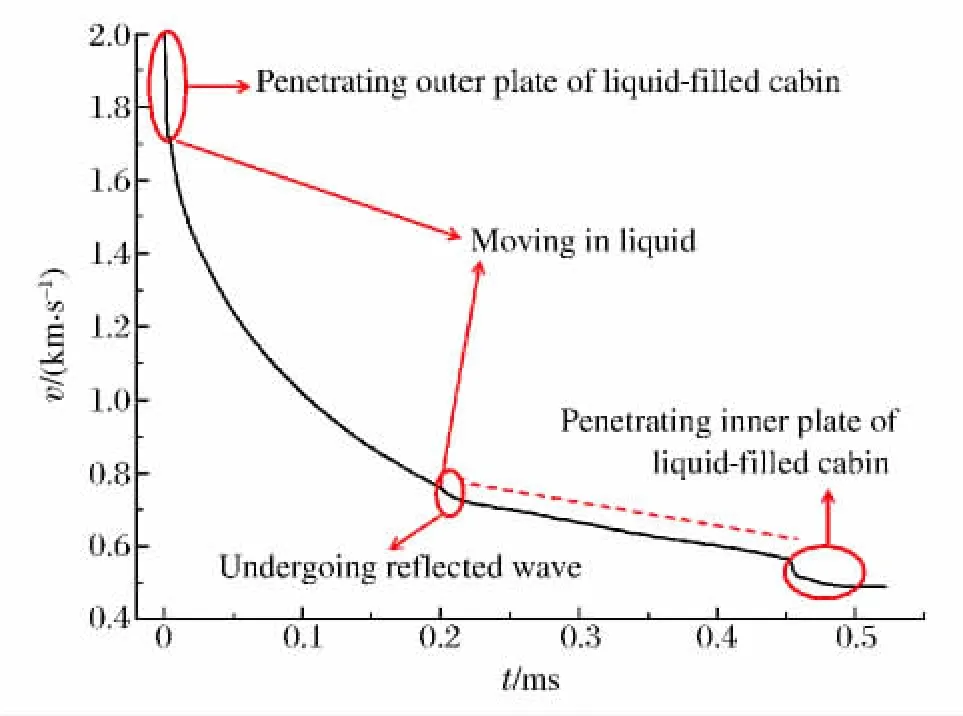
图6 爆炸破片速度衰减历程曲线Fig.6 Velocity decay curve of fragment
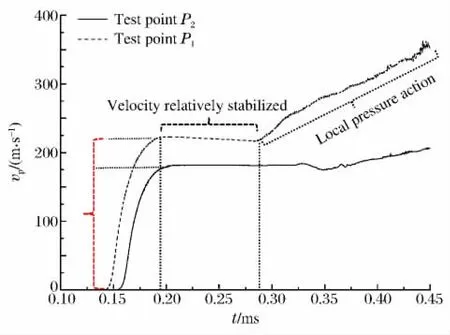
图7 液舱内板测点速度响应曲线Fig.7 Velocity response curves of test points on inner plate
3.4 双发破片对液舱的穿透过程
战斗部爆炸产生的破片空间分布较集中,液舱将受到破片群的冲击作用,破片群的密度主要与战斗部和液舱之间的距离有关。本节中以双发破片对液舱的穿透过程为研究对象,探讨破片密度(破片间距)对液舱防御效果的影响。双发破片(间距D=200mm)对液舱的冲击过程如图8所示,破片穿透液舱外板后形成半球形的冲击波,破片各自运动产生的冲击波在相遇后发生相互作用,形成双发破片的叠加冲击波。叠加冲击波的传播速度明显高于初始冲击波,其波头与初始冲击波之间的距离逐渐减小,此时液舱中最大压力出现在叠加冲击波的波头位置。随着传播距离的增加,破片形成的初始冲击波和叠加冲击波先后作用在液舱内板上,并形成反射波,如图8(d)所示。从图8(e)、(f)可以看出,叠加冲击波形成的反射波传播速度更快。
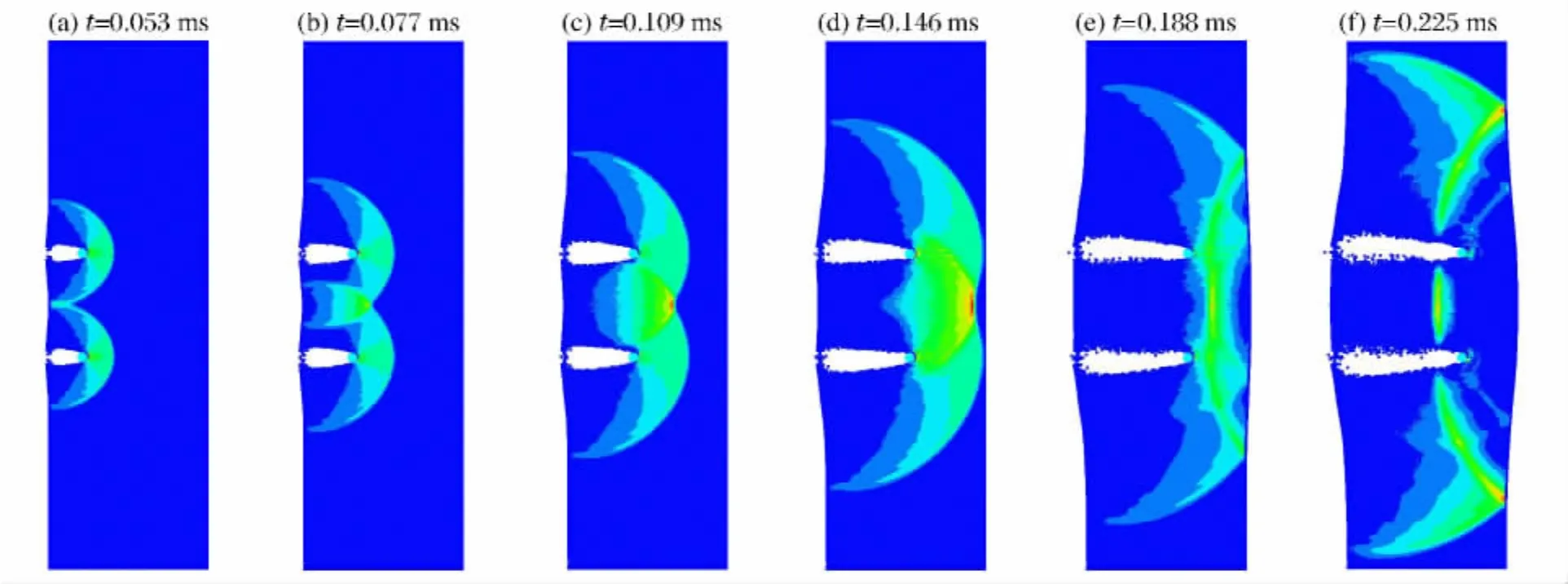
图8 双发破片对液舱的穿透过程Fig.8 Process of double fragments penetrating liquid-filled cabin
双发破片间距不同时各测点的压力与单发破片作用时压力的对比如图9所示,D/d为破片间距离与破片直径的比值,pd/ps为双发、单发破片作用时测点最大压力的比值。从各测点在不同间距的破片作用下的压力响应情况来看,对于靠近液舱外板的测点,破片间距较小时其压力响应就出现了明显的叠加,如图9(a)、(b)所示,测点G1和G2在破片间距分别为3.7和6.4倍弹径的双发破片打击下其压力响应是单发破片打击下的2.3倍。远离液舱外板的测点的压力响应则随着破片间距的增大而增大,如图9(c)所示,破片间距为10.6倍弹径时,其压力响应达到单发破片打击下的2.38倍。对于液舱内板测点P1,随着破片间距的增大,压力响应增加的趋势变缓,如图9(d)所示。
根据Hugoniot-Rankine关系,破片在液体中运动时产生的冲击波压力p与速度us的关系[3]为:

式中:ul为液体的质点速度,与破片接触的液体质点速度ul=v1;us是液体中产生的冲击波速度;c0和s分别为液体中的声速和液体的 Hugoniot因数,对于水,c0=1 470m/s,s=1.94。
由式(7)结合测点P1的压力,可得到双发破片打击时P1处液体的流动速度是单发破片打击时的1.16倍。
双发破片打击情况下液舱内板测点的速度响应曲线如图10所示,相比单发破片的打击情况,液舱内板测点P1和P2的速度响应明显增大。测点P2的速度响应较早,但随着叠加冲击波作用在液舱内板上,测点P1的速度响应迅速增大,而且响应时间长于单发破片的情况。这主要是因为双发破片打击下液舱内板响应速度增大,破片与液舱内板之间的相对速度减小,从而使破片对液舱内板的穿透延迟。
破片间距不同时,单个破片在垂直方向上的速度变化如图11所示,破片间距较小时,垂直方向上的速度较大。其主要原因是,当破片间距较小时,由于破片撞击液体产生的半球形冲击波在峰值压力较大时就发生相互作用,破片间的液体形成高压区,迫使破片产生垂直方向的运动。而随着破片间距的增大,由于冲击波压力峰值随传播距离的增大明显减小,破片间冲击波相互作用时的压力也减小,不足以对破片的运动轨迹产生明显的影响。
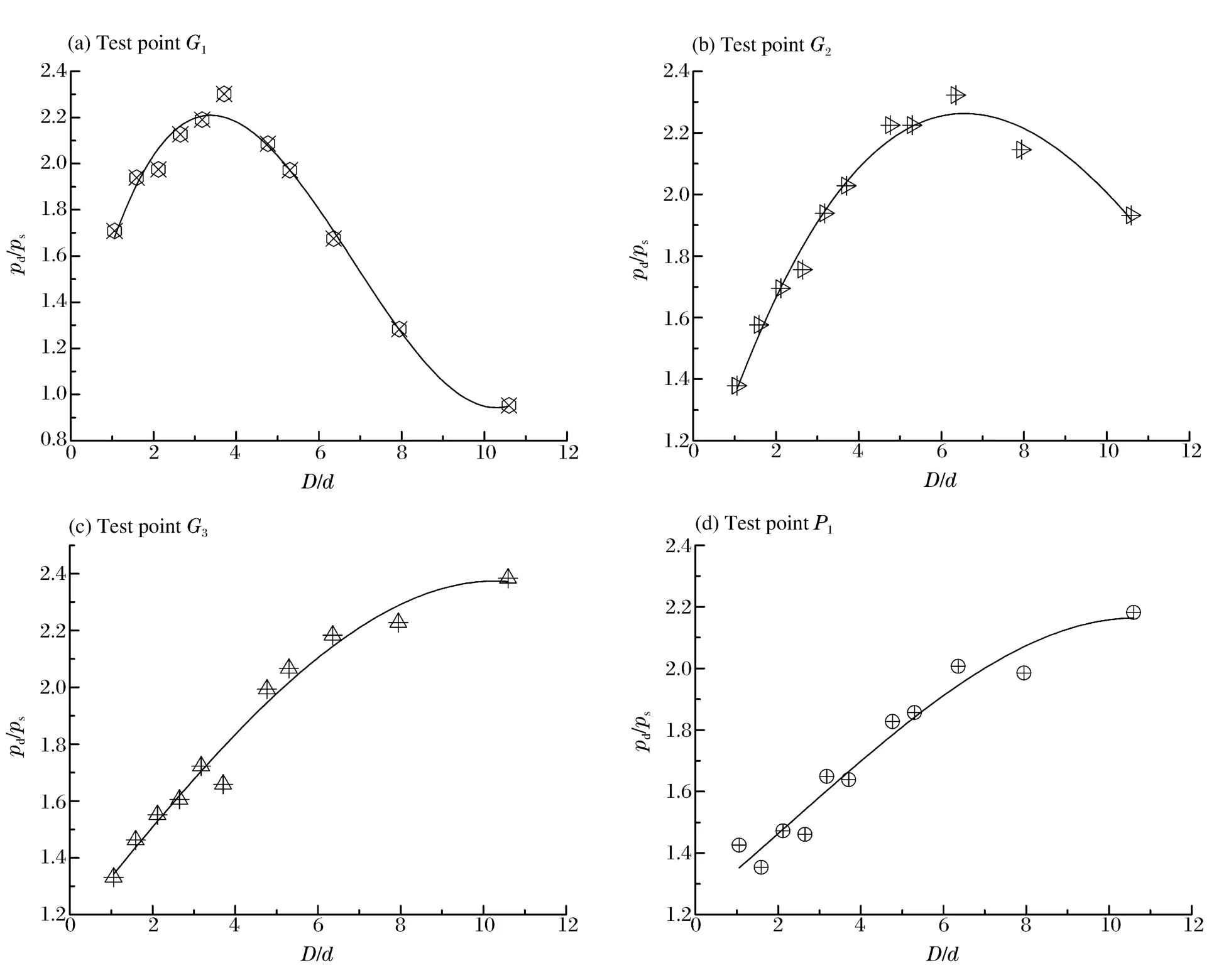
图9 各测点压力与破片间距的关系Fig.9 Relation of distance ratio and pressure ratio
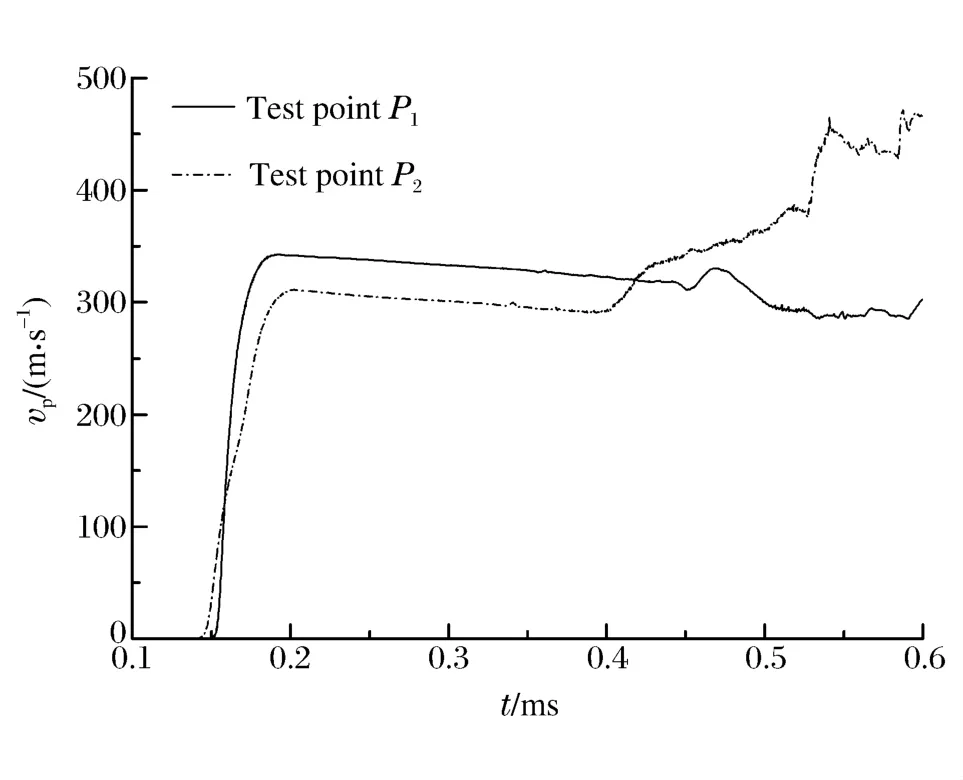
图10 液舱内板测点的速度响应曲线Fig.10 Velocity response curves of test points on inner plate
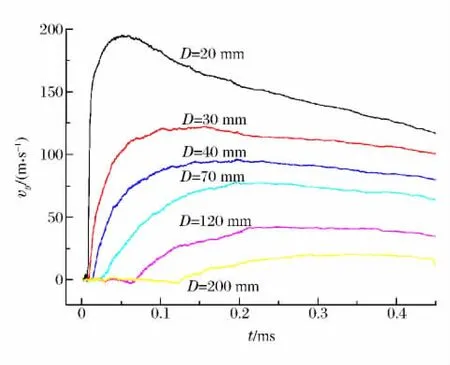
图11 不同的破片间距对破片y方向的速度影响Fig.11 y-directional velocity affected by different spaces between fragments
不同间距的双发破片穿透液舱后的速度如表1所示,破片穿透液舱后的速度与初始速度的比值随破片间距的变化较小,不同间距情况下vf/v0都在0.22~0.25范围内。单发破片穿透液舱后的速度vfs=489.7m/s,vfs/v0=0.24。从以上数据可以看出,液舱对破片速度的衰减与破片间距关系不大,其主要取决于破片在舱内的运动距离。
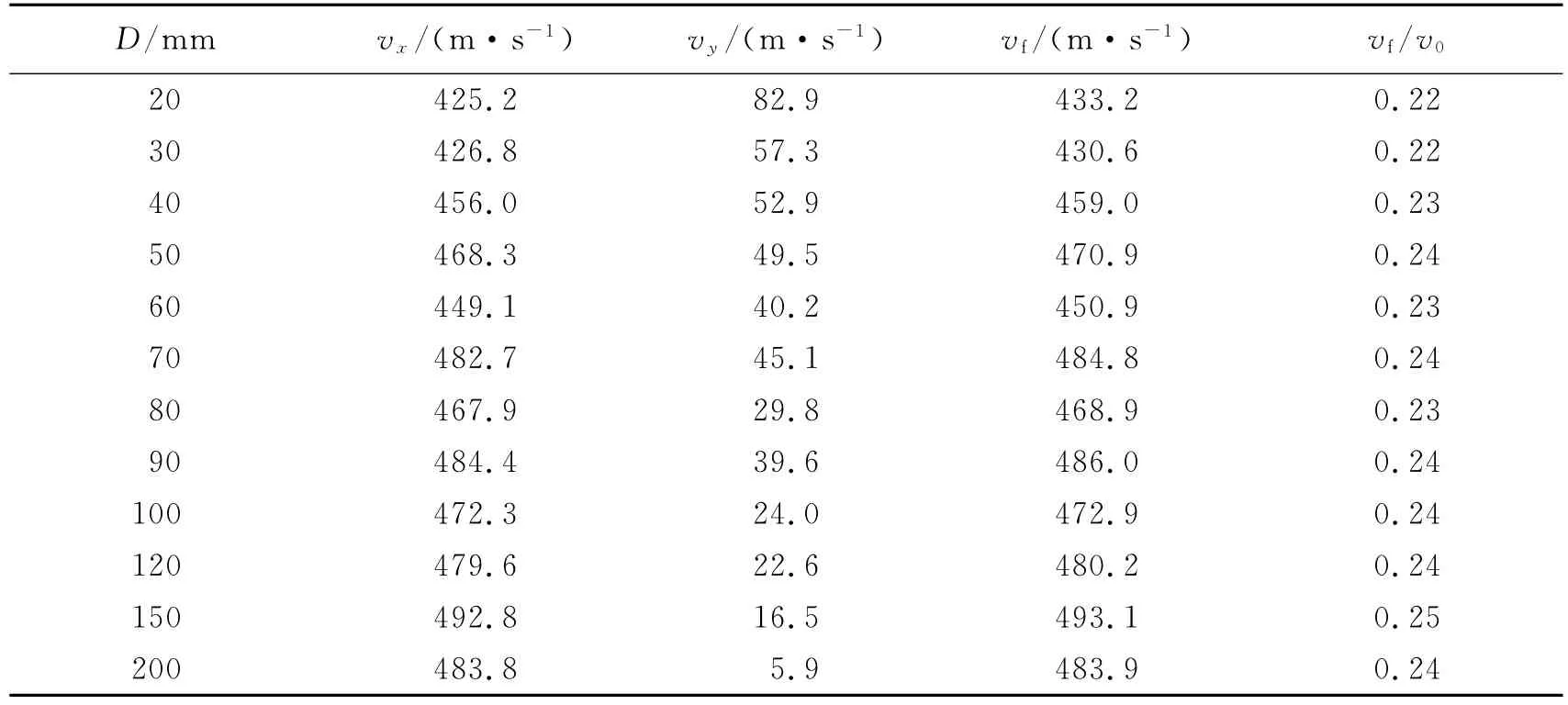
表1 不同间距的双发破片穿透液舱后的速度Table1 Final velocities of double fragments with different distances after penetrating water cabin
4 结 论
从舰船舷侧防护结构模型抗爆实验现象发现液舱对爆炸破片的吸收作用明显。破片群打击防护液舱时舱内液体中将形成强烈的冲击波和局部压力作用,防护液舱的设计中需确定其载荷作用方式和量级。本文中采用数值方法对单发破片和双发破片穿过液舱的过程进行了研究,分析了破片的速度衰减规律、舱内液体的响应及液舱内板的变形和破坏,讨论了双发破片间距对上述方面的影响。在对数值计算结果分析的基础上得到以下结论:
(1)舱内液体对破片速度的衰减作用明显,破片穿透液舱的过程包含5个典型特征,破片与反射冲击波相遇后其速度趋于线性衰减。
(2)破片在液舱内的速度衰减与舱内液体密度、破片横截面积及破片运动距离等参数相关,而液体中的冲击波压力值主要与破片的初始动能相关。由于冲击波衰减的负增量随着传播距离的增加而减小,在液舱设计时除了考虑衰减破片的速度外,应采取措施降低液体中的冲击波压力峰值,减小液舱内板受到的冲击波载荷。
(3)液舱遭受双发破片打击时,液体内部的产生冲击波有明显的叠加效应,高压区域的位置与破片间距有关;冲击波压力峰值和液舱内板受到的压力大于液舱遭受单发破片打击时的2倍。
[1]Varas D,López-Puente J,Zaera R.Experimental analysis of fluid-filled aluminium tubes subjected to high-velocity impact[J].International Journal of Impact Engineering,2009,36(1):81-91.
[2]Lee M,Longoria R G,Wilson D E.Ballistic waves in high-speed water entry[J].Journal of Fluids and Structures,1997,11(7):819-844.
[3]Townsend D,Park N,Devall P M.Failure of fluid filled structures due to high velocity fragment impact[J].International Journal of Impact Engineering,2003,29(1/2/3/4/5/6/7/8/9/10):723-733.
[4]Varas D,Zaera R,López-Puente J.Numerical modelling of the hydrodynamic ram phenomenon[J].International Journal of Impact Engineering,2009,36(3):363-374.
[5]Nishida M,Tanaka K.Experimental study of perforation and cracking of water-filled aluminum tubes impacted by steel spheres[J].International Journal of Impact Engineering,2006,32(12):2000-2016.
[6]Disimile P J,Davis J,Toy N.Mitigation of shock waves within a liquid filled tank[J].International Journal of Impact Engineering,2011,38(2/3):61-72.
[7]Borg J P,Cogar J R.Comparison of average radial expansion velocity from impacted liquid filled cylinders[J].International Journal of Impact Engineering,2007,34(6):1020-1035.
[8]Borg J P,Downs T J,Lloyd A.High strain rate fragmentation of liquid systems at atmospheric pressure[J].International Journal of Impact Engineering,2006,33(1/2/3/4/5/6/7/8/9/10/11/12):119-125.
[9]Borg J P,Grady D,Cogar J R.Instability and fragmentation of expanding liquid systems[J].International Journal of Impact Engineering,2001,26(1/2/3/4/5/6/7/8/9/10):65-76.
[10]Lecysyn N,Bony-Dandrieux A,Aprin L,et al.Experimental study of hydraulic ram effects on a liquid storage tank:Analysis of overpressure and cavitation induced by a high-speed projectile[J].Journal of Hazardous Materials,2010,178(1/2/3):635-643.
[11]Lecysyn N,Dandrieux A,Heymes F,et al.Ballistic impact on an industrial tank:Study and modeling of consequences[J].Journal of Hazardous Materials,2009,172(2/3):587-594.
[12]Lecysyn N,Dandrieux A,Heymes F,et al.Preliminary study of ballistic impact on an industrial tank:Projectile velocity decay[J].Journal of Loss Prevention in the Process Industries,2008,21(6):627-634.
[13]Szyndel M D E,Collard A D,Eyre J R.A simple relation between the detonation velocity of an explosive and its Gurney energy[J].Propellants,Explosives,Pyrotechnics,2002,27(6):365-368.
[14]Chou P C,Schaller R,Hoburg J.Analytical study of the fracture of liquid-filled tanks impacted by hypervelocity particles[R].DIT Report 160-9,NASA CR-72169,1967.
[15]徐双喜.大型水面舰船复合多层防护结构研究[D].武汉:武汉理工大学,2010:44-46.
