基于时延预测的空间遥操作系统广义预测控制
2013-09-19杨艳华阳方平李洪谊化建宁
杨艳华 ,阳方平 ,李洪谊 ,化建宁,张 峰,余 飞
(1中国科学院沈阳自动化研究所机器人学国家重点实验室,辽宁沈阳110016;2泉州师范学院应用科技学院,福建泉州362000;3中国科学院大学,北京100049;4东北大学,辽宁沈阳110014)
1 引言
空间遥操作系统为人类探索空间环境和完成复杂的空间任务提供了便利。然而,由于信号的长距离传输,空间遥操作系统的回路时延通常可达几秒甚至几十分钟[1]。对于空间遥操作,这种大时延将严重影响操作控制反馈的实时性和透明性,从而影响空间遥操作的安全性及可靠性,而且大的时变时延可能使系统失去稳定性。因此,许多学者针对遥操作系统的时延问题提出了多种控制方法[2-14]。
自从Anderson提出基于无源的控制算法以保证系统的稳定性后,很多学者将该方法应用于位置跟踪,时变时延的稳定性分析,以及许多其他的控制目标中[3-4]。然而,基于无源性理论的控制算法虽然能保证任何时延下的稳定性,但是当时延超过2s时系统透明性严重下降[5]。另一种遥操作系统的控制方法是基于H∞理论的方法,Leung和Francis等人[6]将时延建模为系统扰动,根据μ-综合设计控制器使系统满足稳定性的同时,还对这种时延扰动具有鲁棒性。文献[7-8]在假设时延有上界的情况下,设计了H∞控制器使得遥操作系统稳定,且满足给定的性能指标。这些方法都需要假定时延的上界,然后再优化一个全局目标,因此若假定的时延上界较大则得到的结果必然保守,而假定的时延上界较小却又很难适应各种实际情况。另外,日本的Imaida等人[9]采用比例微分(Proportion Differentiation,PD)控制方法在大约7s的回路时延下使得双边遥操作系统稳定,而且在ETS-VII型卫星上成功完成了斜坡跟踪和插孔试验。
由于模型预测控制(model predictive control,MPC)在补偿大时延和解决输入输出约束等方面具有很大的优势,因此学者们提出将MPC用于遥操作系统的控制中[10-14]。Sheng和Spong[10]提出了一种改进的模型预测控制方法解决遥操作系统的时延和输入输出约束问题。该方法能够提高双边遥操作系统在时延不确定情况下的鲁棒性,但是该方法只适用于固定时延的情况。2005年,Slama等[11]将广义预测控制(generalized predictive control,GPC)方法用于控制具有通讯时延和力反馈的双边遥操作系统,提出了一种时延GPC(Delayed GPC)而且将机械时延系统的Π-freeness代数性质应用于从端以实现位置跟踪。但是该方法也只考虑了固定时延的情况。2007年,Slama等又提出一种改进的GPC方法,即双边广义预测控制器(BGPC)[12]。他们将这一控制器用于具有通讯延时和从端力反馈的遥操作系统中,考虑由于实时力反馈改变了参考轨迹导致参考轨迹预先未知的情形。而且,他们采用该方法对具有从端力反馈,变时延和数据丢失等特征的比例遥操作系统进行了试验,取得了良好的控制效果[13]。陈丹和席宁等[14]针对互联网遥操作系统提出了一种基于事件的GPC方法。该方法通过寻找一个与时间无关或者非时间显函数的变量即事件作为运动参考,主端通过设计一个基于时延预测的路径管理器在线产生一个适当的预测事件,从端通过设计一个广义预测控制器计算冗余的控制信息以减小数据丢包和大时延对系统的影响。然而,这些算法要么只考虑固定时延,要么只考虑互联网的时变小时延,均忽略了时变时延大于1s的情形。而且,现有方法通常将主端和从端看作是单自由度机械臂模型[12,13],然而在实际应用中往往需要多自由度的控制。因此,现有方法在实际应用中具有很大的局限性。
本文受文献[12]和[14]启发,针对具有多自由度主从端的空间遥操作系统的大时延问题,提出一种基于时延预测的GPC方法。在主端,设计时延预测器和GPC控制器,即在文献[15]的基础上,提出一种基于稀疏矩阵的核非线性回归方法对时延进行预测。借鉴生物医学上常用的非线性相关性定义方法计算时延序列的非线性相关系数,选取与当前时延具有强非线性相关性的先前时延序列作为样本,采用核非线性回归方法预测下一时刻的时延。再将多自由度从端的动力学模型线性化,建立线性状态空间方程;操作者根据反馈的从端接触力控制操纵杆给出参考位置和速度,结合前面预测的时延,采用基于状态空间模型的方法设计GPC控制器使得系统稳定,并且满足位置和速度跟踪性能要求。在从端,设计一个非线性补偿器以补偿从端的非线性部分。最后,仿真结果表明,无论从端与环境是否接触,本文所提方法均能实现较好的位置和速度跟踪性能。
2 基于时延预测的空间遥操作系统结构
系统结构如图1所示,主端系统在地面,从端在空间站,两者之间通过网络进行通讯。因为控制器的实现需要大量硬件设备,因此将时延预测器和GPC设在主端可以避免将这些设备运送至太空所花费的巨大代价[16]。在主端,操作者根据空间站反馈的从端机械臂和环境的作用力fed(t)控制操纵杆,操纵杆输出参考位置ym(t)和参考速度vm(t)。然后,根据参考位置ym(t),参考速度vm(t),预测时延pTd(t),以及从端的时延位置反馈ysd(t),采用状态空间模型的GPC计算控制量u(t),使从端机械臂跟踪主端的参考位置和速度进行运动。因此,控制量到达从端的时延可看作是回路时延(round trip time delay,RTT)。时延预测器根据RTT的统计特征,采用基于稀疏矩阵的核非线性回归算法预测下一时刻的时延pTd(t)。在从端,非线性补偿器用于补偿从端机械臂的非线性部分,并且将从端位置及从端与环境的作用力反馈给主端。
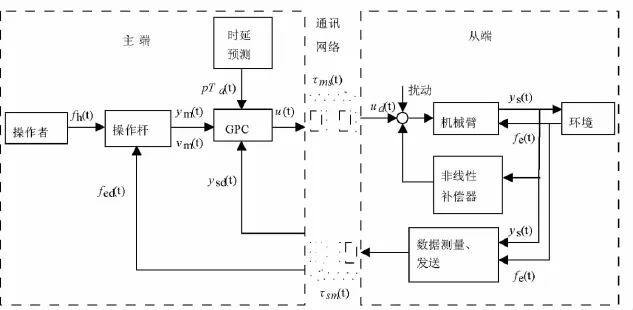
图1 空间遥操作系统结构
3 时延预测
本文提出一种基于稀疏矩阵的核非线性回归方法对时延进行预测。寻找与当前时延具有强的非线性关系的时延数据作为样本,然后根据这些样本采用基于核的非线性回归方法进行预测。这种方法比文献[15]提出的基于稀疏矩阵的线性回归方法具有更好的预测精度[17]。
借鉴生物医学领域的非线性相关性定义计算时延序列的非线性相关性[18],即若将Y看作是X的函数,那么给定X,便可根据非线性回归曲线预测Y的值。这种情况下,根据回归曲线估计出的Y方差称为解释方差(explained variance);将Y的真实方差减去由X估计出来的方差定义为未解释方差;相关系数η2表示根据回归曲线由X预测出的Y的方差的偏差。由于这个预测包含了一步非线性回归,因此可以采用两个数目有限的数据序列来估计它们的相关系数,以上系数的估计值称为非线性相关系数h2。实际上,将X分成许多小区间,对于每个区间可以计算出X的中点值pi和Y在该区间的平均值qi,回归曲线可以通过连接这些点(pi,qi)的直线段来近似逼近。那么X和Y的非线性相关系数可以写成:
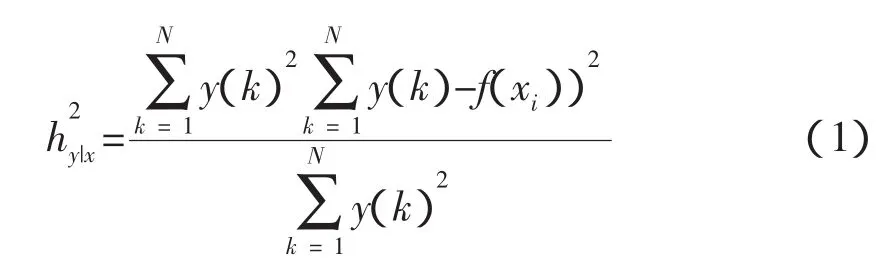
其中,f(xi)是非线性回归曲线的分段线性近似。
类似地,将X看作是Y的函数可以估计出。估计值h2∈[0,1],等于零时表明X和Y是相互独立的。若X和Y满足线性关系,那么h2是对称的,即,并且该值接近线性相关系数的平方即r2。对于非线性关系≠,而且差值Δh2表明非线性耦合的不对称程度。即Δh2很小表明X和Y是非线性关系,且X是Y的单值函数,若Δh2较大表明X和Y是非线性关系,且X是Y的非单值函数。
用式(1)计算出时延序列的非线性相关系数,然后找出与当前时延具有强非线性相关性的时延序列作为回归样本,最后采用核回归方法对下一时刻时延进行预测。
核回归方法将样本数据的特征映射到一个新的特征空间,再寻找能用线性形式表示的关系。然后,采用岭回归方法求解预测值[19]。下面简要介绍核非线性回归方法。
给定一个训练集合S={(x1,y1),…,(xl,yl)},其中xi是来自X⊆Rn的点,对应的yi是来自Y⊆Rn。X和Y为非线性关系,寻找一个非线性实值函数g(X),使之为S的最优插值。根据训练集合S,定义核函数:
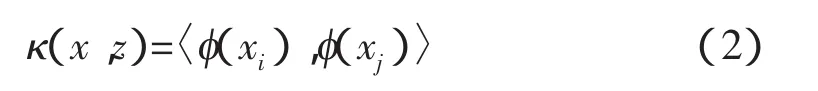
其中,φ是从X到特征空间F的一个映射,φx∈Rn→φ(x)∈F⊆RN:。选择映射φ的目的是把非线性关系转化为线性关系。φ的作用是把数据集S重新编码为S={(φ(x1),y1,…,(φ(xl),yl)}。其中 φ(xi)是来自X⊆Rn的点,问题转换为寻找一个齐次线性实值函数:
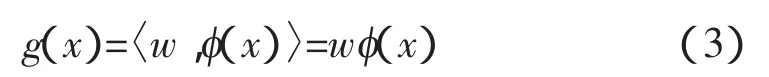
使之为S的最优插值。
定义性能指标:
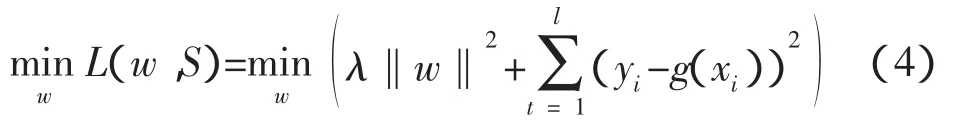
其中,w是回归系数,y是实际值,g(x)是预测值,l是样本数目,λ是一个正数,也是范数和损失之间的相对权衡,从而控制正则化的程度。将上式对w求导可得
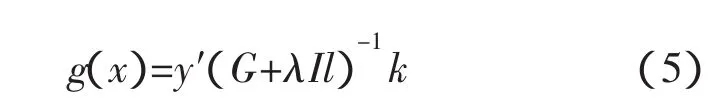
其中,Gij=〈φ(xi),φ(xj)〉。列向量k包括值:ki=〈φ(xi),φ(x)〉,i=1…l。
根据时延的特征,选取如下高斯核函数:
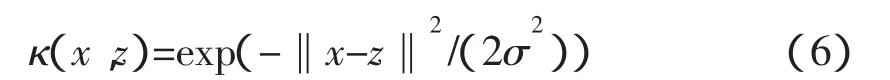
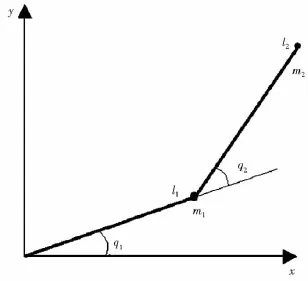
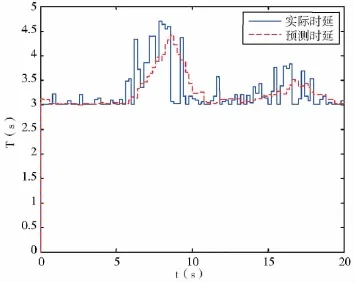
则已知样本数据根据式(5)和(6)可以预测出下一时刻的时延。但是由于时延具有长程相关性,为了解决回归自变量选择问题,借鉴文[15]的方法,将给定的一个N维RTT时间序列,按滑动窗口大小为n构造一个数组Ri=[ri-n+1,ri-n+2,…,ri(i=n,n+1,…,N;n 其中,i-n+1≤p<q 这是一种短期预测(一步预测)方法,当获得一个新时延数据,则将窗口向前移动一步,再利用前面的方法计算下一个时延。 主端和从端的n自由度机械臂动力学模型分别为: 式中,m、s分别表示主端和从端,qm(t)∈Rn和qs(t)∈Rn表示关节矢量,Dm(qm)和Ds(qs)表示机械臂的惯性矩阵,Cm(qm,q˙m),Cs(qs,q˙s)表示机械臂的哥氏力/向心力矢量,Gm(qm)和Gs(qs)表示机械手的重力矢量,Γh是操作者施加的转矩,Γs是从端机械臂的控制输入转矩,Γe是从端机械臂与环境作用力的转矩,Γed是Γe的延时。 选择适当的A21,A22使得A是稳定的。 若定义一个转矩输入为 式中(x)是f(x)的估计值,τ是时延,Δu(t-τ)是控制输入。则由(10)和(12)可得整个闭环控制系统为 式中表示函数的估计误差 此时,机械臂控制系统在关节空间被线性化,其模型可以用下面的状态方程表示 式中,w(t)是系统扰动,假设为零均值的白噪声;y(t)是从端系统输出;C表示机械臂系统输入与输出之间的关系矩阵,这里取C为2n*2n维单位阵。 对线性化后的机械臂模型(14)离散化处理,得 式中,Ad,Bd,Cd,Bwd分别对应于式(14)中的A,B,C,以及Bw经离散化后获得的系数矩阵,d是时延,d=τ/Ts,Ts是采样周期。 设在kT时刻,机械臂的优化性能指标为 系统期望的输出响应采用如下形式 其中,ξ是操作者发出的参考输入量。式中α值越小,系统鲁棒性越强,但这是以降低响应速度为代价的。 由离散模型(15)可以得到以下方程[21] 由式(18)可知,y(k+j|k)不仅与已知的控制增量Δu(k-d),…,Δu(k-1)有关,还与未知的控制增量Δu(k),…,Δu(k+j-d-1)有关。因此y(k+j|k)的预测值为 其中 由(16),(17),(20)可得 根据式(15)可以计算出j步导前输出y(k+j),由于这个导前输出是根据系统真实模型参数推导出来,而实际控制器是根据理论模型参数(估计模型参数)设计的,系统真实模型参数与理论模型参数不完全匹配,存在模型误差。设用理论模型参数计算的导前输出为y¯(k+j),则可以利用k时刻已知的模型输出误差(22)来修正。 其中,,(k+N1)分别为G,F(k+N1)的理论模型参数值;e(k)是k时刻的模型输出误差;h是误差修正系数。根据优化性能指标(16),重新计算闭环控制策略可得 图2 平面二连杆机械臂 不失一般性,主端和从端分别采用如图2所示的平面二连杆机械臂。把机械臂的每条臂看作是质量集中在末端的刚体,其质量分别为m1=1kg,m2=1kg,长度为l1=1m,l2=1m,关节角为q1,q2,转矩为 Г1,Г2。用MATLAB进行仿真,采样周期Ts=0.1s,控制周期Tc=0.2s。选择A21=diag{-1,-1},A22=diag{-2,-2},取N1=d+1,N2=N1+4,Nu=5,ρ=20*I(20),μ =10-5*I(10),其中I(i)表示i维单位阵。主从端机械臂初始状态为q1=0rad,q2=0rad,操作者的x轴fhx(t)和y轴fhy(t)作用力分别为幅值 1N,频率1Hz的正弦输入。选取前向时延和反向时延分别为回路时延的一半。实际回路时延以及预测时延如图3所示。预测时延的均值相对误差为e=0.61%,落在μ=3σ范围内的预测时延个数占总时延个数的99.97%。因此该预测方法能够较精确的预测出遥操作回路时延。 图3 实际时延和预测时延 当从端机械臂与环境无接触,非线性误差为5%时,采用本文提出的方法对大时延遥操作系统进行控制,获得的位置和速度跟踪曲线如图4所示。从图中可以看出,本文所提方法能够使系统很好的实现位置和速度的跟踪。 当从端机械臂和环境有接触时,假设环境模型为:Fe=Kex(t)+Bex˙(t),令Ke=diag{0.5,0.5},Be=diag{0.1,0.1}。采用本文所提方法对其进行仿真,系统的位置跟踪曲线以及人的操作力(fop)和从端和环境的作用力(fe)曲线如图5所示。从图中可以看出,在与环境接触的情况下且时延抖动较剧烈时,本文所提的方法可以实现较好的位置和速度跟踪。 时延问题是遥操作系统急需解决的重要问题之一。本文针对具有多自由度主从端的空间遥操作系统的大时延问题,提出了一种新的基于在线时延预测的GPC方法。主端的时延预测器能够有效地预测出下一时刻的回路时延,从而能够动态补偿网络的随机时延;根据该预测时延采用基于状态空间方法设计的GPC使得系统对于不同的时延具有较强的适应性。仿真结果表明,在时变大时延的情况下,无论从端和环境有无接触,本文所提方法均可以使系统稳定,还可以获得好的位置和速度跟踪性能。未来的研究工作,主要是根据环境和主端的模型,采用GPC方法预测将来的从端参考轨迹,以实现无时延的位置跟踪。◇ 图4 非线性误差5%从端与环境无接触时的位置和速度曲线 图5 非线性误差5%从端与环境接触时的位置和力曲线 [1]Burridge R R,Hambuchen K A.Using prediction to enhance remote robot supervision across time delay.IEEE/RSJ Int Con IROS,2009:5628-5634. [2]蒋再男,赵京东,刘宏.力反馈柔性虚拟夹具辅助遥操作.机器人,2011,33(6):685-690. [3]Nu?oa E,Basa?ez L,and Ortega R.Passivity-based control for bilateral teleoperation:A tutorial.Automatica,2011,47(3):485-495. [4]宋爱国,黄惟一.空间遥控作业系统的自适应无源控制.宇航学报,1997,18(3):26-32. [5] Lawn C A, Hannaford B.Performance testing ofpassive communication with time delay.IEEE Int Conf on Robotics and Automation,Atlanta,USA,1993:776-783. [6]Leung G M H,Francis B A.Bilateral controller for teleoperators with time delay via?-synthesis.IEEE Trans on Rob and Auto,1995,11(1):105-116. [7]Sadeghi M S,Momeni H R,and Amirifar R.H∞ and L1 control of a teleoperation system via LMIs.Applied Mathematics and Computation,2008,206:669-677. [8]Wang Y,Sun Z Q,and Chou W S.Robust controller design for teleoperation systems with time-varying delays.IntConfon Measuring Technology and Mechatronics Automation,2010:266-269. [9] Imaida T,Yokokohji Y,Doi T,et al.Groundspace bilateral teleoperation of ETS-VII robot arm by direct bilateral coupling under 7-s time delay condition.IEEE Transactions on Robotics and Automation,2004,20(3):499-511. [10] Sheng J,Spong M W.Model predictive control for bilateral teleoperation systems with time delays.Proc Can Conf Electr Comput Eng,Tampa,FL,2004,4:1877-1880. [11] Slama T,Aubry D,Vieyres P,et al.Delayed generalized predictive control of bilateral teleoperation systems.Proc 16th IFAC World Congr,2005:379-384. [12]Slama T,Aubry D,Oboe R,et al.Robust bilateral generalized predictive control for teleoperation systems.Con on Control and Automation,Mediterranean,2007:1-6. [13]Slama T,Trevisani A,Aubry D,et al.Experimental Analysis of an Internet-Based Bilateral Teleoperation System With Motion and Force Scaling Using a ModelPredictive Controller.IEEE Transactions on Industrial Electronics,2008,55 (9):3290-3299. [14]陈丹,席宁,王越超等.网络遥操作系统中基于事件的预测控制策略,控制理论与应用,2010,27(5):623-626. [15]Chen D,Fu X,Ding W,et al.Shifted gamma distribution and long-range prediction of round trip time delay for Internet-based teleoperation. International Conference on Robotics and Biomimetics,Bangkok,Thailand,2009:1261-1266. [16]Bemporad A.Predictive control of teleoperated constrained systems with unbounded communication delays.Proc 37th IEEE Con on Decision Control,Tampa,Florida,U.S.A.,1998,2:2133-2138. [17]Yang Y,Li H.Kernel Based Nonlinear Regression for Internet Round Trip Time-delay Prediction.WCICA 2012. [18]Pijn J P M,Vijn P C M,Lopes da Silva F H,et al.The use of signal-analysis for the localization of an epileptogenic focus:a new approach.Advances in Epileptology,1989,17:272-276. [19]Taylor J S,Cristianini N.Kernel methods for pattern analysis.Cambridge University press,2004.[20]Huang J,Xu L,and Frank L L.Neural Network Smith Predictive Control for Telerobotics with Time Delay.Transactions of Nanjing University of Aeronautics&Astronautics,2001,18:35~40.[21] Tang B,Liu G,Gui W,et al.State-space model based generalized predictive control for networked control systems.17th IFAC World Congr,2008,PART 1.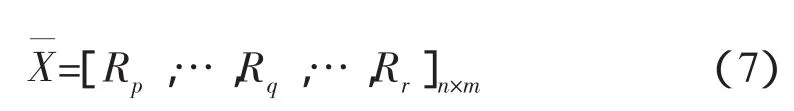
4 GPC设计
4.1 遥操作系统的线性状态空间模型
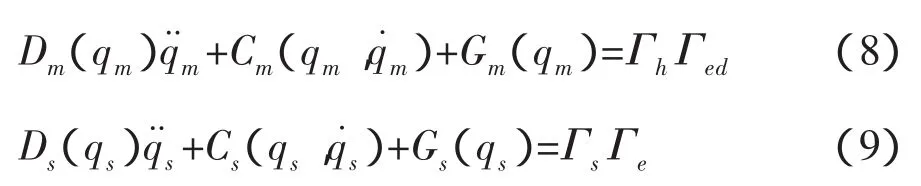
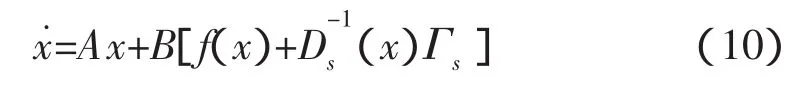
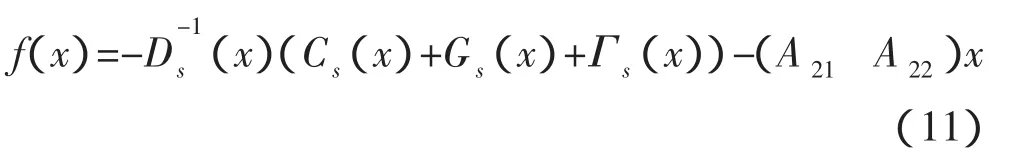

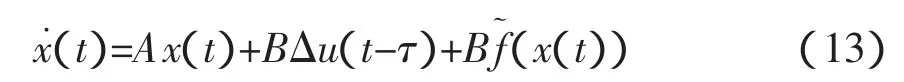
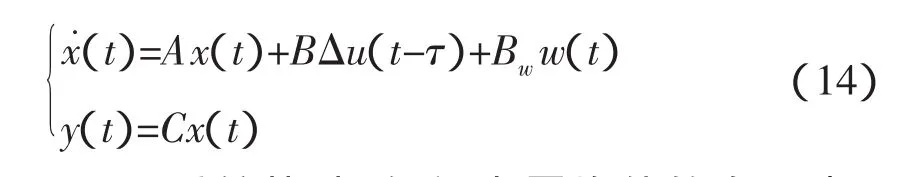
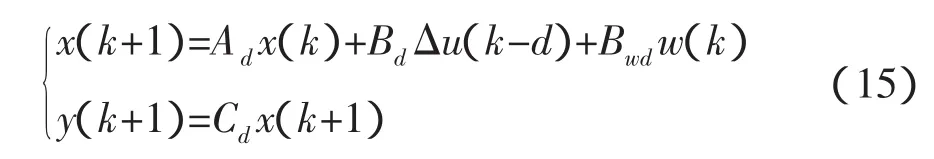
4.2 基于状态空间模型的GPC设计
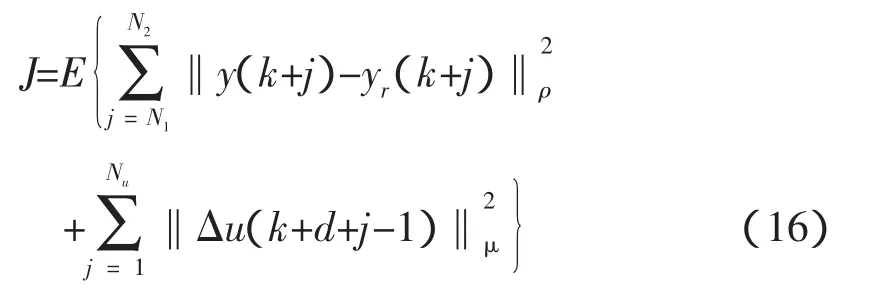
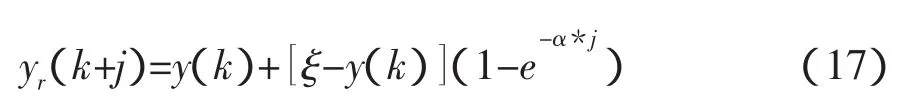
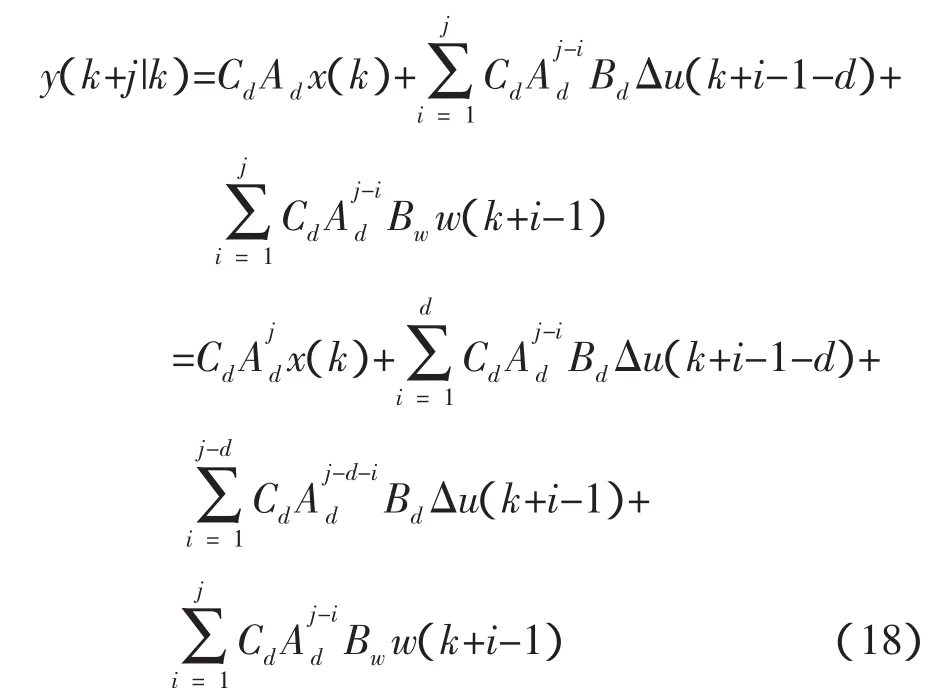
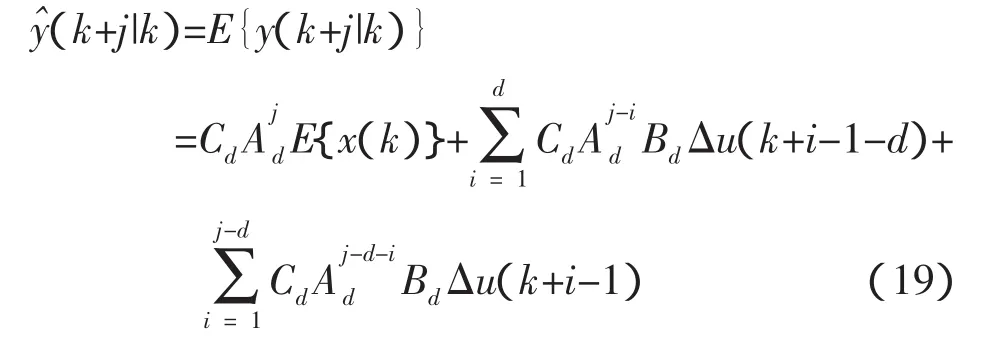
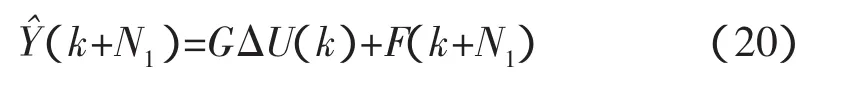

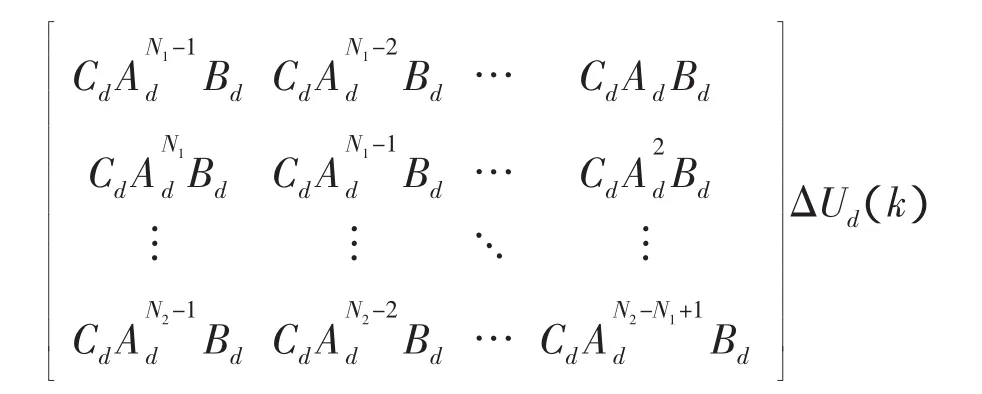
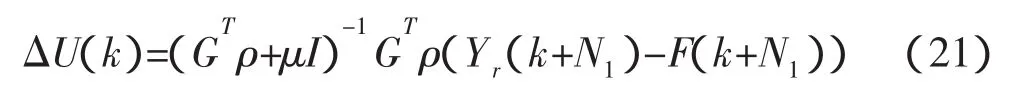
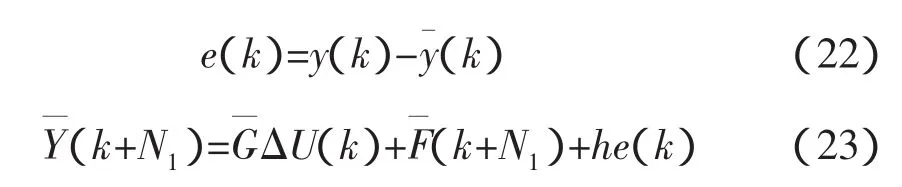
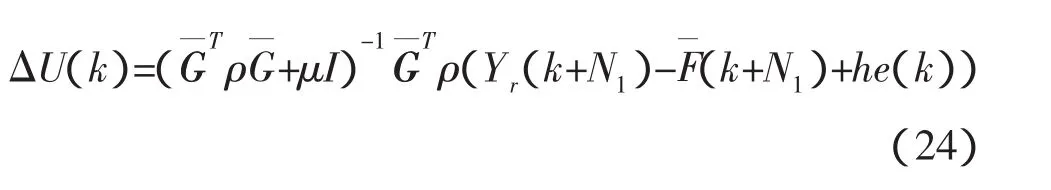
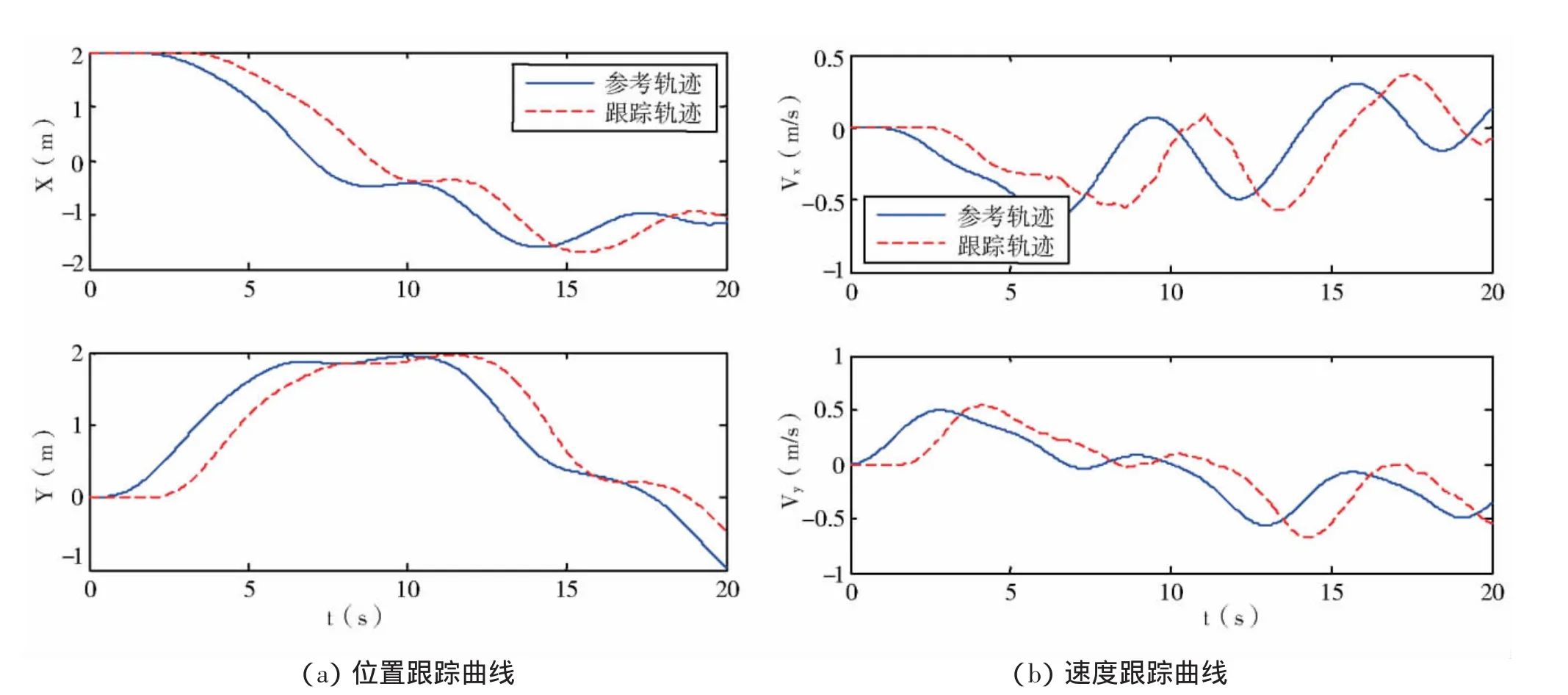
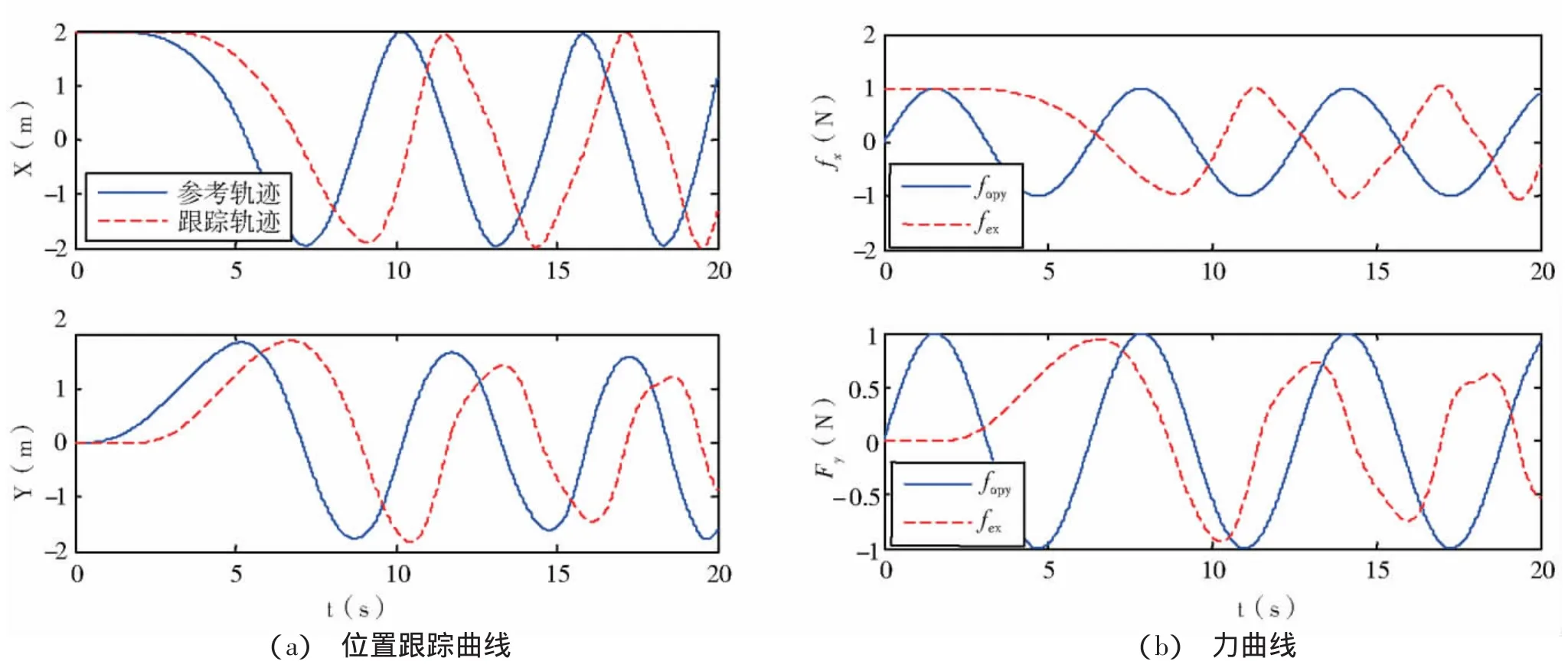
5 仿真结果
6 总结