三维感应测井仪器刻度响应有限元法数值模拟研究
2013-09-18俞燕明肖加奇柯式镇李强
俞燕明,肖加奇,柯式镇,李强
(1.中国石油长城钻探工程有限公司测井技术研究院,北京 100124;2.中国石油大学,北京 100124)
0 引言
三维感应测井目前商业化的仪器主要是斯伦贝谢公司的 Rt-Scanner[1]和阿特拉斯公司的 3DEX[1]。三维感应测井的数值模拟研究已经开展多年,主要方法有均匀场解析法[1-2]、传输线理论法[3](TLM)、有限差分方法[4-6](FDM)、有限元法[7-9](FEM)、数值模式匹配法[10](NMM)、混合势理论法[11]和有限体积法[12](FVM)等。国内外的数值模拟研究主要针对地层模型开展算法研究,对于刻度响应及其影响的计算未见到报道,相关文献主要是针对阵列感应测井仪器采用解析解的方法进行刻度环参数及刻度响应的计算[13-14]。本文针对三维感应测井仪器刻度响应进行数值模拟研究,建立了三维有限元数值模拟计算程序,并在单一倾斜刻度环下的刻度响应计算与物理实验结果进行了验证,计算考察了刻度环半径、刻度环电阻、刻度环倾斜角度、刻度环倾斜方位、刻度环水平放置位置对仪器响应的影响关系,为三维感应测井仪器刻度装置设计提供理论指导。
1 三维感应测井原理
与常规感应测井方法不同,三维感应测井采用3个相互正交的发射线圈(Tx、Ty和Tz)和3个相互正交的接收线圈(Rx、Ry和Rz)进行发射和接收(见图1),以便在各个深度点上同时测量9个磁场分量(Hxx、Hxy、Hxz、Hyx、Hyy、Hyz、Hzx、Hzy和 Hzz),再根据这9个分量计算由9个电导率分量组成的电导率张量、各向异性指标参数及裂缝参数等。
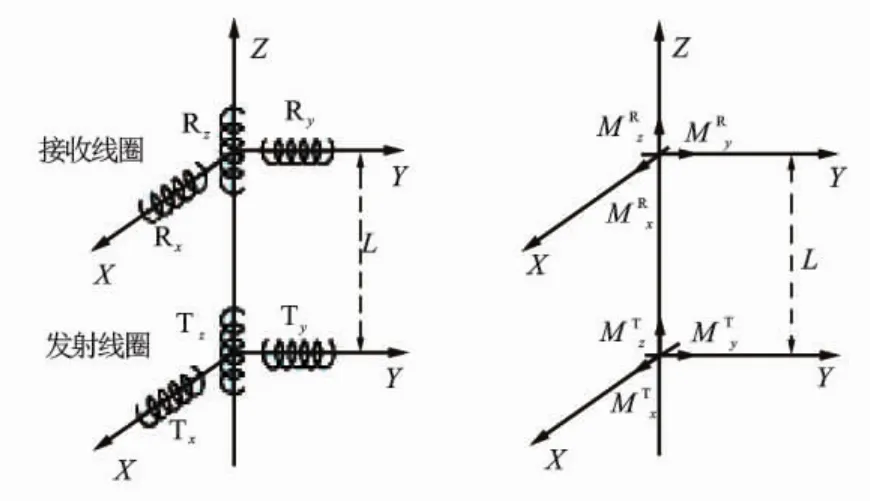
图1 三维感应测井原理示意图
对于电性各向异性地层,电导率张量的形式为
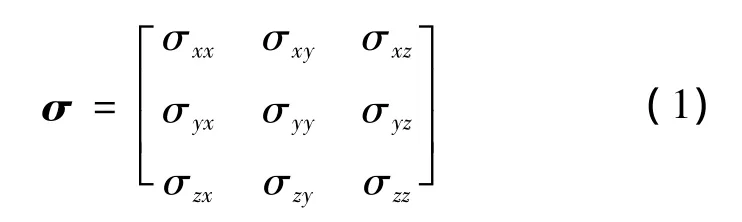
对于砂泥岩薄互层,可以等效为轴向各向异性地层,电导率张量简化为
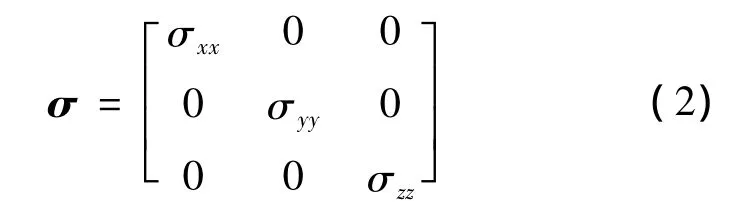
式中,σxx=σyy。
2 有限元计算方法
对于感应测井,其电磁场问题可以由Maxwell方程组描述
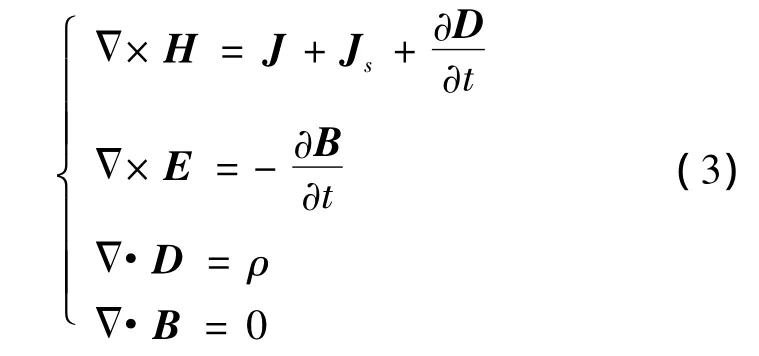
式中,E为电场强度;B为磁场强度;D为电通密度;H为磁通密度;J为导电介质体内的电流密度;Js为电流源提供的电流密度;ρ为电荷密度。状态方程
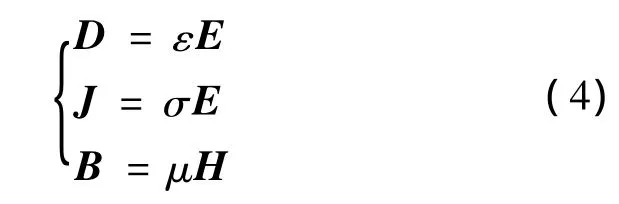
式中,ε为电容率;σ为电导率;μ为磁导率。
令

设整个求解空间被离散化成e0个单元N0个节点,对于任一节点i,在直角坐标系中,其矢势Ai的3个分量分别记为Axi、Ayi和Azi。每个单元有n0个节点,且相应于节点i的形状函数记为,则每个单元中任意点的磁矢势可表示为

根据泛函的极值求解原理可得
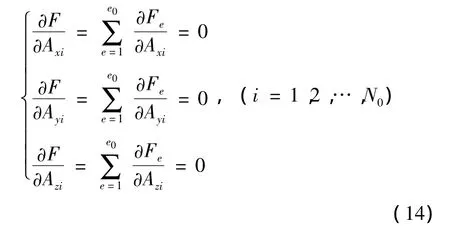
式中,对单元内的泛函偏导数的计算为
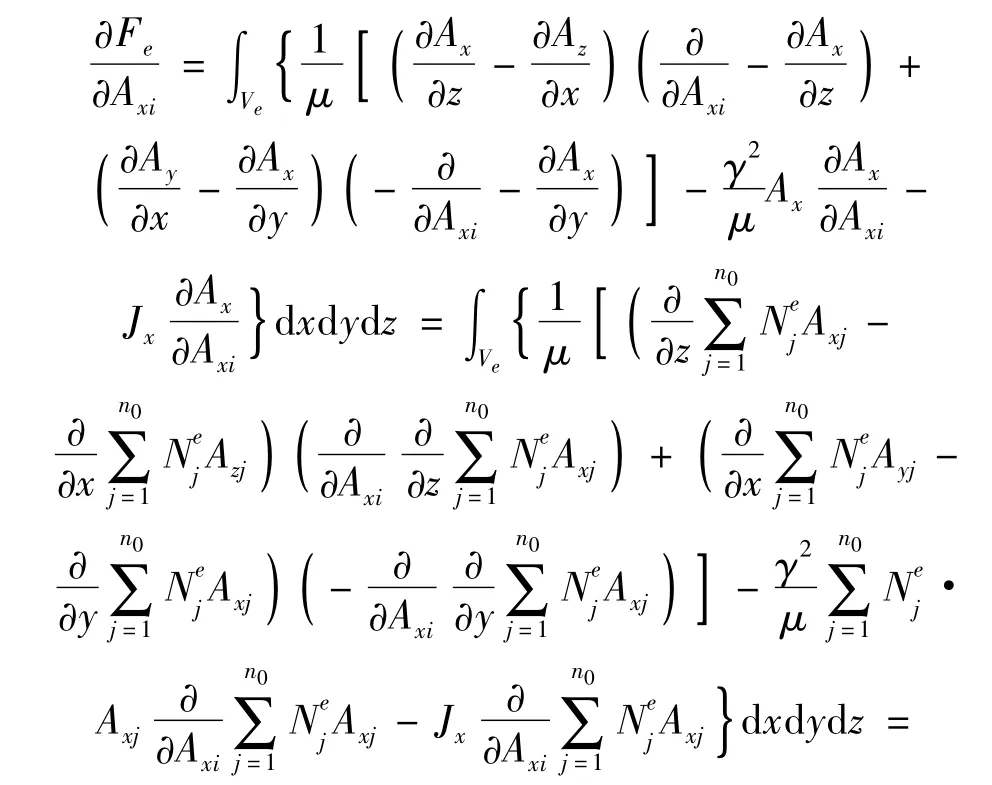

这样,对于某个单元可以计算得到单元刚度矩阵为
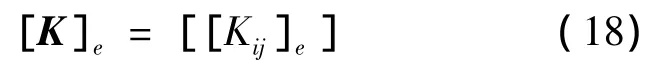
式中,

对应于单元上i节点的矩阵方程右边的常数项按式(20)计算
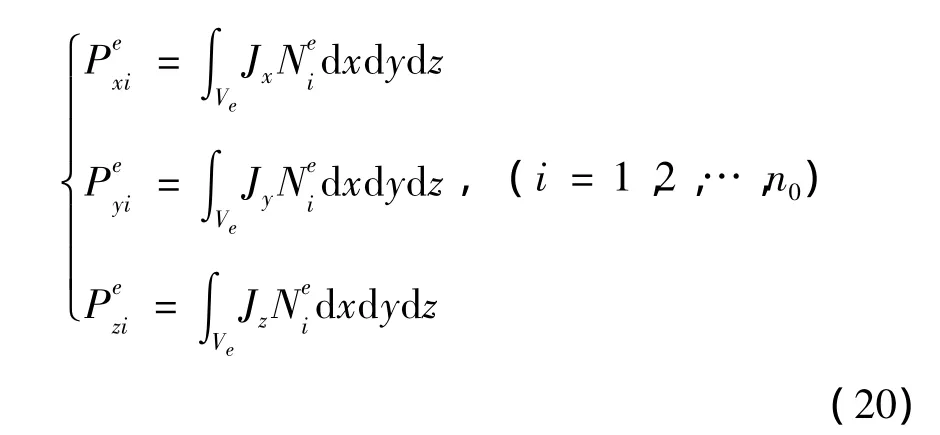
将整个求解空间的所有单元的所有节点装配完后形成了有限元求解问题的总刚度矩阵[K]及其矩阵方程

对于超大规模矩阵方程(21)的求解可以有多种算法。如直接解法中有LU分解法、LDLT分解法、GAUSS法和带状矩阵算法等。迭代法分有共轭梯度法和复双共轭梯度法等。经研究发现当线性方程组系数矩阵的条件数较差时LU分解方法最为稳定。当系数矩阵条件数中等或中等以上时,采用预条件的共轭梯度法计算速度较快,可以用于三维感应测井响应的数值计算中。
3 计算实例与分析
根据上述算法在ANSYS平台上实现了三维感应测井仪器响应的数值模拟计算,其过程是,①选择电磁功能模块。②进入预处理阶段。根据仪器参数建立有限元模型(见图2),其中圆柱块为三维感应去直耦线圈单元和接收线圈单元。最右侧的6个线圈组成了三维感应发射线圈单元。中间大的倾斜环为刻度环。其他的小线圈为普通感应接收线圈。整个线圈系中有2套由发射线圈T、去直耦线圈B和接收线圈R三线圈组成三维感应测量线圈系即浅探测和深探测线圈系,其中浅探测线圈系的发射到去直耦线圈的距离TB=0.5453 m,发射到接收线圈的距离TR=0.7620 m,深探测的TB=1.2700 m,TR=1.6002 m,发射电流和频率均为0.45 A和20 kHz,线圈匝数见表1。除了仪器模型外,还要给出地层模型,通常是圆柱体。本文因为主要是计算刻度环响应,因而介质模型中是刻度环,其半径可变,小环半径0.25 m,大环半径0.55 m,本文采用小环。刻度环之外的其他空间是半径10 m,高度20 m的圆柱体空气介质。③对所建的计算模型进行网格剖分和属性赋值。网格采用变尺度自动划分,由内到外依次变大。空气属性是电阻率无穷大,线圈属性是电阻率无穷小,不考虑涡流。刻度环当导电介质,其电阻率由刻度电阻换算成电阻率赋给。④边界条件约束和激励加载。边界条件约束主要是无穷远边界施加矢量磁位A=0。激励加载则是将电流密度加到发射线圈中。1次计算只加载1个方向的电流,分3次计算才能完成所有9个分量的计算。⑤方程组求解。给定分析类型和加载的信号频率,选择求解器,然后求解。⑥后处理。根据计算结果输出的参数,计算仪器测量信号,完成整个数值模拟计算过程。本文运用该方法开展了三维感应仪器刻度响应的计算、验证及影响因素考察。
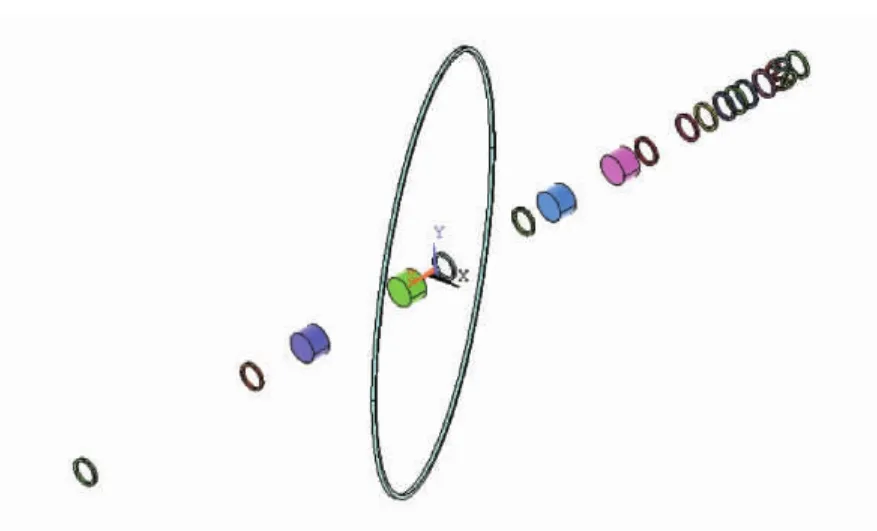
图2 三维感应仪器刻度原理示意图
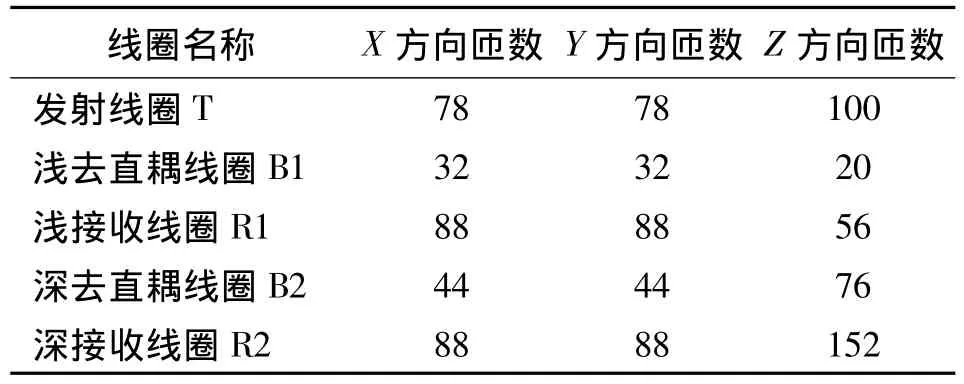
表1 线圈系中的各线圈匝数
3.1 刻度环水平放置位置的影响计算与验证
不改变刻度环的其他参数值,只改变其水平放置位置Zcal,计算出的仪器响应随刻度环水平放置位置的变化关系如图3和图4所示。由结果可以看出,对于不同探测深度的线圈系,其刻度响应取得极大值的位置不同。对于2个ZZ分量,进行了物理试验,实测的结果如图3中的实测Vr1zz和实测Vr2zz所示。Vr1zz、Vr2zz为浅、深三维感应仪器响应水平分量;比较图3的2组曲线可以看出,虽然它们在量值上存在差异(主要由于所用的频率和电流密度值存在差异引起),但曲线的形状非常一致。
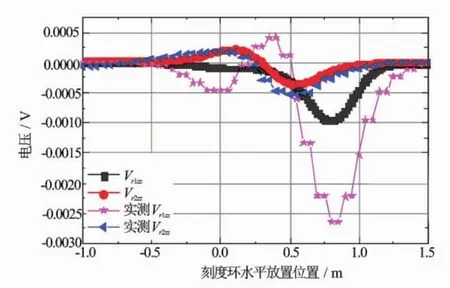
图3 三维感应仪器刻度响应水平分量随刻度环水平位置的变化及与实测结果对比
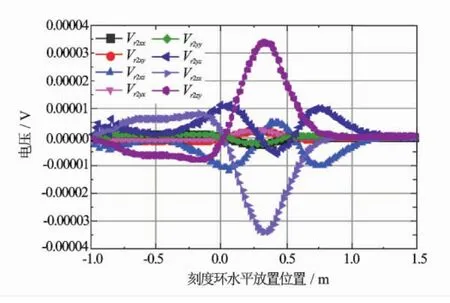
图4 三维感应仪器刻度响应非水平分量随刻度环水平位置的变化
3.2 刻度环半径的影响
刻度环倾斜角度、水平放置位置和刻度环电阻不变,只改变刻度环半径RADcal并计算仪器响应,得到浅、深三维感应测井仪器响应的ZZ分量随刻度环半径的关系如图5所示。由结果表明,一个刻度环不管其半径如何取,均无法使得2个及以上不同探测深度的线圈系同时获得最大响应,只能取折衷的半径值。
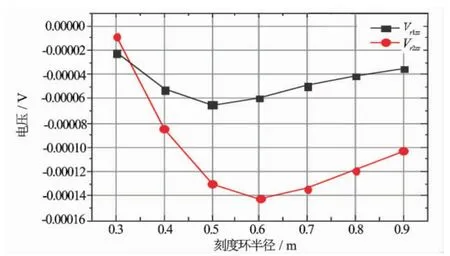
图5 三维感应仪器刻度响应随刻度环半径的变化
3.3 刻度环电阻的影响
刻度环倾斜角度、水平放置、半径等参数不变,只改变刻度环电阻Rcal值,计算出的仪器响应随刻度环电阻的变化关系如图6和图7所示。图6、图7中各分量均取绝对值进行作图,可以看出,存在使仪器各分量响应共同达到最大值的刻度电阻Rcal值。
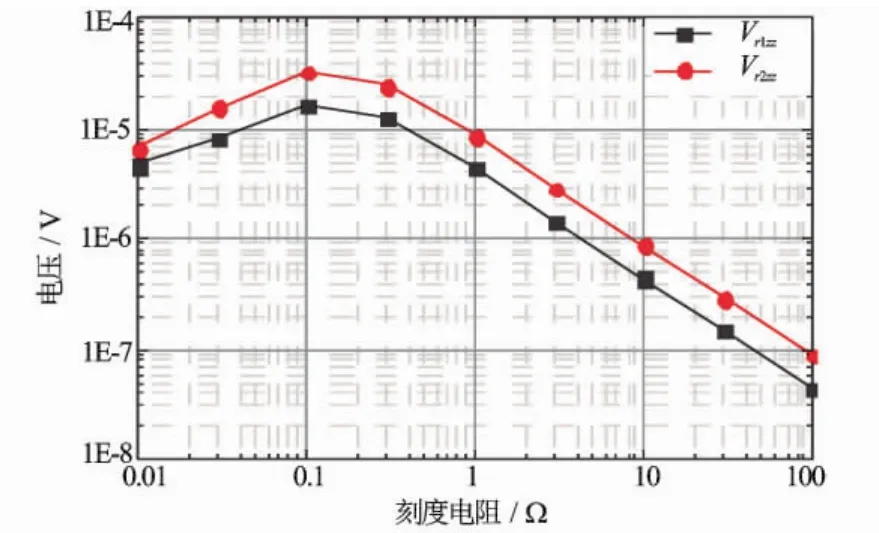
图6 三维感应仪器刻度响应水平分量随刻度电阻的变化
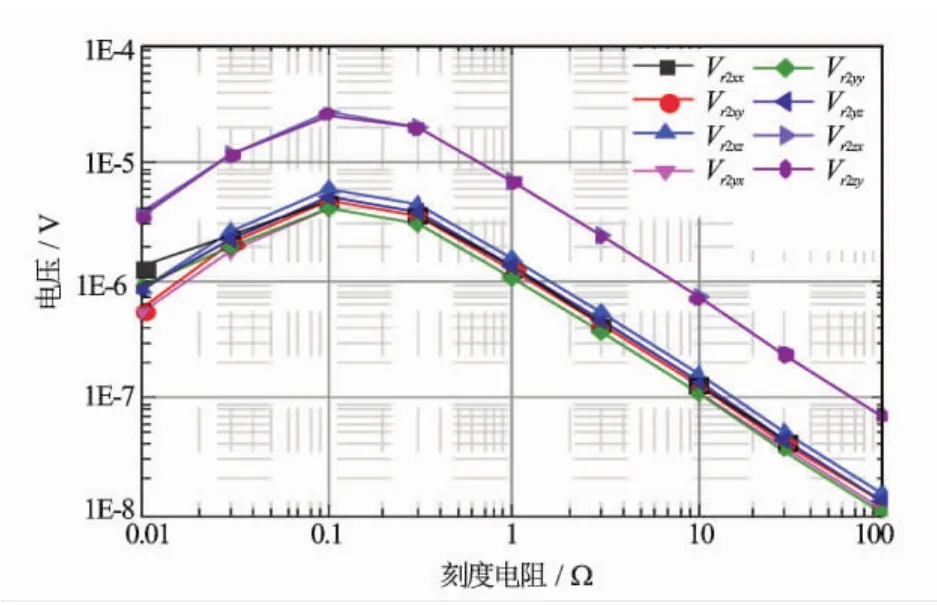
图7 三维感应仪器刻度响应垂直和交叉分量随刻度电阻的变化
3.4 刻度环倾斜角度的影响
其他刻度环参数不变,只改变刻度环的倾斜角度ALFA,计算出的仪器响应随ALFA的变化关系如图8所示。由图8可以看出,存在一个使XZ和ZX分量取得极大(小)值的ALFA。

图8 三维感应仪器刻度响应随刻度环倾斜角度的变化
3.5 刻度环倾斜方位的影响
刻度环的其他参数不变,只改变刻度环的倾斜方位XETA,计算出的仪器响应随XETA的变化关系如图9所示。由图9可以看出,XX、YY、YZ和ZY分量随方位角呈现余弦变化,XY和YX分量随方位角呈现正弦变化,ZX和XZ则呈现为半周期的余弦变化。所有分量均存在使其取得极大值的XETA值。
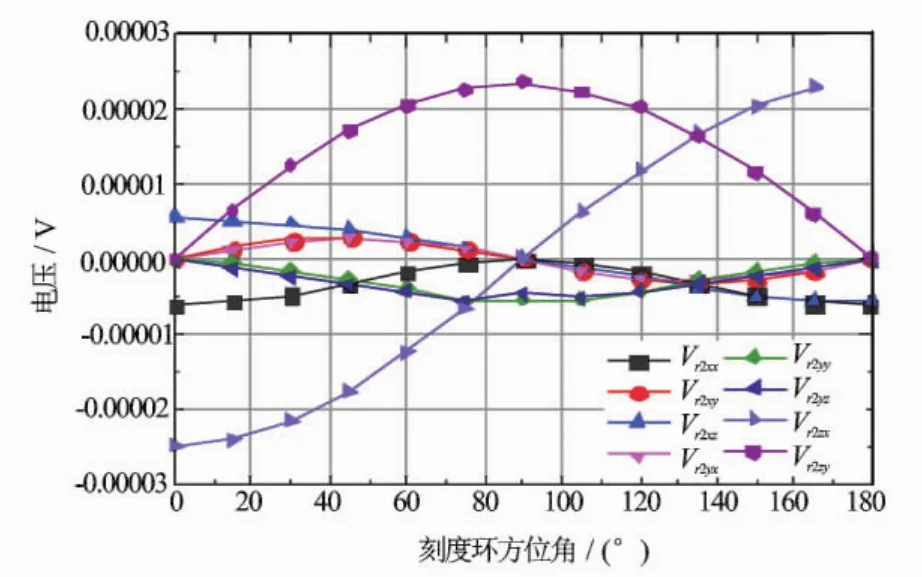
图9 三维感应仪器刻度响应随刻度环倾斜方位的变化
4 结论
(1)对于浅、深探测的三维感应线圈系,其刻度响应达到最大的刻度环的半径是不同的,因而无法确定使得这2个不同探测深度的线圈系同时达到最大响应的刻度环半径值,只能折中考虑。为此,可以考虑采用双环设计。
(2)对于不同分量取得刻度响应的极大值其倾斜角和方位角是不同的,因而要取得最大刻度响应需要针对不同的分量改变不同的刻度环倾斜角和倾斜方位来配合。
(3)对于给定半径和位置的刻度环,存在一个使其刻度响应达到极值的刻度电阻值。
(4)对于深、浅线圈系,仪器刻度响应取得极值的位置不同,刻度时应予以考虑。
[1]张国艳,肖加奇,郝永杰.三维感应测井数值计算与理论分析[J].测井技术,2012,36(1):15-19.
[2]白彦,仵杰.三分量感应线圈系在均匀地层中的响应特性分析[J].电子测试,2010,215(12):22-25.
[3]Wang H N,Tao H G,Yao J J,et al.Fast Multi-parameter Reconstruction of Multi-component Induction Well Logging Datum in Deviated Well in a Horizontally Stratified Anisotropic Formation[C]∥ IEEE Trans on Geosci and Remote Sensing,2008,46(5):1525-1534.
[4]汪功礼,张庚骥,崔锋修,等.三维感应测井响应计算的交错网格有限差分法[J].地球物理学报,2003,46(4):561-567.
[5]王昌学,杨韦华,储昭坦,等.多分量感应测井响应的交错网格有限差分法模拟[J].石油大学学报:自然科学版,2005,29(3):35-40.
[6]沈金松.用有限差分法计算各向异性介质中多分量感应测井的响应[J].地球物理学进展,2004,19(1):101-107.
[7]李飞虎,张中庆,王卓远.用矢量棱边元素法模拟三维感应测井响应[J].复旦学报:自然科学版,2009,48(5):560-566.
[8]黄临平,戴世坤.复杂条件下3D电磁场有限元计算方法[J].地球科学,2002,27(6):775-779.
[9]张继锋,汤井田,王烨,等.被动源电磁测深三维有限元数值模拟[J].成都理工大学学报:自然科学版,2010,137(6):654-659.
[10]汪宏年,陶宏根,姚敬金,等.用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应[J].地球物理学报,2008,51(5):1591-1599.
[11]Wang H N,So P,Yang S W,et al.Nummerical Modeling of Multi-component Induction Well Logging Tools in the Cylindrically Stratified Anisotropic Media and its Response[J].IEEE Trans on Geosci and Remote Sensing,2003,46(4):1134-1147.
[12]张烨,汪宏年,陶宏根,等.基于耦合标势与矢势的有限体积法模拟非均匀各向异性地层中多分量感应测井三维响应[J].地球物理学报,2012,55(6):2141-2152.
[13]仵杰,刘春雅,张甜甜,等.阵列感应测井仪刻度系数特性研究[J].测井技术,2006,30(5):400-403.
[14]张群华,范宜仁,谭宝海,等.阵列感应测井仪刻度研究[J].测井技术,2010,34(6):576-584.
