法兰螺栓联接状态空间模型及其接触参数辨识
2013-09-17田美子赵登峰曾国英
田美子,赵登峰,曾国英
(西南科技大学制造学院,四川绵阳621010)
螺栓联接在机电系统中用途极为广泛,其工作状态直接影响整个系统的安全可靠性。准确及时地识别螺栓联接状态,对于保障结构的安全可靠至关重要。近年来很多学者通过对螺栓联接结构数学模型的建立,实现模型参数辨识,以达到联接状态的识别。李以农等[1]建立了在高频情况下一维构件的波传播模型,讨论了波在其中传播的特性及能量耗散问题,提出了一种简化的螺栓接头模型;HESS等[2]采用理论和试验相结合的研究方法,针对由单个螺栓、弹簧、质量块组成的系统,建立螺栓联接的数学模型,实现了对系统松弛、压紧主要因素的研究;EL-ZAHRY[3]把螺栓法兰简化为弹簧、阻尼器、质量块的两自由度系统,研究了螺栓法兰联接结构在正弦激励载荷作用下的响应情况。以上文献均未深入探讨接触参数与螺栓预紧力矩之间的关系。
通过有限元分析方法分析被联接法兰的动态特性,将中间螺栓联接结合部简化为一系列含有接触刚度和接触阻尼参数单元,建立法兰联接结构的状态空间模型。结合法兰螺栓联接模态实验,辨识螺栓联接在不同预紧力矩下的刚度、阻尼参数,分析刚度、阻尼参数与螺栓预紧力矩之间的映射规律。
1 系统的动力学模型
文中所分析的法兰螺栓联接结构如图1所示,由材料为Q235的上、下两个筒体组成,其外径为250 mm、高度200 mm、壁厚3 mm;在中间联接部位法兰盘上均布有8个螺栓 (M6×25),均布移除4颗螺栓。

图1 法兰联结结构
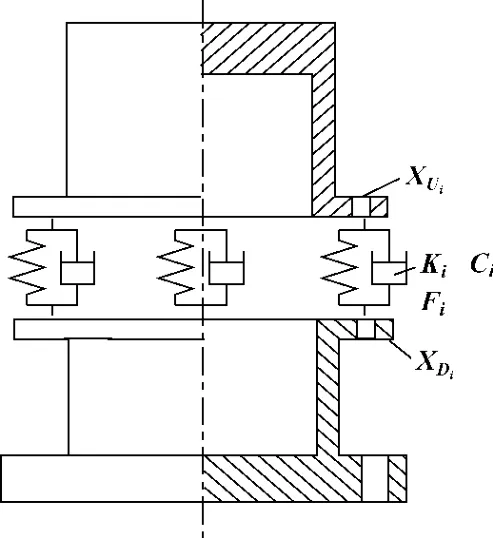
图2 螺栓联结简化模型
法兰螺栓联接结构动力学模型如图2,其中上、下两筒体由有限元模型模拟,上下筒体之间通过结合面联接在一起,这两部分之间的“结合面”可视为刚性联接。当结合面面积较小,对结合面可以用一组弹簧-阻尼来模拟其上一个自由度方向的动力学特性[4],弹簧-阻尼个数与螺栓个数相同。
1.1 上、下筒体有限元模型的建立
上、下筒体均是通过有限元计算,取前10阶模态参数的有限元模型。在COMSOL Multiphysics软件平台下,基于有限单元法,上、下筒体有限元模型如图3,然后通过COMSOL软件与MATLAB软件的接口导出上、下筒体的状态空间。

图3 上、下筒体的有限元模型
其中上筒体状态空间表达式为:

式中:X= [X1,X2,…,Xn]T为系统的状态空间向量,其中n为约简模态数的2倍,在该系统中,由于取前10阶模态参数,所以 n为 20;FU=[FU1,FU2,FU3,FU4]T为上 筒 体 上 4 个 联 接 点 (U1,U2,U3,U4)处所受的力,是系统的输入向量;YU=[YU1,YU2,YU3,YU4]T为 4 个联接点处的位移,是系统的输出向量;AU、BU、CU、DU为上筒体状态空间的系数矩阵。
下筒体状态空间表达式为:

式中:X= [X1,X2,…,Xn]T为系统的状态空间向量,其中 n 为 20;FD= [FD1,FD2,FD3,FD4]T为下筒体上 4个联接点 (D1,D2,D3,D4)处所受的力,是系统的输入向量;YD= [YD1,YD2,YD3,YD4]T为4 个联接点处的位移,是系统的输出向量;AD、BD、CD、DD为下筒体状态空间的系数矩阵。
1.2 螺栓联接环节的简化模型
如图2,中间联接环节简化为弹簧-阻尼联接,其力学关系为:
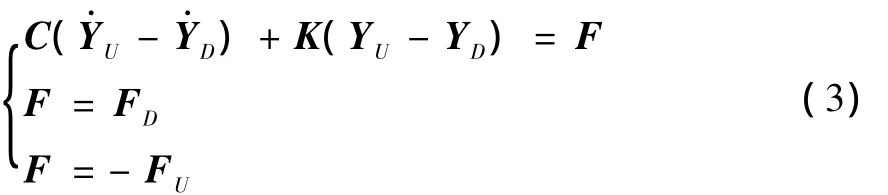
式中:K= [K1,K2,K3,K4]表示接触刚度,C= [C1,C2,C3,C4]表示接触阻尼,力F为中间结合面联接点处输出力,YU、YD分别表示上、下筒体对应联接点处的位移输出量。
1.3 整体系统的状态空间模型
图4表示了上、下筒体和中间联接环节的联接方式。M1~M4表示4个螺栓的预紧力矩,通过力矩扳手来调节。

图4 法兰螺栓联接结构系统框图
式 (4)为系统的状态空间方程:

式中:Em、En为m、n阶单位矩阵;分别为系统的状态空间向量与输出变量列阵,其中XU、XD为系统上、下筒体状态空间向量,U是系统的输入变量。
状态空间系数矩阵A的特征向量即为系统的固有频率,是构建系统状态空间模型之后容易求得的。为了参数辨识快捷方便,下文参数辨识中选取的特征量为系统固有频率。
2 实验系统
实验过程中法兰联接结构用绳子悬于空中。该实验系统采用单点激振、多点拾振的方式,用脉冲锤输入激振信号,如图5所示,移动加速度传感器用来测量法兰联接系统上各点的振动信号,两路信号经由电荷放大器送入振动及动态信号采集分析系统,分析出法兰螺栓联接系统的脉冲激励频响函数,根据频响函数得到系统的固有频率。实验过程中同时改变4个螺栓的预紧力矩,变化范围从1 N·m到10 N·m(正常工况),每次改变1 N·m之后进行一次采样,结果如表1。可见联接模型的固有频率随着预紧力矩的增强呈上升趋势。

图5 模态分析测试系统示意图

表1 法兰螺栓联接模型前3阶固有频率随预紧力矩的变化
3 参数辨识
因法兰螺栓联接结构状态方程中某些参数无法通过实验直接测量,需通过参数辨识的方法求得。文中采用结构实验模态参数频率,结合所建立的状态空间模型,采用最小二乘逼近,辨识出法兰螺栓联接结构的联接刚度K与阻尼参数C,如图6。因为此次实验同时改变4个螺栓的预紧力矩,可以近似地认为4个螺栓简化的弹簧刚度数值和阻尼参数值相等。
辨识过程中,是以螺栓联接结构固有频率状态空间模型计算结果与其实验结果的相对误差最小为原则[5]。此次辨识选取前3阶模态参数。辨识过程中的目标函数为:

辨识结论如下:
(1)结合面法向接触刚度值随着螺栓预紧力的增加不断增加。在螺栓预紧力矩较小 (1~4 N·m)时,这种增加趋势比较明显,当螺栓预紧力矩增大到一定程度 (>4 N·m)以后增加的趋势逐渐趋向平稳,如图6(a)所示。
(2)结合面接触阻尼随着螺栓预紧力矩的增加整体呈下降趋势,并且呈现出明显的非线性特性,如图6(b)所示。
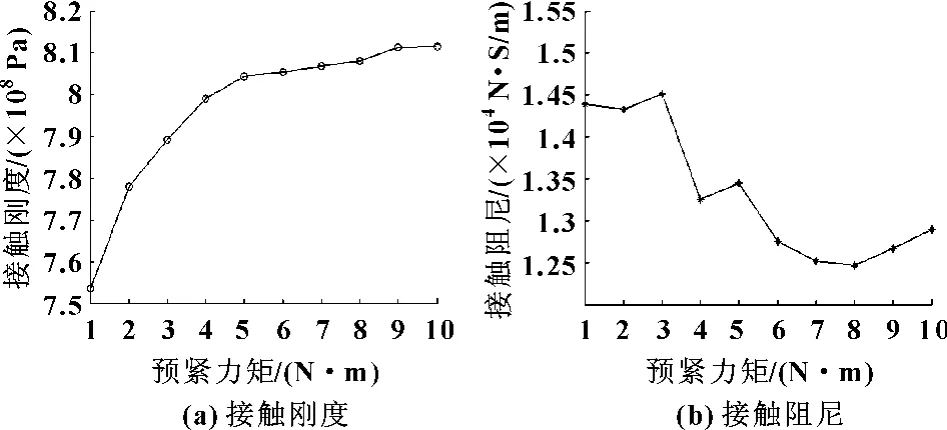
图6 接触刚度和接触阻尼参数变化
4 结论
(1)螺栓联接结构状态空间方程形式固定,具有一定的通用性,也能适用于其他类型的联接结构,只需改变被连接部分的状态空间模型即可,并且相对其他有限元模型求解快、易收敛。
(2)利用参数识别方法,可识别出各种结合条件下的接触刚度和接触阻尼,进而得出接触刚度和接触阻尼随螺栓预紧力矩的变化规律,可看出接触刚度随着预紧力矩的增加不断增加,而阻尼则是呈下降趋势,并且呈现一定的非线性,为联接结构动力学模型的建立和动态特性的分析奠定了基础。
法兰螺栓联接结构在不同预紧力矩作用下,其振动试验的接触面的随机分布不同,对接触刚度和阻尼的运动状态影响极大,对类似于此的螺栓联接状态难以准确描述;但是要弄清频谱峰值数目、幅值、峰值的分布、频谱的宽度等特征与联接接触状态的关系,除了修正状态空间数学模型修正之外,还需结合参数辨识方法[6]进行相应研究。
【1】李以农,郑玲,闻邦椿.螺栓接头非线性模型及其波能耗散[J].振动工程学报,2003,16(2):137 - 142.
【2】HESS D P,SUDHIRKASHYAP S V.Dynamic Loosening and Tightening of a Single-bolt Assembly [J].Journal of Vibration and Acoustics,1997,119(3):311 -316.
【3】EL-ZAHRY R M.Optimum Design of Preloaded Bolted Joint under Harmonic Excitation[J].Journal of Sound and Vibration,1986,108(3):455 -470.
【4】陈学前,杜强,冯加权.用非线性优化法识别接触刚度和接触阻尼[J].天津商学院学报,1989,9(1):1 -7.
【5】赵登峰,曾国英.振动环境中螺纹联结松动过程的研究[J].振动与冲击,2010,29(10):175 - 178.
【6】陈新,周济,余俊.组合结构结合部动态参数的实验识别方法[J].实验力学,1993,8(4):369 -374.
