基于现场观测的拉索风雨振参数特性分析

禹见达，吴小希，胡佳星

（湖南科技大学 土木工程学院，湖南 湘潭 411201）

随着经济的快速增长，大跨度斜拉桥的建设日趋广泛。由于斜拉索的柔度大、质量轻、阻尼系数小，大幅振动导致索锚结合处疲劳损伤，使拉索的使用寿命缩短，这引起了众多学者的关注[1-5]。由于拉索风雨激振问题涉及气体（风）、液体（雨）和固体（拉索）的耦合，从而使问题变得复杂。现场观测试验是最直接获得拉索风雨激振特性的方法，结果具有可靠性。

2012年4月，本课题组对岳阳洞庭湖大桥开展了斜拉索风雨振现场的观测试验，并取得了实测数据，据此，对引起拉索风雨振的因素作定量和定性的分析。

1 拉索风雨振的运动特征

1.1 试验现场及设备

洞庭湖大桥位于洞庭湖与长江接口处，东西走向， 双向4车道，是我国第一座三塔双索面斜拉索大桥，主桥跨径布置为130m +310m +310m +130m，主桥示意图如图1所示。

图1 洞庭湖大桥主桥示意图Fig.1 The main bridge diagram of Dongting Lake Bridge

由于大桥的地理位置特殊，拉索在北风作用下容易产生风雨振动。桥东侧中塔的S20索（参数见表1）上的磁流变阻尼器被拆卸。沿S20索距防水帽8.14m处安装面内、面外加速度传感器，见图2a，使用DH5938振动测试仪实现信号的放大和转换，采样频率为100Hz。桥面安装三向超声风速仪记录风场的全过程，见图2b。用自制雨量计（接水漏斗直径200mm）每隔5min进行一次降雨强度测量，见图2c。

表1 S20拉索基本参数Table1 The basic parameters of cable S20

图2 仪器安装示意图Fig.2 The diagram of instrument installation

1.2 拉索的振动模态

无雨时在紊流的作用下，对拉索S20振动的全过程作频谱分析[6]，结果如图3所示。由图可知，拉索面内、面外的振动均以高阶频率振动为主，低阶频率成分较少且能量较低。

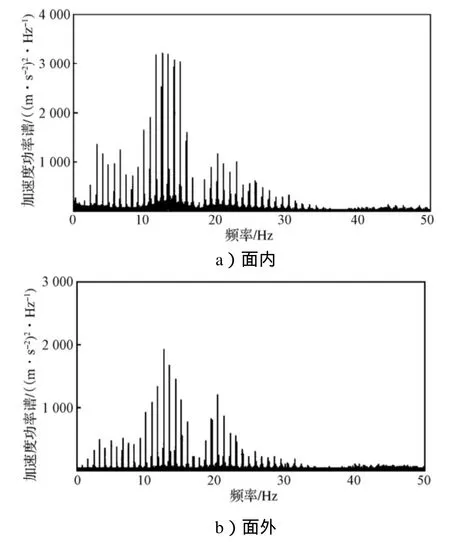
图3 S20拉索无风雨振功率谱Fig.3 Power spectrum for no-wind-rain induced vibration of cable S20

S20拉索在2次风雨振作用下的频谱分析结果如图4。由图可知，每次风雨振时拉索面内、面外都以同一阶固有频率振动，高阶频率成分很小，能量高。图4a与图4b中，振动的主导频率为2.58Hz，与拉索的基频相比，2.58Hz相当于第四阶频率，其他频率成分很小。图4c与图4d中，除第四阶模态频率外，第五、六阶模态频率成分也包含在面内加速度响应中，这可能与拉索本身的特性有关，振动模态随着拉索长度的增加可由一阶扩展到四阶以上。试验中，拉索以第四或第五、六阶模态振动，这与陈政清[6]等人观测到的风雨振时拉索的模态频率介于1～4Hz之间相吻合，但随着拉索长度的增加，这一规律是否依然存在，有待今后对更大跨度斜拉桥的观测来证实。

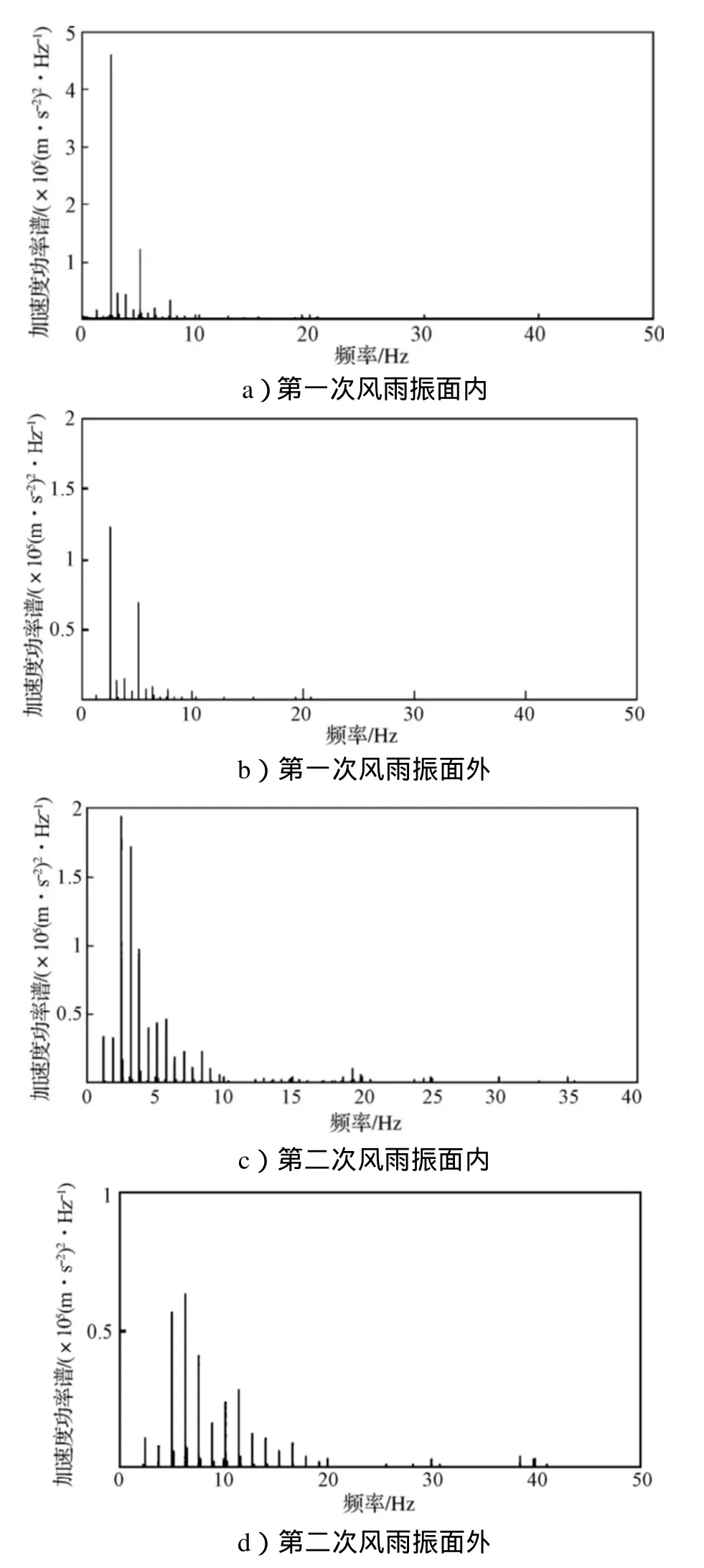
图4 S20索风雨振功率谱Fig.4 Power spectrum for wind-rain induced vibration of cable S20

1.3 拉索的等效模态阻尼比

根据随机减量技术原理[7-8]，全响应=初始位移响应+初始速度响应+激励响应。随机信号曲线最后转化为一条表示结构对初始位移自由衰减的曲线，如图5a所示。对原有采样数据（如图5b）进行海明窗口滤波与随机减量法分析后，得到滤波后的频谱图（如图6a）与自由衰减曲线（如图6b），对自由衰减曲线进行拟合，得出第四阶等效模态阻尼比为0.036 7%，结果如图6 c所示。

图5 随机减量技术原理图Fig.5 Schematic of the random decrement technology

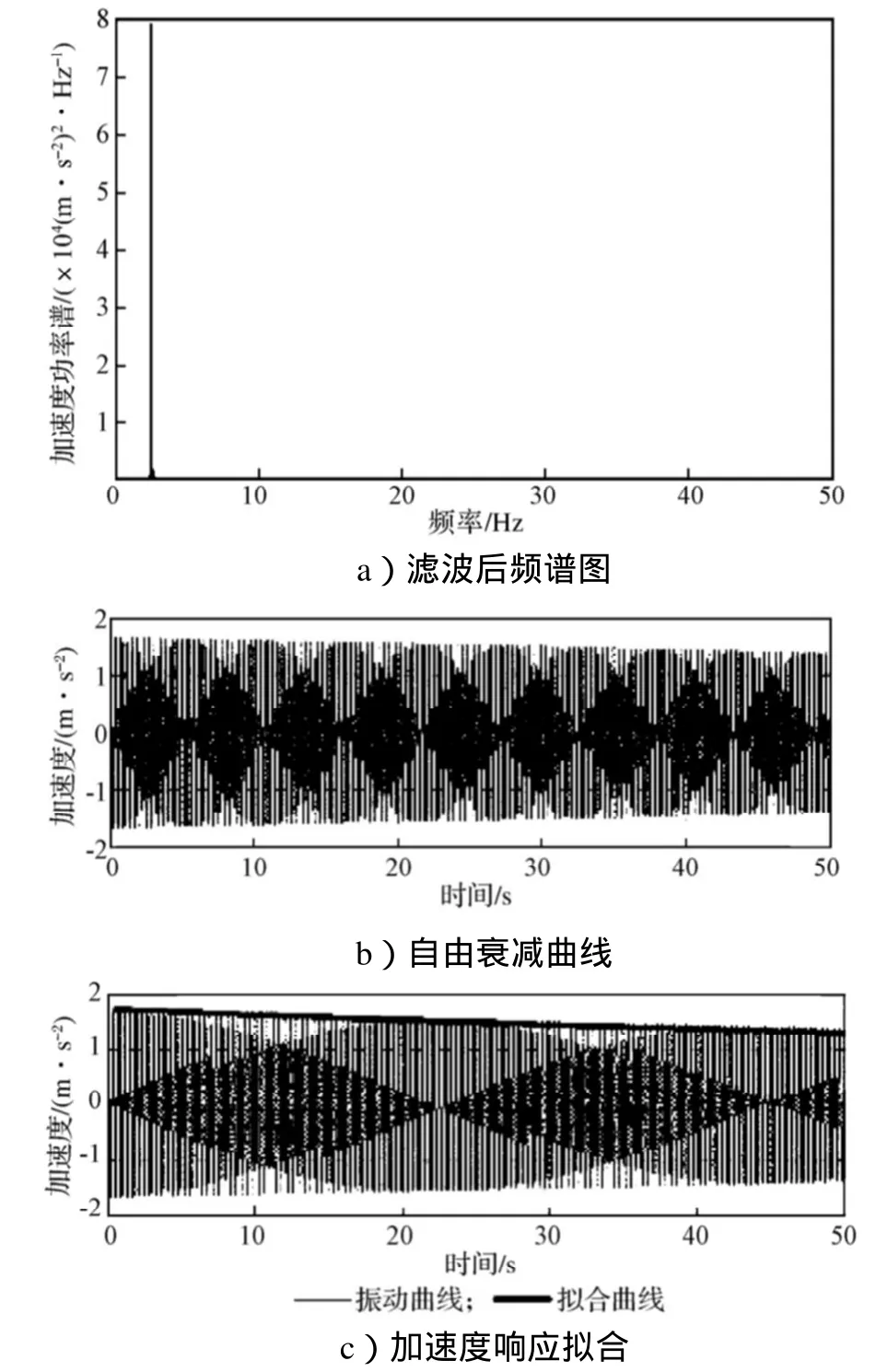
图6 样本信号的自由衰减曲线与拟合Fig.6 Free attenuation curve and fitting of sample signals

2 风速、风向角、雨量对拉索风雨振的影响

2.1 风速

S20拉索在风雨振过程中，其振幅与风速的关系见图7。由伯努利方程[9]可知，作用于物体表面的风压力与风速平方成正比，拉索振动能量的主要来源是风压力。由图可知，拉索的起振风速为5m/s，当风速小于5m/s时，风雨振未能形成；当拉索大幅振动时，风速在6m/s以上。由于S20的阻尼比小，拉索振动在第五阶模态上有发散振动的趋势，从时程图7分析可看出，风速是风雨振的决定要素之一。

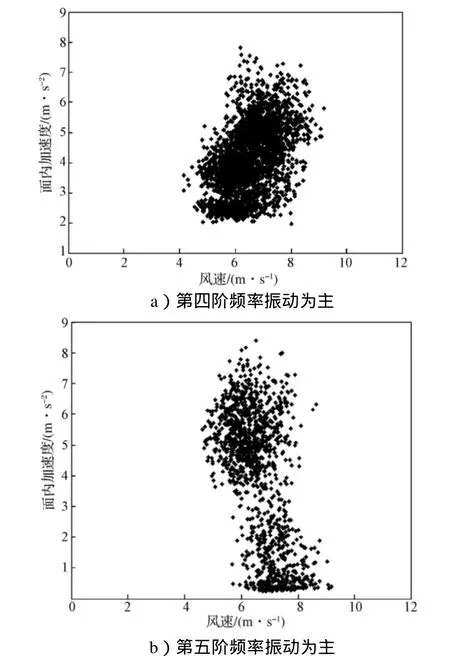
图7 S20索振幅与风速的关系Fig.7 Vibration amplitude of cable S20 vs wind speed

2.2 风向角

从动力学角度看，风对索结构作用的大小与风向角有关，主要通过有效风速来体现。S20拉索在风雨振过程中，其振幅与风向角的关系见图8。由图可知，拉索以第四阶或第五阶模态发生大幅振动时，振动的范围集中在35°～55°角之间，当风向角小于20°或大于70°，其大幅振动的情况罕见，这与Y. Hikami等人[1]的观测结果一致。风速的有效性与风向角密切相关，在实际中，尽可能避免索面与风向成90°角，这对斜拉索的减振有重要意义。

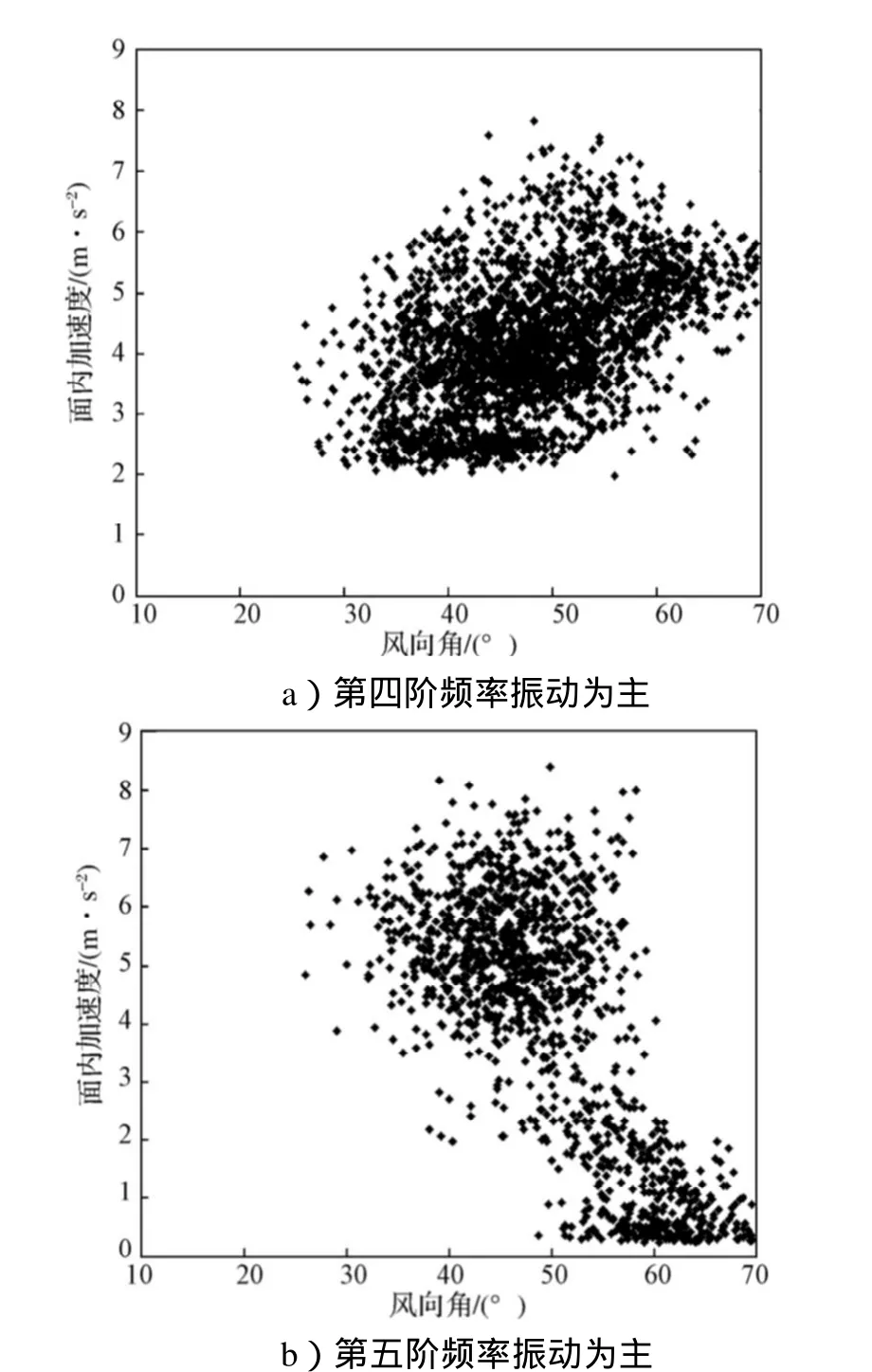
图8 S20索振幅与风向角的关系Fig.8 Vibration amplitude of cable S20 vs yawing angle

2.3 雨量

目前，学者们基本认同拉索风雨振形成的根本原因是上水线的存在；没有水路时，斜拉索难以产生规则的大振幅振动。

在风雨振现场，每隔5min记录1次降雨量，将降雨强度分3个等级：0mL为无雨，0.1～0.2mL为中雨，0.2mL以上为大雨。不同雨量下，风速、风向角与面内加速度之间的耦合关系，见图9～10。

由图9a和10a可知，拉索S20只在风荷载的作用下振动幅度很小，能在较大的风速范围内引起振动，拉索振动呈典型的发散趋势，这可能与阵风有一定的关系，是否与其他因素有关有待进一步研究。

由图9b和10b可知，拉索S20在中雨作用下有典型风雨振的特性，大幅振动的风速在6～10m/s之间，风向角在30°～50°之间，这与风雨振发生的条件基本相吻合。

由图9c和图10c可知，在大雨作用下，观测时拉索可见明显下水线，拉索的振动幅度比中雨时小很多。风雨振的发生主要条件是小雨或毛毛雨，这与T. Yoshimura[10]对日本Aratsu桥施工过程中观测到的斜拉索风雨振现象一致。风雨振与降雨大小无明显关系，这可能是因为采集的样本少，或者是雨量计算的方法不同，未反应振动的真实情况。

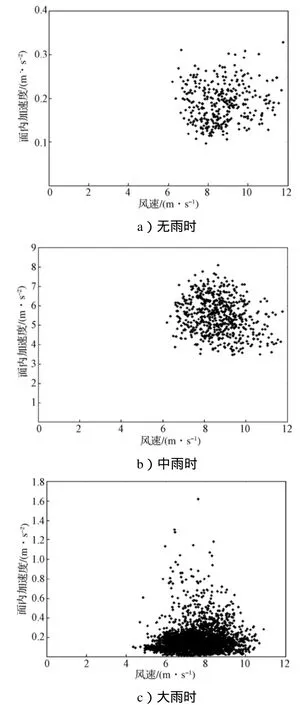
图9 S20索振幅与风速的关系Fig.9 Vibration amplitude of cable S20 vs wind speed

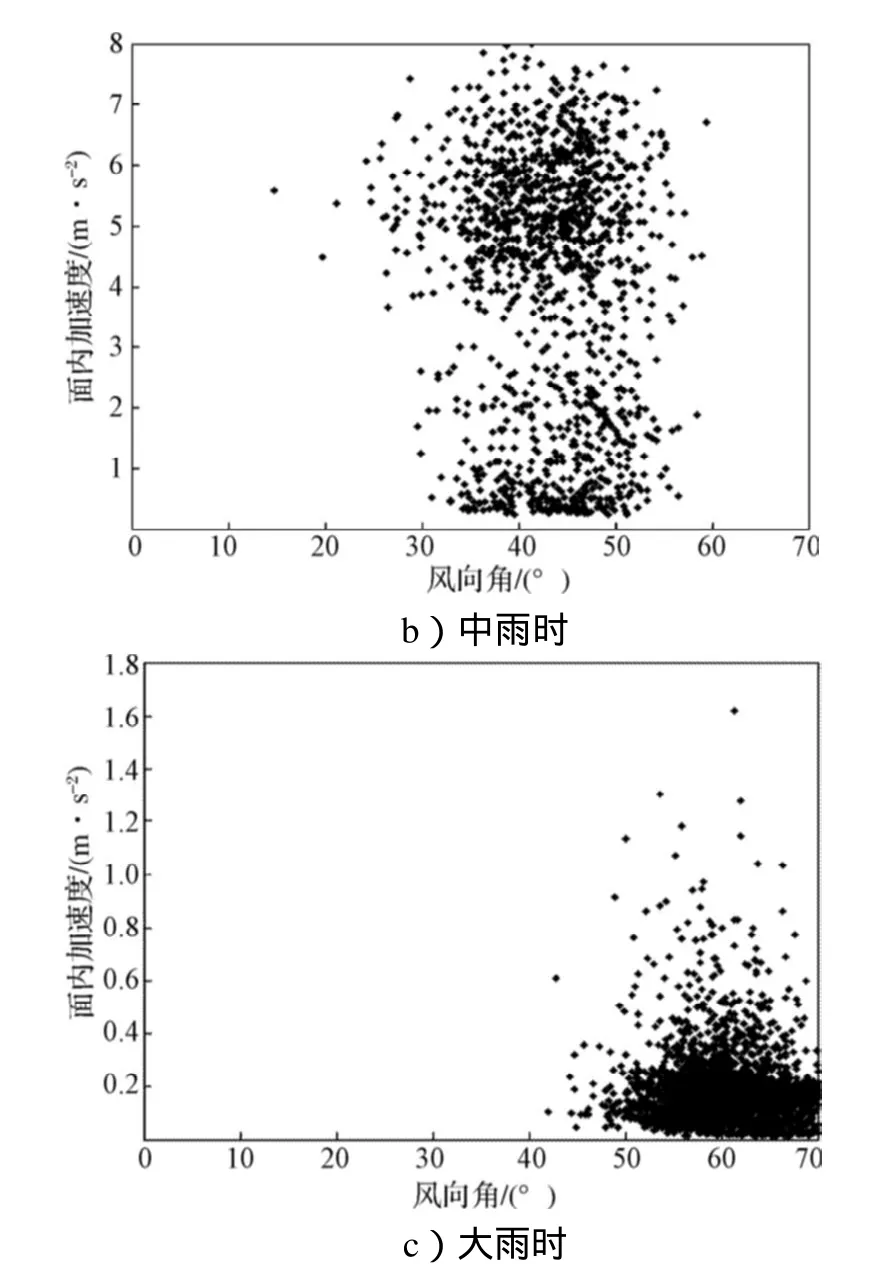
图10 S20索振幅与风向角的关系Fig.10 Vibration amplitude of cable S20 vs wind yawing angle

3 气动负阻尼比、风场参数与风雨振各阶段的关系

对采集的S20索的风雨振信号进行频谱分析与滤波处理，图11为S20索滤波前、后风雨振时程图与频谱图。从图可以看出，在图示时间段内发生了多次风雨振，从起振到衰减，吸收能量再起振，滤波后频谱为2.58Hz（相当于第四阶模态频率）。

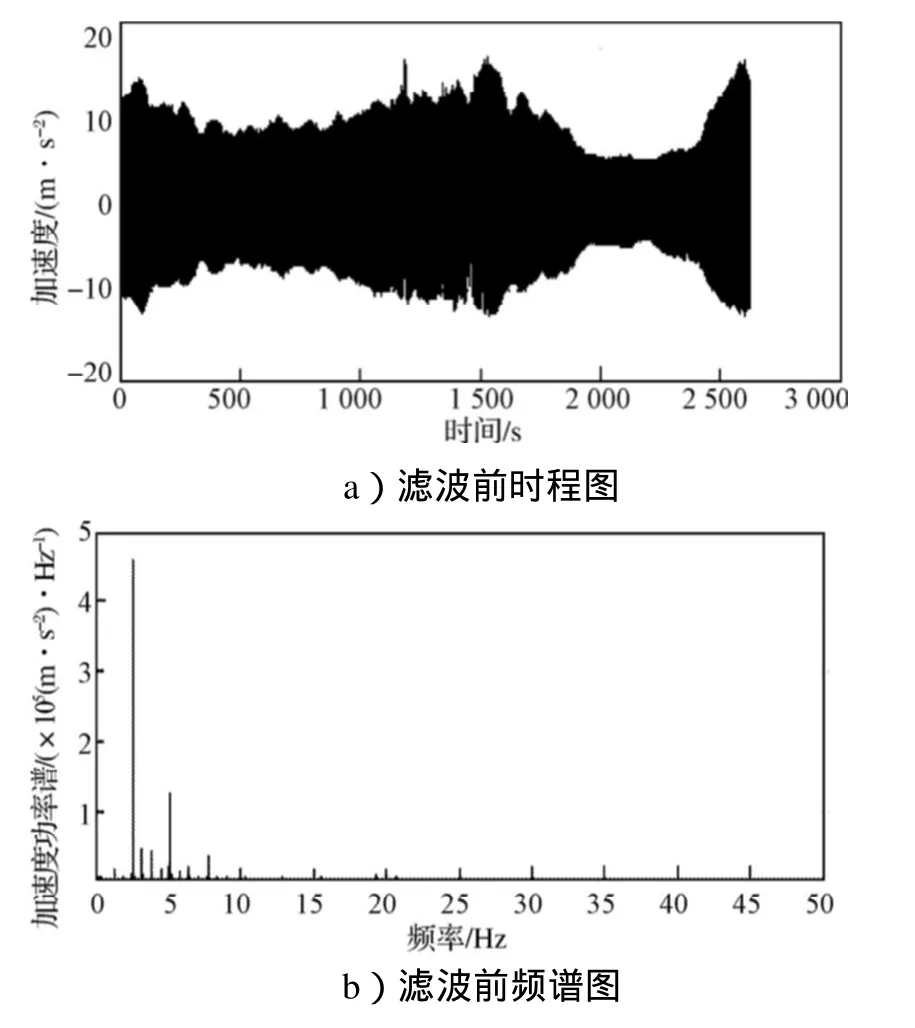
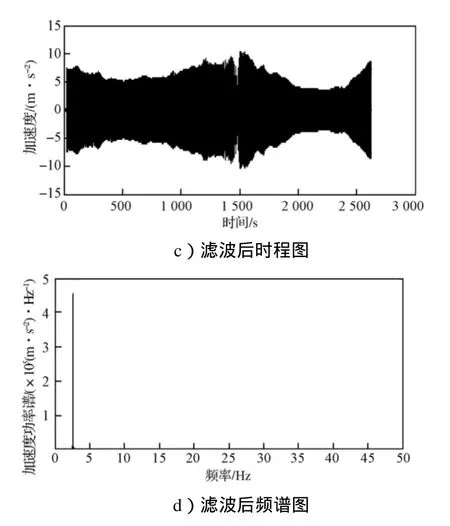
图11 S20拉索风雨振时程图及频谱图Fig.11 Schedule plan and the spectrum for cable S20 in wind-rain induced vibration

采用最小二乘法对滤波后的风雨振加速度时程图进行拟合，拟合结果如图12所示。从拟合结果可知，有以下几个阶段：0～500s为振幅衰减过程，气动负阻尼比为-0.0297%；500～1500s为风雨振过程，气动负阻尼比为-0.0406%；1500～2000s为衰减过程，气动负阻尼比为-0.0244%；2000～2200s为能量吸收阶段；2200～2500s为风雨振过程，气动负阻尼比为-0.0505%。

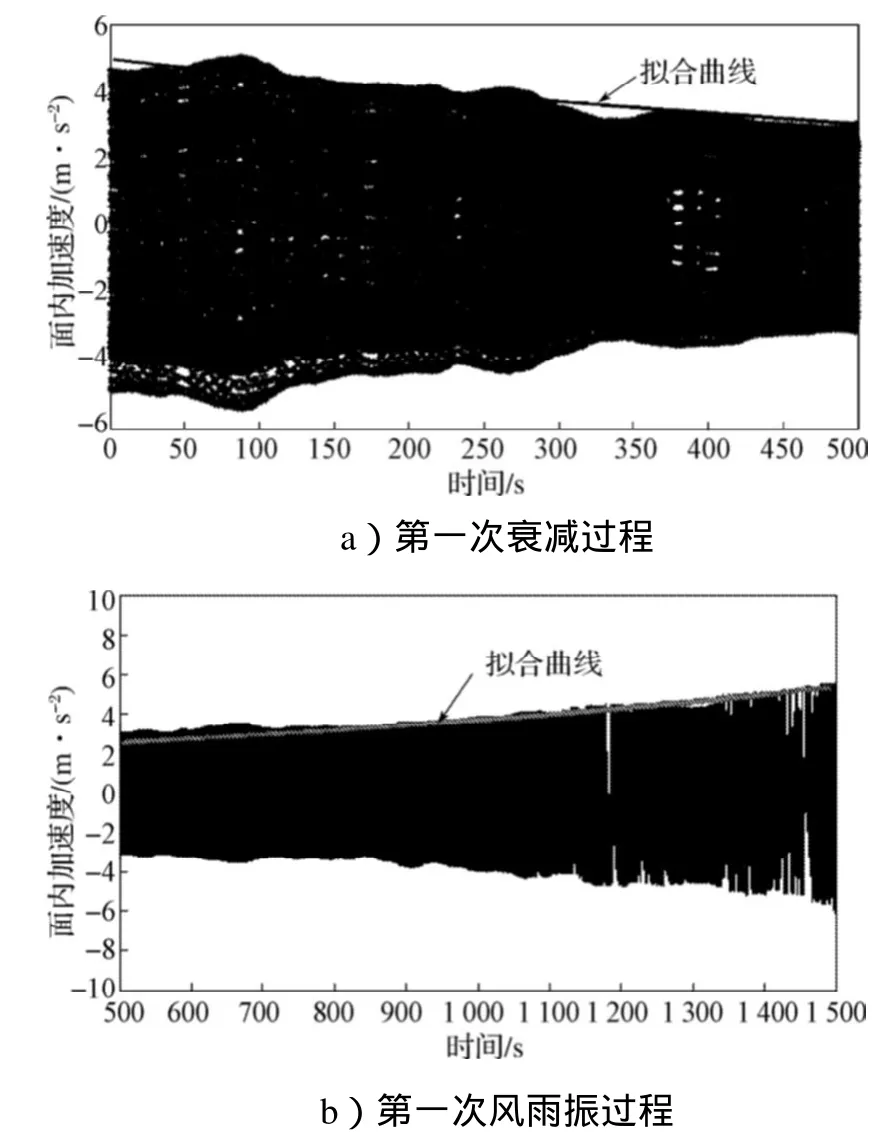
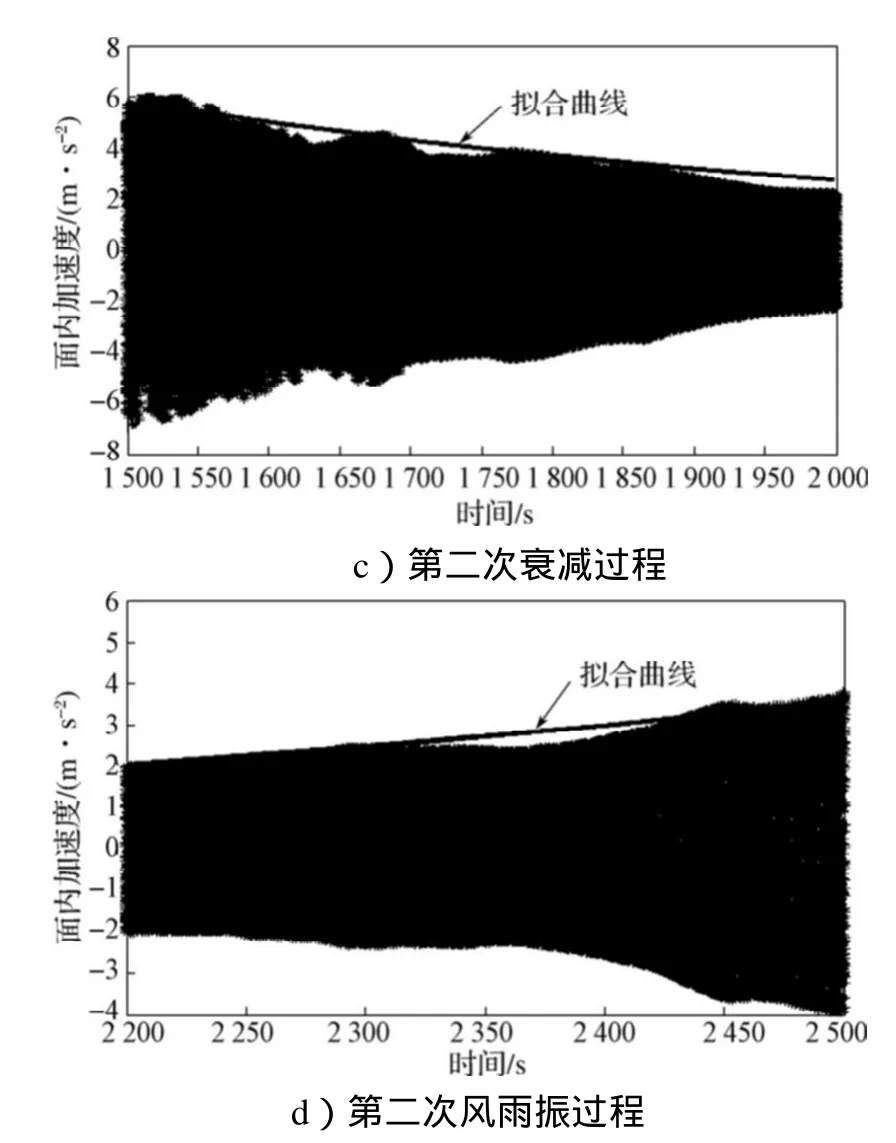
图12 拟合加速度时程图Fig.12 Schedule plan for fitting acceleration

S20拉索风雨振过程中，气动负阻尼比与风场参数变化曲线见图13。在500～1500s与2200～2500s发生了风雨振现象，最大的振幅分别为6.250m/s2和3.735m/s2，而气动负阻尼比分别为-0.0406%和-0.0505%，这表明气动负阻尼比绝对值的大小与最大振幅的大小没有必然的联系。气动负阻尼比的绝对值越大，只是表明拉索振幅的变化越大，瞬间大幅振动，对拉索的正常使用构成威胁。0～500s与1500～2000s的气动负阻尼比分别为-0.0297%和-0.0244%，其值相对较小且绝对值小于拉索的第四阶等效模态阻尼比，振幅逐渐减少。从理论上讲，当风雨引起的气动负阻尼比的绝对值小于结构阻尼比时，风雨振将不会发生，这与试验结果相符。

比较图13a与图13b可知，发生风雨振的时间段，气动负阻尼比对风速的变化相当敏感。风速变化趋势为上升，气动负阻尼比就增加；风速变小，气动负阻尼比随之变小。只有当风速达到某一值时，才会发生风雨振，这与理论相符。

风雨振过程中，在500～1500s和2200～2500s时风向角平均值分别为53.85°和38.68°（图13c），这符合发生风雨振的条件。风向角的改变影响气动负阻尼比，两者之间的耦合关系，有待进一步研究。

从图13d可以看出，在考察风雨振的整个过程中都是中雨，大小几乎没变化，这有利于上水线的形成。综上所述只有影响因素都达到风雨振产生的条件，才形成风雨振。

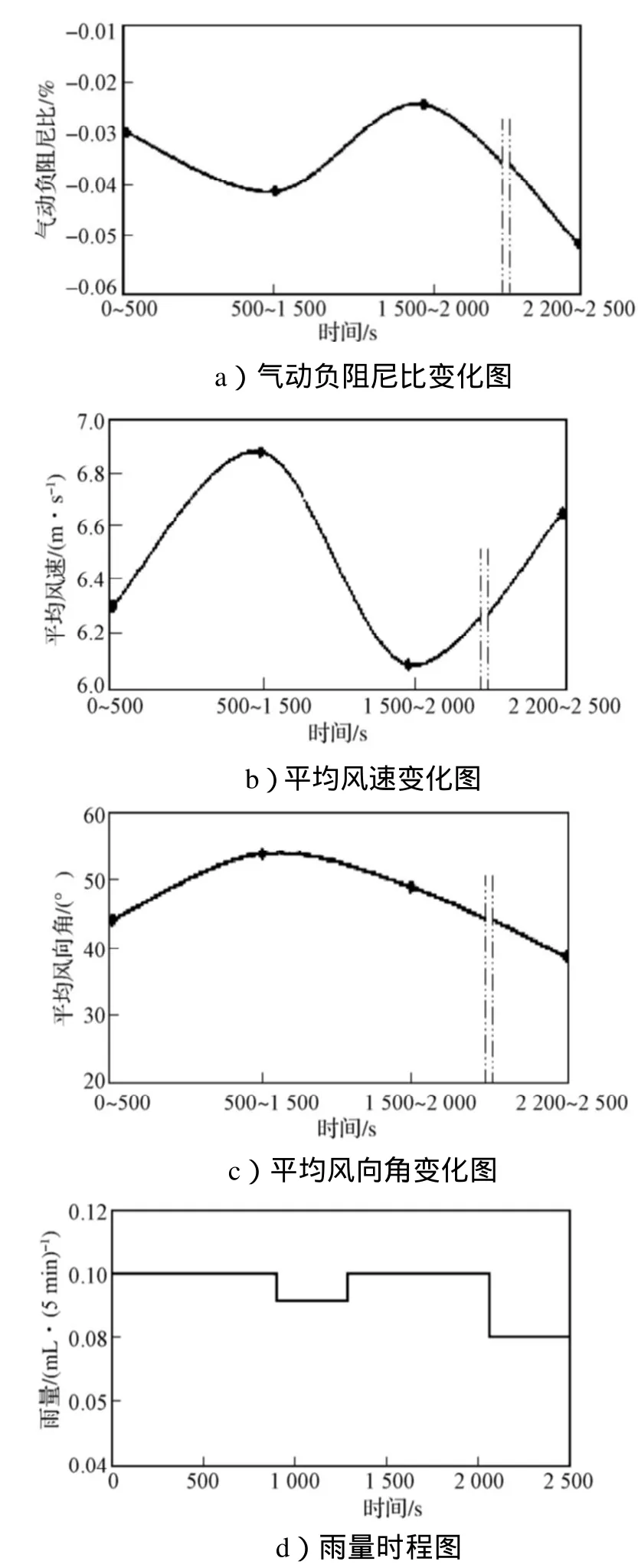
图13 S20拉索风雨振中气动负阻尼比与风场参数变化图Fig.13 The wind parameters and aerodynamic negative damping ration for cable S20 in wind-rain induced vibration

本文以洞庭湖大桥拉索风雨振现场观测试验的数据为依据，对风雨振的主要影响因素做了定性和定量的分析，降低气动负阻尼比是抑制拉索风雨振的关键。

[1]Hikami Y，Shiraishi N. Rain-Wind Induced Vibrations of Cables Stayed Bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics，1988，29(1/2/3)：409-418.

[2] 陈政清，柳成荫，倪一清，等. 洞庭湖大桥拉索风雨振中的风场参数[J]. 铁道科学与工程学报，2004，1(1)：52-57.Chen Zhengqing，Liu Chengyin，Ni Yiqing，et al. Wind Parameters in Wind-Rain Induced Stay Cable Vibration on Dongting Lake Bridge[J]. Journal of Railway Science and Engineering，2004，1(1)：52-57.

[3] 柳成荫，陈政清，倪一清，等. 洞庭湖大桥风雨振现场观测实验研究[C]//第十一届全国结构风工程学术会议论文集. 三亚：[出版者不详]，2004：477-482.Liu Chengyin，Chen Zhengqing，Ni Yiqing，et al.Experimental Research of Field Measurements of Wind-Rain Induced Cable Vibration on Dongting Lake Bridge[C]//Proc 11th National Conf Structure and Wind Eng.. Sanya：[s. n. ]，2004：477-482.

[4] 李文勃，林志兴. 抑制斜拉桥拉索风雨激振的气动措施研究[J]. 土木工程学报，2005，38(5)：48-53.Li Wenbo，Lin Zhixing. A Study on Aerodynamic Control Countermeasures to Rain-Wind Induced Vibration of Cables in Cable-Stayed Bridge[J]. China Civil Engineering Journal，2005，38(5)：48-53.

[5] 王修勇，陈政清，倪一清，等. 斜拉桥拉索磁流变阻尼器减振技术研究[J]. 中国公路学报，2003，16(2)：52-56.Wang Xiuyong，Chen Zhengqing，Ni Yiqing，et al. Study of Mitigating Cables Vibration on the Cable-Stayed Bridges Using Magnetorheological(MR) Dampers[J]. China Journal of Highway and Transport，2003，16(2)：52-56.

[6]Chen Z Q，Wang X Y，Ko J M，et al．MR Damping System for Mitigating Wind-Rain Induced Vibration on Dongting Lake Cable-Stayed Bridge[J]. Wind and Structures，2004，7(5)：293-304.

[7] 项海帆. 公路桥梁抗风设计指南[M]. 北京：人民交通出版社，1996：30-32.Xiang Haifan. Anti-Wind Design Guide for Road Bridge[M]. Beijing：People's Communications Press，1996：30-32.

[8]Vandiver J K，Dunwoody A B，Campbell R B，et al. A Mathematical Basis for the Random Decrement Vibration Signature Analysis Technique[J]. Journal of Mechanical Design，1982, 104：307-313.

[9] 王修勇，陈政清，何旭辉，等. 洞庭湖大桥风雨振减振试验研究[J]. 桥梁建设，2002(2)：11-14.Wang Xiuyong，Chen Zhengqing，He Xuhui，et al.Research of Wind-Rain Induced Vibration and Mitigating on Dongting Lake Bridge[J]. Bridge Construction， 2002(2)：11-14.

[10]Yoshimura T. Aerodynamic Stability of Four Medium Span Bridge Kyushu District[J]. Journal of Wind Engineering and Industrial Aerodynamics，1992，42(1/2/3)： 1203-1214.