编码辅助信噪比估计算法的性能分析

杨晓宇，陈鸿昶，克 兢，韩 博

（1.解放军信息工程大学，河南郑州 450002;2.空军工程大学信息与导航学院，陕西西安 710077）

编码辅助信噪比估计算法的性能分析

杨晓宇1，陈鸿昶1，克 兢2，韩 博2

（1.解放军信息工程大学，河南郑州 450002;2.空军工程大学信息与导航学院，陕西西安 710077）

研究了基于编码辅助的信噪比期望最大（EM）估计算法。在分析编码辅助算法模型的基础上，建立了无编码辅助算法与编码辅助算法的联系，将无编码辅助算法看作是编码辅助算法的一种特殊情况。此外，将同步估计中的嵌入估计算法运用到信噪比迭代估计中，得到了一种简化的编码辅助算法，克服了原算法计算量过大的缺点。仿真结果表明，简化后的算法在降低算法复杂度的同时，仍能保持原算法的估计性能。

信噪比估计;编码辅助;期望最大算法

许多现代无线通信系统都依赖于信噪比的精确估计以获得最佳的性能。近年来，有许多文献对信噪比估计算法进行了研究。根据信噪比估计过程中是否有信道译码器的参与，信噪比估计算法可分为无编码辅助（Non－Code－Aided，NCA）［1］和编码辅助（Code－Aided，CA）［2］。传统的信噪比估计算法主要是无编码辅助算法，一般采用最大似然（ML）算法推导出信噪比的估值，然而在一些情况下，ML的解析值并不易求得［3］。文献［4］提出了一种基于期望最大（EM）算法的信噪比估计算法，该算法采用迭代的方式逐步逼近信噪比的ML估计值，在中高信噪比下性能良好。随着Turbo码和LDPC码等高效编码技术在低信噪比条件下的广泛应用，无编码辅助算法由于假定所有发送符号的概率相同而不考虑信道编码提供的信息，即认为接收符号的先验信息为零，因而在低信噪比情况下不能很好的工作［5］。为此，文献［2］提出了一种基于编码辅助的信噪比EM迭代估计算法，其基本思想是将信噪比估计算法与LDPC码的迭代译码过程相结合，利用译码器提供的软信息得到接收符号的先验信息，从而提高了低信噪比下的估计精确度，然而该算法复杂度较高，使用的范围受到了很大的限制。

本文在文献［2］的基础上进行了改进，通过引入嵌入估计算法对原算法进行了简化，从而减小了计算复杂度。此外，通过分析算法模型，本文还建立了无编码辅助算法与编码辅助算法的联系，将无编码辅助算法看作是编码辅助算法的一种特殊情况。

1 基于编码辅助的信噪比估计算法

考虑LDPC编码后的信号通过高斯白噪声信道（AWGN）到达接收机，假设已具备了良好的同步，则接收到的基带等效信号可以表示为

式中:rk是匹配滤波器输出的采样;A是信道增益;sk是编码调制后的符号，sk∈Q，Q是调制的星座点集合;nk为零均值的高斯白噪声，噪声方差为σ2。根据信噪比的定义，接收信号的信噪比可表示为γ=A2/σ2。

传统方法采用ML准则直接计算信噪比，由于需要遍历发送符号的所有排列，运算量随着符号个数的增加而呈指数式增长，实际中很难进行处理。当待估参数不容易处理，或无法得到ML估计值的解析式时，EM算法［6］通过假设一些“潜在数据”扩充到原始观察数据中，组成“完全数据集”，然后采用迭代的方式逐步逼近ML估计值。文献［2］提出以EM算法来迭代计算编码辅助下的信噪比ML估计值。

定义θ=［A，σ2］T为待估计的参数矢量，r为rk的矢量表示，S=（s0，s1…，sk－1）∈Ak，定义 Z=［rT，sT］T为“完全数据集”，则编码辅助的信噪比EM迭代算法可表示为

式中:Re{·}表示取实部;*表示复数共轭;ηk和ρk分别定义为信道编码符号sk在条件^θ（i－1）下的后验均值和后验均方值，即

2 算法改进

2.1 信噪比估计算法的一般表述

本节考虑将式（2）表述的编码辅助信噪比EM迭代算法作为信噪比EM迭代估计算法的一般表述，也就是说，将非编码辅助的方法作为一个特例纳入到编码辅助方法体系中。

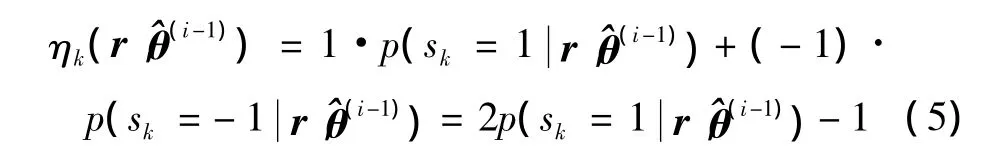
1）非编码辅助算法

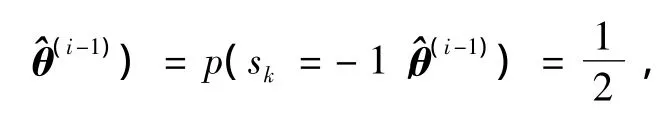
将式（7）代入式（2），即可进行非编码辅助的迭代运算，其中信道增益和噪声方差的初始值可以设为A（0）=∞，（σ（0））2=1。

2）编码辅助算法

编码辅助方法充分利用信道编码的结构特性，将迭代译码的软输出信息作为数据符号的先验信息。对于以最大后验概率（MAP）译码的LDPC迭代译码器，编码辅助算法认为APPs的值可以由一定次数迭代后的译码器以对数似然函数（LAPPR）的形式提供。BPSK调制下ηk的计算与文献［2］类似，此时LAPPR定义为

将式（6）代入式（5），可得

需要指出的是，在LDPC软判决迭代译码算法前，译码器需要估计信噪比（或噪声功率σ2）的值以初始化置信传播（BP）译码［7］，在二进制加性高斯白噪声信道下（BI－AWGN），初始化由式（10）完成

编码辅助的方法可以首先采用非编码辅助方法估计出信噪比的初值，代入式（10）初始化LDPC译码器，然后进行信噪比的迭代估计。

通过上述推导，将编码辅助和非编码辅助的方法进行统一，两者的区别仅在于取不同的ηk值，即

2.2 一种低复杂度的编码辅助信噪比估计算法

实际应用中，考虑到芯片的处理能力和系统的实时性要求，应尽量减少算法的运算量。文献［2］提出的编码辅助算法在低信噪比下仍具有较好的性能，但其主要的缺点在于算法复杂度较大［8］，这是由于该算法要求在每次EM迭代中，译码器都需要经过多次迭代直至得到一个稳态的LAPPR值，作为APPs的近似。这一问题也存在于基于编码辅助的同步EM估计算法中，对此，文献［9］提出了一种嵌入估计算法，将EM迭代与Turbo译码迭代相结合，从而降低了同步估计的计算复杂度。本文将这种嵌入算法引入到LDPC编码辅助的信噪比估计方法中，在每次EM迭代中只进行1次LDPC译码迭代，并且将本次迭代后译码器的状态信息保存给下一次迭代过程。图1给出了该算法的框图。

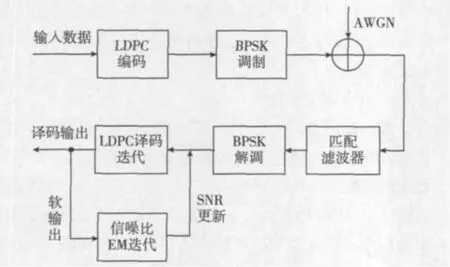
图1 本文算法框图

需要指出的是，在这种嵌入式迭代技术的每次EM迭代中，Turbo译码器不需要多次迭代直至稳态，而只进行1次译码迭代，此时，译码器输出的软信息对APPs的近似效果不如多次译码迭代的好，因而可能造成同步估计性能的下降［10］。然而，该技术对LDPC编码辅助的信噪比估计算法的性能并不会有太大影响，这是由于LDPC译码和EM估计算法以相互补充的方式进行工作:EM估计算法利用LDPC译码器提供的APPs的近似值计算出信噪比估值后，这一信噪比又送入LDPC译码器以计算出更精确的APPs近似值。

3 仿真结果与性能分析

本节使用蒙特卡洛方法对提出的编码辅助信噪比估计改进算法进行仿真以验证其有效性。仿真条件:AWGN信道;调制方式为BPSK;信道编码采用码率R=0.5的LDPC码，码长2 000;EM迭代次数为10;蒙特卡洛仿真次数为500。

实验表明，对于CA算法，信噪比初值通过采用NCA方法得到或随机选取对最后估计结果并无影响。简单起见，CA算法仿真中信噪比的初值均设为10 dB。

对于多次仿真，信噪比的估计值^γ是一个随机变量，可以采用均方误差（MSE）来衡量估计算法的性能，即

式中:γ为AWGN信道的真实信噪比。实际应用中，采用估计样本的算术平均近似式（12）的统计平均，可得

式中:N为蒙特卡洛仿真实验次数;^γt（t=1，2，…，N）表示第t次仿真实验的信噪比估计值。

图2对非编码辅助算法（NCA）、原编码辅助算法（原CA）［2］和本文提出的改进编码辅助算法（改进CA）得到的估计信噪比均值与真实值进行了比较。如图2所示，对于NCA，当信噪比较大时（如SNR＞0 dB），信道噪声估计平均值曲线与真实值曲线相重叠，表示估计准确;而当信噪比增大时，估计出现了偏差。对于原CA和改进CA，在整个仿真信噪比范围内，估计都准确。

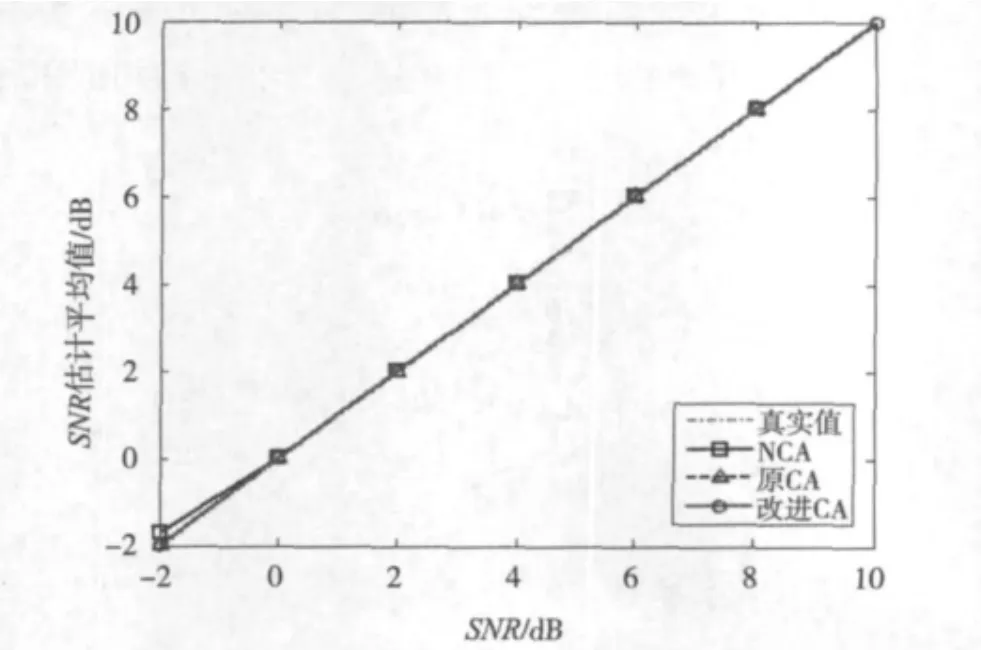
图2 不同算法下SNR估计的均值图

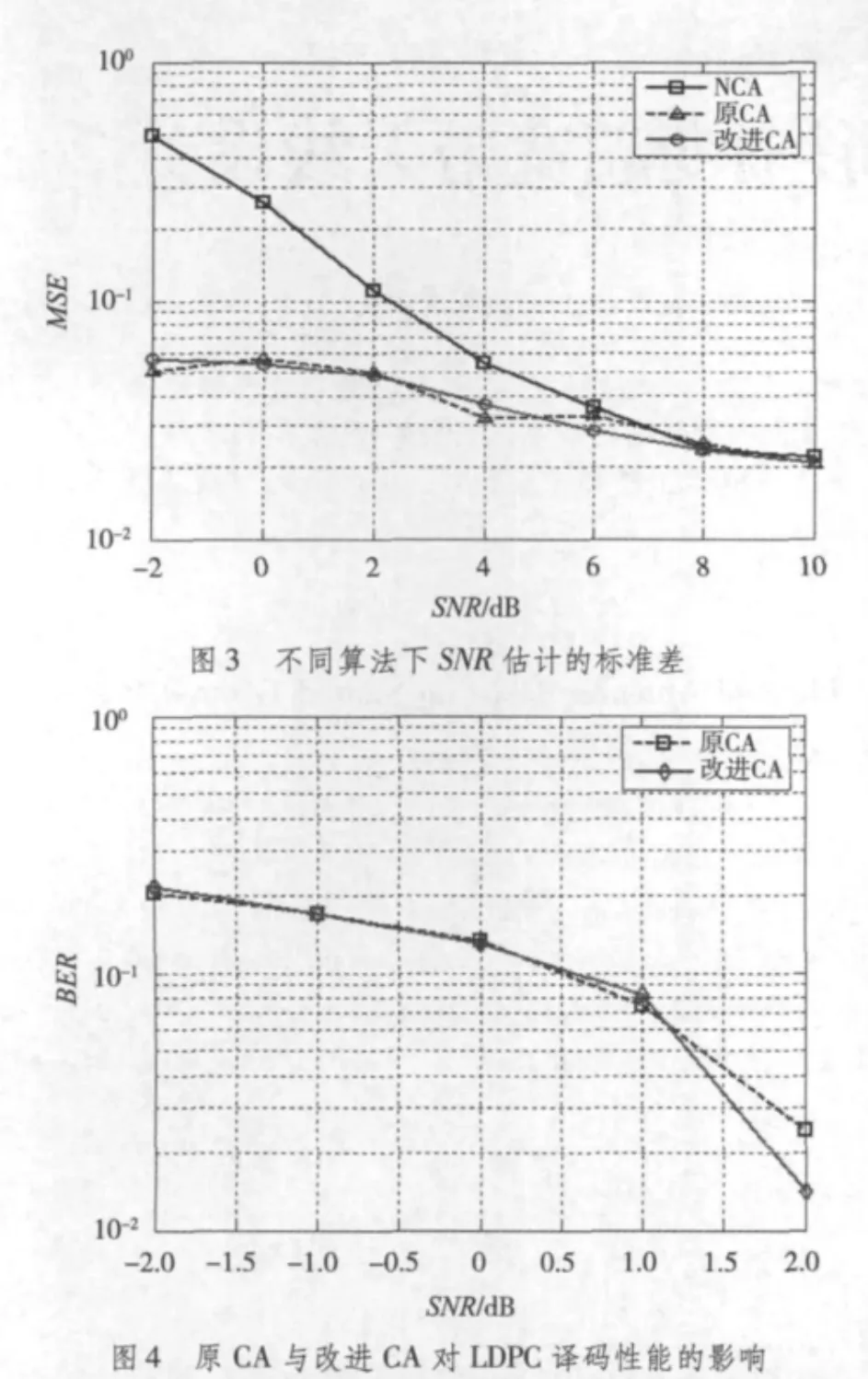
同样的结论也可通过比较3种算法信噪比估计的MSE得到。如图3所示，在信噪比较低时，原CA和改进CA估计性能要明显优于NCA，这是由于非编码辅助假定所有发送符号等概率，而编码辅助算法利用LDPC译码器得到了更准确的数据信息。值得注意的是，当信噪比增加到一定值时（例如SNR＞6 dB），3种算法的性能基本相似，这是由于此时噪声的影响已经变得很小，主要是对有用信号进行操作。仿真结果还表明，改进CA与原CA在整个信噪比取值范围内估计性能非常接近。

图4给出了两种编码辅助算法的误码率（BER）曲线，其结论与前述一致，即改进的CA在计算复杂度降低的同时保持了原CA的性能。

如前所述，改进CA和原CA在计算复杂度上的区别取决于每次EM迭代内的LDPC译码迭代次数。为了衡量译码过程的计算量，在MATLAB环境下，使用Intel Core 2 Duo CPU 2.93 GHz的计算机运行该程序，采用平均CPU运行时间作为计算复杂度的衡量标准。表1分别给出了1次EM迭代中1次LDPC译码迭代和1次EM迭代中5次LDPC所用的CPU时间。从表中可以看出，算法的运算量主要集中在LDPC迭代译码的计算上，在1次EM迭代中，LDPC迭代占用98% ～99%的时间，与原CA在1次EM迭代中进行5次LDPC迭代相比，改进CA在1次EM迭代中只进行1次LDPC迭代，从而将运行时间减少了63%。

表1 平均CPU时间比较

4 结论

本文研究了编码辅助的信噪比EM迭代估计方法。通过分析该算法模型，将该模型推广到非编码辅助信噪比估计算法，提出将非编码辅助的信噪比EM迭代算法作为一个特例纳入到编码辅助方法中。编码辅助算法在每次信噪比EM迭代估计中需要进行多次LDPC译码迭代，运算量较大，影响了其实用性，对此，本文利用信噪比估计与LDPC译码间相互补充的工作过程，通过引入嵌入估计算法对其进行简化，改进后的算法复杂度低，并且能够保持原算法的估计性能。

:

［1］BRANNSTROM F，RASMUSSEN L K.Non－data－aided parameter estimation in an additive white gaussian noise channel［C］//Proc.IEEE International Conference Symposium on Information Theory.［S.l.］:IEEE Press，2005:1446－1450.

［2］WU N，WANG H，KUANG J M.Code－aided SNR estimation based on expectation maximisation algorithm［J］.Electronics Letters，2008，44（15）:924－925.

［3］GAPPMAIR W，LOPEZ－VALCARCE R，MOSQUERA C.ML and EM algorithm for non－data－aided SNR estimation of linearly modulated signals［C］//Proc.6th International Symposium on Communication Systems，Networks and Digital Signal Processing，2008.Graz:IEEE Press，2008:530－534.

［4］WIESEL A，GOLDBERG J，MESSER H.Non－data－aided signal－tonoise estimation［C］//Proc.IEEE International Conference on Communications，2002.New York:IEEE Press，2002:197－201.

［5］DANGL M A，LINDNER J.How to use a priori information of data symbols for SNR estimation［J］.IEEE Signal Processing Letters，2006，13（11）:661－664.

［6］DEMPSTER A P，LAIRD N M，RUBIN D B.Maximum likelihood from incomplete data via the EM algorithm［J］.Journal of the Royal Statistical Society，Series B（Methodological），1977，39（1）:1－38.

［7］MACKAY D J C.Good error correcting codes based on very sparse matrices［J］.IEEE Trans.Information Theory，1999，45（2）:399－431.

［8］包建荣，詹亚峰，殷柳国，等.低SNR下基于LDPC译码的迭代SNR估计［J］.通信技术，2012，43（1）:1－6.

［9］HERZET C，WYMEERSCH H，MOENECLAEY M，et al.On maximumlikelihood timing synchronization［J］.IEEE Trans.Communicaitons，2007，55（6）:1116－1119.

［10］NOELS N，HERZET C，DEJONGHE A，et al.Turbo synchronization:an EM algorithm interpretation［C］//Proc.IEEE International Conference on Communicaitons，2003.［S.l.］:IEEE Press，2003:2933－2937.

Performance Analysis of Code－aided SNR Estimation

YANG Xiaoyu1，CHEN Hongchang1，KE Jing2，HAN Bo2

（1.PLA Information Engineering University，Zhengzhou 450002，China;2.Information and Navigation Institute，Air Force Engineering Unversitg of PLA，Xi’an 710077，China）

The expectation－maximization（EM）estimation of signal－to－noise ratio（SNR）for coded transmission systems is researched.By studying the model of code－aided（CA）estimation，a connection of the CA algorithm with the conventional non－code－aided（NCA）estimators is made.Therefore，the CA estimator can be used to implement the NCA estimation.Further，a simplified version of the code－aided（CA）estimation algorithm is proposed by introducing the embedded estimation technique to reduce the computational complexity related to the iterative process of the estimator.The performance of the improved CA approach is shown to be close to the original CA at considerably reduced complexity.

SNR estimation;code－aided;EM algorithm

TN911.23

A

【本文献信息】杨晓宇，陈鸿昶，克兢，等.编码辅助信噪比估计算法的性能分析［J］.电视技术，2013，37（3）.

国家自然科学基金项目（61001111）

杨晓宇（1984— ），女，硕士生，主研通信信号处理;

陈鸿昶（1968— ），教授，主研计算机应用于信息处理;

韩 博（1987— ），硕士生，主研通信信号处理技术。

责任编辑:薛 京

2012－07－25